QPR-NN:一种结合二次多项式回归与神经网络的推荐算法
2019-09-10廖彬张陶于炯国冰磊李敏刘炎
廖彬,张陶,于炯,国冰磊,李敏,刘炎
(1.新疆财经大学丝路经济与管理研究院,830012,乌鲁木齐;2.新疆财经大学统计与数据科学学院,830012,乌鲁木齐;3.新疆大学信息科学与工程学院,830012,乌鲁木齐;4.新疆医科大学医学工程技术学院,830012,乌鲁木齐;5.清华大学软件学院,100084,北京)
据文献[1]统计,2017年全球数据总量为21.6 ZB,按照每年40%左右的增长率计算,预计到2020年全球的数据总量将达到40 ZB,如何更好地管理并利用这些海量数据,是大数据研究的核心内容。特别是在互联网领域,面对规模庞大的数据,如何进行精准地选择成为困扰用户的一大难题。推荐系统为了解决这个问题,一方面从用户的角度出发,高效地从海量数据中选择出用户可能感兴趣的物品(如:电影、书籍、音乐、商品、新闻、微博等);另一方面从商家的角度出发,向用户提供更为个性化的服务,提高用户的黏性及信任度,从而提高经济收益。
根据数据源的不同,当前主流的推荐系统所采用的核心算法主要分为基于人口统计学的推荐[2]、基于内容的推荐[3]以及基于协同过滤的推荐[4-5]这3种。协同过滤算法在早期取得了不错的应用效果,但是随着数据量以指数级增加,数据稀疏性、冷启动以及算法的可扩展性等问题不断出现。因此,研究能同时适应数据高规模及高稀疏性特点的推荐算法成为了当前的研究热点。
近年来,深度学习研究得益于海量数据的积累、硬件计算能力的提升以及算法研究者的努力而不断发展,特别是深度神经网络[6]及其变种形式的卷积神经网络[7]、循环神经网络[8]等,在机器视觉、自然语言处理等领域大放异彩。深度学习的本质是对数据特征进行深层次地抽象挖掘,通过大规模数据来学习有效的特征表示以及复杂的映射机制,从而建立起数据模型。深度学习作为一种适应度较高的数据建模方法,理论上可以广泛地应用到不同的领域,其中就包括推荐系统。但是,目前深度学习应用到推荐系统的工作相对较少。
为了解决现有推荐算法不能很好适应数据高规模及高稀疏性的现状,本文结合深度学习建模方法通用性的特点,提出一种结合二次多项式回归与神经网络(QPR-NN)的推荐算法。QPR-NN首先利用QPR模型来对用户对物品的评分数据进行特征提取及降维,经过QPR模型处理后的数据作为深度学习训练模型的输入,训练后的模型用于预测用户对物品的评分。与主流推荐算法进行的平分绝对误差EMA以及均方根误差ERMS这2个评价指标的对比实验表明,QPR-NN算法能够有效地提高推荐质量。
1 相关工作
由于本文的关注点是利用二次多项式回归及深度学习算法来解决现有推荐算法不能很好地适应数据高规模及高稀疏性的问题,所以本节首先对该问题的已有相关研究进行阐述,其次对深度学习在推荐系统上的应用研究进行介绍。
1.1 解决数据高规模及高稀疏性问题的研究
随着分布式计算模型MapReduce的普及,推荐算法逐渐从单机向分布式模式发展,进而很好地解决了数据的高规模问题。Guo等和Zhao等将协同过滤算法移植到Hadoop平台,提高了算法的并行计算能力[9-10]。Schelter等面对用户数据量快速增长的问题,提出了基于MapReduce的近邻协同过滤算法,并通过Yahoo的7亿条音乐数据证明了算法在效率上的明显提升[11]。廖彬等对MapReduce架构下的协同过滤算法存在的性能问题进行了分析,并提出利用Spark内存计算[12]、相似度计算效率优化[13]、Spark DAG调度[14]等方法来进一步提高分布式推荐算法的执行效率。
针对高稀疏性问题,一般采用数据填充、聚类、矩阵分解等方法解决。数据填充是在进行相似性计算之前,对用户及评分矩阵数据进行填充,从而降低其稀疏性。聚类是一种有效的数据降维方法,能够在有效地降低算法计算量的同时提高推荐质量。矩阵分解中最具有代表性的工作是奇异值分解(SVD)[15-16],文献[17]提出了带正则化的基于迭代最小二乘法的矩阵分解方法,文献[18]通过矩阵分解实现对原始数据的降维及数据填充,并引入了时间衰减函数预处理用户评分,提升了推荐算法的准确度。
1.2 深度学习在推荐算法上的应用研究
Salakhutdinov等最早在NIPS 2007上提出了使用限制玻尔兹曼机进行评分预测,该模型是2层的类二部图结构,通过非线性关系关联隐含层与可见层的数据信息,但该模型最大的问题是链接隐含层与评分层的权重参数(矩阵)规模太大[19]。在后期工作中,部分工作利用深度神经网络模型来作为信息变换模型,例如:文献[20]使用多层降噪自动编码机将文本特征与评分预测特征相融合;文献[21]利用卷积神经网络解决音乐推荐系统中的冷启动问题。除此之外:文献[22]将卷积神经网络与协同过滤算法进行结合,提高了音乐推荐的质量;微软公司提出了深度结构化语义模型(DSSM),该模型是基于多层神经网络模型搭建的广义语义匹配模型,通过级联的深度神经网络模型的映射与变换,最终在同一个隐含空间内表示了推荐系统中的用户和物品,并可以使用余弦相似度进行计算[23];文献[24]使用循环神经网络进行基于session的推荐,充分考虑了物品的时序关系;Brebisson等使用神经网络模型解决ECML/PKDD会议的数据挑战题目“出租车下一地点预测”,取得了比赛第一名的成绩,并且对多种多层感知器模型以及循环神经网络模型进行了对比,发现基于改进后的多层感知器模型会取得最好的效果[25]。
已有工作大部分是利用深度学习算法作为训练模型去处理推荐系统的数据,而在输入数据的特征提取方面,往往采用传统的几种处理方法(如RaF[26]、SVD[15-16]及PMF[27-28]等),并没有更多地考虑到用户和物品之间的适配度。本文与已有工作的最大不同之处在于:在分析已有特征提取方法缺陷的基础上,为了更好地挖掘用户与物品之间的相关性,提出QPR模型对数据进行特征提取及降维,然后将处理后的数据作为深度学习训练模型的输入,最后将训练后得到的模型用于推荐系统的评分预测,提高了算法的推荐质量。
2 基于QPR模型的特征表示模型
2.1 已有特征表示模型的优缺点分析
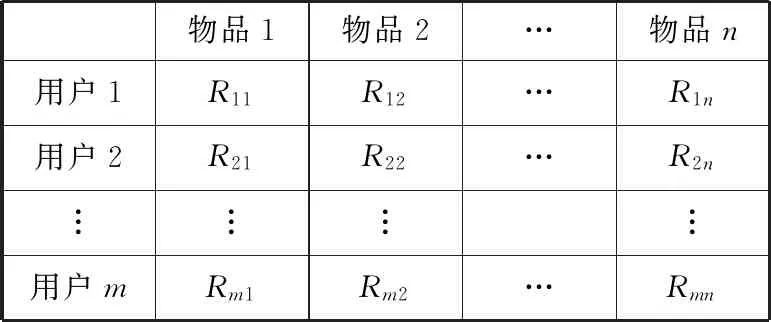
若用m表示用户数量、n表示物品数量,协同过滤推荐算法的输入可以表示为m×n的用户项目评分矩阵R,具体如图1所示,其中Rij表示第i个用户对第j个物品的评分,Rij∈Rm×n,i∈[1,m],j∈[1,n]。Rij的取值范围可以根据实际应用系统的特点进行设定,连续或离散的情况都有,大多数应用系统采用数值为1~5的离散值来表示评分,而Rij=0则表示用户尚未对该项目进行评分。
物品1物品2…物品n用户1R11R12…R1n用户2R21R22…R2n︙︙︙︙用户mRm1Rm2…Rmn
图1 用户项目评分矩阵R
本文需要使用用户项目评分矩阵R获得用户及项目的特征表示,目前主流的特征表示方法有RaF、SVD及PMF,这3种方法的原理及优缺点分析如表1所示。

表1 几种特征表示方法的对比分析
2.2 利用QPR模型提取用户和物品的特征
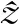
(1)
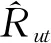
(2)
为了简化式(2),设
(3)
(4)
将式(3)与式(4)代入式(2),可以得到
(5)
可以看出,式(5)中的eu与ft分别与其对应的用户u与物品t相关。使用最小二乘损失函数,可以得到模型的拟合误差Q为
(6)
展开式(6),得到
(7)
当式(7)达到最优最小值解时,即计算出了所需的用户特征矩阵U与物品特征矩阵T。
3 QPR-NN算法
3.1 QPR与NN模型的连接
在2.2节得到用户特征矩阵U与物品特征矩阵T的基础上,本节探讨怎样利用神经网络模型,对这些输入数据进行训练,并利用训练后的模型拟合评分数据,从而实现推荐功能。
(1)神经网络输入层。设输入向量为v0,v0由用户特征Ui与物品特征Tj通过链接函数fc(神经网络中采用concatenate函数)链接而成,公式为
v0=fc(Ui,Tj)
(8)
(2)隐藏层。输入向量v0经过第1层隐藏层后,需要引入一些非线性特性,此时需要使用激活函数fc(神经网络中采用activation函数)进行激活,公式为
v1=fa(w1v0+b1)
(9)
式中:v1为输出向量;w1为输入层与隐藏层之间的权值矩阵;b1为偏移向量。本文采用线性整流(ReLU)函数作为激活函数,这是因为相比signmoid函数,ReLU函数能够在节省计算量的同时减少参数之间的相互依赖关系,缓解过拟合问题的发生。
基于式(9),可以计算出在第i层隐藏层的输出vi为
vi=fa(wivi-1+bi)
(10)
(3)输出层。输出层的目标是拟合评分数据Rij,采用独热编码函数fe(神经网络中采用One HotEncode函数)将连续值转化为离散值,公式为
y=fe(Rij)
(11)

(12)
式中:fs为softmax变换函数,神经网络中采用softmax函数;wo表示输出层的权值矩阵;xl表示最后一层隐藏层的输出,其中变量l表示隐藏层的层数;bo表示输出层的偏移量。
(13)

(14)

(15)

3.2 计算用户与物品特征矩阵
神经网络的训练主要在于权值矩阵和偏移向量的学习,即对3.1节中wi(第i层神经网络的连接权值)与bi(第i层神经网络的偏移向量)进行学习。在模型训练前,需要计算用户物特征矩阵U与物品特征矩阵T,利用梯度下降法来计算各特征,算法步骤如下。
①K=random() ∥随机初始化二次项系数K
②U=randomMatrix() ∥随机初始化矩阵U
③T=randomMatrix() ∥随机初始化矩阵T
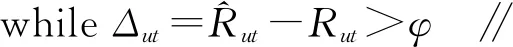


⑦ foru=1 tomdo


∥更新Uui
⑩ end for


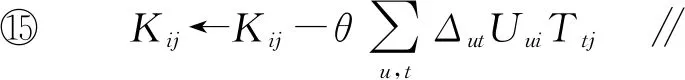
算法的输入参数为:用户项目评分矩阵R,用户数量m,物品数量n,用户特征维度a,物品特征维度b,收敛阈值φ,学习率θ。输出参数是用户特征矩阵U与物品特征矩阵T。第①~③行分别对二次项系数值K、用户特征矩阵U及物品特征矩阵T进行初始化;第④行判断是否达到收敛条件;第⑥行对常数项参数h进行更新;第⑦~⑩行循环m次,首先对eu进行更新,第⑨行更新Uui;第~行循环n次,第行对ft进行更新,第行更新Ttj;第行对二次项系数进行更新;第行输出用户特征矩阵U与物品特征矩阵T。
算法中需要设置一个较为合适的θ,θ太小会导致收敛的速度很慢,θ太大则会妨碍收敛,导致损失函数在最小值附近波动甚至偏离最小值。优化学习率θ最根本的思想为:在方向导数较大的地方设置较小的θ;在方向导数较小的地方设置较大的θ。在实践中,学习率θ的优化通常有二分线性搜索、回溯线性搜索和Armijo准则共3种,本文采用最简单的二分线性搜索,通过设置参数区间[θ1,θ2],不断地将区间切分成两半,参数选择方法如下。
设梯度下降优化函数h为
h(θ)=h(x+θd),θ>0
(16)
式中:x表示当前点输入值;d表示搜索斜率。

通过以上算法完成对特征矩阵的计算和神经网络的权值训练后,可以利用训练后的模型去预测用户对未评分项目的评分。对预测结果进行排序后,利用topN算法得出预测得分最高的前N个物品进行推荐。
4 实验及结果分析
4.1 实验环境及数据集配置
实验的操作系统版本是Ubuntu 16.04,CPU版本是Intel Corel i7 6700K,内存16 GB,SSD大小为250 GB,显卡是NVIDIA GeForce GTX 1080,CUDA版本是8.0 for Ubuntu 16.04,深度学习框架是Caffe(convolutional architecture for fast feature embedding),具体版本是Caffe for Ubuntu 16.04。实验的测试数据集采用2组数据,具体情况如表2所示。

表2 实验数据集说明
4.2 评价指标及参数配置
平分绝对误差EMA与均方根误差ERMS适用于推荐系统中的评分预测场景,本文采用EMA与ERMS来进行算法准确度的评价。EMA评价指标表达式为
(17)
式中:Ωtest表示测试数据集;|Ωtest|表示测试数据集的数据量。
ERMS评价指标表达式为
(18)
EMA与ERMS越小,表明算法预测结果与用户真实评分结果越相近,算法预测准确率越高。
在参数设置方面:MovieLens数据集设置参数a=18、b=20、θ=0.01;Epinions数据集设置参数a=22、b=20、θ=0.01;在神经网络的输入层,神经元的个数为用户维度与物品维度之和,输出层的神经元个数为5,分别对应1~5的评分概率。
4.3 特征分析方法对比
本节将本文提出的利用QPR的特征提取方法与RaF、SVD及PMF这3种方法进行对比。实验过程中,将MovieLens及Epinions数据集随机分成80%及20%两份,其中80%部分是训练集,20%部分是验证数据集。2组数据集下不同特征提取方法的EMA对比结果如表3所示。
从表3可以看出:在MovieLens数据集下,QPR效果最好,PMF与SVD效果次之,RaF效果最差,QPR的EMA比PMF、SVD及RaF分别降低了1.2%、2.81%及6.54%;在Epinions数据集下,同样是QPR效果最好,PMF与SVD效果次之,RaF效果最差,QPR的EMA比PMF、SVD及RaF分别降低了1.3%、5.46%及6.27%。
分析表3可知:RaF在2组数据集上的效果最不理想,这是因为RaF直接将用户对全部物品的打分直接作为用户的特征表示,当评分矩阵高度稀疏时,造成了较为严重的特征值失真现象;SVD由于需要使用平均值填充缺失值(缺失值的预处理),使得计算出的特征值与实际值存在一定的误差;PMF与QPR都取得了不错的效果,二者的共同点是都规避了缺失值的影响,但是QPR相比PMF效果更好,这是因为QPR能够通过二次项计算更好地将用户与物品之间的相关性体现出来。
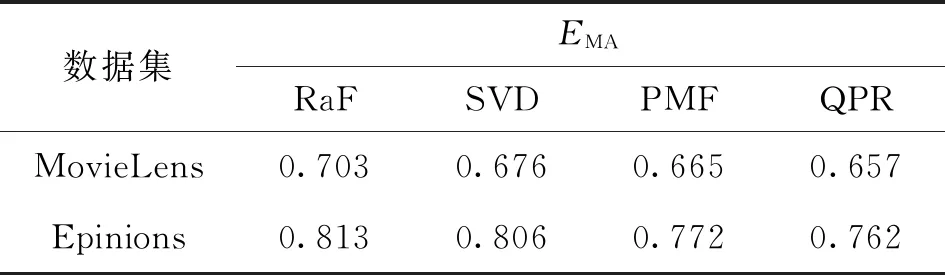
表3 2组数据集下不同特征提取方法的EMA
4.4 预测准确度对比
将本文QPR-NN算法与较新的主流推荐算法进行对比,评价指标使用EMA与ERMS,具体地,EMA与ERMS是在MovieLens与Epinions这2组数据集下分别执行算法5次后取的平均值。与本文算法进行对比的7个算法如表4所示,8种算法在2组数据集上的EA和ERMS如表5所示。

表4 QPR-NN对比算法的信息
对比8种算法在MovieLens数据集上的EMA可以发现:SVD[16]、PMF[27]、ItemBased[29]与Cluster[35]这4种算法比BPMF[32]、DsRec[34]、PMMMF[38]及QPR-NN的指标差;QPR-NN取得了最好的结果,相比SVD、PMF、ItemBased、BPMF、DsRec、Cluster、PMMMF,EMA指标分别降低了4.34%、3.36%、4.66%、1.54%、1.77%、3.62%及1.36%。对比8种算法在Epinions数据集上的EMA可以发现:QPR-NN相比其他7种算法在EMA指标值上取得了最优成绩;相比SVD、PMF、ItemBased、BPMF、DsRec、Cluster、PMMMF分别降低了7.09%、6.79%、5.4%、5.62%、1.98%、4.54%及3.29%。总体上对比EMA可以发现,QPR-NN在Epinions数据集上的性能提高比MovieLens多,可能原因是Epinions数据量相比MovieLens多,算法能够学习到的特征比较准确,从而预测的精度较高。

表5 8种算法在2组数据集上的EMA与ERMS
对比8种算法在MovieLens数据集上的ERMS可以发现:ERMS指标性能最好的是BPMF,次之是QPR-NN,SVD、ItemBased及Cluster效果较差;QPR-NN相比SVD、PMF、ItemBased、BPMF、DsRec、Cluster、PMMMF分别降低了1.53%、1.38%、2.65%、-0.32%、0.35%、0.57%及1.35%。对比8种算法在Epinions数据集上的ERMS可以发现:QPR-NN实验结果最好,Itembased效果最差;QPR-NN相比SVD、PMF、ItemBased、BPMF、DsRec、Cluster、PMMMF分别降低了7.61%、4.46%、13.21%、1.73%、0.79%、0.33%及1.07%。总体上对比ERMS可以发现,在MovieLens数据集下,相同指标体系下的BPMF算法指标比QPR-NN好,但在Epinions中,QPR-NN比BPMF好,说明随着数据量的增大,QPR-NN算法性能更为优异。特别地,在数据集与算法相同的条件下,ERMS都要大于EMA,反映出ERMS对算法的评价比EMA严格一些,这是因为ERMS对预测误差较大的情况加大了惩罚因子的值。
4.5 隐藏层参数优化
对于用户特征维度参数a、物品特征维度b、数据量参数m与n,已知的是模型准确率会随着特征维度与数据量参数值的增大而提高。但是,神经网络中隐藏层的数量l将对算法性能产生巨大影响:过小的l将影响算法达不到最优性能,过大的l将影响算法的计算效率。表6为参数l对EMA的影响。

表6 参数l对EMA的影响
从表6可以发现:当l=3时,算法的EMA指标达到最优状态;当l逐渐增大时,EMA也逐渐增大,计算效率也会随之下降。
5 结 论
大数据时代数据的爆炸式增长使得传统的推荐算法已不能适应数据高规模及高稀疏性的特点,已有工作从移植现有推荐算法到分布式平台,或与深度学习算法进行结合这2种思路去解决这个问题。在与深度学习算法进行结合的研究中,大部分工作是利用深度学习算法作为训练模型去处理推荐系统的数据,而在输入数据的特征提取方面,往往采用传统的处理方法(如RaF、SVD及PMF等),并没有更多考虑到两者之间的适配度问题。所以,本文利用深度学习数据建模方法通用性的特点,提出一种结合二次多项式回归与神经网络的推荐算法QPR-NN。首先,在对RaF、SVD及PMF等特征提取方法缺陷分析的基础上,为充分挖掘用户与物品之间的相关性,提出利用二次多项式回归模型对用户对物品的评分数据进行特征提取及降维;其次,将特征提取后的数据作为深度学习训练模型的输入,增加输入数据与训练模型之间的匹配度,并将训练得到的模型用于推荐评分预测;最后,通过与SVD、PMF、ItemBased、BPMF、DsRec、Cluster及PMMMF这7种主流推荐算法对比实验,证明了QPR-NN算法的有效性。下一步工作将主要集中在将本文推荐模型应用到更为广泛的推荐场景,从而提高模型的应用适应度。
