威布尔分布下小样本P-S-N曲线拟合方法

白恩军,黄树涛,谢里阳

(1.沈阳理工大学汽车与交通学院,110159,沈阳;2.东北大学航空动力装备振动及控制教育部重点实验室,110819,沈阳)

P-S-N(失效概率-应力-循环次数)曲线是工程上评估结构件和零部件疲劳可靠性的有力工具,学者提出了包括大样本和小样本疲劳寿命数据的多种P-S-N曲线拟合方法[1-5]。通过拟合大样本疲劳寿命数据可以直接获得统计参数。在一些小样本的统计分析中,经常借助贝叶斯方法获得疲劳寿命分布的统计参数,或者改进大样本数据的统计方法,使其适合小样本数据的统计分析[6-9]。

惠民等提出了疲劳寿命服从对数正态分布的小样本数据统计分析异方差回归的分析方法[10]。刘潇然等提出了基于非嵌入多项式混沌展开及贝叶斯更新方法的小样本中等寿命区P-S-N曲线预测方法[11]。赵永翔等提出了拓展极大似然法的3参数P-S-N曲线预测方法[12]。盛兴旺等提出了基于小样本数据的构件疲劳破坏全寿命区的双对数双折线S-N曲线拟合方法[13]。谢里阳等提出了基于样本聚集原理的疲劳寿命服从对数正态分布的小样本P-S-N曲线拟合方法[14]。一些学者应用神经网络和重构造等寿命疲劳曲线方法预测了复合材料的疲劳寿命及拟合材料的P-S-N曲线[15-17]。GB/T 24176—2009标准中详细地阐述了金属材料疲劳寿命服从对数正态分布的P-S-N曲线拟合方法[18],但是对于疲劳寿命服从威布尔分布的小样本P-S-N曲线,没有给出具体的统计分析和拟合方法。

因此,基于疲劳失效迹线的概念,疲劳寿命服从两参数威布尔分布的P-S-N曲线拟合方法相继提出[19-21]。本文基于疲劳失效迹线概念,根据半对数坐标下各级应力水平的疲劳寿命的均值(期望)和标准差与各级应力水平呈线性关系的假设,通过逐步改变线性关系系数,再根据每个线性方程将不同应力水平的疲劳寿命等效转换到最高应力水平,通过检验等效到最高应力水平的疲劳寿命的均值与已知的最高应力水平的均值的相对误差,确定假设的线性关系系数,反推疲劳寿命服从两参数威布尔分布的统计参数,实现了疲劳寿命服从两参数威布尔分布的小样本P-S-N曲线的拟合,并通过算例分析,证明了本文方法的可行性。

1 P-S-N曲线拟合原理

1.1 疲劳寿命等效转换

同一试件在不同应力水平下测试,得到的疲劳寿命数据在各级应力水平下具有相同的概率分位点[19-20]。基于此原理,本文提出服从两参数威布尔分布的小样本P-S-N曲线拟合方法。

对于威布尔分布,不同应力水平下具有的相同疲劳寿命概率分位点可表达为

P(ni,j)=P(nk,j)

(1)

式中:ni,j代表试件j在第i级应力水平的疲劳寿命;nk,j代表试件j在第k级应力水平的疲劳寿命;P代表失效概率。

因此,对于疲劳寿命服从两参数威布尔分布,将不同应力水平的疲劳寿命等效到最高应力水平,得到各参数的关系为

(2)

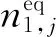
(3)

其中,Γ(x)代表伽马函数,Ei和Di分别代表第i级应力水平的疲劳寿命的均值(期望)和方差。

由于式(3)中包含3个伽马函数,在解λi和ηi时,无法写出显式表达式,因而采用逐步搜索法,具体步骤如下。

(1)将式(3)中的2个公式联合,写成关于形状参数ηi的等式,得到

(4)

令式(4)左侧为形状参数ηi的函数f(ηi),右侧为常数项Ci,得到

(5)

(2)令初值η0=0,步长Δη=0.001,ηk+1=ηk+Δη(k=0,1,2,…)。通过逐步搜索方法,计算f(ηi)与Ci的相对误差Δ,当Δ小于给定值(如0.001)时,则认为此ηi即为所求的解,公式为

(6)

1.2 疲劳寿命均值、标准差与应力水平的线性关系

根据式(3)解出疲劳寿命的均值(期望)Ei和方差Di,即可估算出各级应力水平疲劳寿命的统计参数,拟合P-S-N曲线。

大量试验研究结果显示,金属材料试样对数疲劳寿命的均值和标准差与应力水平呈线性关系[19-21]。图1为某铝合金试样疲劳寿命的均值和标准差线性拟合结果,置信度为95%。

图1 某铝合金板材试样疲劳寿命的均值和标准差

从图1可知,疲劳寿命的均值和标准差与应力水平呈线性关系。因此,半对数坐标下各级应力水平疲劳寿命的标准差σi与应力水平si的关系式为

σi=σ1+k(s1-si)

(7)

式中:σi代表第i级应力水平的疲劳寿命对数标准差;k代表对数标准差与应力水平关系直线的斜率。

从式(7)可知,只要找到一个合理的k,即可根据第1级应力水平疲劳寿命的标准差求解其他3级应力水平疲劳寿命的标准差。

2 P-S-N曲线拟合方法

通过式(7)将各级应力水平疲劳寿命等效到第1级应力水平,将等效后的疲劳寿命数据与第1级应力水平的疲劳寿命数据混合,计算混合后的疲劳寿命数据的均值与第1级应力水平的疲劳寿命均值的相对误差,确定合理的k和各级应力水平的疲劳寿命标准差,进而拟合P-S-N曲线,具体方法如下。

以4级应力水平为例。在做疲劳试验时,由于金属材料在高应力水平下疲劳寿命的分散性较小,并且疲劳试验过程时间较短,因此选择在最高应力水平上做15个试件,其他每级应力水平做3个试件,共需24个疲劳试件。

以疲劳试验方案15-3-3-3共24个疲劳试件为例,确定合理的k值和各级应力水平疲劳寿命标准差,并拟合疲劳寿命P-S-N曲线的方法如下。

(1)选择4级应力水平做疲劳试验,疲劳寿命的范围覆盖104～106次。在最高的应力水平s1做15个疲劳试件,并记录各试件的寿命为n1,j(j=1～15),其他3级应力水平各做3个疲劳试件,并记录各试件的疲劳寿命为ni,j(i=2～4,j=1～3)。

(8)

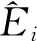
(3)由最小二乘法拟合4级应力水平对数疲劳寿命的均值(期望)的线性方程,并由此回归方程求解4级应力水平的疲劳寿命期望E1、E2、E3、E4。

(4)由式(7)估算其他3级应力水平的疲劳寿命的标准差,并令初值k0=0,ku+1=ku+Δk(Δk为增量,如10-5MPa-1)。由每一个假设的k确定的其他3级应力水平疲劳寿命的标准差,计算疲劳寿命的方差Di=102σi。由式(3)～(6)估算每级应力水平疲劳寿命的尺度参数λi和形状参数ηi。

(9)

若同时满足设定的相对误差条件(如Δ<0.001)和η1>η2>η3>η4,则说明k值和各级应力水平疲劳寿命分布参数值即为所求的合理的值。

由各级应力水平疲劳寿命的尺度参数λi和形状参数ηi可计算各级应力水平下不同失效概率的疲劳寿命分位点,进而拟合P-S-N曲线。

3 算例分析与讨论

3.1 拟合方法验证

传统方法使用各级应力水平所有疲劳寿命数据拟合疲劳寿命分布,进而获得各级应力水平的相同概率寿命分位点来拟合P-S-N曲线。为验证本文提出的疲劳寿命服从两参数威布尔分布的小样本P-S-N曲线拟合方法,以文献[21]中的齿轮疲劳寿命数据为例,与传统方法对比分析。齿轮疲劳寿命数据如表1所示。

表1 各应力水平下齿轮疲劳寿命数据[21]

为验证本文方法,利用表1中最高级应力水平的所有疲劳寿命数据,采用加权最小二乘法拟合出最高级应力水平的疲劳寿命分布参数,其他2级应力水平的计算则采用疲劳寿命数据的算术平均值,通过本文方法估算疲劳寿命分布参数。在Δ<0.001和k=0.025 MPa-1时,本文方法拟合的各级应力水平疲劳寿命统计参数如表2所示,拟合的可靠度为50%和90%的S-N曲线如图2所示。

表2 各级应力水平下的疲劳寿命的统计参数

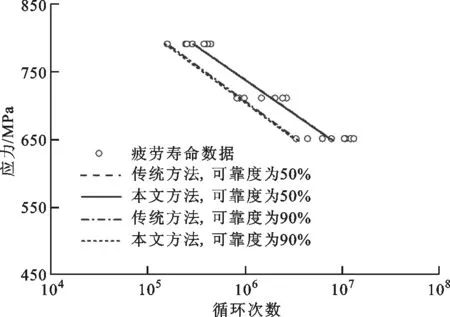
图2 本文方法与传统方法拟合的S-N曲线的对比

分析图2可知,本文方法拟合的可靠度为50%和90%的S-N曲线与传统方法的拟合结果在斜率上的相对误差分别为0.12%和0.41%,截距上的相对误差分别为0.01%和0.37%,相对误差均小于1%,说明本文方法拟合P-S-N曲线的效果较好。

3.2 不同拟合方案的对比分析

基于表1中的疲劳寿命数据,设计2个P-S-N曲线拟合方案如下。

方案1:假设使用最高级应力水平全部8个疲劳寿命数据,其他2级应力水平各使用3个疲劳寿命数据(表1中对应行前3个疲劳寿命数据),构成8-3-3疲劳寿命数据的P-S-N曲线拟合方案。在Δ<0.001和k=0.025 MPa-1时,应用本文提出的方法拟合此方案,得到各级应力水平下的疲劳寿命统计参数,结果如表3所示。

表3 采用方案1时各级应力水平下的疲劳寿命统计参数

方案2:使用最高级应力水平全部8个疲劳寿命数据,其他2级应力水平各使用5个疲劳寿命数据(表1中对应行前5个疲劳寿命数据),构成8-5-5疲劳寿命数据的拟合方案。在Δ<0.001和k=0.025 MPa-1时,应用本文提出的方法拟合此方案,统计参数如表4所示。

使用本文方法拟合以上2个方案的可靠度为90%的S-N曲线,并与传统方法拟合的可靠度为90%的S-N曲线进行对比,结果如图3所示。分析可知:本文方法拟合方案8-3-3与传统方法拟合的可靠度为90%的S-N曲线在斜率上相对误差为9.91%,截距上相对误差为5.4%;本文方法拟合方案8-5-5与传统方法拟合的可靠度为90%的S-N曲线在斜率上相对误差为9.31%,截距上相对误差为4.13%;本文方法拟合的S-N曲线在半对数坐标下,斜率和截距与传统方法的相对误差均在10%以内。

表4 采用方案2时各级应力水平下的疲劳寿命统计参数

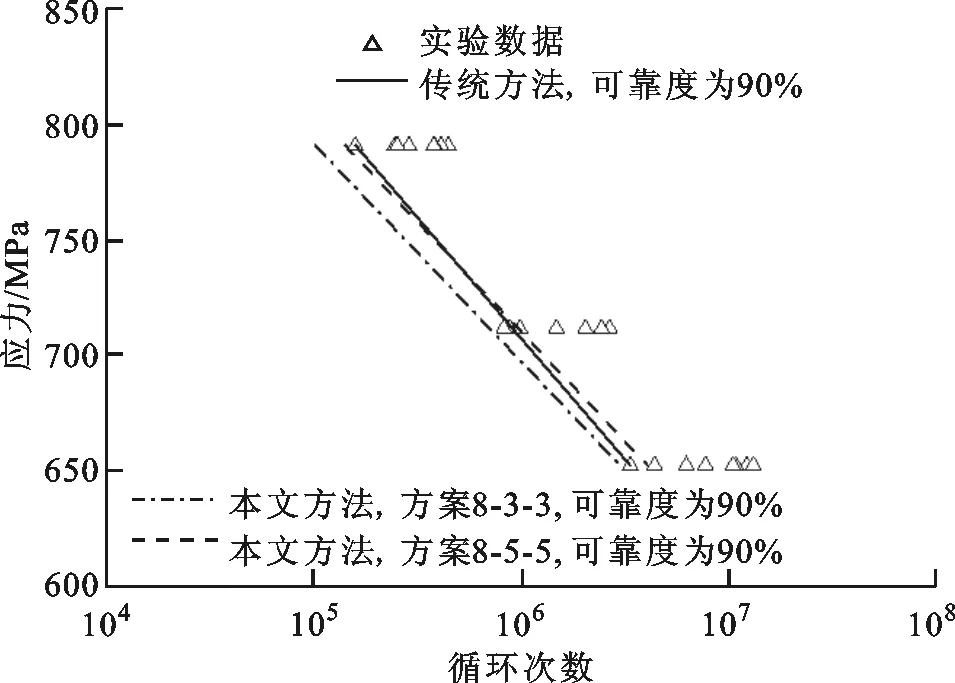
图3 2种方法拟合的可靠度为90%的S-N曲线

图4为本文方法拟合2种方案时,得到的疲劳寿命均值回归曲线,可以看出,本文2个拟合方案的疲劳寿命的均值与传统方法回归的疲劳寿命的均值存在一定的相对误差。由于2种拟合方案使用的疲劳寿命数据量不同,因而获得的疲劳寿命的均值存在差异。

图4 本文方法拟合2种方案的疲劳寿命均值回归曲线

由以上分析可见,当小样本试验疲劳寿命数据越接近母体寿命时,拟合P-S-N曲线的效果越好。本文方法相对传统拟合方法的优点是当试验数据很少,很难通过传统方法获得每级应力水平的疲劳寿命统计参数,或者获取较多试验数据的试验成本很高时,本文方法基于小样本数据就能够获得较为理想的拟合参数,拟合出疲劳寿命服从两参数威布尔分布的P-S-N曲线。

应用本文方法时,需要注意以下3点:①所有使用的数据需为有效数据;②如果试验数据分散性较大,在条件允许的情况下,在疲劳寿命数据分散性大的应力水平补做几个试件,是较有效的一种减小拟合相对误差的方式;③如果只有这些数据,无法再补充疲劳寿命数据,对于那些传统大样本方法无法解决的统计分析问题,本文方法也可以得到具有参考价值的结果,统计结果也是有一定意义的。

4 结 论

本文根据疲劳失效迹线概念,提出了疲劳寿命服从2参数威布尔分布的小样本P-S-N曲线拟合方法,基于文献[21]的疲劳寿命数据,应用本文提出的方法拟合P-S-N曲线,并与传统方法对比分析,结果显示:拟合方案8-3-3与8-5-5均可以拟合出较准确的P-S-N曲线;方案8-3-3和8-5-5与传统方法拟合的可靠度为90%的S-N曲线的斜率/截距的相对误差分别为9.91%/5.4%和9.31%/4.13%;本文方法可行。

本文将不同应力水平的疲劳寿命数据共享,极大地减小了试验成本,并能够拟合出较准确的结果。