三维叶盘失谐模态分析的摄动降阶方法

周子宣,徐自力

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安交通大学航天航空学院,710049,西安)

理想情况下,整体叶片轮盘具有循环对称性,并且每个扇区具有相同的几何形状和材料特性,因此可利用单个扇区的模型计算整体叶盘系统结构振动特性。然而,各个扇区的结构特性会由于制造公差、运行磨损等因素引入偏差,这种偏差称为失谐,失谐会导致振动能量集中和强迫振动响应幅值的急剧增加[1-2]。因此,在叶盘设计过程中,须考虑失谐的影响,以防止由于结构高周疲劳引起的失效。早期失谐叶盘的研究主要利用集中参数模型和连续参数模型[3-4],分析结构参数对局部化程度的影响规律,但模型过于简化,无法直接对应较为复杂的叶片轮盘结构。随着计算机硬件的发展,逐渐利用三维实体有限元模型对轮盘结构进行分析[5]。Kan等利用完整有限元模型分析了Rotor#67失谐叶盘在科氏力作用下的响应特征[6],但由于复杂叶盘整体有限元模型包含大量自由度,对其进行完整计算分析需耗费大量资源,计算效率较低。

因此,有学者开发了各种降阶模型[7-9],在准确预测失谐叶盘振动特性的同时显著减少计算量。Bhartiya等利用降阶模型,从统计学角度给出了失谐分布与失谐频率之间的对应关系,但其简化程度较高,不适合针对复杂模型进行精确分析[10]。Madden等深入讨论了CMM方法中各参数对求解精度的影响[11]。徐自力等利用多重模态降阶方法对大型复杂叶盘转子结构进行了模态求解,与实验结果基本一致,具有较高的精度[12]。

由于失谐量是随机产生的,需要计算多种不同失谐分布情况下的叶盘模态,从而最大限度预测叶盘最危险的振动情况。利用常规有限元降阶方法能在一定程度上提高计算效率,但在失谐分布情况发生变化后,需对叶盘整体重新进行降阶并求解特征值,计算多种失谐分布下叶盘模态的时间成本仍然巨大。

本文提出了一种摄动降阶方法,该方法将失谐叶盘分为谐调部分与失谐部分,利用单次降阶结果,结合不同的失谐改变量,通过摄动方法将模态求解转化为摄动量与谐调矩阵乘积形式,省去了常规降阶方法中重新降阶与求解环节,从而提高了计算效率。

1 降阶方法

谐调叶盘周向各叶片与对应的轮盘满足循环对称特征,为降低模型处理的复杂程度,将相邻两只叶片的中心分割面作为扇区边界,划分得到若干几何形状相同的扇区。将叶盘扇区作为基本子结构可避免对形式相同的扇区质量刚度矩阵重复降阶,从而提高计算效率。

对单个叶片扇区采用固定界面模态综合法[13]进行降阶,子结构的原始振动微分方程为

(1)

式中:M为子结构质量矩阵;K为子结构刚度矩阵;f为子结构界面力矩阵。

将运动方程中的刚度矩阵、质量矩阵和界面力按子结构内部和对接界面自由度分块,则运动微分方程可写为

(2)

式中:uI为需缩减的内部节点自由度;uF为子结构对接界面自由度;f为子结构的界面力。

采用固定界面模态综合法时,将子结构内部任意节点位移表示为界面固定时的节点位移与界面位移相对节点的牵连位移之和,即

(3)

式中:Ψn为界面节点固定时的主模态;Ψc为界面发生位移后的约束模态;n为主模态数目;nf为约束模态数目。由主模态与约束模态定义可得

(KII-ΛMII)Ψn=0

(4)

Ψc=-KII-1KIF

(5)

式中Λ为子结构特征值对角阵。

在结构振动分析中,由于只关注小部分低阶次的主模态,在此选取主模态Ψn的前k阶Ψk,则子结构内部节点位移的降阶关系可表示为

(6)

式中T称为降阶转换矩阵。将式(6)代入式(2)并左乘TT,可得

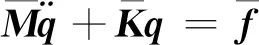
(7)

(8)

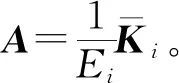
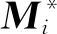
(9)

对刚度阵和质量阵,可利用式(6)中的转换矩阵进行重新降阶,得到广义坐标下带有失谐改变量的子结构振动微分方程

(10)

叶盘中将每个扇区作为一个子结构,系统的子结构与叶片数目N相同,对接形式如图1所示。根据位移协调条件,第i个子结构的左界面与第i+1个子结构的右界面位移一致;根据力平衡条件,第i个子结构的左界面力与第i+1个子结构的右界面力之和为0。由N个子结构组成的整体叶盘振动微分方程可表示为

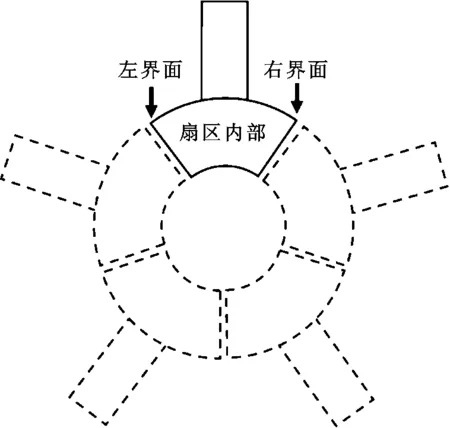
图1 叶盘扇区对接示意

(11)

式中

(12)

(13)

为方便级数展开,将多个子结构失谐量矩阵构成的整体失谐改变矩阵统一表示为一小参数ε*与矩阵乘积的形式

(14)

(15)

(16)

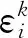
(17)

式中:Φp、Λp分别为失谐叶盘特征向量、特征值矩阵。将第i阶失谐模态振型与频率按ε*进行展开。由于叶盘失谐为小量,保留ε*的1次项进行近似计算,即

(18)

(19)

将式(18)(19)代入式(17),利用待定系数法,等式两端ε的1次项系数应相等,即

(20)

整理得

(21)

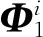
(22)

式中:Cj为对应项系数;ns为截取的谐调模态振型数量。

(23)

当i≠j时,利用正交振型规范条件可得

(24)

当i=j时,利用正交振型规范条件可得

(25)

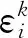
2 失谐叶盘模态计算

以NASA Rotor#67叶盘[14]为研究对象,采用摄动降阶法对失谐叶盘进行模态分析。叶盘整体结构如图2所示,叶盘整体结构共包含22个叶片扇区,每个扇区自由度为5.8万,整个叶盘自由度为128万。

图2 失谐叶盘整体结构

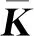
而在利用常规降阶方法(模态综合法)计算失谐叶盘模态时,计算按照图3右侧流程进行,在计算不同失谐分布情况下的叶盘模态时,需要重新定义失谐量并进行降阶。得到整体失谐矩阵后,再进行完整的特征值求解过程。摄动方法的优势在于利用了已有的谐调叶盘模态结果,只需考虑变化的失谐部分,将失谐频率与振型转化为式(21)、式(25)的矩阵乘积形式,计算速度高于完整矩阵特征值求解过程的速度,有效提高了失谐叶盘模态计算效率。

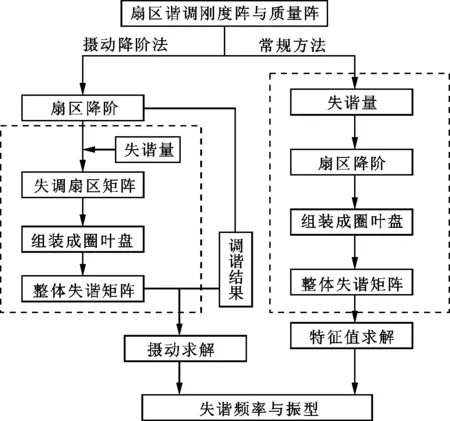
图3 摄动降阶方法与常规计算方法流程对比

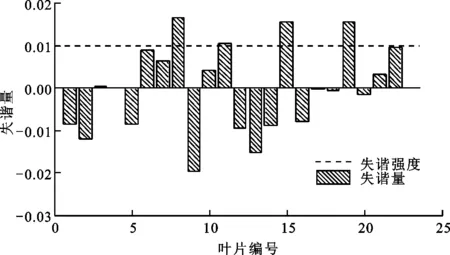
图4 随机失谐量分布情况

随机失谐量分布情况如图4所示,设定保留的模态阶次Ψk为100。利用摄动降阶法计算得到了该叶盘前100阶固有频率,对于同样模型,分别利用完整非降阶方法与模态综合法计算得到失谐叶盘的相同阶次固有频率,3种计算结果如图5所示,可知摄动降阶法的计算结果与完整法计算结果相吻合,叶盘频率分布呈现明显的阶梯特征,不同阶梯处分别对应不同的叶片振动阶次,在各个阶梯之间存在若干个叶片与轮盘相互耦合的过渡模态。

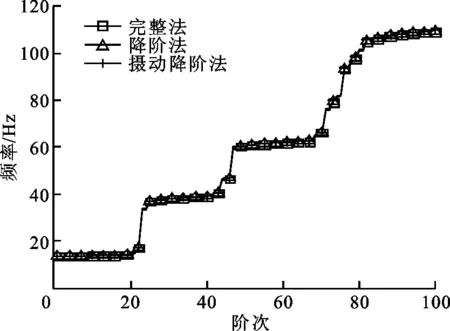
图5 叶盘前100阶模态频率分布

以完整法计算结果为基准,分别作出常规降阶方法与摄动降阶法计算前100阶模态频率的相对误差,固有频率计算相对误差随失谐强度σ的变化如图6所示。由图6可知:失谐强度为0.01时,摄动降阶法对固有频率的计算误差可以保持在0.25%以下;失谐强度增大至0.02后,摄动降阶法计算误差出现一定波动,大部分频率的计算误差仍维持在0.3%以下;失谐强度为0.03时,根据统计学原理,失谐量最大将达到6%,叶片间刚度的误差已达到极端值,实际工况下已很难发生,误差仍控制在0.3%左右,说明该算法在失谐强度为0.03以内时具有较好的精度稳定性。

失谐强度为0.01时分别统计了3种方法计算前100阶模态的耗时,如表1所示。当Ψk取为100时,完整法计算时间为320 s;常规降阶法计算时间为34.5 s,约为完整法计算时间的9.4%;摄动降阶法计算时间为11.2 s,约为完整法的3.5%。常规降阶法采用完整矩阵特征值来求解,而摄动降阶法采用失谐矩阵与谐调矩阵乘积的形式计算特征值,其计算效率高于常规降阶法。

当Ψk数目由100增至800时,利用常规降阶方法计算时,特征值求解的时间复杂度为O(n3)[15],降阶整体矩阵维度变为原来的8倍,计算时间将显著增加,总耗时由34.5 s增至185.2 s。摄动降阶法仅计算振型向量与矩阵的乘积,计算复杂度为O(n2),计算耗时相对于常规降阶法大大降低,总耗时仅由11.2 s增至24.2 s。摄动降阶法在较高的主模态数目下,计算失谐叶盘固有频率仍具有较高的效率。

(a)σ=0.01

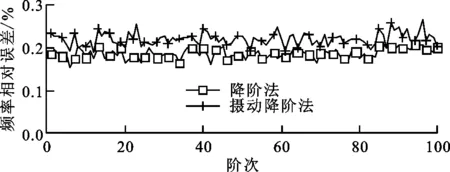
(b)σ=0.02

(c)σ=0.03图6 固有频率计算相对误差随失谐强度的变化

Ψk计算时间/s完整法常规降阶法摄动降阶法10032034.511.220032052.313.040032099.917.9800320185.224.2

进一步讨论保留主模态阶数对计算精度的影响,失谐强度为0.01时,将保留的主模态阶数分别增至200、400后,再次对比了摄动降阶法与常规降阶法的计算误差,如图7所示。当k=200时,摄动降阶法的计算误差波动程度较图6b降低至0.2%以下。提高Ψk数至400,摄动降阶方法计算误差进一步降至0.15%以下。较多主模态数可以保留更多的子结构振型信息,摄动降阶法利用该部分原始数据对失谐结构进行求解,故提高Ψk数可显著降低摄动降阶法的计算误差。考虑整体前100阶模态可满足分析需求,保留主模态Ψk数为整体模态数目的4倍时,即可保证较高的计算精度。

(a)Ψk=200

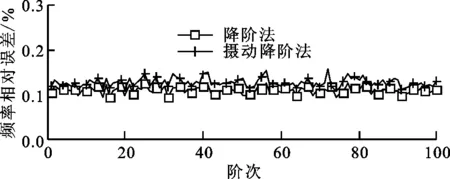
(b)Ψk=400图7 各阶模态频率计算相对误差随Ψk数的变化

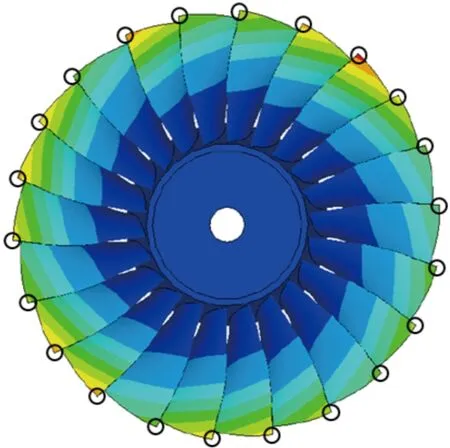
图8 完整法第2阶模态位移云图与叶尖节点位置示意

为突出失谐特征对振型的影响,取各叶片叶尖处节点位移进行讨论,节点位置如图8所示。将22只叶片按照顺时针顺序依次编号为1～22,分别提取完整法与摄动降阶法计算得到的叶盘第2阶与第3阶模态中叶尖相同位置的模态位移,不同阶次下摄动降阶方法模态位移计算结果图9所示,可知摄动降阶方法计算结果与完整法的结果吻合,叶盘发生失谐后,相邻叶尖模态位移出现突变,发生了模态局部化现象。

(a)阶次为2

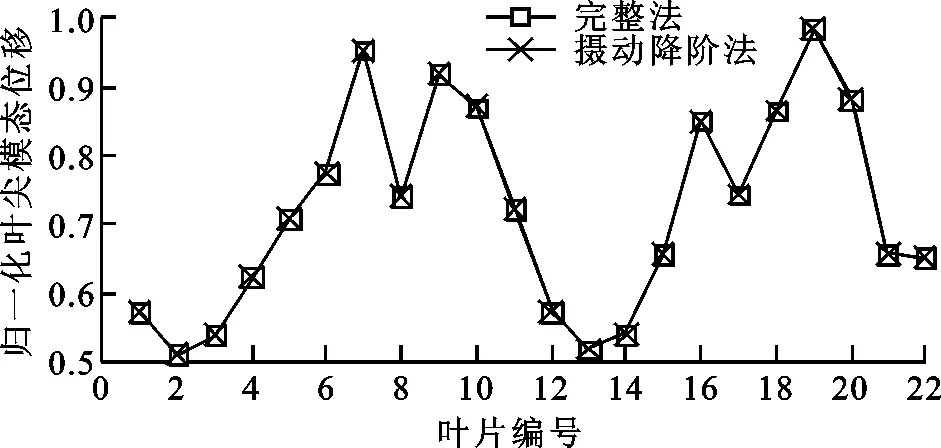
(b)阶次为3图9 不同阶次下摄动降阶方法模态位移计算结果

保持失谐强度为0.03,统计了第7、14、21只叶片叶尖前100阶归一化模态位移的计算误差,叶尖节点归一化模态位移计算误差如图10所示,可知计算误差基本小于0.25%,其中第20、40、70阶左右计算误差波动较为明显。对比图5可知,该模态阶次属于叶片轮盘耦合过渡模态,此时耦合作用使振动的非线性性质显著,而摄动方法以线性展开逼近精确解,此区域的计算误差有所波动,但总体依然保持在0.25%以下,满足工程计算精度要求。

(a)阶次为22

(b)σ=0.03图10 叶尖节点归一化模态位移计算误差

3 结 论

本文提出了一种用于计算失谐叶盘模态的摄动降阶方法,以Rotor#67叶盘作为算例进行验证。在随机失谐强度为0.01时,摄动降阶方法对前100阶频率计算误差在0.15%以下,失谐强度增加至0.03后,固有频率的计算误差低于0.3%,叶尖模态位移的计算误差低于0.25%,具有较高的精度稳定性。保留的主模态阶数为整体模态数目的4倍时,可保证较高的计算精度。在计算效率方面,主模态数为100时,摄动降阶方法计算时间仅为常规降阶法计算时间的30%。分析复杂结构叶盘在多种不同失谐分布形式下的振动特征时,摄动降阶法可加快叶盘固有频率与振型的计算速度。

本文方法主要针对单级叶盘进行分析,后续可在本方法基础上针对多级叶盘轴耦合结构开发出面向多部件系统的摄动降阶方法,考虑各部件之间的相互影响,从而更加精确地分析失谐叶盘转子系统的动力学特性。