系统模型建模方法探索及实践

陈大广 杨国诗 周全

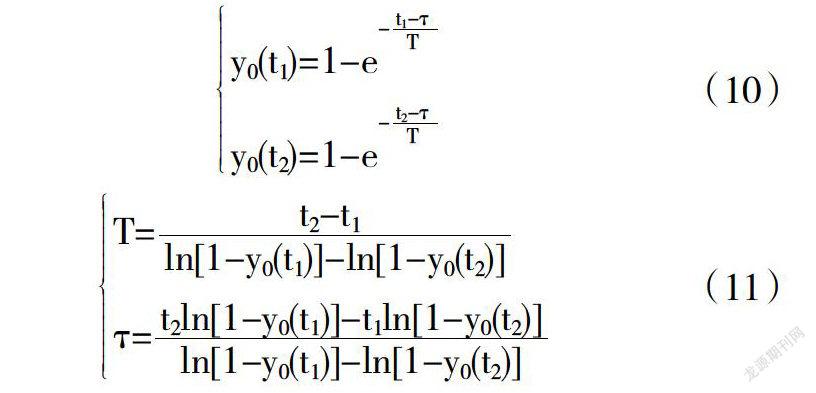
摘要：系统建模是设计控制系统首先要完成的工作，其工作对控制系统的控制算法的选取，控制设备的选用具有指导性作用.本文以某公司中型高炉为例，分别说明系统建模的方法、模型结构的确定、模型参数的求取及验证仿真过程等.充分展示了建立不同控制对象的模型建立及验证的方法过程，为工程技术人员设计控制系统，提供一定的方法支撑.

关键词：建模;高炉顶压;仿真

中图分类号：TP311.13  文献标识码：A  文章编号：1673-260X（2019）02-0043-03

建立被控过程对象的数学模型的目的在于：为设计过程控制系统、整定控制器参数提供依据;指导生产工艺及其设备的选型;被控过程及新型控制策略的仿真分析和研究;工业过程的故障检测与诊断系统设计.

1 系统建模方法

被控过程的数学模型描述过程的输入变量与输出变量之间的定量关系.这里，输入变量包括作用于过程的控制作用和干扰作用;输出变量为过程的被控变量.输入变量到输出变量的信号联系称为通道.其中，控制作用到输出变量的信号联系为控制通道;干扰作用到输出变量的信号联系为干扰通道.

模型的建立途径可分为解析法和实验辨识两大类，亦可将两者结合起来[1].

1.1 机理演绎法

机理演绎法又被称为解析法或是白箱法.它是根据被控对象或过程的内在机理，运用已知的静态和动态平衡关系，用数学推理方法来建立数学模型的方法.该方法的特点是在系统设计前完成数学模型推导，模型不但显示了系统输入、输出之间的数学关系.同时给出了，系统状态的输入和输出间的关系，有利于不同系统方案设计和分析.但是采用机理建模的首要条件是对被控过程的特性和机理有较深入的理解，能准确地加以数学描述.对内在机理复杂，难以完全明确内部变化状况的被控过程，数学模型建立则非常困难.

1.2 实验辨识法

该方法也称为试验辨识与参数估计法或黑箱法.它根据被控过程输入、输出实验测试的数据，通过系统辨识和参数估计建立对象的数学模型，确定出模型结构和参数.该方法完全由系统外部的输入-输出特性来构建数学模型.对内在机理复杂的被控过程，它比机理建模相对容易.但是受数据所对应工况的限制，模型往往难以对外推广应用.

1.3 混合法

该法也被称为灰箱法.通常采用两种方式：

①对被控过程中机理比较清楚的部分采用机理演绎法推导其数学模型，对于机理不清楚或不确定部分采用实验辨识法获得其数学模型.该方法适用于多级被控过程.

②先通过机理分析确定过程模型的结构形式，然后利用实验辨识法确定模型中的参数.显然，混合法是将机理知识与实验数据相结合，比实验辨识法具有更好的推广能力，比机理模型简单.

综合上述几种建模方法，建模的步骤及他们之间的相互关系如图1所示.

2 模型结构的确定

前面已经介绍，顶压采用负反馈控制，高炉可认为是一个大容积滞后加纯滞后的对象，炉顶压力在其整个控制范围内，顶压特性是非线性的，而顶压有一个设定的控制值，在设定值附近的小范围内，高炉顶压可看成近似线性.在控制过程中需进行线性化，通常把高炉炉顶压力控制系统看成是一个线性系统，模型可以定性的描述为：

其中，Y为控制对象压力，t为控制时间，T为系统时间常数，Ki为放大倍数，Q为炉顶煤气质量流量，？子为纯滞后时间.设定控制器输出为u，而u正比于Q2，即KiQ2=Ku，将Ku带入式（1）并作拉式变换得：

故可得出系统的传递函数为一阶惯性加纯滞后环节模型，其中K为静态增益，T为系统时间常数，？子为高炉顶压的纯滞后时间[2].

3 模型参数的确定及仿真

在确定了传递函数具体形式以后，下一步的工作就是如何确定传递函数中各个参数.时域实验建模法的原理是人为加入一个扰动，通过测定被控对象的响应曲线，根据此响应曲线来求得对象的传递函数.测定响应曲线典型输入信号为阶跃信号或方波信号，其对应的输出信号曲线称为阶跃响应曲线（飞升曲线）或脉冲响应曲线.通过操作调节阀，使被控过程的输入产生一个阶跃或方波变化，得到被控量随时间变化的阶跃响应曲线或脉冲响应曲线;

系统的传递函数为一阶惯性滞后环节，具有上式（3）的形式.据拉式变换可知，它的阶跃响应曲线是一条负指数规律上升的曲线，为

求取一阶惯性纯滞后传递函数中参数的方法有两种，飞升曲线法和两点法，两点法实际中很少使用.

3.1 飞升曲线法

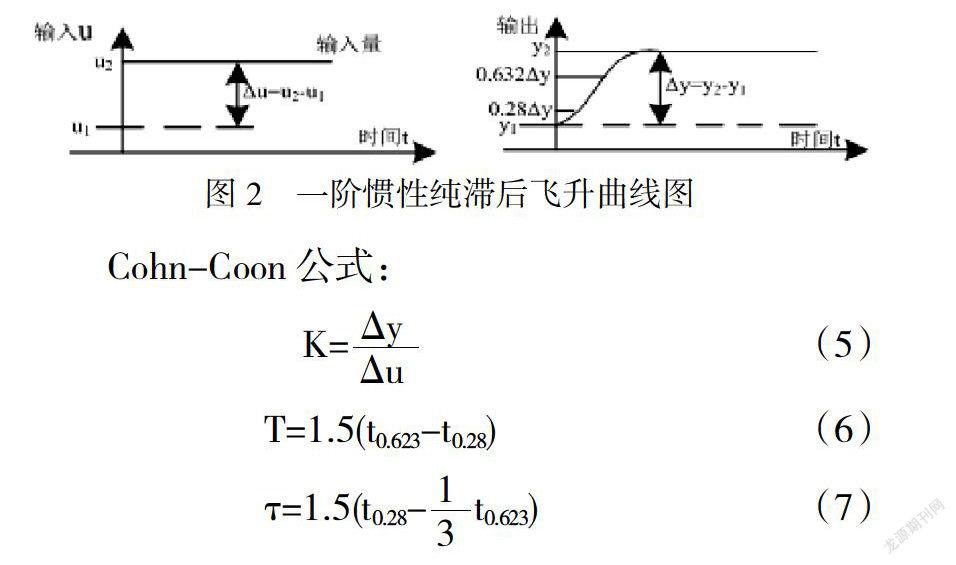
采用飞升曲线做实验，以获得对象的飞升曲线，然后用Cohn-Coon公式求对象参数.在允许范围内，改变调节阀开度，得到一阶惯性纯滞后对象的飞升曲线如图2所示.

式中K—对象放大增益;T—對象时间常数;？子—对象纯滞后时间;？驻u—系统阶跃输入;？驻y—系统相应的输出响应;t0.28—对象飞升曲线为0.28 时的时间;t0.623—对象飞升曲线为0.632？驻C时的时间.

3.2 两点法

要使求得的T和？子更加精确，可以在y0（t）曲线上多取几个点.以两点为一组求取T和？子，再将各组求得的T和？子值进行平均计算，获得最终的T和？子.从中看出，两点具有很大的任意性.因此，所得结果需要进行仿真验证，并且与实验曲线相比较[4].

在高炉正常生产过程中，在允许范围内改变调节阀开度，读入输入输出数据，并按以上飞升曲线法，经计算可得T=26.12s，？子=15.98s，K=0.55KPa/%.用两点法计算可得T=24.36s，？子=13.89s，K=0.51 KPa/%.最终取T=25s，？子=15s，K=0.53KPa/%.因此，可以得高炉炉顶压力的广义对象传递函数为：

模型验证是系统辨识不可缺少的步骤.通过调节阀门开度，重新得到一段阶跃响应曲线，用通过传递函数拟合出的曲线与实际曲线相比较.在时刻 调节阀刻度由15%加大到35%的一个阶跃，如图3所示：

炉顶压力的实际变化曲线和所建模型的响应曲线如图8所示，其中实线为实际变化曲线，点画线为模型响应曲线.

由图4的阶跃响应曲线的比较说明，模型仿真输出与高炉炉顶压力的实际输出吻合度较高，即通过辨识得到的炉顶压力传递函数能够反映实际对象的响应特性.该模型可以为高炉顶压控制系统分析和设计提供可靠的支持.

4 结束语

系统建模的精度是系统建模很重要的指标，是关系到控制系统性能指标的重要环节.在建模的过程中要依据对象的特性及可行性的要求进行，模型辨识出来后要进行验证性处理.从而得到精度符合控制系统要求的系统模型，为设计控制系统提供可靠依据.

参考文献：

〔1〕张嗣瀛，高立群.现代控制理论[M].北京：清华大学出版社，2015.

〔2〕段崇庆.炼铁高炉TRT系统炉顶压力控制的研究[J].信息技术与信息化，2015（4）：137-138.

〔3〕方康玲.过程控制系统[M].武汉：武汉理工大学出版社，2013.

〔4〕王正林，王胜开，陈国顺.MATLAB/Simulink与控制系统仿真[M].北京：电子工业出版社，2017.