强天然水驱油藏开发后期产液结构自动优化技术

雷占祥，穆龙新，赵辉，刘剑，陈和平，贾芬淑，周占宗

（1.中国石油勘探开发研究院，北京 100083；2.长江大学石油工程学院，武汉 430100）

0 引言

通常，油井产量的调整主要基于油井生产规律，利用数值模拟方法，制定一系列配产方案，再通过经济评价确定最终优化方案。但这种方法工作量大、周期长，且不能确保优化结果就是最优方案。近年来，国内外学者相继研究了基于最优化方法的油藏生产优化技术，如：非线性规划法[1-2]、伴随梯度法以及同时扰动随机逼近算法（SPSA）[3-4]等，取得了一定的应用效果。但这些方法大多倾向于仅从数学的角度求取经济效益最大值，而对油藏实际生产规律考虑较少，导致部分优化结果与油藏实际生产不相符[5-6]。为此，本文将油藏生产规律作为基础约束条件，建立最优控制数学模型，采用改进的SPSA算法对模型进行求解，并编制产液结构自动优化软件。将模型应用于强天然水驱油藏开发后期的产液结构优化调整中，以评估模型的实际应用效果。

1 产液结构优化模型

1.1 数学模型的建立

随着油田综合含水的不断上升，生产成本逐渐升高，经济效益日益降低，需要及时开展生产优化调整，即在最低的生产成本下得到最大的原油产量，实现油田控水稳油目标[7-9]。产液结构优化控制方法是通过优化油田单井产液量来实现开发效益最大化，一般采用净现值（NPV）来评估油田开发的经济效益。净现值法的优点是考虑了项目在整个计算期内的经济状况，以金额表示项目的收益情况，非常直观。

对于强天然水驱油藏来说，开发后期的生产成本主要受操作成本、污水处理成本等因素影响。因此，考虑操作成本和污水处理成本，建立经济净现值的优化目标函数：

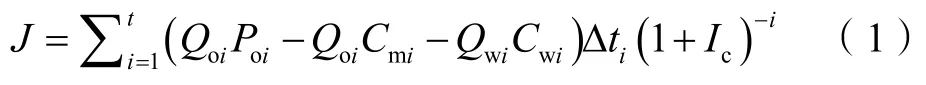
对于实际油藏，受储集层物性的限制，油井产液量的变化不能超过实际供给上限。同时，受地面集输能力和污水处理能力的限制，油藏产水量最大值不能超过集输能力和处理能力。因此，在进行优化设计时，需要增加模型的约束条件。边界约束是常见的约束形式，上边界需要考虑储集层供给能力和地面设施处理能力，下边界通常设为零，即关井。因此，产液结构优化数学模型的约束条件可表达为：

1.2 数学模型的改进

国内外学者基于上述数学模型，通过求解最优值，得到控制参数的优化结果。但由于上述数学模型没有考虑产量递减、水驱等油田生产规律，导致优化得到的产油量、含水率等变化规律与生产实际不符。为此，本文将油田生产规律作为基础约束条件，改进产液结构优化数学模型，建立以油田生产规律为约束的最优控制数学模型。

处于开发后期的强天然水驱油藏产油量变化和水驱特征都比较稳定，在开发方式不变的情况下，可以用目前的生产规律来预测后期的生产动态。本文采用Arps指数递减曲线和甲型水驱特征曲线来约束产油量和产水量的变化。其中，甲型水驱曲线表达式为：

将（3）式变形为：

对（4）式两边同时取自然对数，得到：

其中a=a0ln10b=b0ln10

按调整间隔进行分段后，利用（5）式求取i时刻的产水量为：

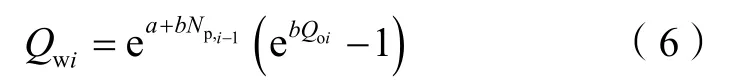
考虑到油田产液量变化，将当前产油量分为两个组成部分，即前一时刻自然递减对应的产油量和液量变化对应的产油量。由于开发后期的强天然水驱油藏产油量递减比较稳定，假定液量变化部分的递减规律与自然递减部分相同。产量递减公式可以写为：

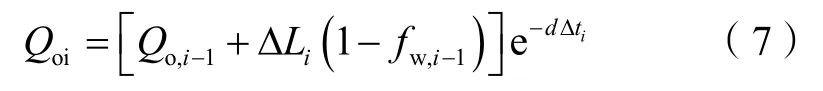
将（6）式和（7）式代入（1）式得到改进的目标函数：

由（8）式可知，产液结构的优化问题变为在约束条件下求取净现值的最大值，以及相应产液量最优的问题。对于该类最优化问题，常采用同时扰动随机逼近算法（SPSA）进行求解。

1.3 数学模型的求解

SPSA算法通过对控制变量进行同步扰动获得搜索方向，计算简便，每个迭代步只需对目标函数进行计算，不需要求解真实梯度，因此有效控制了计算复杂度。

假设控制变量维数为Nu，考虑进行N次扰动，则SPSA平均近似梯度[10-12]为：

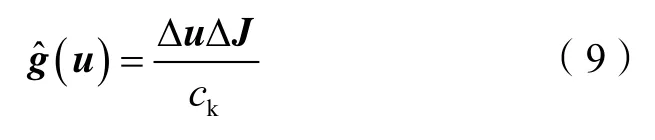
其中

借鉴标准SPSA梯度对（9）式进行改进得到：

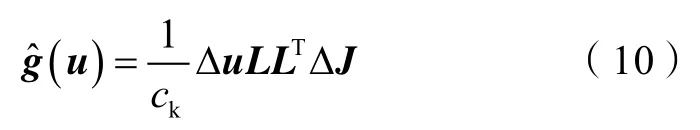
（10）式中，L为N维上三角方阵，当L为单位阵时，为标准SPSA算法。根据SPSA收敛性分析得到：

由（11）式可见，依然具有上山性。但是，L上三角方阵对近似梯度的精度有影响，需要进行调整，使近似梯度更接近真实梯度。由于梯度为向量，近似梯度与真实梯度越接近，则两者的夹角越小，对应的余弦值越大，余弦值计算公式为：

（12）式中的真实梯度是未知的。但是，每一个迭代步的真实梯度是确定的。因此，可以选择下式作为L的优化函数，使每个迭代步的计算梯度与真实梯度的夹角最小：

首先计算优化控制目标函数的近似梯度，然后根据约束条件，利用投影梯度法对近似梯度进行处理，进而更新迭代注采控制变量，得到最优控制变量：

2 产液结构自动优化软件

由于产液结构优化模型较为复杂，用数学方法求解析解非常困难，并且采用同时扰动随机逼近算法进行求解时，需要进行大量的随机扰动，计算量很大。所以，根据优化模型和求解算法的特征，设计了产液结构自动优化软件，大大提高了计算效率。

在软件设计时，严格遵循产液结构优化模型的求解过程，先根据油田的实际资料，确定模型所需的基础数据，如油田产油量、产水量、原油价格、污水处理成本等；然后，利用甲型水驱特征曲线和递减方程，拟合出模型的参数a、b、d等；再利用SPSA算法对产液结构优化模型进行求解，最终确定出产液结构的优化调整参数。

用SPSA算法求解产液结构优化模型的主要计算过程为（见图1）：①根据实际情况设定原油价格、产油量、递减率等模型基本参数；②初始设定每个时间点的液量变化为零，计算经济净现值J（Li）；③给定每个时间点的液量变化最大值（扰动步长），并用随机函数生成扰动方向，计算扰动生成的经济净现值J（Li±ΔLi）；④判断J（Li±ΔLi）与J（Li）的关系，若J（Li±ΔLi）大于J（Li），则将液量变化设定为Li=Li±ΔLi并重复②、③、④步，若J（Li±ΔLi）小于等于J（Li），则进一步判断循环次数是否超过设定次数；⑤若超过设定循环次数，则结束优化，若未超过设定循环次数，则重复③、④、⑤步。

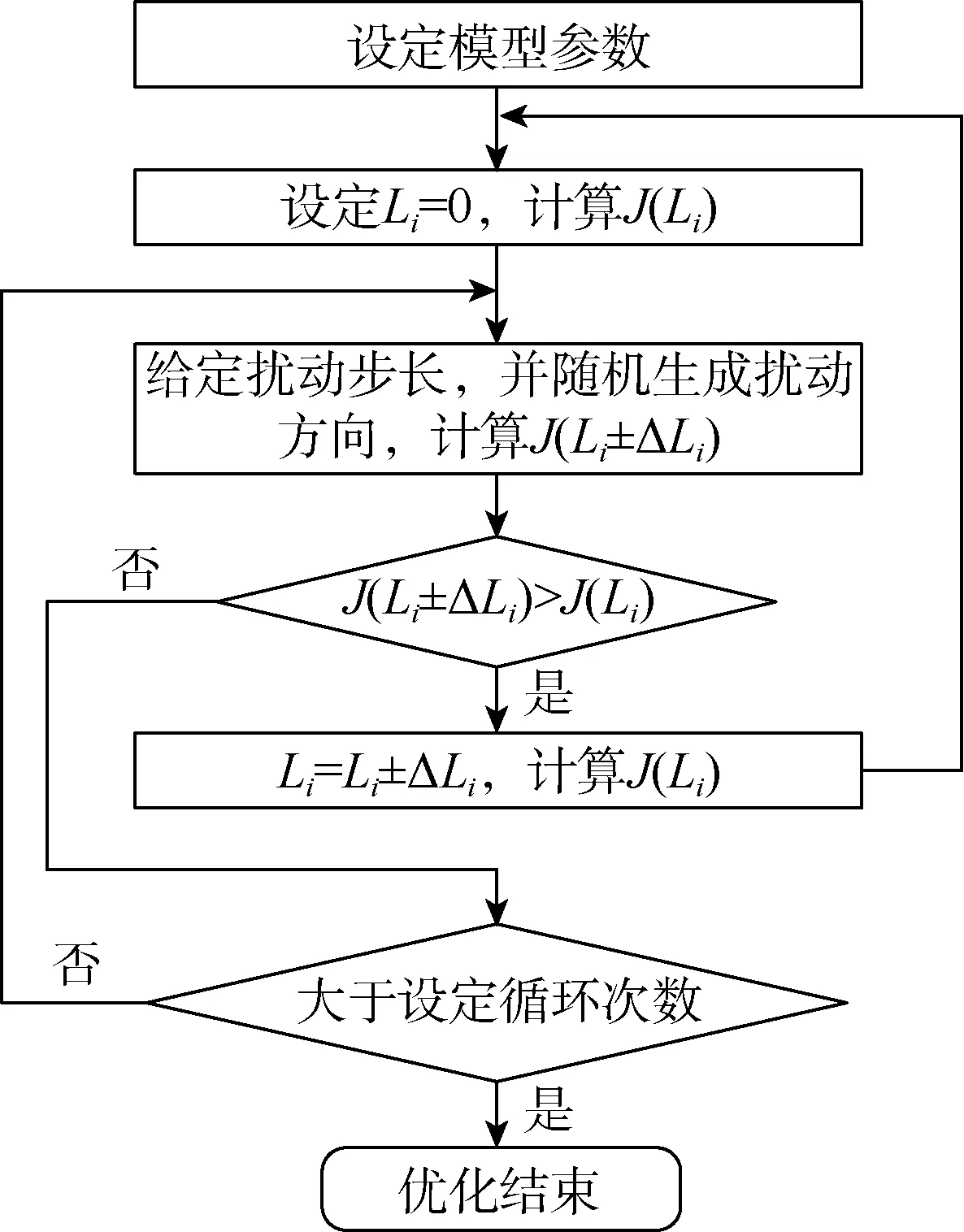
图1 产液结构自动优化流程图

3 应用实例

D油田位于南美洲厄瓜多尔热带雨林，其主力油藏M1为潮控河口湾沉积，孔隙度为20%～32%（平均值为25%），渗透率为（1 000～8 000）×10-3μm2（平均值为4 000×10-3μm2），具有很强的边底水，地饱压差为18.2～19.4 MPa，属于中高孔、中高渗、强边底水、低幅度、构造-岩性砂岩油藏。于1978年3月投产，边底水驱动为主，点状注水为辅，井网不规则，经过40年的开发，综合含水达到96.5%，目前处于开发后期。受储集层地质条件和资源国相关法规的限制，措施挖潜的难度大、作业成本高、经济效益有限。为实现油田开发后期效益最大化的目标，应用最优控制理论，建立并求解产液结构自动优化数学模型，实现了油田各单井的产液结构自动优化。

利用该区的产油量和产水量数据进行产量递减曲线和水驱特征曲线拟合。由于产量递减规律和水驱特征都较为稳定，拟合后相关系数都在0.99以上（见图2、图3）。

根据拟合结果，求得模型相关的基本参数a，b，d分别为-1.129 1，4.294 9，0.115 0。同时，根据油藏实际情况，设定原油价格为305.5美元/m3，原油操作成本为91.7美元/ m3，污水处理成本为1.8美元/m3。对D油田的管线集输能力和污水处理能力进行边界约束后，用改进的产液结构优化模型进行开发指标的优化和预测。

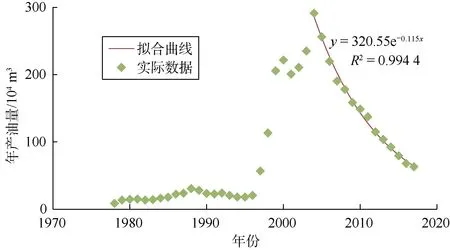
图2 D油藏产量递减曲线

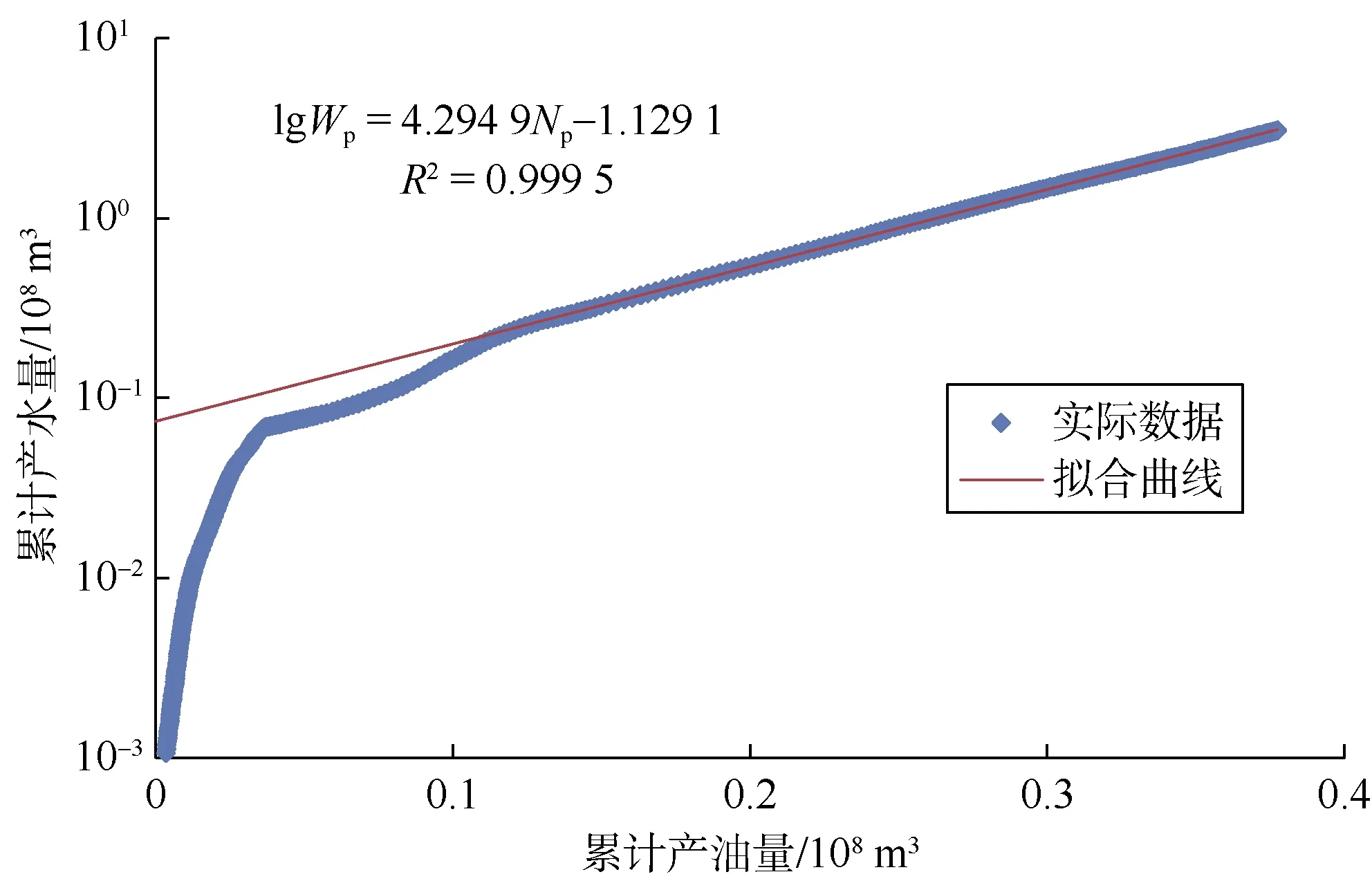
图3 D油藏水驱特征曲线

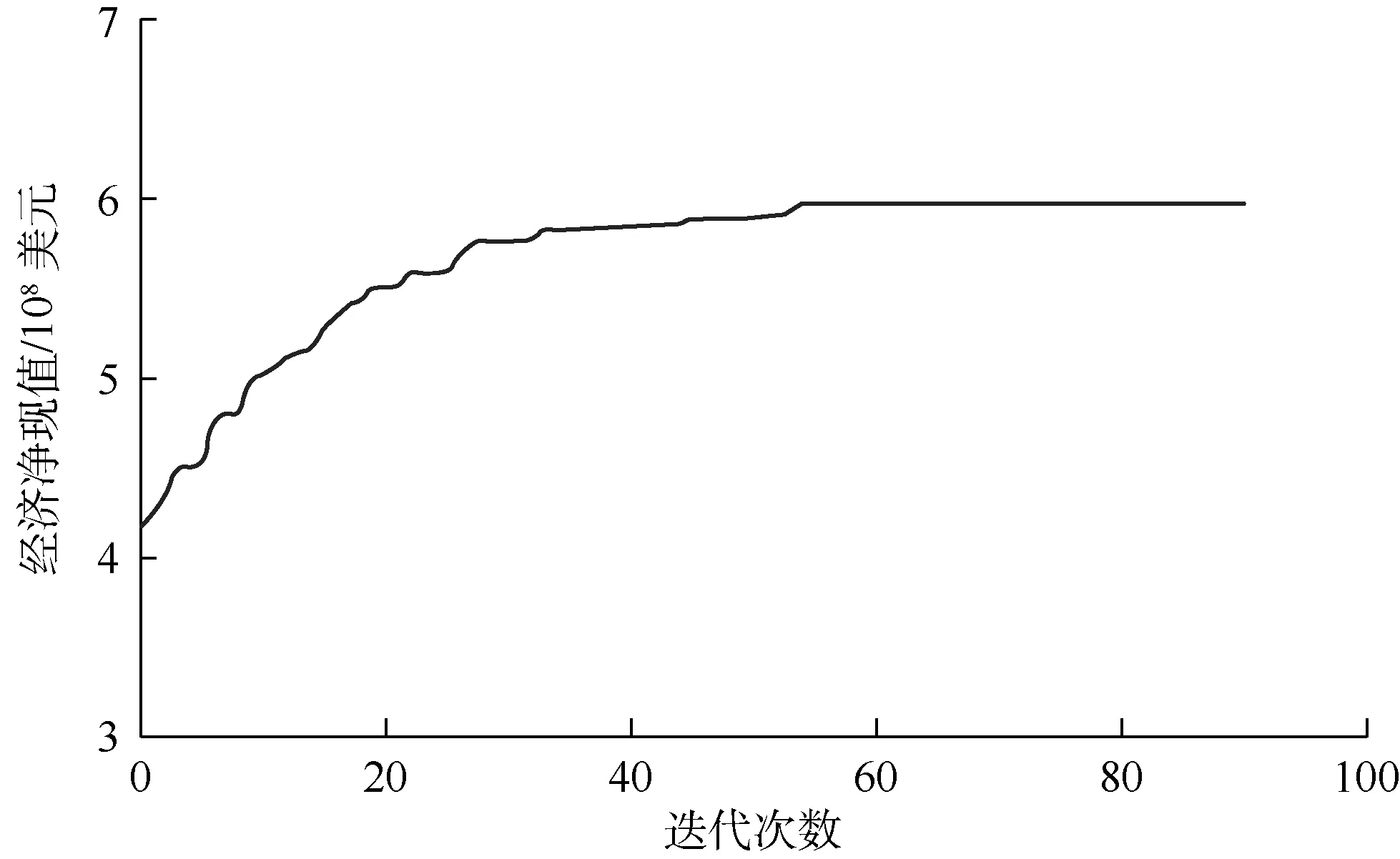
图4 自动优化过程中经济净现值变化曲线

图5 优化前后年产油量变化曲线

图6 优化前后年产液量变化曲线

图7 优化前后年含水率变化曲线

通过不断自动寻优，方案的经济净现值从4.15×108美元逐渐逼近至最佳经济净现值5.98×108美元，自动优化过程中经济净现值变化曲线见图4。根据优化结果（见图5—图7），提液期间年产油量增加，而保持液量生产期间年产油量递减明显，且递减率与D油藏实际递减率相同。预测期内的含水率平稳上升。对比优化前后的数据可知，优化后产液量明显提高，产油量也明显增加，含水率变化基本一致。产生这种结果的原因主要是两个方面：①油藏处于开发后期，可能以水驱冲刷的驱油模式为主，使含水率受液量变化影响较小；②油田污水以回注为主，成本较低，经济效益对产水量的增加不敏感。

4 优化方法对比

由于数值模拟方法广泛应用在国内外油田开发调整方案的制定过程中，具有权威性和普遍适用性。所以，将本文方法与数值模拟方法进行了对比分析（见表1）。

表1 数值模拟与产液结构自动优化对比

数值模拟方法的计算过程较为复杂，需要建立地质模型，准备数值模拟模型，进行历史拟合；根据产液量可能的变化范围，设计大量产液量调整方案，再进行预测对比。往往需要经过多轮优选，才能确定最终的优化调整参数。计算效率低、周期长、受数值模拟人员经验影响大，只能在设定的方案之间进行对比，还不能自动寻优。

本文方法的计算过程比较简洁，不需要建立复杂的地质模型，也无需进行反复的历史拟合；设定初值后，能够自动寻优，计算过程中不受人为因素影响。计算效率高、周期短。

5 结论

传统的优化控制模型仅考虑模型的数学极大值，而未充分考虑油田生产规律。针对此问题，将强天然水驱油藏开发后期的生产规律作为基础约束条件，建立了生产规律约束下的最优控制数学模型，避免了模型预测结果与生产规律不一致的问题。

利用SPSA算法对模型进行求解，编制产液结构自动优化软件，并应用在南美洲厄瓜多尔D油藏的开发生产实践中，实现了油田开发后期产液结构自动优化。

对比产液结构优化模型与数值模拟方法的优化过程，认为产液结构优化模型计算效率高、周期短、能够自动寻优，可满足油田开发后期产液结构的自动优化，也为同类油藏的开发调整提供参考。

符号注释：

a0，b0——甲型水驱特征曲线拟合常数；ck——扰动步长；Cmi——在i时刻的操作成本，美元/m3；Cwi——在i时刻的污水处理成本，美元/m3；d——产量递减率，f；fw,i-1——油田在i-1时刻的含水率，f；F（L）——近似梯度的优化函数；g——真实梯度；——近似梯度；Ic——基准收益率，f；J——经济净现值，美元；l——迭代序号；Li——油田在i时刻的产液量，m3/a；N——扰动次数；Np——累计产油量，m3；Np,i-1——油田在i-1时刻的累计产油量，m3；Nu——控制变量维数；Poi——在i时刻的原油价格，美元/m3；Qoi——油田在i时刻的产油量，m3/a；Qwi——油田在i时刻的产水量，m3/a；t——总时间，a；u——控制变量；ui——油田在i时刻控制变量；udi——控制变量的下约束边界；uui——控制变量的上约束边界；Wp——累计产水量，m3；θ——近似梯度与真实梯度夹角，（°）；ΔLi——油田在i时刻的产液量增量，m3/a；Δti——i时刻对应的时间间隔，a；Δupg——控制变量u的扰动间隔，p=1，2，…，Nu，q=1，2，…，N3；α——控制变量第l次迭代扰动系数。