考虑多因素的多层合采产液量劈分模式研究

周海燕，张运来，梁 潇，张吉磊，许亚南，刘继柱

（1.中海石油（中国）有限公司天津分公司，天津 300459；2.中国石油新疆塔里木油田公司勘探事业部，新疆 库尔勒 841000）

在油气藏剩余油气分布规律及后续开发方案研究中，储层的产量劈分是一个极为重要的技术环节，而多层合采中注水井的分层配注又是关键[1]，产量劈分又与分层配注密切相关，因此多层合采井产量劈分方法是研究各层动用状况和剩余油分布研究的基础[2-8]。建立一套切实可行，适用性强的产量劈分方法对油藏高效开发有着重要的现实意义。

目前，产量劈分方法主要有：①产液剖面系数法[9-11]；②地层系数（Kh）静态劈分方法[12-13]或流动系数Kh/μ劈分方法[14-16]（K为层段有效渗透率，h为层段有效厚度，μ为层段流体的黏度）；③有效厚度法[17]；④渗流阻力系数法[18]等。其中产液剖面系数法往往由于动态测试资料不全，使得劈分精度低、可信度差[19-20]。Kh值法对于储层非均质性较强、生产井段长、射孔层数多的薄互层砂岩油藏来说，其适用性较差[21-22]。有效厚度法没有考虑油藏的压差，物质平衡等因素。渗流阻力系数法无法确定影响因素对劈分方法的作用大小，使其适用性差。

以渗流理论为基础，利用数值模拟技术拟合岩心实验[23-25]，在此基础上，考虑不同的渗透率级差，通过数值模拟研究各层产液劈分模式，从而得到产液劈分方法及规律。

1 劈分系数公式理论基础

根据达西公式，可以得到产液量计算公式：

式中：q1为液流量，cm3/s；qw为水流量，cm3/s；qo为油流量，cm3/s；k为绝对渗透率，μm2；ΔP为压差，1.01×105Pa；L为渗径长度，cm；krw为水相相对渗透率；kro为油相相对渗透率；μw为水相黏度，mPa·s；μo为油相黏度，mPa·s。

而油水在地下渗流服从分流方程[26]：

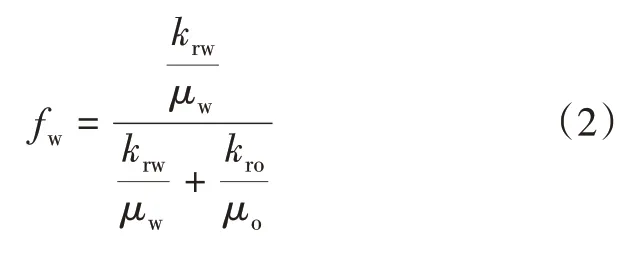
式中：fw为含水率。

结合式（1）—式（2）可以看出，产液量与岩石绝对渗透率k、生产压差以及含水率直接相关。该文研究多层合采条件下各层的产液劈分系数，产液劈分系数定义为各小层产液量与总产液量比值，相应计算见式（3）。在实际生产中，难以通过测试直接获取各小层产液量，需将各层产液劈分系数与其他易测参数建立关系，进而计算求取各小层产液状况。在建立参数关系的过程中，则需多因素综合考虑，应考虑产液劈分系数、生产压差、含水率、渗透率贡献率等参数之间的关系。影响因素的综合考虑使得劈分系数更加精确，适用性更强。

式中：Fi为小层产液劈分系数；qi为小层的产液量，104m3；Q为总产量，104m3。

研究时考虑了8组不同渗透率级差（低∶中∶高）：1∶3∶5、1∶3∶10、1∶3∶15、1∶3∶20、1∶3∶25、1∶3∶30、1∶3∶35、1∶3∶40。如果只考虑高低渗透层的级差，那么中渗透的影响将得不到体现，使结果出现偏差。为此，这里将对应的渗透率级差考虑成渗透率贡献率，储层内部分为高、中、低3种渗透性小层，则渗透率贡献率定义为某层渗透率数值与高、中、低各渗透层渗透率数值之和的比值，例如高、中、低渗透层渗透率级差为5∶3∶1，则高渗透层的渗透率贡献率为：5（/5+3+1）=0.56。

2 数值模型设置

基于矿场实际及实验测试结果建立数值模型（图1），建立上下共3层的数值模拟模型，模拟储层高、中、低渗透性级差条件下含水率、渗透率贡献率等参数对产液劈分系数的影响。模型网格数10×1×3，X方向步长为0.6 m，Y方向步长为3.2 m，Z方向步长为3.2 m，储层顶深2 000 m。由于多层合采难以直接测量获取各小层产液量，则建立模型采取分层独立生产，易获取单层产液劈分系数、含水率、渗透率等参数之间的关系。模型两端分别设置3口注水井（3口注水井名为I1、I2、I3，位于同一坐标位置）和3口生产井（3口生产井名为P1、P2、P3，位于同一坐标位置），各生产井分层射孔生产，各注水井分层射孔注水，注水井注水速度为50 m3/d，生产井产液速度为50 m3/d。模拟生产1个月，统计不同渗透层中（高渗透层、中渗透层、低渗透层）产液量、含水率、渗透率等数值。

图1 数值模型3D显示图Fig.1 3D figure of the numerical model

3 高渗透层产液量劈分模式研究

图2是8组不同渗透率贡献率时高渗透层产液劈分系数与含水率关系。可以看出，各组产液劈分系数与含水率关系呈现出非常一致的变化趋势：在含水率较低时，随着含水率上升，产液劈分系数稍有降低，而当含水率达到一定程度之后，随着含水率继续上升，产液劈分系数增大。定义此处无因次产液劈分系数为各组含水率为0时的产液劈分系数与代表组对应产液劈分系数的比值。因此，这里也选择1∶3∶5这组级差（此时高渗透层贡献率为0.56）作为代表组来得到产液劈分系数与含水率的变化关系（图3），再将各组含水率为0时的产液劈分系数比上高渗层贡献率0.56这组对应的产液劈分系数，得到当前各组无因次产液劈分系数（表1），从而得到无因次产液劈分系数与渗透率贡献率的关系（图4），最后就可以得到产液劈分系数与含水率和渗透率贡献率的关系。

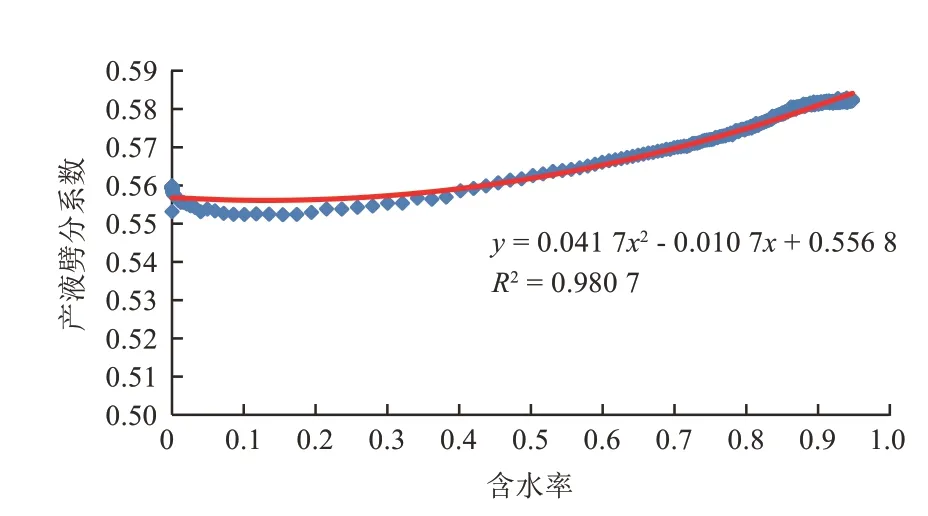
图3 产液劈分系数与含水率关系回归线（渗透率贡献率为0.56）Fig.3 Regression line of relationship between splitting coefficient and water cut when permeability contribution rate is 0.56

图4 无因次产液劈分系数与渗透率贡献率关系曲线（含水率为0）Fig.4 Relation curve between dimensionless splitting coefficient and permeability contribution rate when water content is 0

表1 无因次产液劈分系数与渗透率贡献率数据（含水率为0）Table 1 Data table of dimensionless splitting coefficient and permeability contribution rate when water cut is 0

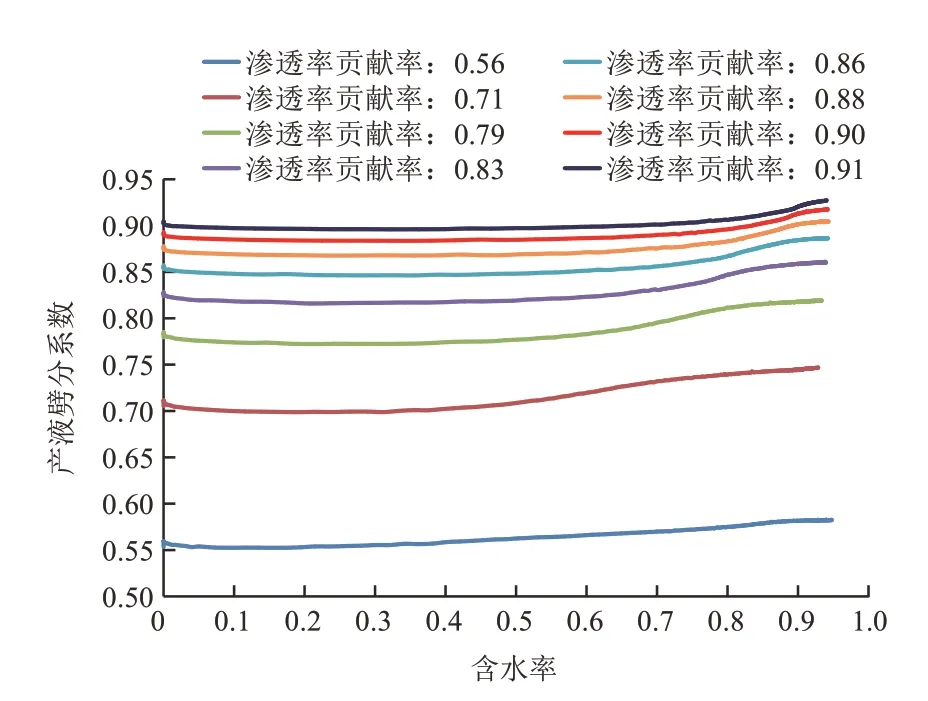
图2 高渗透层产液劈分系数与含水率关系（不同渗透率贡献率）Fig.2 Relationship between separation coefficient and water content of high permeability layer produced by different permeability contribution rates

产液劈分系数随含水率和渗透率贡献率的变化：

式中：Fl为产液劈分系数；Rk为渗透率贡献率。

4 中渗透层产液量劈分模式研究

图5是8组不同渗透率贡献率时中渗透层产液劈分系数与含水率关系。可以看出，曲线在含水率60%处发生变化，因此，这里也选择1∶3∶10这组级差（此时中渗透层贡献率为0.21）作为代表组得到产液劈分系数与含水率的变化关系（图6、图7），再将各组含水率为60%时的产液劈分系数比上中渗层贡献率0.21这组对应的产液劈分系数，同理得到当前各组无因次产液劈分系数（表2），最后得到无因次产液劈分系数与渗透率贡献率的关系（图8），这样就可以得到产液劈分系数与含水率和渗透率贡献率的关系。

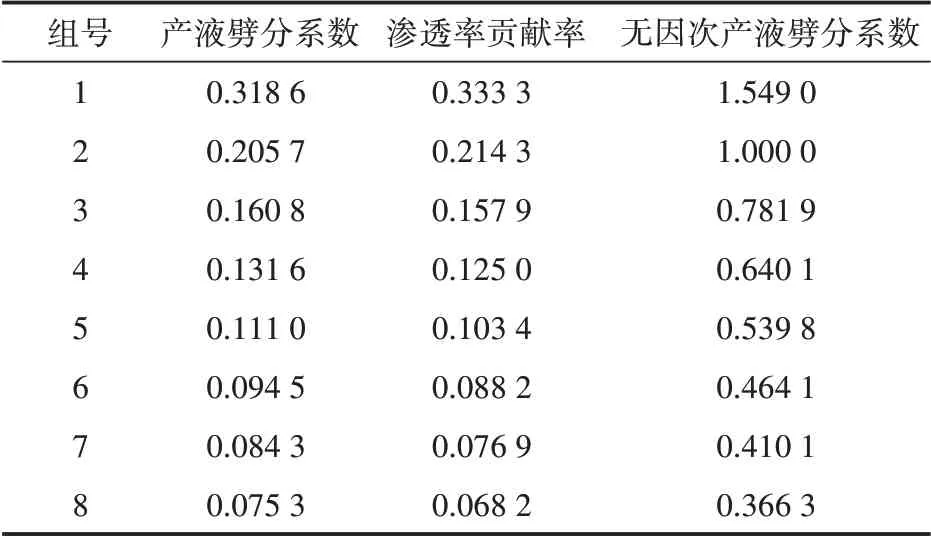
表2 无因次产液劈分系数与渗透率贡献率数据（含水率为0.6）Table 2 Data table of dimensionless splitting coefficient and permeability contribution rate when water cut is 0.6

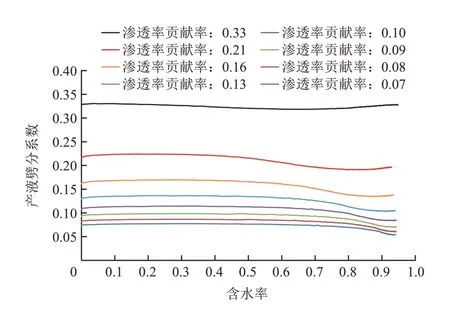
图5 中渗透层产液劈分系数与含水率关系（不同渗透率贡献率）Fig.5 Relationship between separation coefficient and water content of medium permeability layer produced by different permeability contribution rates

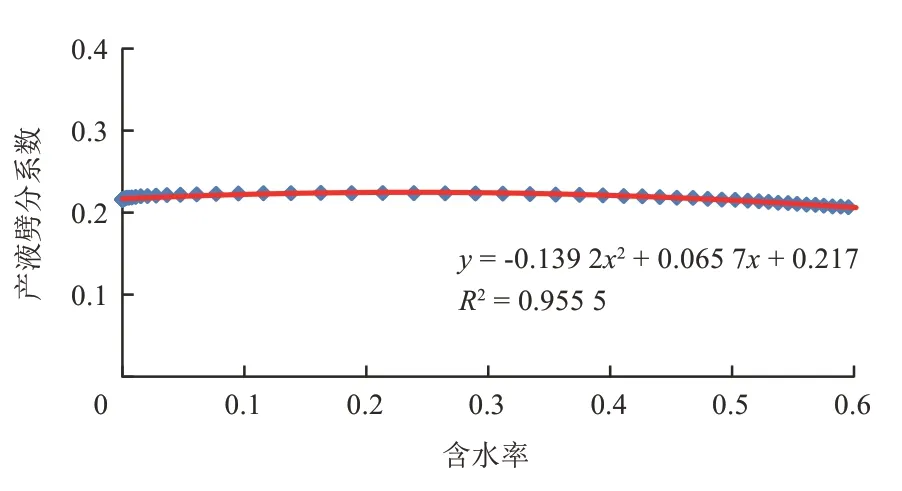
图6 产液劈分系数与含水率关系回归线（含水率小于60%，渗透率贡献率为0.21）Fig.6 Regression line of relationship between splitting coefficient and water cut when permeability contribution rate is 0.21（water cut is less than 60%）

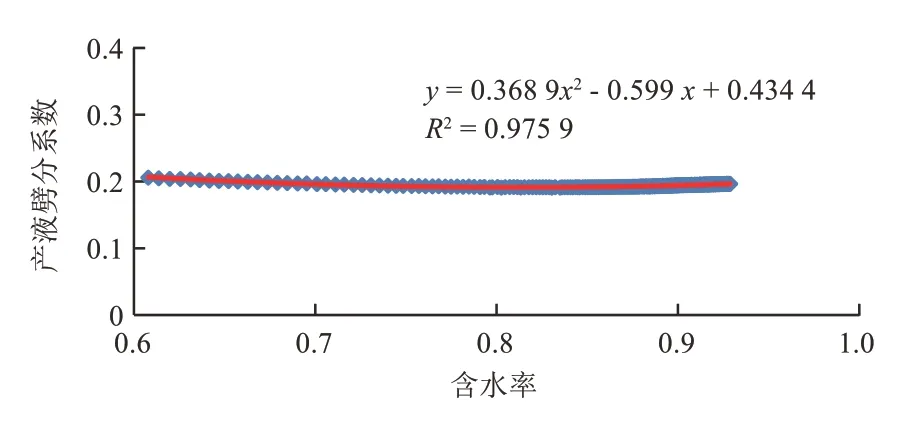
图7 产液劈分系数与含水率关系回归线（含水率大于60%，渗透率贡献率为0.21）Fig.7 Regression line of relationship between splitting coefficient and water cut when permeability contribution rate is 0.21（water cut is greater than 60%）

图8 无因次产液劈分系数与渗透率贡献率关系曲线（含水率为60%）Fig.8 Relation curve between dimensionless splitting coefficient and permeability contribution rate when water content is 60%

产液劈分系数随含水率和渗透率贡献率变化的关系式：

fw＜0.6时

fw＞0.6时

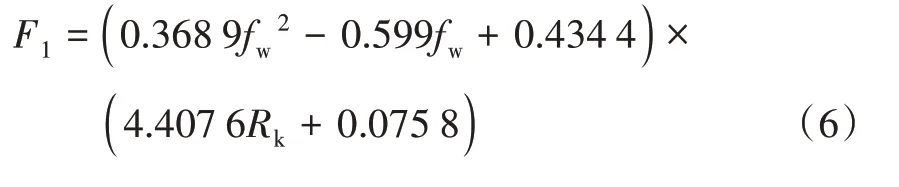
5 劈分模式检验

5.1 高渗层产液劈分模式检验

为了验证高渗层产液劈分模式的可靠性，根据9组并联岩心实验的含水率、渗透率贡献率，利用式（4）可以得到各组实验理论计算的产液劈分系数，与拟合得到的结果相比较即可很明显看到，结果基本上还是比较可靠的，各组产液劈分系数计算值与实际值见表3。可以看出，3、7、8三组实验符合相对较差外，其余6组均比较好。

表3 9组并联实验产液劈分验证结果（高渗层）Table 3 Verification results of nine sets of parallel experimental production liquids（high permeability layer）

5.2 中渗层产液劈分模式检验

为了验证中渗层产液劈分模式的可靠性，根据9组并联岩心实验的含水率、渗透率贡献率，利用式（5）、式（6）可以得到各组实验理论计算的产液劈分系数，与拟合得到的结果相比较即可很明显看到，结果基本上还是比较可靠的，各组产液劈分系数计算值与实际测试值见表4。可以看出，3、7、8三组实验符合较差外，其余6组均具有较高的符合程度，可以满足现场需要。

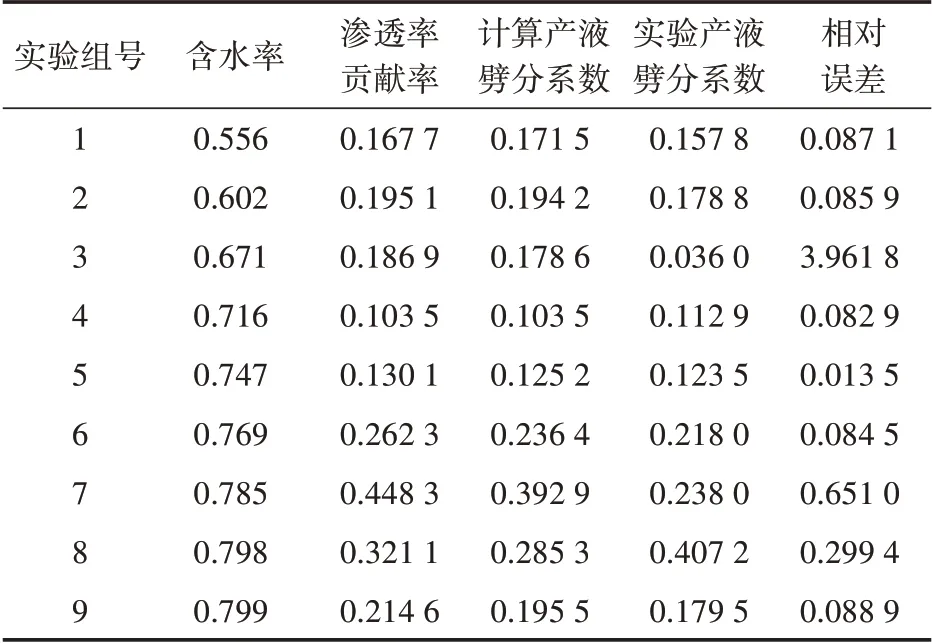
表4 9组并联实验产液劈分验证结果（中渗层）Table 4 Nine sets of parallel experimental production liquids verification results table（medium permeability layer）

至于低渗透层只需用1减去中高渗透层劈分系数即可得到。

6 结论

1）利用数值模拟方法，考虑高、中、低不同渗透层渗透率级差，研究渗透率贡献率、含水率、产液劈分系数等多项参数关系，提出了不同渗透层的多层合采产量劈分模式。利用多项式回归计算，建立了不同渗透层综合考虑含水率、渗透率贡献率的产液劈分数学模型。

2）通过数值模拟计算与实验测试结果对比检验，该劈分模式计算结果相对误差普遍较小、准确性较高，表明该劈分方法理论计算与矿场生产实际比较符合，能够满足现场应用的需要。