基于井下分离的深水双梯度钻井参数优化

王江帅，李军，柳贡慧, ，黄涛，杨宏伟

（1.中国石油大学（北京）石油工程学院，北京102249；2.北京工业大学，北京100192；3.中海油田服务股份有限公司，天津 300459）

0 引言

深水钻井面临着众多挑战，例如地层窄安全密度窗口、海洋地质灾害（浅层气、浅层水流、天然气水合物等）、深水低温、不稳定海床等[1-4]。其中，地层窄安全密度窗口直接影响深水钻井作业的安全高效性和成功率[5]。近几十年来，国内外分别研制了注气双梯度钻井[6]、注空心球双梯度钻井[7]、海底举升泵双梯度钻井[8]以及控制钻井液帽钻井[9-11]等，这些技术缓解了深水钻井窄密度窗口安全钻井问题[12-13]。

基于向环空内注入轻质物体（空心球、气体等）形成双梯度钻井的思想，本文设计了一种通过在钻杆上安装短节（分离器）来实现井筒内双密度的新型双梯度钻井方式，并进行了室内可行性实验。针对该钻井方式，提出了钻进过程中动态井筒压力计算方法，并基于此建立了钻井参数优化模型。模型以实现最大钻进深度为目标，尽可能地减小井底压差，并保证井筒压力始终在窄安全压力窗口内，有效避免了因压力不平衡导致的井下复杂情况，有利于安全高效钻井。

1 室内可行性实验

新型双梯度钻井实验装置如图1所示，通过在钻杆上安装分离器来实现井筒内双密度。经分离器分离后使得分离器上部环空空心球含量高，为低密度的混合流体；下部环空空心球含量低，为高密度混合流体，从而实现环空内双压力梯度。

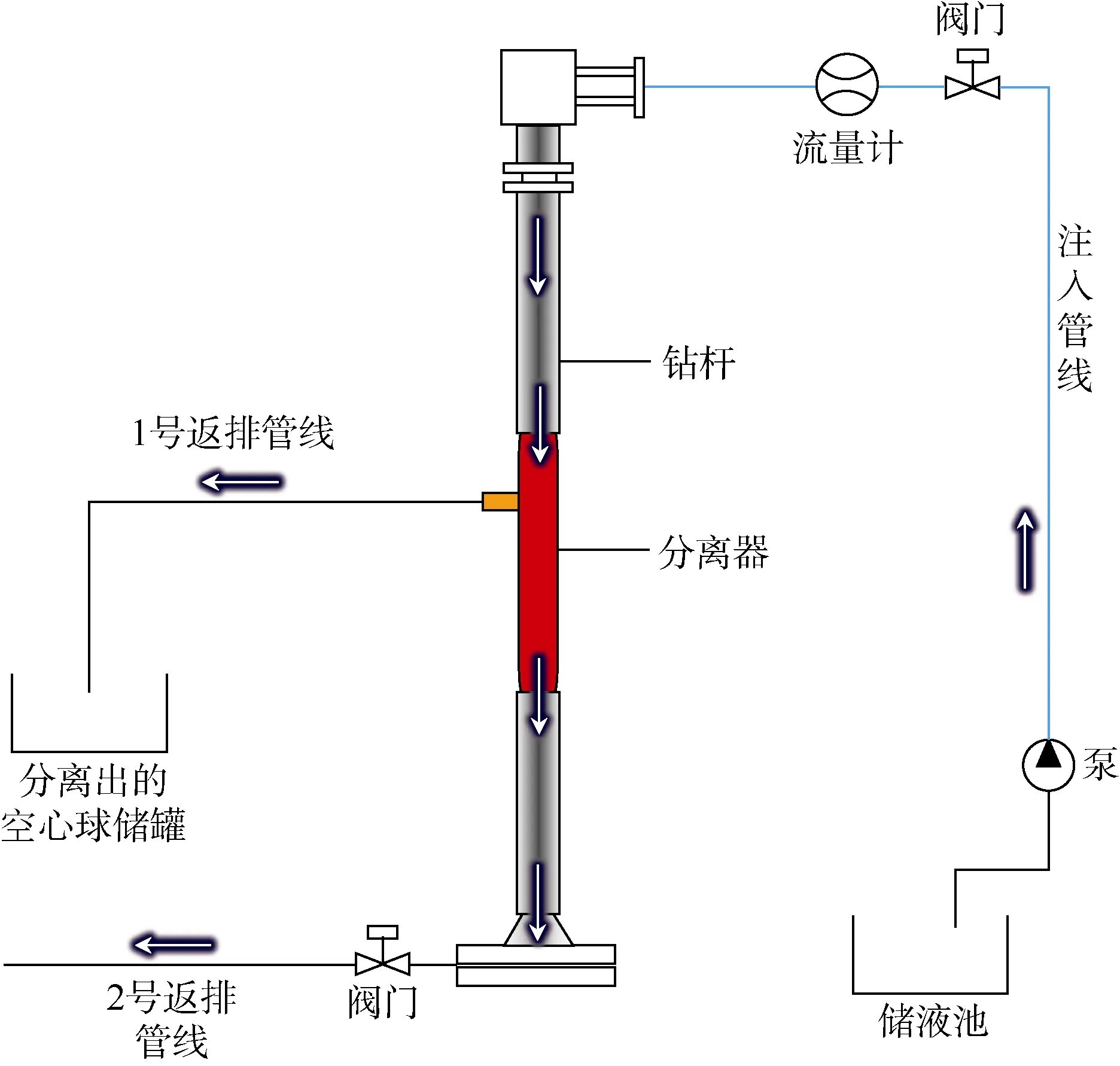
图1 双梯度钻井实验装置

为验证分离器的有效性，开展了室内循环分离实验。进行循环分离实验时，混合流体（以空心球和水为主的混合物）通过泵加压经蓝色注入管线进入钻杆内，经过分离器后部分空心球被分离并从1号返排管线排出，经分离后的混合流体通过底部2号返排管线排出。实验过程中通过测量1号返排管线分离出的空心球与初始加入的空心球质量得到分离器的分离效率，实验结果如表1所示。从空心球分离结果来看，分离器分离效率在40%左右，证明了本研究设计的分离器的有效性。

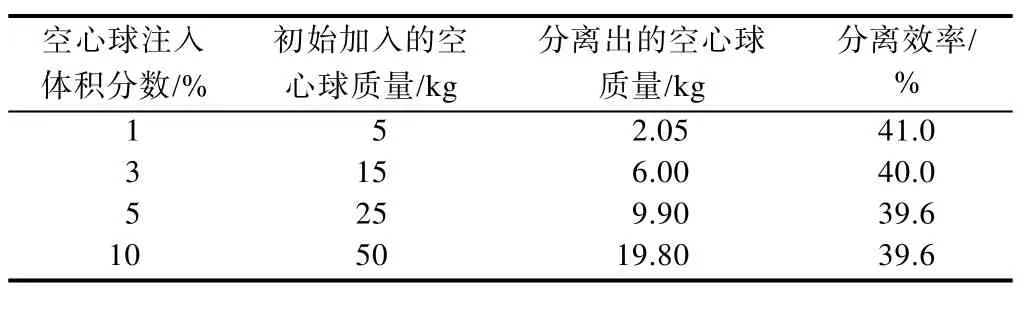
表1 不同空心球注入体积分数下的实验结果

2 钻进过程中动态井筒压力计算

2.1 基本假设

本文进行井筒压力计算时做如下几点假设：①分离效率为常数，取室内实验结果进行实例分析；②不考虑相态变化对井筒压力的影响；③不考虑被分离的空心球进入环空时产生的波动压力。

2.2 数学模型

钻进过程中，由于分离器随井深的增加而下移，使得目标点（指井筒裸眼段内深度相同的任意位置点）处轻质钻井液井段长度增加，而重质钻井液井段长度减小，井筒内轻质、重质钻井液的动态分布导致该井深处井筒压力发生变化，这是常规钻井钻进时井筒压力所不具备的特征（见图2）。由图2a到图2c，井深增加，分离器向下移动，目标点处压力发生变化。

图2 钻进过程中目标点井筒压力组成

对于状态a而言，循环钻井过程中目标点处的压力为：

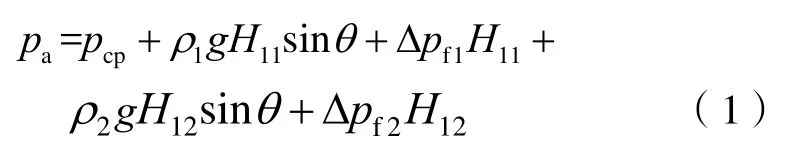
常用的循环压耗计算方法有间接法和直接法[14-15]。间接法通过计算范宁摩阻系数f来求得压耗，f值采用Colebrook公式[16]求取；直接法基于水动力学伯努利方程推导出压耗和各变量间的经验公式。由于利用最优化理论求解优化问题时需要保证井筒压力与变量之间为直接关系式，而不是迭代求解的非线性关系式，所以本研究选择直接法进行循环压耗计算。

按照上述计算方法，可分别获得轻质钻井液和重质钻井液单位长度循环压耗：

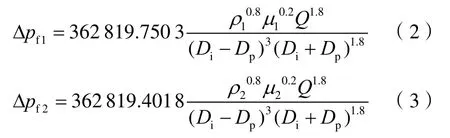
其中

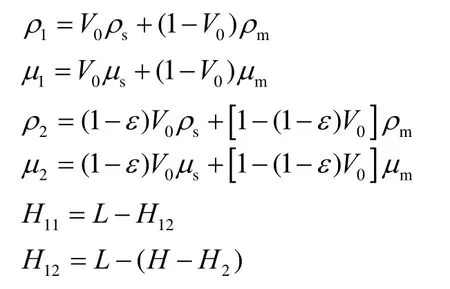
由此建立状态a下井筒内任一点压力与6个变量（分离器分离效率、注入体积分数、纯钻井液密度、分离器与钻头之间的距离、井口回压、排量）之间的关系。对于状态b和c而言，其井筒压力分别为：

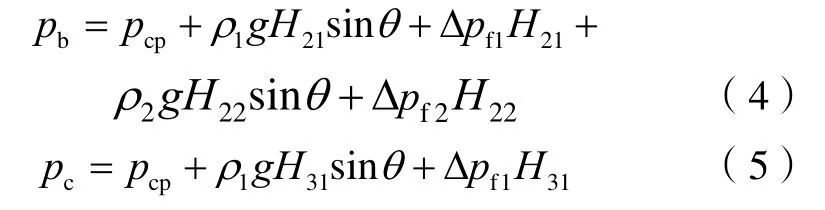
由前述可知，

即循环钻进过程中裸眼段任意点压力随井深变化而变化。所以，研究该钻井方式下的钻井参数优化设计具有重要意义。

3 钻井参数优化设计模型建立与求解

3.1 目标函数

钻井参数优化设计模型的目的是在保证最大钻进深度的前提下，实现最小的井底压差，提高机械钻速。由于无法建立钻进深度与6个变量之间的直接关系，因此将钻进深度作为目标函数在数学上不可行，无法实现优化求解。本文采用当前井深处的井底压差作为目标函数，并将裸眼段任意点的井筒压力和变量取值范围作为约束条件，既实现了井底压差最小化，又保证了最大的钻进井深。最优化模型表示如下：

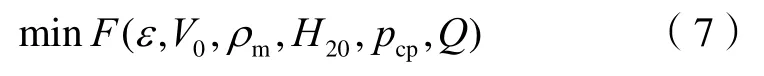
上式中，F（ε，V0，ρm，H20，pcp，Q）为目标函数，定义为当前井深处的井底压差，表达式如下：

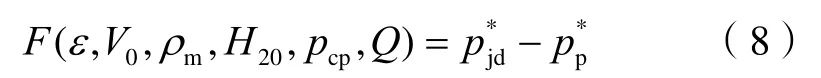
其中

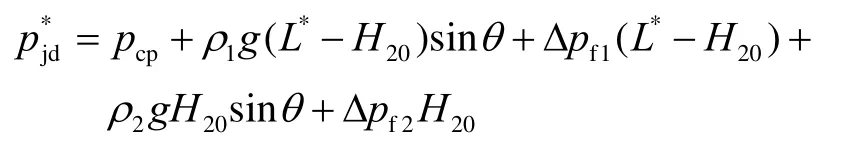
3.2 约束条件

模拟的约束条件如下：

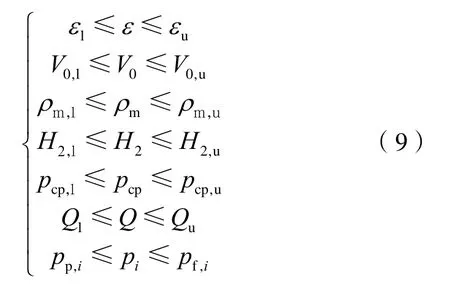
实际钻井中，钻井设备不能完全实时、自动地调节这些参数以达到理想的参数值，因此为了使最优化理论得到的最优变量值在整个单次钻进过程中保持不变，本文将每个变量在取值范围内分为等间隔的n组数据，进行优化计算。n值不宜太大，以防带来数值计算的维数灾问题。

3.3 模型求解

目标函数定义为当前井深处井底压差，在钻进过程中目标函数是动态变化的；另外，随着井深的增加，压力约束条件增多，由于裸眼段任意点的井筒压力是变化的，所以约束条件也呈动态变化。由以上分析可知，该问题是一个有约束的非线性动态最优化问题，将该动态最优化问题分解为有限个静态的有约束非线性最优化问题，利用最优化方法进行求解。

序列二次规划（SQP）方法被认为是解决有约束非线性最优化问题的最有效方法之一[17-18]，该方法在工程方面具有重要的应用价值，本文采用该算法进行模型求解。选取MATLAB中的fmincon函数作为目标函数，调用SQP算法求解原始最优控制问题参数化的非线性规划（NLP）问题。

4 实例分析

模拟井为一口深水直井，基础数据如下：水深1 000 m，已钻井深1 200 m，下套管固井；隔水管外径660.4 mm，内径609.6 mm，钻杆外径127.0 mm，内径101.6 mm，表层套管内径457.2 mm，钻头直径342.9 mm。已知1 200～2 200 m井段的窄安全压力窗口，模拟时设定的极限井深为2 200 m，钻进到该深度时，模拟结束。

4.1 不同控制参数条件下的优化结果

模拟计算时将控制参数（变量）在取值范围内进行等间隔划分，注入体积分数、纯钻井液密度、分离器与钻头之间的距离、井口回压、排量的划分间隔分别为0.02，50 kg/m3，100 m，500 000 Pa，3 L/s。n值越大，参数组数越多，同样间隔条件下变量的取值范围也越大。窄压力窗口为1.03～1.05 g/cm3时，分别取n值为5，6，7进行钻井参数优化设计。不同n值下的变量取值范围见表2，优化结果见表3和图3—图5。

表2 不同n值下的钻井参数取值范围

表3 不同钻井参数取值范围下的优化结果

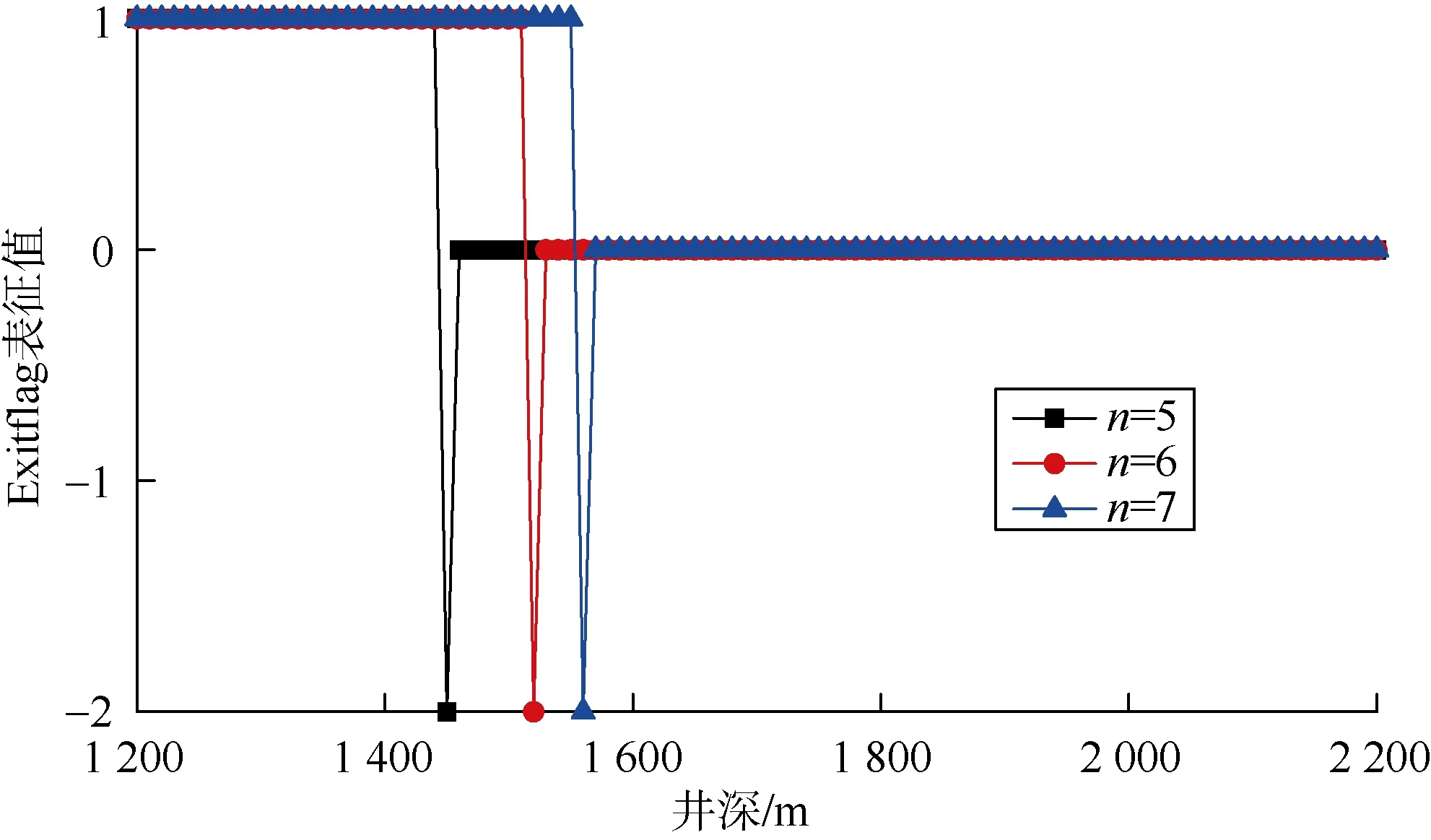
图3 不同变量取值范围下的最大钻进深度表征值

图4 不同变量取值范围下不同井深处钻井液循环压力与孔隙压力的差值

图3给出了不同变量取值范围下的最大钻进深度表征值（Exitflag表征值），约束条件下能够钻达的井深处Exitflag值为1，不能钻达的井深处Exitflag值非1，因此优化时可根据每个深度处的Exitflag值得出约束条件下的最大钻进井深。由表3和图3可以看出，n分别取5，6，7时，最大钻进井深为1 440，1 510，1 550 m。随着n值的增大，变量取值范围变宽，从而可以选取更优的钻井参数，以实现更大的钻进深度。

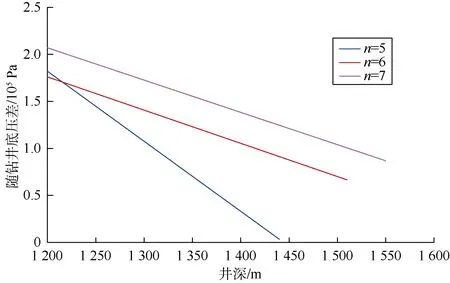
图5 不同变量取值范围下的随钻井底压差

图4给出了不同变量取值范围下的钻井液循环压力与孔隙压力差值，图中虚线表示利用最优钻井参数钻至最大钻进深度时不同井深处的压力差值，图中实线表示已经达到最大钻进深度再继续钻进时不同井深处的压力差值。由图4可以看出，不同的n值条件下，利用最优的变量参数从1 200 m分别钻至对应的最大钻进深度时，裸眼段任意点的钻井液循环压力与孔隙压力差值均大于零，也就是说任意点的井筒压力都在其对应的安全压力窗口内，有效地避免了因压力因素导致的井下复杂情况。当钻井深度超过其对应的最大钻进深度时，井筒内便会出现负压差，部分裸眼井段的钻井液循环压力小于地层孔隙压力，有可能引发井下复杂情况，不利于安全高效钻井。

图5给出了不同变量取值范围下的随钻井底压差，即钻头初次钻至某井深时的井底压差。由图5可以看出，不同n值条件下，利用最优变量值钻进至1 440，1 510，1 550 m过程中裸眼段地层的随钻井底压差值均在2.5×105Pa以下，远小于常规钻井的井底压差值（2.0×106Pa）。最优化设计得到的较小井底压差有利于提高机械钻速，保护储集层，降低钻井综合成本。

4.2 不同窄安全压力窗口条件下的优化结果

在n等于6时，分别取不同的安全压力窗口（1.03～1.04 g/cm3，1.03～1.05 g/cm3，1.03～1.06 g/cm3）进行钻井参数优化设计。优化结果见表4和图6—图8。

表4 不同窄安全压力窗口下的钻井参数优化结果

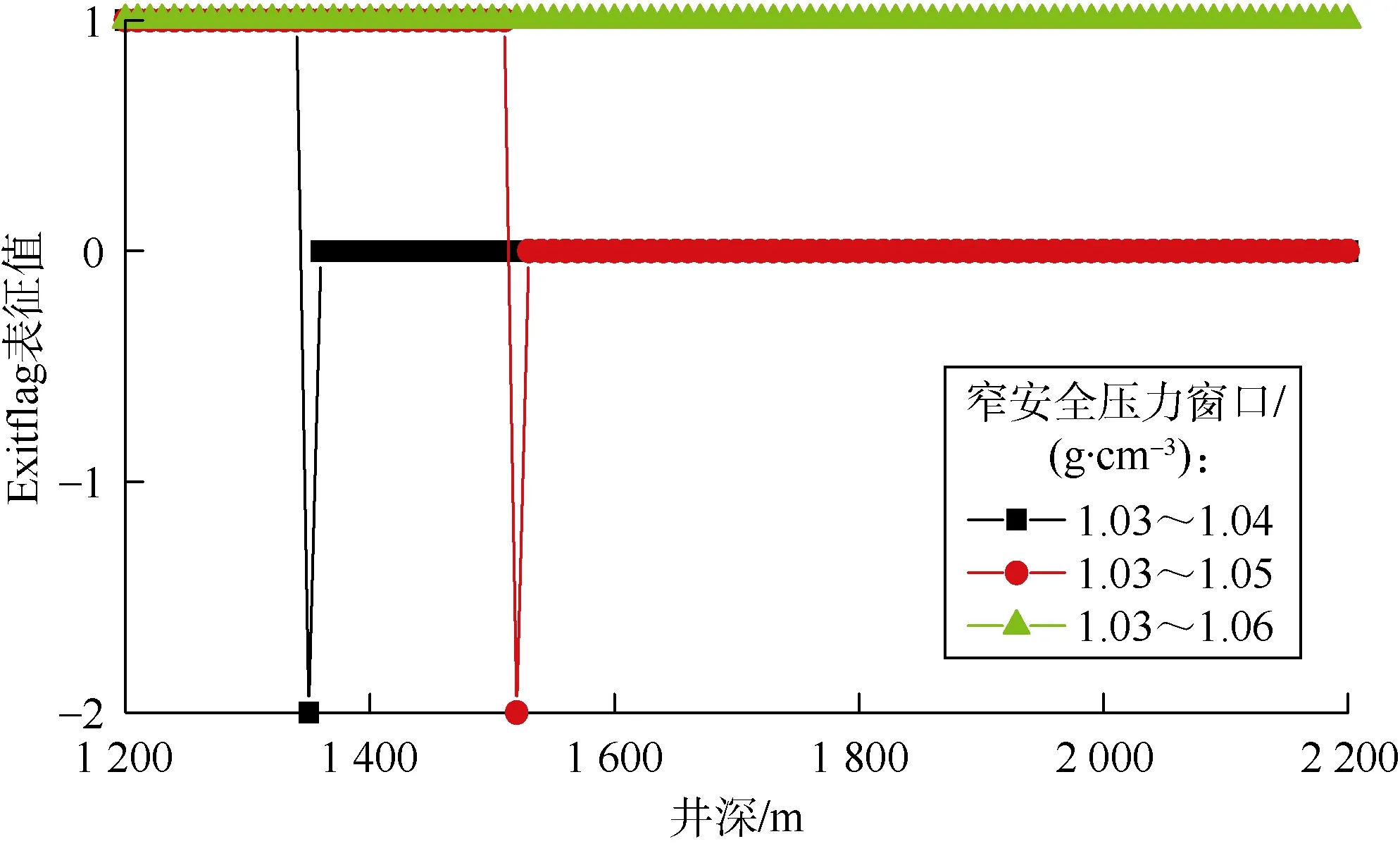
图6 不同窄安全压力窗口下的最大钻进深度表征值

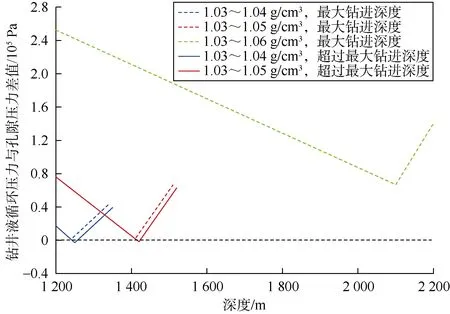
图7 不同窄安全压力窗口下不同井深处钻井液循环压力与孔隙压力的差值

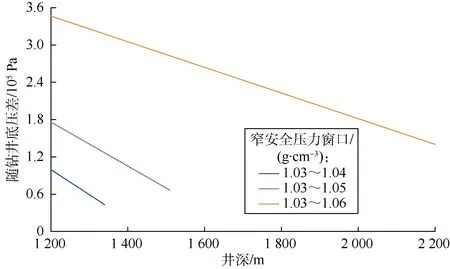
图8 不同窄安全压力窗口下的随钻井底压差

图6给出了不同窄安全压力窗口下的最大钻进深度表征值（Exitflag表征值）。由表4和图6可以看出，地层窄安全压力窗口为1.03～1.04 g/cm3，1.03～1.05 g/cm3，1.03～1.06 g/cm3时，最大钻进井深分别为1 340，1 510，2 200 m。随着安全压力窗口变宽，在同样的压力取值范围内，能够搜索到更优的钻井参数，以实现更大的钻进深度。

图7给出了不同窄安全压力窗口下不同井深处的钻井液循环压力与孔隙压力差值。由图7可以看出，对于不同的压力窗口，利用最优的变量参数从1 200 m分别钻至对应的最大钻进深度时（图中虚线），裸眼段任意点的压力差值均大于零；而当钻井深度超过其对应的最大钻进深度时（图中实线），井筒内便会出现负压差，部分裸眼井段的钻井液循环压力小于地层孔隙压力，可能导致井下复杂情况的发生，不利于安全高效钻井。另外，优化结果表明压力窗口为1.03～1.06 g/cm3时，利用最优变量值可钻至2 200 m（设定的极限井深），因此图中略去压力窗口为1.03～1.06 g/cm3对应的实线图。

图8给出了不同窄安全压力窗口下的随钻井底压差，可以看出，3种压力窗口条件下，利用最优变量值钻进至1 340，1 510，2 200 m过程中裸眼段地层的随钻井底压差值均在3.6×105Pa以下，较小的井底压差有利于提高机械钻速，减小储集层伤害，降低钻井综合成本。

5 结论与建议

室内实验表明在不同空心球注入体积分数条件下，分离器具有较好的分离效果，且分离效率基本恒定，证实了井下分离的有效性和实现井筒双梯度的可行性。优化分离器位置、分离效率等关键控制参数后，达到了优化井筒压力剖面的效果，可更好地适应深水窄压力窗口，实现更大的钻进深度。优化后的随钻井底压差远小于常规钻井的井底压差，有利于提高机械钻速，减小储集层伤害，降低钻井综合成本。本研究主要进行了深水直井条件下的钻井参数优化，建议后续开展深水斜井、水平井等不同井型条件下的钻井参数优化研究。

符号注释：

Di——环空外径，cm；Dp——环空内径，cm；f——范宁摩擦系数；F——目标函数；g——加速度，9.81 m/s2；H——总井深，m；H2——分离器与钻头之间的距离，m；H11——状态a下轻质钻井液段长度，m；H12——状态a下分离器与目标点之间重质钻井液段长度，m；H20——分离器与目标点之间的距离，m；H21——状态b下轻质钻井液段长度，m；H22——状态b下分离器与目标点之间重质钻井液段长度，m；H31——状态c下轻质钻井液段长度，m；L——目标点深度，m；L*——当前井底深度，m；pa——状态a下目标点压力，Pa；pb——状态b下目标点压力，Pa；pc——状态c下目标点压力，Pa；pcp——井口回压，Pa；——当前井深处的地层孔隙压力，Pa；——当前井深处的井底压力，Pa；pi——钻井过程中裸眼段任意位置的井筒压力，Pa；pp——地层压力窗口的下界，即地层孔隙压力，Pa；pf——地层压力窗口的上界，即地层破裂压力，Pa；Q——排量，L/s；V0——空心球注入体积分数；ε——分离器分离效率；θ——井斜角，（°）；μm——纯钻井液塑性黏度，Pa·s；μs——空心球黏度，Pa·s；μ1——轻质钻井液塑性黏度，Pa·s；μ2——重质钻井液塑性黏度，Pa·s；ρm——纯钻井液密度，kg/m3；ρs——空心球密度，kg/m3；ρ1——轻质钻井液密度，kg/m3；ρ2——重质钻井液密度，kg/m3；Δpf1——轻质钻井液段单位长度循环压耗，Pa/m；Δpf2——重质钻井液段单位长度循环压耗，Pa/m。下标：l——最小值；u——最大值；i——不同深度位置。