以抽象函数为背景的不等式问题的破解策略
2019-09-06福建省厦门双十中学梁莹莹
☉福建省厦门双十中学 梁莹莹
一、知识的重要性
抽象函数是指没有给出具体的解析式,只给出一些体现函数性质特征的条件的一类函数,它是高中函数知识模块中非常重要的一种函数类型.在近几年高考和模拟考中,以抽象函数为背景的不等式问题频频亮相,题目以能力立意,短小精干,除考查导数四则运算法则及函数的图像和性质外,重点考查学生分析和解决问题的能力以及创新思维,难度较大,区分度较高,既是热点也是难点.
实际上,根据条件和目标不等式的结构特征,联系导数的四则运算法则和基本初等函数的求导公式,构造新函数,是解决此类问题的关键,这是一种创造性思维过程,具有较大的灵活性和技巧性,如果能掌握相应的构造策略,必能突破问题屏障,提升学生的联系转化的思维能力,锻炼学生的创新思维.
二、学生的困惑
以抽象函数为背景的求解不等式或者比较大小问题,对大部分学生来说既是难点也是薄弱点,主要原因有三:
1.对题目条件中含有导数符号的不等式的结构特征认识不清,对基本初等函数的求导公式和导数的四则运算法则的正向与逆向运算不熟练、不敏感,从而无法构造出新函数.
2.对所求的目标不等式的结构特征分析不到位,或者等价转化的能力不够,无法变形出含有新函数结构特征的式子,导致无法在条件和目标之间产生关联,使得解题受阻.
3.即使能够构造出新函数,但是对新函数的单调性、奇偶性、对称性、特殊的函数值等性质以及图像的综合分析不够全面透彻,导致无法求解不等式.
三、解题策略
1.结构化策略——由局部联想整体,化生为熟
例题1(2015·新课标全国卷Ⅱ·12)设函数f ′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( ).
A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)
C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)
分析:条件不等式同时出现f(x)和f ′(x),两者之间是减号,再联想到(x)′=1,则把条件变形为f ′(x)xf(x)(x)′<0,这恰好符合商的求导法则中的分子结构,逆向应用法则,配凑出分母,等价转化为,因此构造的新函数为
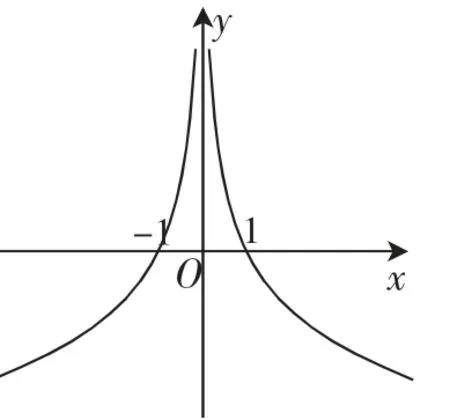
图1
解答:构造函数(x ≠0),则 当x >0 时,在(0,+∞)上单调递减.又因为f(x)为奇函数且y=x也为奇函数,所以F(x)为偶函数,则F(x)在(-∞,0)上单调递增(如图1所示),f(-1)=0⇒F(-1)=F(1)=0.当x>0时,f(x)>0⇒F(x)>0⇒0<x<1,当x<0时,f(x)>0⇒F(x)<0⇒x<-1,故使得f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1),故选A.
【变式1】条件不等式变为xf′(x)+f(x)<0,我们应该构造什么函数?
分析:同时出现f(x)和f′(x),两者之间是加号,再联想到(x)′=1,变形为f′(x)x+f(x)(x)′<0,符合积的求导法则[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x),则f′(x)x+f(x)(x)′=[xf(x)]′<0,因此构造函数F(x)=xf(x).
【变式2】条件不等式变为f′(x)+f(x)<0,我们应该构造什么函数?
分析:同时出现f(x)和f′(x),两者之间是加号,联系积的求导法则,我们需要寻找一个函数g(x),使得它的导函数就是它本身,联想到(ex)′=ex,在f′(x)+f(x)<0的两边同时乘以ex,转化为f′(x)ex+f(x)ex<0⇒[exf(x)]′<0,所以构造函数F(x)=exf(x).
【变式3】条件不等式变为cosxf′(x)-sinxf(x)<0,我们应该构造什么函数?
分析:同时出现f(x)和f′(x),联想到(cosx)′=-sinx,再联系积的求导法则,得cosxf′(x)-sinxf(x)=cosxf′(x)+(cosx)′f(x)=[cosxf(x)]′,所以构造函数F(x)=cosxf(x).
【变式4】条件不等式变为xf′(x)+2f(x)<0,我们应该构造什么函数?
分析:同时出现f(x)和f′(x),两者之间是加号,根据前面的想法,应联系积的求导法则[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x),但是(x)′≠2,法则结构对不上?怎么办?能否对条件不等式进行适当变形,比如说,在不等式的两边同时乘上某个式子,使得结构特征满足积的求导法则?我们需要寻找一个函数g(x),使得,再联系到(x2)′=2x,所以两边同时乘以x(假设x>0),变形出x2f ′(x)+2xf(x)<0⇒[x2f(x)]′<0,所以构造函数F(x)=x2f(x).
【课后思考】条件不等式变为f′(x)-f(x)<0,cosxf′(x)+sinxf(x)<0,xf′(x)-2f(x)<0,应分别构造什么函数?答案:分别构造函数
【总结反思】在题目条件中,总会有一个含有f′(x)符号的式子,其中f(x)是抽象函数,可能还会夹杂一些具体函数形式(比如x,tanx等),联系两个函数四则运算求导法则和基本初等函数求导公式的结构特征,通过移项、同乘或者同除某个具体函数等变形手段,使得局部分散的多个函数的导数关系式,向整体集中的单个函数的导数关系式转化,这个整体函数就是我们所要构造的新函数F(x).
再把待求的目标不等式的两边,等价转化成前面所构造出的新函数结构,根据单调性去掉“F”符号,转化为求解具体不等式,或者根据新函数的单调性比较大小,从而得到答案.
这种策略在填选题和解答题中都适用,是解决此类问题的通法.
2.同构化策略——由结论逆推条件,化异为同
例题2定义在R上的函数f(x)满足f′(x)>f(x),则当a>0时,f(a)与eaf(0)之间的大小关系为( ).
A.f(a)<eaf(0) B.f(a)>eaf(0)
C.f(a)=eaf(0) D.不能确定
解法1:结构化策略(让学生做练习)
先移项变形为f′(x)-f(x)>0,联想到(ex)′=ex和商的求导法则,构造函数,则F(x)在R上单调递增.又因为a>0,所以故选B.
解法2:同构化策略
分析:观察四个选项,除了D选项,A,B,C三个选项结构一致,都是关于f(a)与eaf(0)大小关系的式子,我们尝试移项变形,把具有相同自变量的式子变形到不等式同侧,不同自变量的式子变形到不等式两侧,再联想到e0=1,构造出具有同构性的结构形式,我们把相同的东西保持不动,不同自变量的地方引入变量x,猜想要构造的新函数应为,下同解法1.这就叫“异形同构”,虽然自变量不同,但是不等式两边的结构具有高度一致性,就可以构造这个同构性的函数,再利用新函数单调性来比较大小.
3.特殊化策略——由特殊代替一般,化抽象为具体
例题3已知定义域为R的奇函数y=f(x)的导函数为y=f ′(x),当x≠0时,,则a,b,c的大小关系正确的是( ).
A.a<b<c B.b<c<a C.a<c<b D.c<a<b
分析:不妨设最简单的奇函数f(x)=x对任意的x≠0恒成立,如此a,b,c都可以具体算出来,很容易比较大小.
