四种思维真如铁，平面向量从头越——一道江苏模拟题的破解

☉江苏省太仓高级中学 陈 健

平面向量的考查一直是每年高考、自主招生考试、数学竞赛等试卷的热点问题之一，有时单独考查，有时与其他相关知识交汇与融合考查，是高考中能力齐全、方法多样、思维各异的重要场所.

一、问题呈现

【问题】（江苏省南京市2019届高三二模数学试卷·12）已知AD是直角三角形ABC的斜边BC上的高，点P在DA的延长线上，且满足，若AD=，则的值为______.

二、多解思维

思维角度1

基底法是平面向量的本质所在，是平面向量“几何”化的表现.选用合适的基底，借助平面向量的线性运算，通过极化恒等式或直角三角形的性质加以巧妙转化来求解相应的数量积问题.

解法1：取BC的中点O，结合平面向量的线性运算与数量积公式加以转化得到的长度，结合极化恒等式以及勾股定理加以巧妙转化来求解即可.

设OD=x，OB=y，则有AD2=OA2-OD2=OB2-OD2=y2-x2=2，所以结合极化恒等式可得

故填答案：2.

解法2：通过平面向量的线性运算分别表示出与，借助平面向量的线性运算与数量积公式加以转化得到的长度，结合直角三角形的性质AD2=DB×DC加以转化来求解即可.

故填答案：2.

思维角度2

建系法是平面向量“代数”化的体现，是在可以建系的前提下进行的.建系时往往要借助平面向量中有关垂直向量的关系来处理，以此对应的向量为坐标轴所在的直线.不同的建系会导致不同的效果，经常可以采用不同的方式来处理.

解法1：通过以A点为坐标原点，AB、AC所在的直线分别为x轴、y轴建立平面直角坐标系，进而确定三个内角A，B，C的对边分别为a，b，c，利用题目条件确定对应参数之间的关系，利用直线BC与直线AD的方程来求解点D的坐标，利用平面向量的坐标运算以及数量积公式加以转化得到，再进一步求解即可.

以A点为坐标原点，AB、AC所在的直线分别为x轴、y轴建立平面直角坐标系xAy，

设△ABC的三个内角A，B，C的对边分别为a，b，c，

则有a2=b2+c2，A（0，0），B（c，0），C（0，b）.

图1

由于AD是直角三角形ABC的斜边BC上的高，则直线AD的方程为

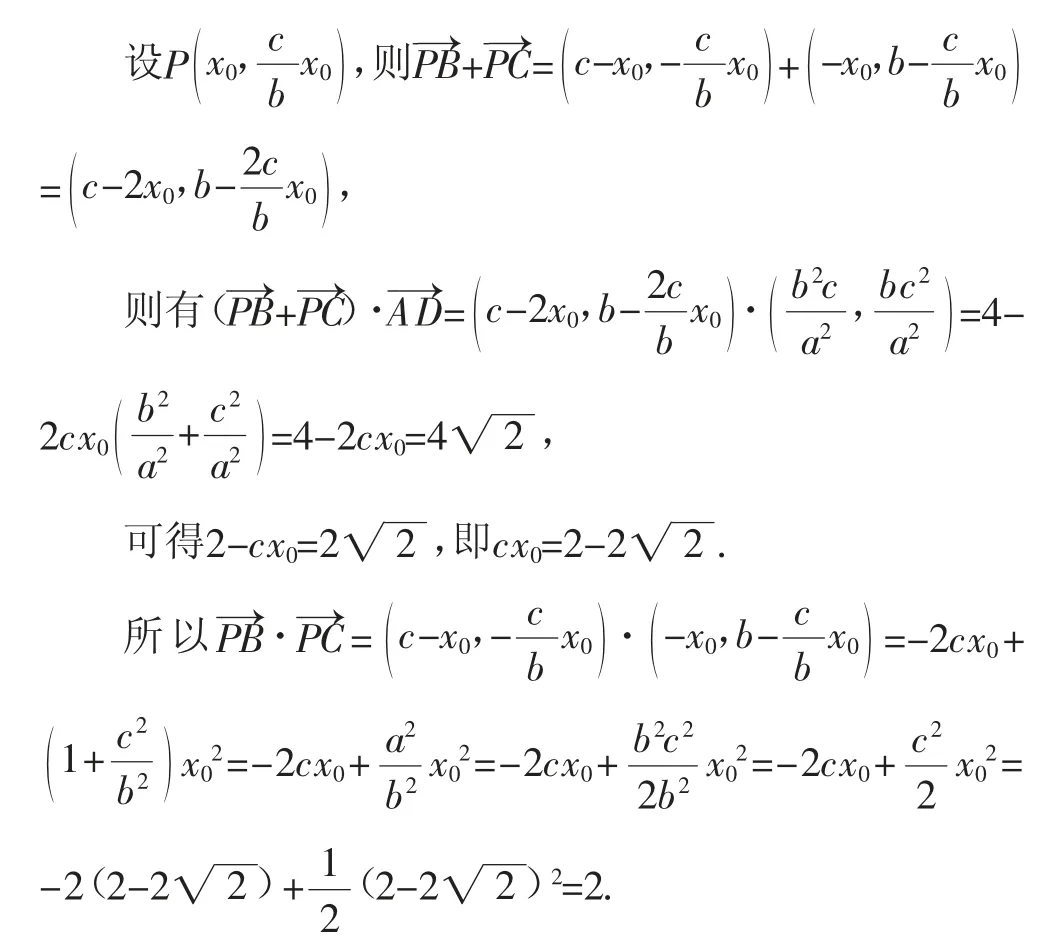
故填答案：2.

思维角度3

三角函数法是平面向量问题在三角形中的具体展示，是平面向量问题向直角三角形回归的充分体现.借助三角函数的定义、三角恒等变换公式等，结合平面向量的数量积公式等加以有效转化与求解.

解法1：引入∠DPC=α，∠DPB=β，结合条件，利用平面向量的数量积公式、直角三角形中三角函数的定义等加以转化得到PD=2，再次利用平面向量的数量积公式，结合三角恒等变换公式，以及直角三角形中三角函数的定义等，通过直角三角形的性质AD2=DB×DC的转化来求解即可.

设∠DPC=α，∠DPB=β，

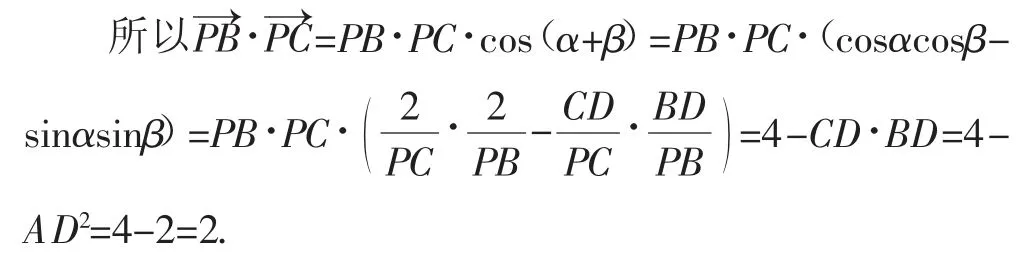
故填答案：2.

思维角度4

特殊图形法是解决具有定值结论的平面向量问题的一种技巧方法.结合题目条件，通过构造特殊的平面几何图形（特别是三角形、平行四边形等），利用特殊的平面几何图形的特点，结合向量运算的几何意义（三角形法则或平行四边形法则等）来分析与求解，往往可以使解题更直观，更简捷，便于判断与操作.

解法1：构造等腰直角三角形ABC，利用等腰直角三角形的性质得到斜边BC的中点也是D，根据条件AD=，利用数量积的转化得到，通过勾股定理与余弦定理的转化，利用平面向量的数量积公式来求解即可.

图2

构造等腰直角三角形ABC，此时斜边BC的中点也是D，

故填答案：2.

三、规律总结

平面向量既有“数”的因素，又有“形”的思维，既是几何的，可以画图；又是代数的，可以运算.因此平面向量的破解往往可以从“数”与“形”的“两面性”思维来考虑，通过建系法或三角函数法以“数”的形式来破解，通过基底法或特殊图形法以“形”的形式来破解，各有各的好，各有各的妙.所以，在平面向量中，充分提高平面向量的识“图”、用“图”能力，拓展平面向量的用“数”、解“数”思维，可以非常有效地从“数”的方面或从“形”的方面加以平面向量的“两面性”思维，达到多角度思维、多方法处理的效果.