一种基于快速增量序列挖掘的短波频谱预测方法*

赵伟敏 ，程云鹏 ，赵越超

（1. 陆军工程大学 通信工程学院，江苏 南京210007；2. 中国人民解放军61932部队，北京100071）

0 引 言

研究频谱特性是有效利用频率资源的前提。短波频谱持续快速变化，抓住并利用其频谱机会是各国机构普遍关心的课题[1]。频谱预测（Spectrum Prediction）能够从历史频谱数据中捕捉频谱状态变化规律，推断频谱的未来状态，提供有益的用频建议。数据挖掘就是一类通用性强且性能较好的频谱预测方法[2]，以此能够较好利用频谱机会。

序列模式挖掘[3-10]（Sequence Pattern Mining，SPM）是数据挖掘方法的一种，适合挖掘具有时态次序的数据模式。然而不足在于，类Apriori算法[3]产生大量候选序列且需多次扫描数据库；SPADE算法[4]需构造并存储垂直序列；基于投影的算法[5-6]构造存储投影数据库导致占用较多内存；文献[7]设计了简化频繁模式挖掘（Simplified Frequent Pattern Mining，S-FPM）算法用于短波频谱预测，但只考虑静态数据库下的单次挖掘，数据动态更新时效率较低；增量序列挖掘（Incremental Sequential Pattern Mining，ISPM）算法[8-10]能够用于动态更新数据，但存在和对应的非增量算法同样的局限。

针对以上不足并结合实用需要，本文提出一种基于快速增量序列挖掘的短波频谱预测方法，核心思想是在ISPM基础上，依据序列长度覆盖率（Sequence Length Coverage，SLC）指标优化序列长度集，从而快速预测频谱。该方法特点在于：（1）算法运行开销减少，结合本地频谱特点，精简候选序列；（2）频谱数据库使用效率提高，利用已挖掘知识加快当前挖掘过程。

本文结构如下：第1节构建了频谱可用性模型，第2节提出了基于增量序列挖掘的频谱预测方法，第3节介绍了搭设的频谱测量系统，第4节进行了算法仿真与分析，最后总结全文工作。

1 频谱可用性模型

1.1 频谱状态划分

认知无线电（Cognitive Radio，CR）划分频谱状态的一般方法是将信号接收功率按能量检测法划分为占用/非占用状态[11]，即

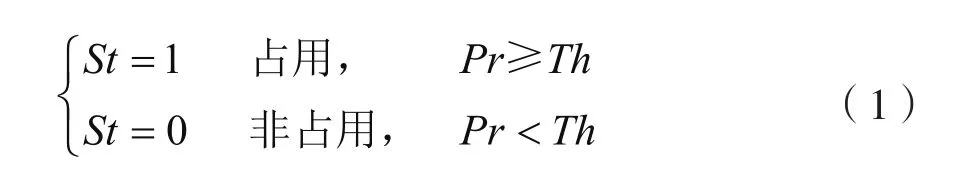
其中，Pr表示信号接收功率，Th为能量检测阈值。

短波频段宽不足30 MHz，频谱质量动态变化，但各功率峰间往往存在着功率较低且持续一定时间的窄带，这种窄带可称为频谱机会。

为更好地反映频谱质量变化，对上述划分方法进行改进：

（1）按适当小的频宽F、时长T提取频谱数据作为基本分析频带，对各频带设置不同的能量检测阈值，如图1所示。

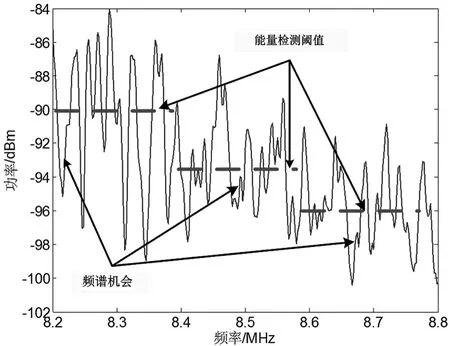
图1 各频带设置不同能量检测阈值

（2）按频率间隔df、测量时隙dt分析频谱数据，对接收功率做M状态均匀量化（M为量化阶数），得到频谱状态St∈{0,1,…,M-1}及频谱机会，如图2所示。

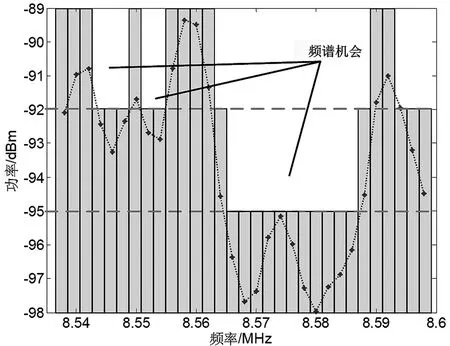
图2 M状态均匀量化的频谱机会（M=3）

1.2 频谱可用性建模

可用性建模通常是将占用状态数的百分比计作频谱占用度[12]，从统计意义上反映频谱可用程度，缺点是不能保证实际频谱可用是时间连续的。

考虑频率切换所需时间大于测量时隙，取同一频点的连续n个时隙为预测单位时间，记作时间元τ。如图3，依据时间元τ内频谱状态的优劣程度，区分三状态可定义必要的频谱可用性，

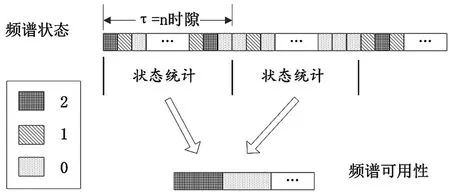
图3 单频点的频谱可用性统计

由频谱状态数据得到可用性数据，频带内总频点数fm=F/df，总时间元数tm=T/dt/n。于是有频点m第t个时间元的频谱可用性其中t∈{1,2,…,tm}，m∈{1,2,…,fm}，从而全部频点第t个时间元以前的频谱可用性矩阵为

该可用性模型给出了三状态可用性的严格区分，经预测能直接得到频谱可用建议；时间元τ较小时，调整≤≤取值能够约束频谱状态序列，使连续时间内不出现恶劣的频谱状态，避免“可用”频率发生未知中断。图4为τ=3时隙的建模结果。

图4 当τ=3时隙的频谱可用性

2 基于增量序列挖掘的频谱预测方法

2.1 设计思想

该预测方法通过SLC指标精简序列长度集，然后对频谱数据库实施增量挖掘，最终利用挖掘结果预测频谱，其核心算法是基于序列长度覆盖率的增量序列挖掘（Sequence Length Coverage-Incremental Sequential Pattern Mining，SLC-ISPM）。下面借用序列频繁、序列包含、支持数等概念定义[8]，说明预测方法的主要环节。

（1）利用SLC指标确定序列长度

短波频谱快速变化，而可用性状态是有限重复的，即频繁序列数量有限，因此可考虑精简序列集。定义序列长度覆盖率（SLC）是由候选序列得到同样长度频繁序列的数量比，

其中，k为序列长度，k∈N+且k≥2，NkS、NkC分别为序列长度为k时频繁序列和候选序列的数量。

SLC指标反映了增量序列挖掘过程由候选序列提取频繁序列而减少内存占用的程度。序列数量越小，存放序列信息的内存开销越小；序列长度覆盖率越小，运行过程释放内存越多。

（2）挖掘长度为k的新频繁序列

合并原数据库和新增数据形成新频谱数据库，通过增量挖掘得到新频繁序列，包括：

①原频繁序列在新增数据中仍频繁的部分；

②新增频繁序列在原数据库也频繁的部分；

③原数据与新增数据合并位置的频繁序列。

（3）生成长度为k+1的候选序列

由长度为k的新频繁序列生成长度k+1的候选序列，从中剔除子序列非频繁或本身重复的序列。返回第（2）步，重复该过程，直到发现所有序列长度的新频繁序列。

（4）依据挖掘结果进行预测

挖掘得到频繁序列及支持数信息，根据“序列支持数越大，序列出现概率越大”原则，支持数最大的序列末项就是最大出现概率的频谱可用状态。

2.2 增量挖掘过程

以频谱数据库为例，说明增量序列挖掘过程。首先明确基本符号含义，见表1。

下面为增量挖掘更新知识的过程，输入项已知或已挖掘可知，输出项是新频繁序列集：

输出：S´k；

4：剔除无效或重复的候选序列sk和ck；

7：对数据库db扫描Ck得到

10：end for。

表1 预测过程的符号定义

2.3 频谱预测过程

利用挖掘结果预测频谱的依据是，序列挖掘将原频谱数据的统计信息压缩为频繁序列，于是支持数大的序列出现概率大。已知频点m第t个时间元的数据由已挖掘知识推断第t+1个时间元的可用性

以上过程可获得单个频点的预测结果，逐频点预测最终得到下一时间元全部频点的可用状态

2.4 算法分析

本文通过SLC-ISPM算法预测频谱，并引入简化频繁模式挖掘算法[7]（S-FPM）、隐马尔科夫模型[13]（Hidden Markov Model，HMM）和三层BP神经网络[14]（Back Propagation Neural Network，BPNN）作为比较，现从运算复杂度和内存开销两方面分析算法。

为表述清楚，将必要的算法参量明确如下：设频谱数据长度为n，于是HMM输入数据长度为n，BPNN训练样本数也为n且每个样本训练一次。算法复杂度分析的化简结果见表2。

表2 算法复杂度分析结果

由表2看出，SLC-ISPM、S-FPM和BPNN的运算复杂度均为O(n)，而HMM的运算复杂度为O(n2)，相较之下SLC-ISPM复杂度相对最小；内存开销上，SLC-ISPM算法的开销同样较小。

3 频谱测量系统设计

为验证所提出频谱预测方法的真实性能，自主搭设频谱测量系统采集短波频谱数据，如图5所示。

图5 频谱测量系统的结构示意

选用Keysight N9020B频谱分析仪与鞭状天线接收测量短波频段本地信号功率，编写LabVIEW程序作为频谱仪控制测量平台。表3列出部分测量参数，数据存储为T×F的矩阵形式。测量与存储过程可能发生数据错漏，仿真前需进行相应的预处理。

表3 短波频谱测量参数

4 算法仿真与分析

4.1 参数设置优化

仿真环境配置：处理器Core i7-7700@3.6GHz，内存8GB，操作系统Windows 7 SP1 x64，仿真平台MATLAB R2010b x64。为统一评价算法性能，明确仿真参数如下：以9～9.3 MHz频谱数据进行仿真，取时长T=500τ，时间元τ=10时隙，频谱状态St∈{0,1,2}，频谱可用性U∈{0,1,2}。取前70%时隙的数据用于频谱预测，余下30%时隙用作结果校验。

依据SLC指标精简序列长度，目标是保持预测性能不明显下降的同时，使序列数量少且序列长度覆盖率小。令支持度minsup=0.01，计算不同序列长度下的序列长度覆盖率及序列挖掘算法性能（以S-FPM算法计算），如图6与图7所示。

由图6看出，序列长度k=2→5时，序列长度覆盖率快速下降，候选序列相对较少；而由图7发现序列长度k=2～3时，算法预测准确性能均较好，综合确定序列长k=3。当支持度为0.03、0.05时，可验证k=3仍是最优选择。

图6 不同序列长度下的覆盖率及序列数量

图7 不同序列长度下的序列挖掘算法性能

4.2 不同预测时长的性能

基于17:00～19:00频谱可用性数据连续预测多步，固定样本量T=350τ，计算不同预测时长下四种算法的预测准确率，如图8所示。预测步长为τ，最大预测30步，求200个频点平均性能。

由图8看出，SLC-ISPM和S-FPM算法的预测准确率相等；SLC-ISPM的准确率稍小于HMM算法和BPNN模型但差值很小；在最大预测步长内，准确率未随预测时长增加而出现明显下降。

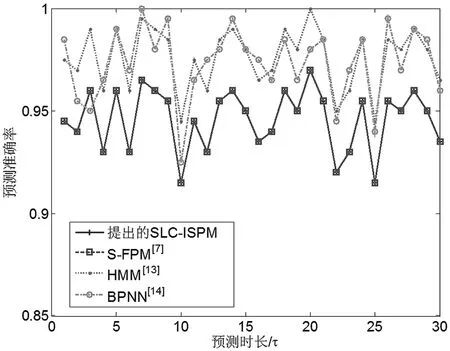
图8 不同预测时长下的准确率

4.3 不同样本时长的性能

用相同数据进行单步预测仿真，取最大样本时长T=500τ，计算不同样本量下预测200个频点的平均性能，如图9、图10所示。由图9看出，增加样本量能提高所有算法的准确率，明显能使BPNN模型收敛；SLC-ISPM算法的准确率略小于HMM算法但优于S-FPM算法，且准确率波动远小于BPNN模型。由图10看出，SLC-ISPM和S-FPM算法始终未漏警，而BPNN模型和HMM算法在样本量较小时更容易发生漏警错误，增加样本量可使后两种算法的漏警率收敛。

图9 不同样本时长下的准确率

图10 不同样本时长下的漏警率

4.4 不同数据增量比例的算法耗时

由表2发现，SLC-ISPM算法的运算复杂度小于S-FPM算法，但属于同一量级。考虑进一步仿真比较，在同一仿真环境下不同时运行其它程序，采用相同数据预测仿真，计算不同数据增量比例下的SLC-ISPM算法与S-FPM算法的运行耗时。图11记录了200个频点预测时长3τ时单频点的平均耗时。由图11发现，不同数据增量比例下SLC-ISPM算法的运行耗时均小于S-FPM算法；随数据增量比例增加，SLC-ISPM算法能节约更多运行时间，仿真结果与理论分析相符。

图11 不同数据增量比例下的算法耗时

5 结 语

本文针对实际预测场景下频谱数据库持续增量更新的特点，提出了一种基于快速增量序列挖掘的短波频谱预测方法。该方法建立三状态频谱可用性模型，设计了SLC指标合理舍弃了完备序列模式，并将增量序列挖掘思想引入频谱预测，提高了频谱数据库利用效率。理论分析和实测数据仿真表明，相比常见预测算法，该方法在保持较好预测性能的同时，显著减少了运算复杂度和内存开销。本方法是单时隙预测方式，为了提高算法效率并改善实用性，下一步需考虑增量更新情况下的多时隙预测方式。