一类最优汉明相关性能的跳频序列集*
2019-09-04段梦军
刘 方 ,刘 捷 ,段梦军
(1.网络空间安全四川省重点实验室,四川 成都 610041;2.中国电子科技网络信息安全有限公司,四川 成都 610041;3.西南交通大学 信息科学与技术学院,四川 成都 610030)
0 引 言
跳频(FH)多址扩频系统具有抗干扰性、抗截获以及抗接入的能力,因而在军事无线电通信、移动通信、多用户雷达和声呐系统等工程中得到了大量应用。在跳频通信系统中,地址分配必须满足发送者和其发送的信息没有模糊性,并且接收信号之间尽可能减小相互干扰。跳频多址通信中的相互干扰主要是受跳频序列之间的汉明相关性能所影响,因此需要寻找同时具有低汉明相关和序列集合容量大的跳频序列集。另一方面,为了抗干扰和抗截获,具有大线性复杂度的跳频序列也是人们所关注的。
目前,在跳频序列设计的理论界方面,人们已经取得了许多成果,诸如Lempel- Greenberger界[1]、Peng-Fan界[2]等。在最优跳频序列集设计方面,利用代数和组合工具[3-9],人们设计了很多多具有优良汉明相关性能的跳频序列集。同时,利用理想自相关特性的p元伪随机序列,人们构造了很多具有最优汉明相关特性的跳频序列。刘元慧等人[10]利用m序列构造了一类具有新参数的最优跳频序列集,基于纠错码人们也构造了一些最优跳频序列集[11-13]。
1 基本概念
设一个跳频多址通信系统具有q个频点,频点集合为F={f1,f2,…,fq}。S表示一个基于频点集F上的跳频序列集合,包含M个跳频序列,每个序列长度为L。
给定S中的任意两个跳频序列X={x0,x1,…,xL-1}和Y={y0,y1,…,yL-1},在相对时延为τ时,它们之间的周期汉明互相关定义为
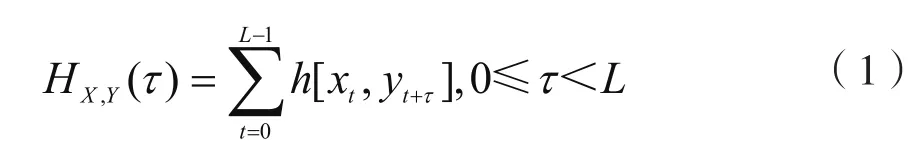
下标t+τ按模L运算,h[xt,yt+τ]表示:
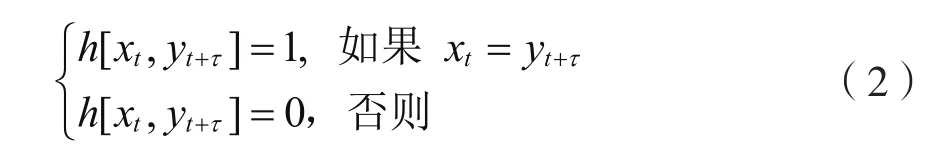
当X=Y时,HX,Y(τ)称为汉明自相关函数。
针对跳频序列集S,下面给出最大汉明相关函数Hmax(S)的定义:
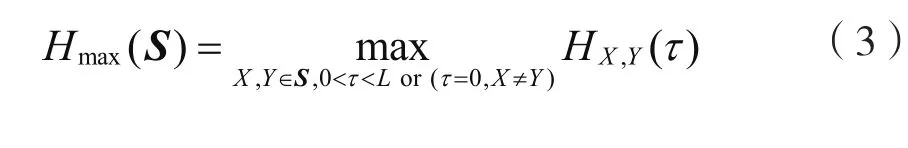
1974年,Lempel和Greenberger首次构建了针对单个跳频序列或一对跳频序列的最大汉明相关值满足的界,即M=1或2。
引理1(Lempel-Greenberger界)[1]对于一个长度为L,频点个数为q的跳频序列X,其最大汉明自相关值满足如下关系:

其中,b表示L除以q的最小非负余数。
后来,Peng和Fan对Lempel-Greenberger界进行了扩展,给出了跳频序列集的最大汉明相关值满足的界。
引理2(Peng-Fan界)[2]对于一个跳频序列集S,其频点集大小为q,序列数目为M,序列长度为L,设那么:
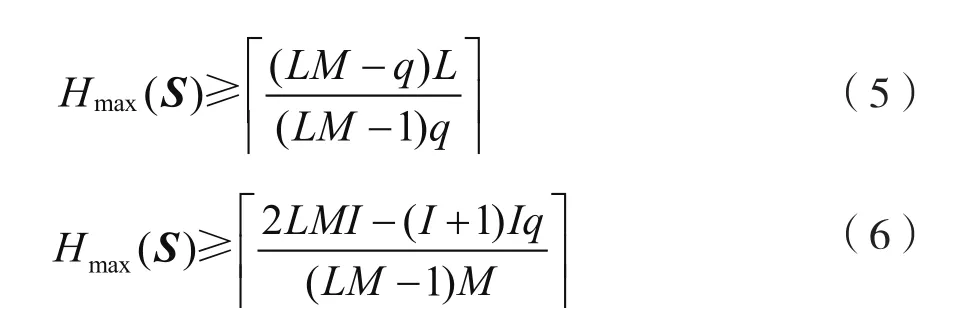
基于引理2中给出的跳频序列集的最大汉明相关值满足的界,下面我们给出最优跳频序列和最优跳频序列集的定义。
定义1 如果一个长度为L,频点数为q,最大汉明自相关值为Λ的序列X的参数使得式(4)的等式成立,则称X是一个最优的(L,q,Λ)跳频序列;针对一个序列个数为M,序列长度为L,频点数为q的跳频序列集S,如果其参数使得式(5)或(6)的等式成立,那么称S是一个最优的(L,M,λ;q)跳频序列集,其中λ=Hmax(S)。
2 d-型函数
令q为一个素数p的n次幂,Fqn表示具有qn个元素的有限域,由文献[14],我们可以得到如下引理和定义。
引理3[14]令是Fq上的非平凡加法特征,对任意的得到
定义2 若f(x):Fqn→Fq的自相关函数满足下式:
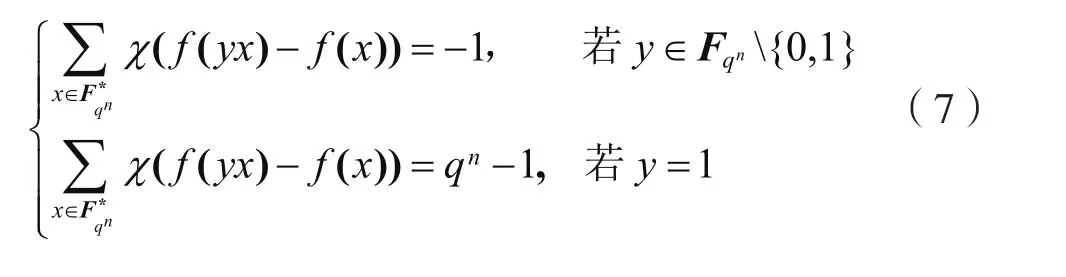
则称函数f(x)具有理想自相关性。
定义3 设d表示一个正整数且满足gcd(d,qm-1)=1,f(x)是从Fqn到Fqm的一个函数。那么对任意的λ∈Fqm,x∈Fqn,如果有

那么称f(x)是一个d-型函数。
在q>2的情况,目前存在三种从Fqn映射到Fq且具有理想自相关性的d-型函数[15-16]:
(1)ρ(x)表示一个迹函数,即:
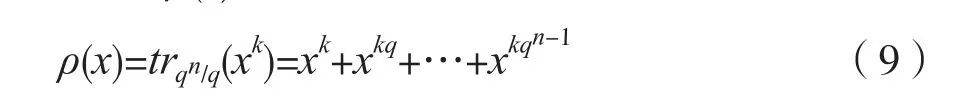
其中k为一个正整数且满足gcd(k,qn-1)=1。
(2)h(x)为Helleseth-Gong(HG)函数,其定义为:

其中,n=(2m+1)e,1≤s≤2m是一个正整数且满足gcd(s,2m+1)=1,b0=1,bis=(-1)i,bi=b2m+1-i,i=1,2,…,m,γ0=b0/2=(p+1)/2,γi=b2i。
(3)g(x)为ρ(x)和h(x)的复合函数,如:

其中,n1,n2(2m+1)e,k1,k2均为正整数,gcd(k2,qn1-1)=1,gcd(k2,qn1·n2-1)=1。
由定义2,可以看出式(9)中的ρ(x)是k-型函数,式(10)中的h(x)是1-型函数,g1(x)是(k1·k2)-型函数,g2(x)为k1-型函数。
3 基于幂函数及具有理想自相关特性的d-型函数构造跳频序列集
下面给出基于幂函数及具有理想自相关特性的d-型函数构造跳频序列集的方法,得到了一类具有最优汉明相关的跳频序列集。首先给出一些后面频繁使用的概念和符号。
α表示F*qn的生成元,T=(qn-1)/(q-1)。
χ表示Fq的非平凡加法特征。
f(x)表示从Fqn到Fq的d-型函数且具有理想自相关特性。不失一般性,令f(x)为1-型函数,即对于任意的y∈Fq,x∈Fqn,f(yx)=yf(x)。
设r是一个正整数,N=gcd(r,qn-1)。对于每一个0≤i<N,构造如下跳频序列:
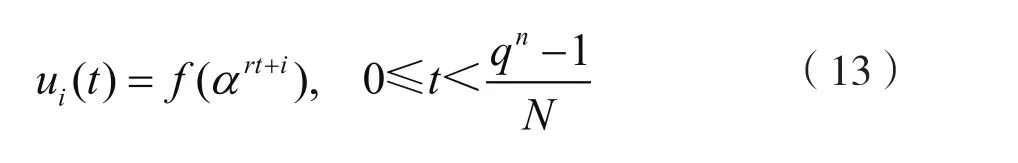
那么,ui为Fq上长度为(qn-1)/N的序列。
定义一个跳频序列集U:

定理 1 设N=gcd(r,qn-1)是一个正整数,且满足gcd(N,T)=1。那么U是一个跳频序列集,且关于引理2的Peng-Fan界是最优的。式(10)中定义的每个跳频序列关于引理1的Lempel-Greenberger界是最优的跳频序列。
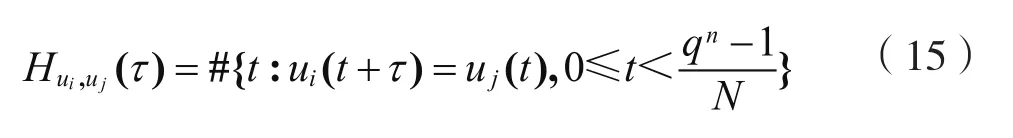
由引理3和函数f的1-型性质,得到:

其中,y=αrτ。
通过上述分析,ui和uj之间的汉明相关函数为:

其中,δ=αiy/α j。
当i=j且0<τ<(qn-1)/N时,我们有δ≠1。根据f(x)的理想自相关特性,有:
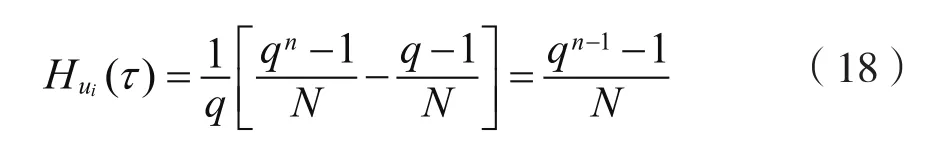
当i≠j且0≤τ<(qn-1)/N时,有δ≠1。同样地,我们得到:
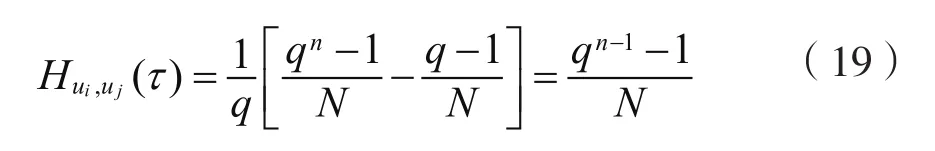
当i=j且τ=0时, 平 凡 汉 明 相 关 值 为Hui(0)=(qn-1)/N。
综上所述,U是一个跳频序列集,其中的每个序列是跳频序列。根据最优跳频序列集的定义,可以验证U关于Peng-Fan界为最优的跳频序列集,其中每个序列关于Lempel-Greenberger界是最优的跳频序列。
注 1 令f(x)=trqn/q(x),那么得到:
当N=2时,U即为文献[8]中第III节所得到的序列集。U中每个序列的线性复杂度为n,其中q和n均为奇数;
当N=q-1时,U即为文献[17]中第IV节所得到的序列集。其中每个序列的线性复杂度为n;
对任意整数N满足N|(q-1)和gcd(N,T)=1,U即是文献[6]中第IV节所得到的跳频序列集。U中每个序列的线性复杂度为n。
如果我们采用其它具有理想自相关性质的d-型函数,那么就可以得到具有更大线性复杂度的最优跳频序列集。
推论 1 令f(x)是式(10)所定义的HG函数,则式(14)定义的跳频序列集U为一个最优的跳频序列集。U中每个序列关于Lempel-Greenberger界是最优的,且线性复杂度为(m+1)n。
4 结 语
本文基于幂函数和具有理想自相关特征的d-型函数构造了一类跳频序列集,利用d-型函数特性证明了所构造的跳频序列的汉明相关特性满足Peng-Fan界和Lempel-Greenberger界,是一类最优的跳频序列集。同时,通过采用HG函数,本文的构造方法能够得到具有更大线性复杂度的最优跳频序列集,这些序列集在军事跳频通信系统中具有广阔的应用前景。
