信噪比的不同定义及对调制识别性能评估的影响*

石 荣，吴 聪

（电子信息控制重点实验室，四川 成都 610036）

0 引 言

无论是对测量条件的描述，还是对参数性能的评估，信噪比（Signal-to-Noise Ratio，SNR）这一概念在导航[1]、通信[2]、雷达[3]、电子战[4]等工程中广泛使用，例如：在各种SNR条件下开展不同试验方法的对比，以衡量不同方法的优劣，SNR为此提供了统一的度量尺度[5-6]，从而也间接助推了工程技术的不断向前发展。从广义上讲，信噪比是指一个电子设备或电子系统中信号与噪声的比例[7]。在这一原生态的定义中并没有明确指出采用哪一种物理量来对信号与噪声进行度量，以及如何进行度量，所以不同的SNR定义和度量方法会引出不同的衡量尺度，也就自然会造成对同一个试验结果给出不同的评价结论。如果在使用SNR这一概念时不明确给出其在当前应用中的定义说明和度量方法，往往会造成数据分析的混乱和实验结论的偏差，给结果评价造成误解，甚至导致谬误的发生。

针对这一问题，本文对信噪比这一概念进行了解析，对工程中各种常用的不同SNR定义，分析了其主要应用场合、以及它们之间的区别与联系，指出了在工程应用中使用SNR概念时一定要明确说明其定义及度量条件的必要性。另一方面，以工程中的信号积累与调制识别等应用为例，分析了不同的SNR度量对此类工程测量的影响，揭示了理论与工程之间存在的现实差异，以及不同SNR对测量条件的不同限定，从而为广大工程技术人员更好地理解与使用SNR这一度量尺度提供了重要参考。

1 两种不同的功率信噪比

通常情况下，信噪比默认定义为信号功率S（单位：W）与噪声功率N（单位：W）之比，记为即大家熟知的功率信噪比，这也是最常见的一种信噪比定义。但在该定义中并没有给出噪声功率的测量条件，从而造成在使用这一概念时产生了混乱。

众所周知，微波接收机中单位带宽内的噪声功率是一个由接收机噪声系数、外界环境温度等多种因素所共同决定的一个确定值，记为n0（单位：W/Hz=J）。如果在功率信噪比测量过程中噪声的带宽为Bn（单位：Hz），信号的带宽为Bs（单位：Hz），则有下式成立：

由此可见：给定一个被测信号，其带宽Bs也随之确定，但噪声带宽Bn在满足式（2）的条件下，在理论上可任意取值，当然在工程应用中其取值范围会受到接收机瞬时接收带宽参数的限制。由式（3）可知：如果在使用功率信噪比时不明确给出准确数值，就会造成之间没有明确的对应关系，从而给工程应用中的性能度量与评估带来混乱。举例说明如下：一个BPSK调制的数字通信信号的传输速率为0.8 Ms/s，采用升余弦成型滤波器形成单个符号波形，滚降系数为0.25，于是该信号带宽Bs=1 MHz，假设其功率S=10-12W；与信号在同一测量点处的接收机噪声功率谱密度n0=10-19W/Hz，显然该信号的带内功率信噪比（对应10dB）。但在不同噪声带宽Bn取值条件下该信号的全频段功率信噪比表1中第2列所示，所对应的dB值如表1中第3列所示。

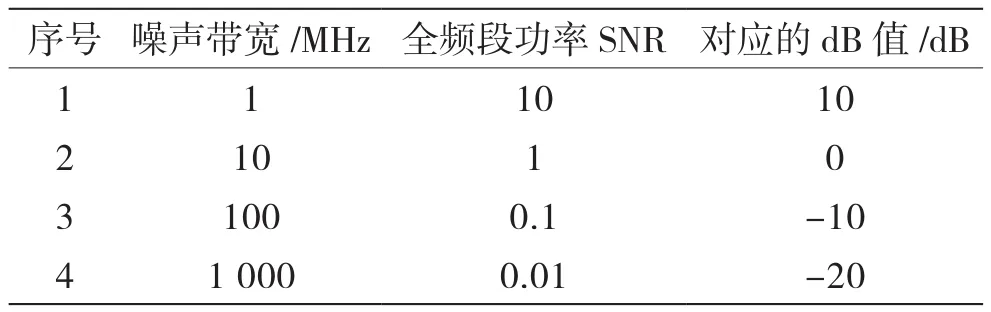
表1 不同噪声带宽取值条件下的全频段功率信噪比

另一方面，特别是近二十多年以来，许多研究者常常使用MATLAB软件中高斯白噪声产生函数开展仿真研究，殊不知这一函数产生的噪声是全频段噪声，而非与信号同带宽的带内噪声。与上述示例等价的一段MATLAB代码简要表示如下：

从上述MATLAB代码的最后一行可见：信号的相对幅度为1，添加的高斯白噪声的标准差相对值是10。于是很多研究者以此为依据，便断定：此时信号的SNR=-20 dB。虽然这一说法不能直接判为错误，但至少没有将信息表达清楚与完整。准确表述应该为：此时信号的全频段功率信噪比为-20 dB，且信号带宽与全频段带宽之比为1/1000。那么此时信号的带内信噪比又是多少呢？在用式（3）换算之前，为了更加清晰地展示这一问题，在MATLAB中将上述信号Mix_signal的功率谱绘制如图1所示。

图1 一个全频段功率信噪比-20 dB信号的功率谱

由图1可见，此时信号的带内功率信噪比为10 dB，这一图示与式（3）的理论关系完全一致。通过表1与图1的示例可知：一个带内功率信噪比为10 dB的信号，在选取不同的噪声带宽时，其全频段功率信噪比可以降低到-20 dB，甚至更低。在许多已经公开发表的文献中，在进行某种测量方法的性能评估时有一部分文献都采用了全频段功率信噪比，但此时又没有给出对应的信号带宽Bs与噪声带宽Bn的具体数值，表面上看是在负dB信噪比条件下能达到某一优良性能，但实际上按照信号的带内功率信噪比来评价，此时的SNR还是比较高的，这样一来就给读者和后来的研究者造成了误导。

2 能量信噪比与信号积累

2.1 信号的能量信噪比

实际上除了信号的功率信噪比之外，在数字通信系统中为了度量通信终端中数字解调器或译码器的性能，常常采用每传输1 bit的平均信号能量Eb（单位：J）与单位频带内的噪声功率n0之比，记为又称为比特能量信噪比[2，8]。如果把数字通信领域中的比特能量信噪比扩展开去，可将信号的能量信噪比定义为信号能量E与单位频带内的噪声功率之比，记为记功率信噪比度量中信号持续的时间为T（单位：s），显然有下式成立：

于是信号的全频段功率信噪比与能量信噪比之间的关系如下：

将式（3）代入式（5）可得信号的带内功率信噪比与能量信噪比之间的关系为：

式（6）中，Bs·T又称为信号的时带积。显然式（6）的物理意义体现为：在信号的带内功率信噪比保持一定时，信号的时带积越大，信号的能量信噪比也就越高。这实际上也是各种工程应用中采用信号积累来提升信噪比的本质驱动力所在。在许多工程应用性能评价中，例如数字通信解调译码的误比特率性能评价，匹配滤波的性能评价等，全部都采用信号的能量信噪比作为尺度，这同时说明：信号的能量信噪比相对于功率信噪比来讲，更能反映出其本质特征。所以在工程应用中全面的评价反映是同时给出信号的带内功率信噪比能量信噪比信号带宽Bs和信号持续时间T这4个参数中的任意3个，当然剩下的1个参数由式（6）也就自然确定了。另一方面，由式（6）可知：如果一个长时间持续存在的具有一定带内功率信噪比的信号，通过长期积累的方式则能够不断提升其能量信噪比。如此说来，从理论上讲，任意微弱的信号都可以通过积累方式而成为一个正dB数能量信噪比的信号，但在实际工程应用中却并非如此，关于这一点，接下来继续讨论。

2.2 信号积累与能量信噪比提升的工程上限

对于一个长时间存在的待测信号H，如果其信号的带内功率信噪比即这是一个负dB数的带内功率信噪比，只要长时间对这个信号进行持续测量，对应了信号持续时间可取无穷大，即T→∞，由式（6）可知：该信号的能量信噪比如此一来，测量精度就可做到无限高，从理论上讲，这一论断是完全正确的。虽然理想很丰满，但工程很残酷，在我们所处的这个物理世界中待测微波信号H几乎全部是一个时变信号，可将其看成是一个随时间变化的随机过程，记为H(t)，而且随测量精度要求的提升，H(t)还不是一个平稳的随机过程，而是一个时变均值的非平稳随机过程。如此一来，要对H(t)在时间上进行长时间累积后进行测量是办不到的，因为累积的前提条件是被测的信号参数是非随机的，在累积期间保持稳定。对于上述情况，在工程上只能假定在ΔT时段内被测的信号参数保持稳定，即该时段内的信号HΔT(t)保持近似平稳，在此假设条件下对信号进行累积，于是有：

式（7）中EΔ表示ΔT时段内的信号能量，显然也只能是一个有限数值了，不可能趋近于无穷大。

以测量一串重频为1 000 Hz、脉宽ΔTp=1 μs的单频脉冲串的载波频率参数为例说明如下。如果该脉冲串含有M个脉冲，单个脉冲的带内信噪比信号带宽Bs=2 MHz，于是由式（6）可得单个脉冲信号的能量信噪比从理论上讲，只要脉冲个数M→∞，就会有于是该脉冲串的载波频率测量误差εp就可达到无限小，即εp→0，对应的测量精度就可做到无限高。但实际上在M→∞的过程中，测试接收机自身都是不稳定的，其变频本振在随时间随机漂移；不仅如此，就连被对象本身（即脉冲串自身）的载波频率由于晶振的不稳定等工程因素也会随时间漂移，而且上述漂移是随机和非平稳的，记为fp(t)。我们对fp(t)进行测量，也仅仅是在可接受的工程误差范围内，在ΔTp时段内近似认为fp(t)保持稳定而已。

由此例可见，理论上的无限长时间积累在实际工程应用中是不可实现的，实际工程设备只能做到有限长时间的积累，而且这一有限的积累时间长度不仅受测量接收机性能的限制，而且还受被测对象的限制，并不是把测量接收机研制得无限接近完美就可以大幅度提升积累时间，从而实现测量精度的提升。因为在很多情况下，被测信号自身就是一个非平稳随机过程，对这类信号的测量，其测量时长是受测量精度限制的。要求的测量精度越高，对应的测量时间就越短，因为需要在这一短时间范围内将被测信号近似看成是一个平稳随机过程，如此一来，测量误差就不可能通过长时间积累而无限地减小。于是这就出现了一个矛盾，从某种意义上讲，这也反映了我们所处的物理世界中的“测不准现象”，即在某一应用条件给定时，其测量精度的工程上限也就随之确定了，从工程实现的角度讲，是无法突破这一上限的。但值得庆幸的是：在当前条件下，绝大部分工程应用所要求的精度远远没有达到这一上限值，所以目前的工程建设中还留有巨大的发展空间，值得大家继续研制高性能的测量仪器与设备去不断逼近这一个上限值。

3 信噪比对调制识别性能评估的影响

3.1 调制识别与信号的功率信噪比

信号的调制类型识别是一种很常见的工程应用，无论是通信侦察[9]、雷达侦察[10]，还是自适应通信传输[8]，其中都必然包含有调制识别这一重要环节。截止到目前为止，该技术方向上所发表的文献成百上千，如今新的研究论文仍在大量出版，全世界的科研人员如此之关注也反映出该问题在工程应用中的广泛性与重要性。在调制识别的研究结果中大家大多会提供不同方法之间的识别性能对比曲线，即在不同SNR条件下，各种方法之间的识别正确率曲线。当然，在一个给定SNR数值时，哪一种方法的识别正确率最高，这种方法的识别性能就会被评价为最好，这几乎成为调制识别技术方向上的一个公认的性能评价标准。

就这一个简单标准而言，当大家对SNR概念的理解出现差异时，不同技术文献所给出的研究结果也千差万别，造成了一定的混乱。在当前的大部分讨论调制识别的文献中，大多使用功率信噪比作为尺度。如前文所述，功率信噪比又细分为信号带内功率信噪比与信号全频段功率信噪比两种，由式（3）可知，即便信号的带内功率信噪比保持不变，不同的噪声带宽取值，会得到不同的全频段功率信噪比，从而造成这两种不同的功率信噪比之间差异巨大。如果大家仔细对比阅读一下调制识别方面的文献，就会发现有一部分文献均采用全频段功率信噪比来度量识别性能，但这些文献的作者又不给出所采用的噪声带宽的具体取值，于是就出现了在负dB数信噪比条件下，可达到80%～90%及以上的识别正确率，殊不知按照式（3）将信号的全频段功率信噪比换算成带内功率信噪比，这实际上是一个正dB数信噪比的信号，往往信号的带内功率信噪比有可能还非常高。以图1中的BPSK信号为例，如果对该信号做调制识别，在-20 dB的全频段功率信噪比条件下识别概率可达90%，其实该识别率是在10 dB的信号带内功率信噪比条件下达到的。如果我们在报道此实验结果时：含糊地宣称在-20 dB信噪比条件下可实现对BPSK调制的正确识别率达到90%，则会引发极大的关注，因为不知内情的读者可能误认为该方法性能实在是太优秀了，可事实并非如此，这仅仅是一场误会而已。也正是由于上述原因，文献作者根据这一仿真试验结果给出了极易产生误导的结论，这也是在调制识别技术方向上发表的大量文献所给出混乱结果的重要原因所在。

而消除上述乱象的一种方法就是：在SNR定义上采用信号的带内功率信噪比，这样就消除了全频段功率信噪比评价中噪声带宽随意取值的弊端；或者在采用信号的全频段功率信噪比时，一定要给出信号带宽与噪声带宽的比值，这样才能做到性能评价尺度的统一。但即便做到这一点，仍然还存在一定的问题，下面接着探讨。

3.2 基于信号带内功率信噪比的综合调制识别方法

在将调制识别技术方向上的SNR全都统一为信号的带内功率信噪比之后，就可以将绝大部分识别方法在不同SNR条件下的识别概率在同一张图上绘制出来。以图2所示为例，图2中绘制了3种方法在不同信号带内信噪比条件下的识别性能曲线。这样一来，各种方法的性能优劣也就一目了然了。在给定的信号带内功率信噪比取值下，哪一种方法具有最高识别概率，则这种方法就是在这一信号带内功率信噪比条件下的当前最优方法。

图2 在不同信号带内功率信噪比条件下3种方法的识别概率性能曲线

如此一来，通过博采众长的方式，可设计一种更好的调制识别方法。首先对待识别的信号进行带内功率信噪比的估计，然后根据估计值查找已有方法的识别性能曲线，选取在该带内功率信噪比条件下识别概率最高的方法来对目标信号进行调制类型识别，则可得到最高的识别概率，这就是基于信号带内功率信噪比的综合调制识别方法。如果估计出的带内功率信噪比不同，当前的识别方法也会随之进行调整，但始终保持最佳。以图2中的3种方法为例，首先估计待识别信号的带内功率信噪比，如果在[5,9.5]dB范围内，则采用方法2；如果在(9.5,14.5]dB范围内，则采用方法1；如果在(14.5,20]dB范围内，则采用方法3。如此一来，新方法的识别性能曲线如图3所示，显然综合出的新方法的识别性能优于图2中的任何一种方法。

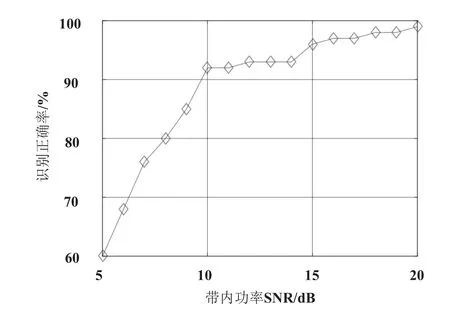
图3 新方法的识别概率性能曲线

由此可见，如果将截止到目前所有公开文献发表过的方法在统一的应用条件与统一的评价尺度下综合在一起，将产生一种具有最高识别率的特殊方法，这也是调制识别技术方向上新的思路。

3.3 对长时间持续信号进行多次识别

似乎在前一节分析完之后，SNR与调制识别之间的关系也就十分明确了，但事实并非如此。即便大家统一使用信号的带内功率信噪比作为衡量尺度，对各种调制识别方法性能的精确对比仍然不能完成，因为还有一个尺度没有统一，这就是信号的持续时间。关于这一点，与前面的式（6）有这类似的性质，即通过增加测量时间来获得积累所带来的好处。

对一个长时间持续的信号反复进行调制识别，如果每一次识别结果的正确率记为pR，错误概率记为pW，显然pR+pW=1。只要pR＞0.5＞pW，我们就可以通过多次识别之后，对识别结果进行统计，取其中次数占优的结果作为最终识别结果，这样即可不断地提升识别的正确率。这一做法可以通过如下的定理来得以部分解释。

定理1：在正确识别率pR＞0.5时，一共进行了2n-1次调制识别，且n≥1，如果有一种识别结果出现了至少n，则将此结果作为最终识别结果输出。按照这样的多次识别后的统计占优的判决方法，最终识别结果的正确率将会随着n的增加而不断增加。

在证明这一定理之前，我们先举例说明该定理的应用示例。例如对一个调制类型为A的信号进行调制识别，正确识别出该信号的调试类型“是A”的概率为60%，而识别成“不是A”的概率为40%。如果对该信号只进行1次识别，则识别正确率为60%；如果对该信号进行3次识别，其中有2次或2次以上识别为A，则将最终识别结果确定为A，这样做，识别正确率为64.8%，相对于只进行1次识别提升了4.8%；如果对该信号进行5次识别，其中有3次或3次以上识别为A，则将最终识别结果确定为A，这样做，识别正确率为68.26%，相对于只进行3次识别提升了3.46%。下面用数学归纳法来证明上述定理。

如上所述，在m=2,3时定理是成立的；假设该定理在n=m，m≥3条件下是成立的，此时一种识别结果至少出现m次的概率pm如下式所表达：

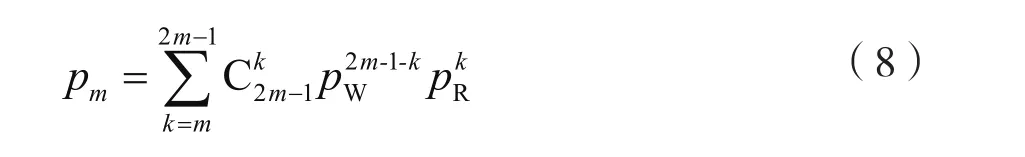
且pm相对于在n=m-1条件时的识别概率要大，即便pm＞pm-1。当n=m+1时，此时识别结果中至少出现m+1次的概率pm+1可由下式计算：

由此可见：定理得证。

按照该定理就会引出一个问题，只要单次识别正确率高于50%，如果对同一信号进行多次识别，识别正确率就可以不断得以提高，如此一来，如果不统一规定识别次数，则各种调制识别方法的性能对比又将失去公平。但如何才能合理地统一确定好识别次数这一参数呢？这还需要借助于信号的能量信噪比的概念。

3.4 调制识别与信号的能量信噪比

由前述讨论可知：为了对调制识别的性能做出公平合理的评估，除了给定信号的带内功率信噪比之外，还需要明确信号持续时间T和信号带宽Bs，这样才能完全确定调制识别的应用边界条件，在此情况下再来对比各种不同识别方法的识别正确率，则可以在一种比较公平的环境下用统一的尺度做出评判。实际上由式（6）可知，在上述3个参数都确定的条件下，也就确定了信号的能量信噪比这就意味着在信号的调制类型识别中，所利用的目标信号的能量多少也会对识别结果产生重要影响。

关于这一点，在雷达脉冲信号的调制识别与通信连续波信号的调制识别的工程应用差异中早就有所体现，只不过大家并没有特别关注而已。对于雷达脉冲信号的调制识别来讲，需要对截获到的每一个脉冲信号的调制类型做出识别，从而为后续的脉冲分选提供信息输入。显然，雷达脉冲信号的调制识别持续时间仅仅只有一个脉冲宽度的时间，这与常见的一直存在的通信连续波信号的调制识别有着很大的区别。如果从数理统计的角度来看待这一差异，雷达脉冲信号的调制识别实际上是在有限持续时间下的识别，属于小样本的统计处理；而一直存在的通信信号的调制识别，则属于大样本的统计处理。大家都知道：小样本处理比大样本处理的难度要大得多，所以很多适用于通信信号的调制识别方法很难直接应用于雷达脉冲信号的调制识别之中。如果真正要将二者应用中的各种方法的识别性能进行对比，则需要引入信号能量信噪比的尺度，即在明确信号的带内功率信噪比之外，还需要统一规定好信号的持续时间长度和信号的带宽，从本质上讲，也就自然确定了统一的信号能量信噪比。在此条件下进行不同调制识别方法的性能综合评判，这才更公平、更合理，更能体现不同方法在不同应用条件下的优势与不足，从而为实际工程应用提供指导。

4 结 语

针对当前工程应用中不同信噪比定义给工程测量所带来的乱象，本文对信噪比概念进行了重新的梳理与细致的解释，通过信号带内功率信噪比与全频段功率信噪比之间的差异与关系的分析，解释了测量与识别等应用中不同评价尺度所引发混淆的原因；通过信号功率信噪比与能量信噪比之间的关系的梳理，揭示了信号累积对测量精度的影响程度，同时也解释了工程应用中不可能通过无限长的信号积累来获得高测量精度的现实原因。在此基础上，以调制识别为例，分析了调制识别的性能与信号的带内功率信噪比、信号的能量信噪比之间的关系，指出了通过全面统一评价尺度来实现公平合理的调制识别性能评价的方法与途径。以上探讨有助于大家进一步加深对信噪比概念的理解，也有助于在工程测量等应用中更好地使用信噪比这一概念与尺度。