基于最小二乘法的BLDCM霍尔安装偏差补偿方法
2019-09-04黄立立徐奇伟李蓬威
黄立立,徐奇伟,李蓬威,杨 云
(重庆大学,重庆 400044)
0 引 言
无刷直流电动机(以下简称BLDCM)以其功率密度高、动态性能好和可靠性高等诸多优点,在工业驱动和小功率位置伺服系统等领域得到了广泛的应用。BLDCM正弦波电压控制输出转矩平稳,且系统的振动和噪声小。正弦波控制BLDCM需要得到精准的转子位置信号,从而输出正弦电压驱动电机运行,如何利用低精度霍尔传感器获得高精度且平稳的位置信号,是实现BLDCM正弦波电压高性能控制的关键[1-3]。
文献[4]提出了采用两相正交型霍尔传感器检测转子位置;文献[5]提出了构造矢量跟踪观测器的方法,不仅能够补偿位置误差,而且提高了系统的动态性能;文献[6]基于矢量跟踪观测器提出了磁链观测器,可以补偿任何时刻转子位置偏差,但是观测器法对电机参数的依赖性强,且观测器构造复杂;文献[7]采用基于最小二乘法的插值法估计转子位置,保证了信号的连续性与准确性,但是噪声含量高,且滞后性明显。
本文针对BLDCM三相霍尔位置传感器安装角度偏差,提出了一种基于最小二乘法的补偿算法。首先阐述了基于霍尔传感器的BLDCM驱动系统,然后针对霍尔传感器安装偏差,说明了直接矫正方法的缺陷与不足,提出了假设某相霍尔传感器无误差的补偿方法,再叠加该相的补偿量,使得补偿后的转子电角度能够较准确地表示实际转子电角度,最后,通过仿真和实验,验证了该方法的有效性。
1 BLDCM转子位置估计方法
1.1 霍尔传感器安装位置偏差
图1为BLDCM霍尔传感器位置安装误差原理图。Ha,Hb和Hc为检测A,B,C相反电动势的霍尔传感器,霍尔传感器滞后相应的绕组轴线90°电角度,3个霍尔传感器的安装在空间上互差120°电角度。转子旋转时,相绕组反电动势过零的时刻就是该相霍尔信号跳变的时刻。当转子旋转一个周期,一个霍尔传感器完成一个周期的检测,输出50%占空比的方波信号,3路霍尔信号互差120°电角度,一个周期可以检测到6个转子位置,即将一个周期划分为6个扇区。
图1中,当位置安装存在偏差时,霍尔传感器检测到的转子位置与理想的转子位置之间存在偏差。当霍尔传感器安装位置超前时,提前检测到磁场过零,相邻的两个扇区所对应的电角度前一个变窄,后一个变宽,安装位置滞后时的情况与之相反,但检测到的转子位置被认为是理想的转子位置。虽然每一个扇区所对应的电角度不再是60°,但却被认为是理想的转子位置,这对于BLDCM控制有严重的影响,会引起电流畸变和转矩脉动,严重时烧毁电机,造成不可逆转的损毁。
1.2 平均速度补偿
很多文献研究了基于上一个扇区的平均速度,预测下一个扇区的位置估计方法[8]。其基本原理:
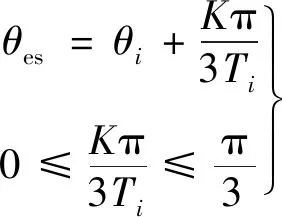
(1)
式中:θes为估计的转子位置;θi为霍尔传感器检测到的转子位置。霍尔传感器位置存在较大位置偏差时,式(1)的补偿效果变差。由于相邻两个扇区之间的电角度间隔不再是60°,即使电机匀速运行,估算的平均速度和转子位置偏差仍较大。相对来说,通过更多的扇区估算转子速度可以减小位置估计偏差。假设电机匀速运行,对比不同的平均速度补偿方法。
同一个霍尔传感器,在检测出一个完整的机械旋转时,估算的转子角速度:
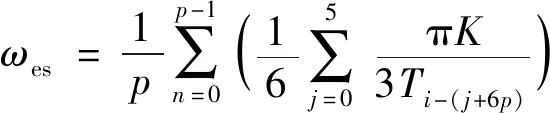
(2)
式中:K为最近一次霍尔信号跳变的计数值;p为电机的极对数;Ti-(j+6p)是扇区i前面的第j+6p个扇区的时间。虽然这种方式估算的是真实机械速度,但通过一个机械周期计算机械角速度,极大地降低了快速性,不能达到电机的动态响应指标。
多数情况下,可以认为BLDCM转子磁体的安装是完全对称的(实际工程中是可以这样认为的),这样就不会存在每个电周期计算的平均速度不相等问题,只需要计算一个电周期即可:

(3)
进一步简化式(3),可以用前3个扇区计算平均速度:

(4)
以A相反电动势为例,假设转子逆时针旋转,转子N磁极和A相绕组轴线对齐时,检测到一个边沿信号(Ha的磁场极性一次跳变N—S),当转子S磁极和A相绕组轴线对齐时,又检测到一个边沿信号(Ha的磁场极性一次跳变S—N),在一个霍尔传感器的两次跳变间,可以准确知道转子转过180°电角度。
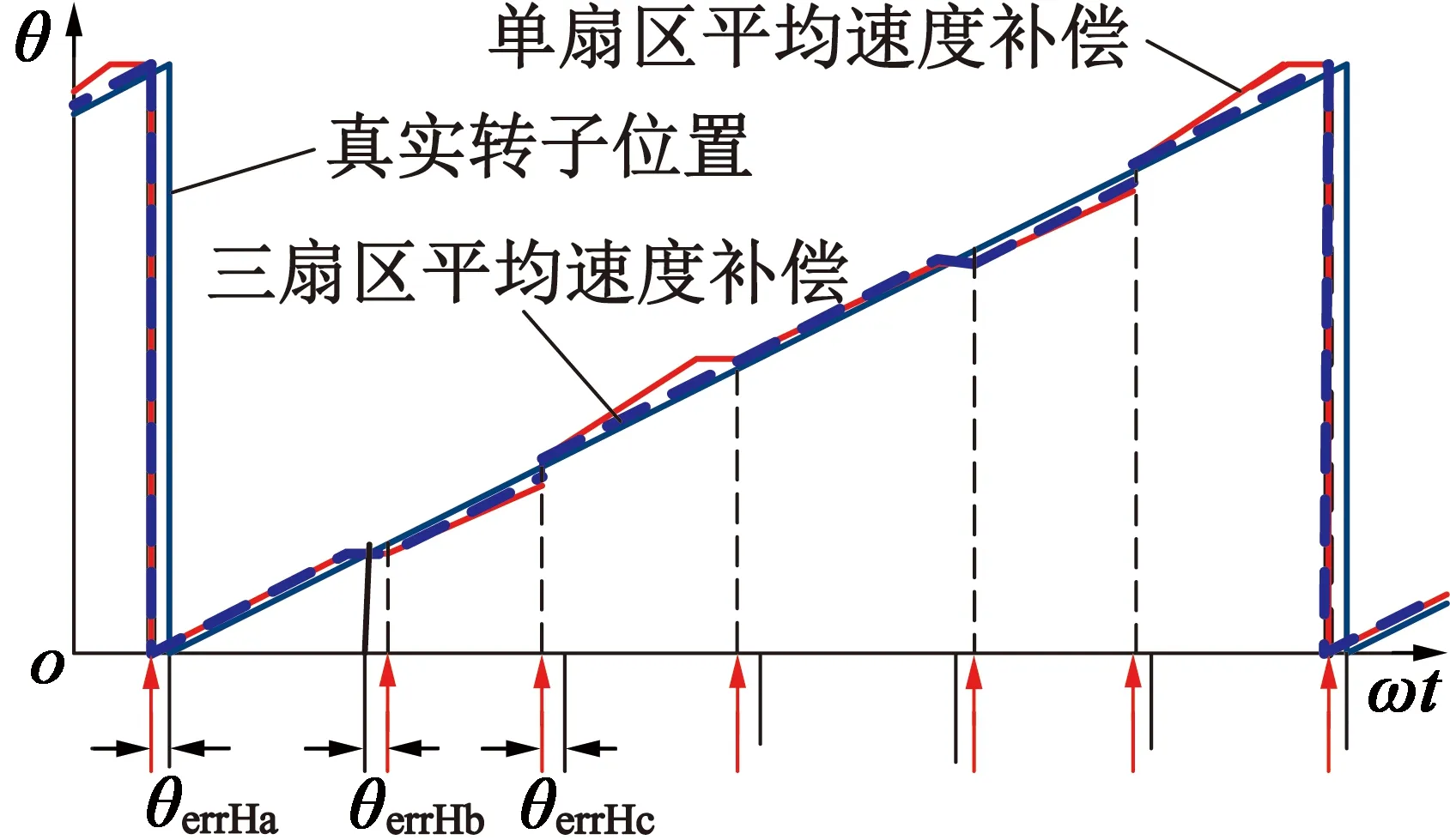
图2 两种平均速度位置补偿结果
基于前3个扇区计算平均速度的方式,在一定程度上保证了速度响应的快速性;同时在一定程度上减小了位置安装存在偏差时的位置估计偏差。其估算方式:
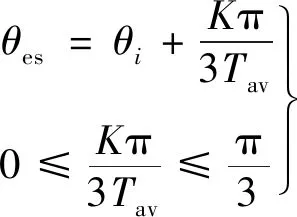
(5)
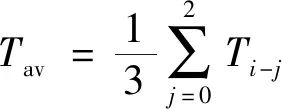
如图3所示,采用3个扇区的平均速度去估算转子位置与采用前一个扇区的估算结果相比,转子位置估偏差减小。但由于在每一个霍尔边沿信号触发的时刻,每一个霍尔传感器存在绝对位置偏差,所以估计的位置信号依然存在跳变,而这种跳变对于高性能的BLDCM控制系统极为不利。因此需要减小或者消除霍尔传感器的安装偏差,提高电机性能。
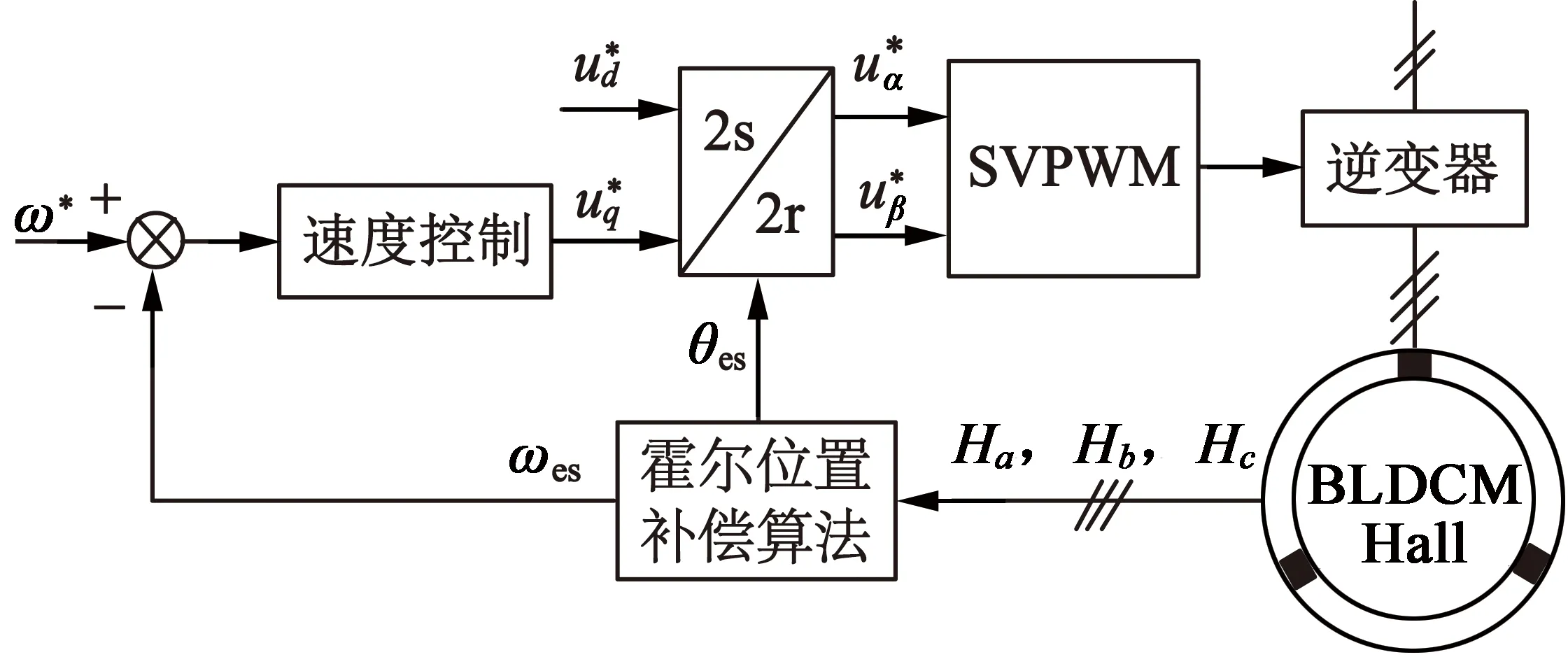
图3 采用正弦波电压的BLDCM控制方案
2 安装偏差最小二乘法补偿
2.1 绝对位置偏差与相对位置偏差
由以上分析可知,霍尔传感器安装偏差导致对应扇区电角度不是60°,但控制器(一般为单片机)依然以霍尔无偏差时的信号为准,即认为Ha上升沿时,A相反电动势过零,B,C相亦然。
为了分析方便,此处约定霍尔传感器顺时针偏差为正偏差,逆时针偏差为负偏差(该偏差为绝对位置偏差)。假设Ha,Hb和Hc的绝对位置偏差为θerrHa,θerrHb和θerrHc,在电机匀速运行时,控制器可以检测到每个扇区的对应电角度:
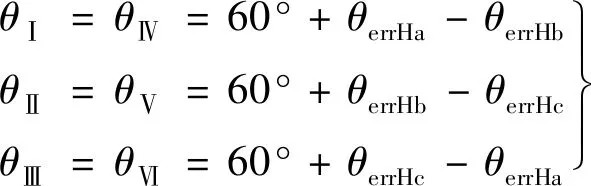
(6)
将式(6)写成矩阵形式:
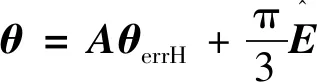
(7)
通过式(5)的估计方法,控制器能够计算出θerrH,该项值为两个相邻霍尔传感器位置偏差之和,即绝对位置偏差,体现的实际意义是每一个扇区相对于60°电角度的增量。如果某扇区开始的霍尔信号提前发生跳转,扇区变宽;反之同理。如果某扇区结束的霍尔信号提前发生,扇区变窄;反之同理。即扇区开始和结束的霍尔信号对扇区宽度的变化趋势起相反作用。因此,定义每个扇区的相对位置偏差,即该扇区结束信号对应霍尔相对于该扇区开始信号对应霍尔安装角度减去60°的值。
控制器计算出该项的方法是,在某一个电角度周期中,令检测到的每个扇区的时间为TⅠ~TⅥ,则每个扇区的电角度:
(8)
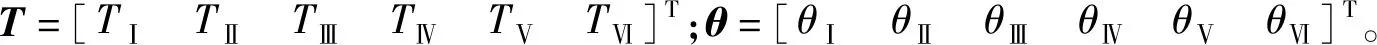
将式(8)代入式(7)中,得:
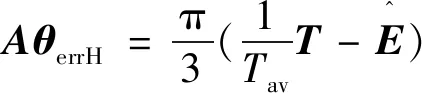
(9)
由于控制器无法检测绝对位置偏差,所以只能从式(9)中估计出一个绝对参考位置,用于修正Ha,Hb和Hc的绝对偏差。
2.2 最小二乘法补偿方案
前面分析了霍尔传感器存在绝对位置偏差时,每个扇区的变化情况,同时得到了在实际系统中只能检测到式(9)的值,因此,需要通过式(9)找到一个补偿量,使得检测到的转子位置能够较准确地表示转子的实际位置。
式(9)的右边可以通过控制器的定时器计算。由式(6)可知,可以选取连续的3个扇区,就足以反映绝对误差的全部信息。选取扇区Ι,Ⅱ,Ⅲ,将式(9)缩减成下式:
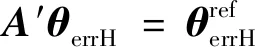
(10)
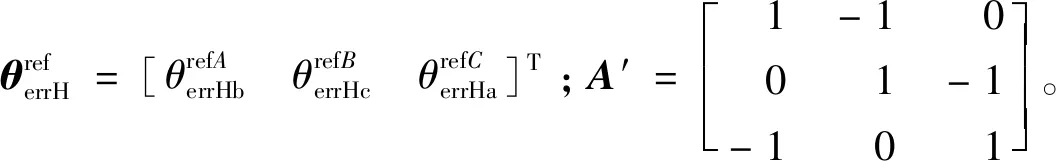
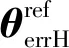
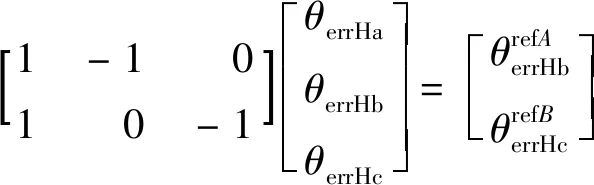
(11)
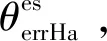
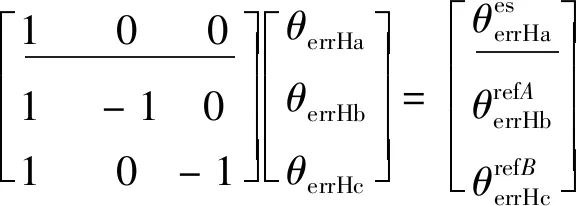
(12)

(13)
我们期望基于估计Ha的绝对偏差表示3个霍尔传感器的绝对偏差的方差最小,在实际工程中期望霍尔传感器安装是准确无误的。因此,可以建立估计的绝对位置偏差的最小方差估计:
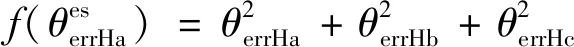
(14)
将式(13)代入式(14),并求其导数,得到最小值点:
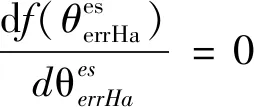
(15)
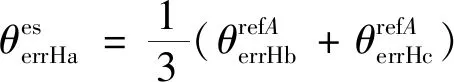
(16)
虽然式(16)表示的是估计出的Ha绝对位置偏差,但Hb,Hc的估计绝对位置偏差同样可以表达出来。完整的绝对位置偏差修正方程:
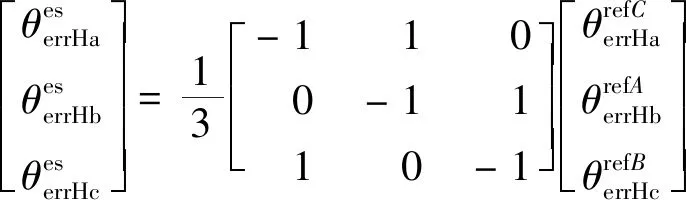
(17)
式(17)右边是霍尔的相对位置偏差,可以通过控制器的定时器测出对应的时间计算得到,式(17)左边是对每个霍尔的绝对位置偏差修正值,这样可以修正式(5)霍尔位置补偿方案:
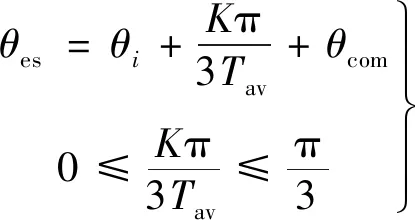
(18)
式中:θcom是在原来的补偿方案中对霍尔位置绝对偏差的估计修正项。在控制过程中,该项通过前3个扇区的时间实时计算,迭代公式:

(19)
化简后:
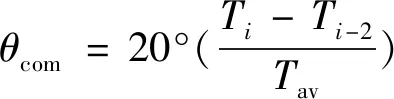
(20)
3 仿真和验证
为了对比分析本文的补偿方法的有效性,采用图4的BLDCM速度正弦波电压控制方式,对比分析电机运行时的定子电流波形。
电机采用5对极12槽带霍尔传感器的BLDCM,通过空载反电动势标定,确定出Ha,Hb,Hc的位置偏差为1.8°,0.9°和-2.4°。同时,Rs=0.113 Ω,Ld=88 μH,Lq=138 μH,ψf=0.022 Wb。设定仿真模型参数和实际电机参数一致,控制器控制周期为100 μs,采用带2 μs死区、频率10 kHz的PWM,得到仿真结果如图4所示。

(a) 传统方法三相电流
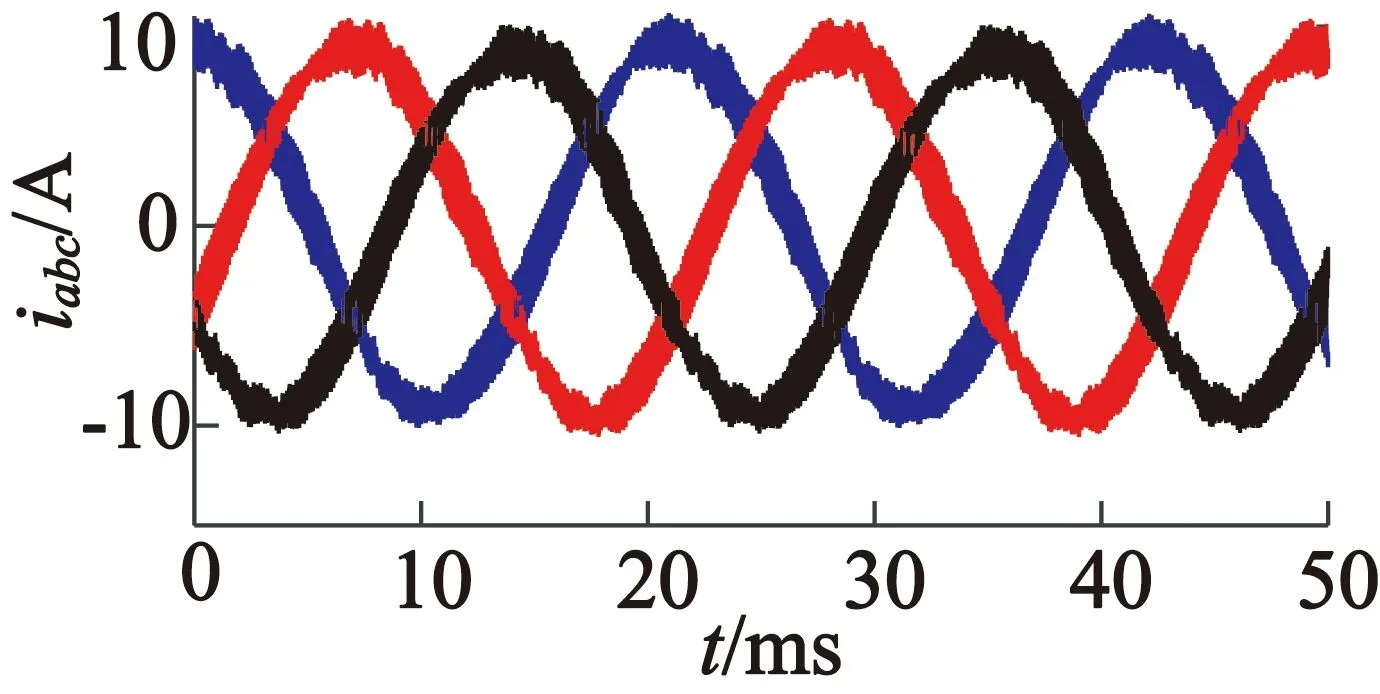
(b) 本文方法三相电流

(c) 传统方法位置偏差
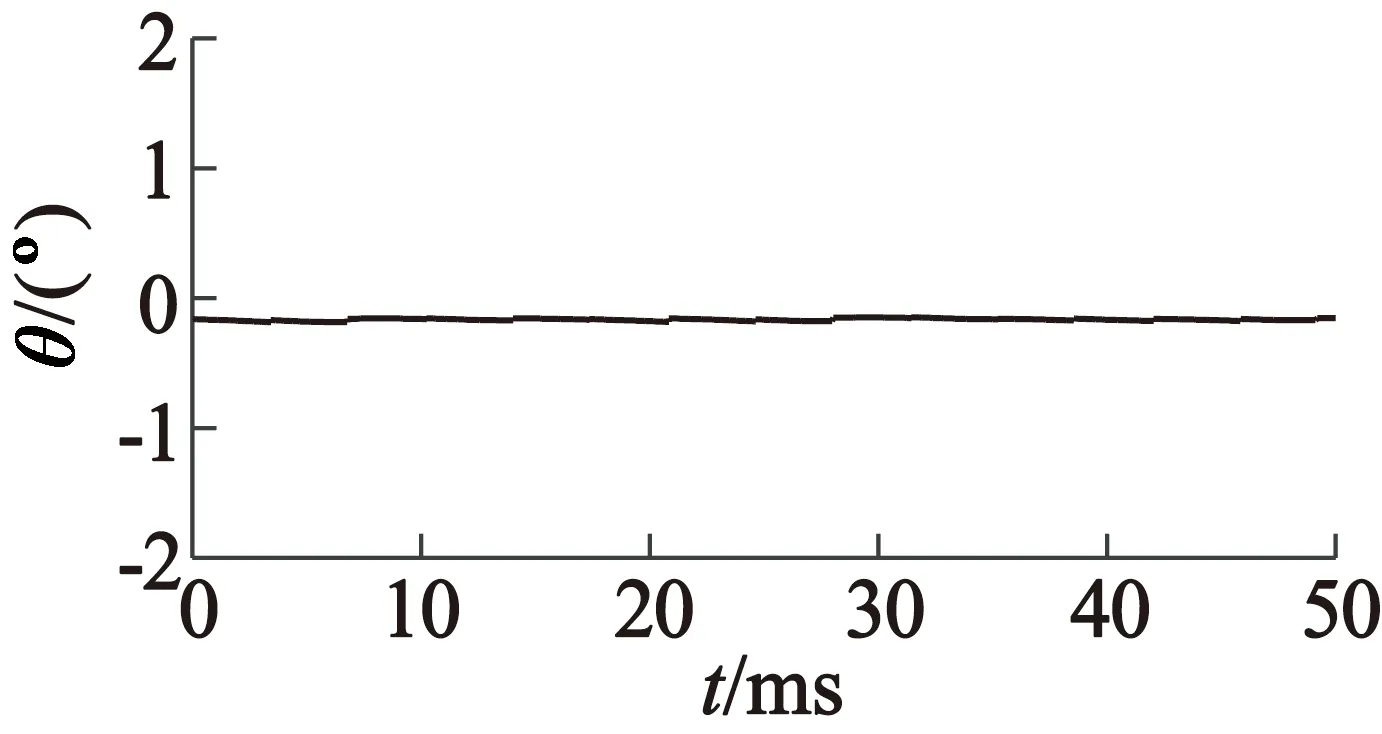
(d) 本文方法位置偏差
图4仿真对比
当采用单扇区平均速度估计转子位置时,估计位置偏差达到7°;同时由于位置的偏差,导致输出三相电压严重畸变,且三相电流的不对称性,控制效果差。采用本文的霍尔偏差修正方法后,位置偏差为0.1°,并且只存在初始偏差,没有位置波动,三相电流正弦度好。
实验采用一套基于STM32F103C8T6处理器的BLDCM实验平台,对一台车用功率800 W的BLDCM实验,该电机采用三相霍尔传感器检测位置信号。如图5所示,通过实验对比,采用本文补偿方法后电流的谐波含量明显减小,正弦度更好。实验结果和仿真结果一致性良好,验证了本文提出方法的有效性。

(a) 实验平台
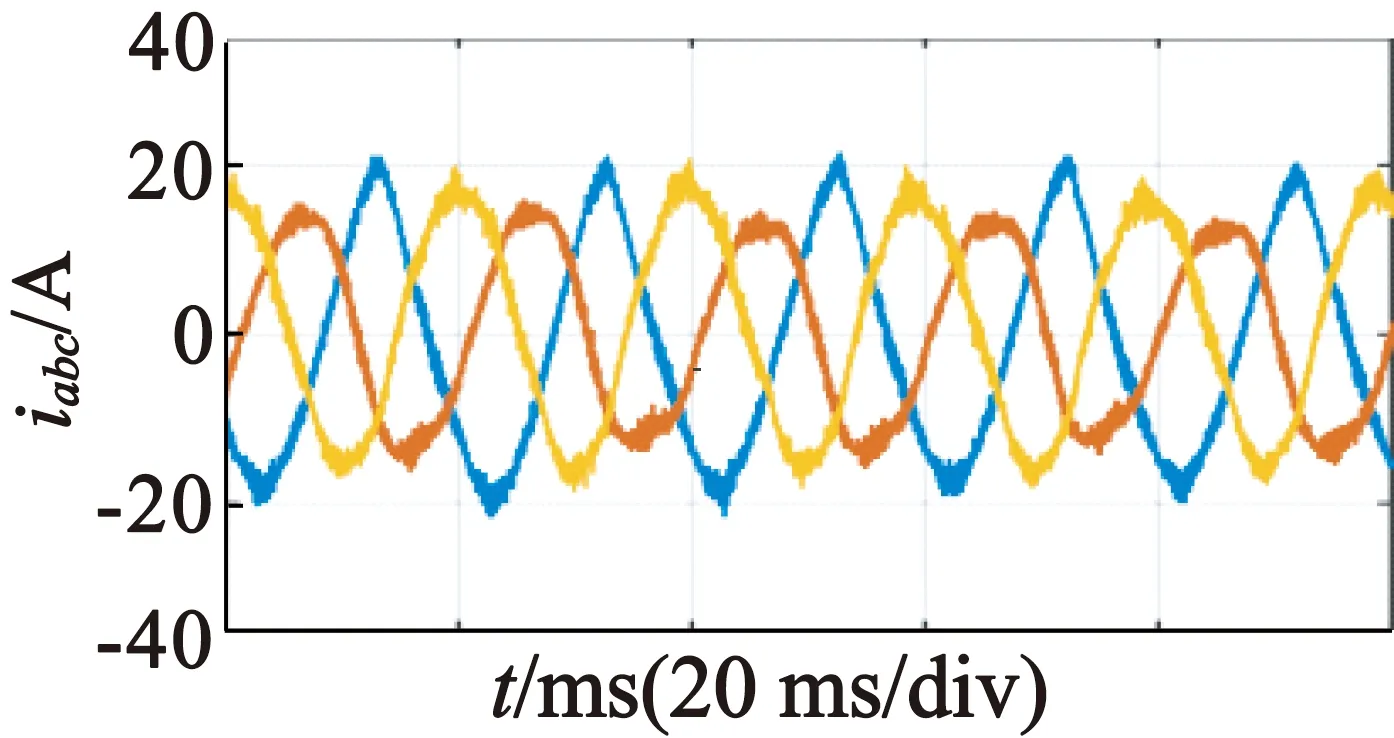
(b) 传统方法三相电流
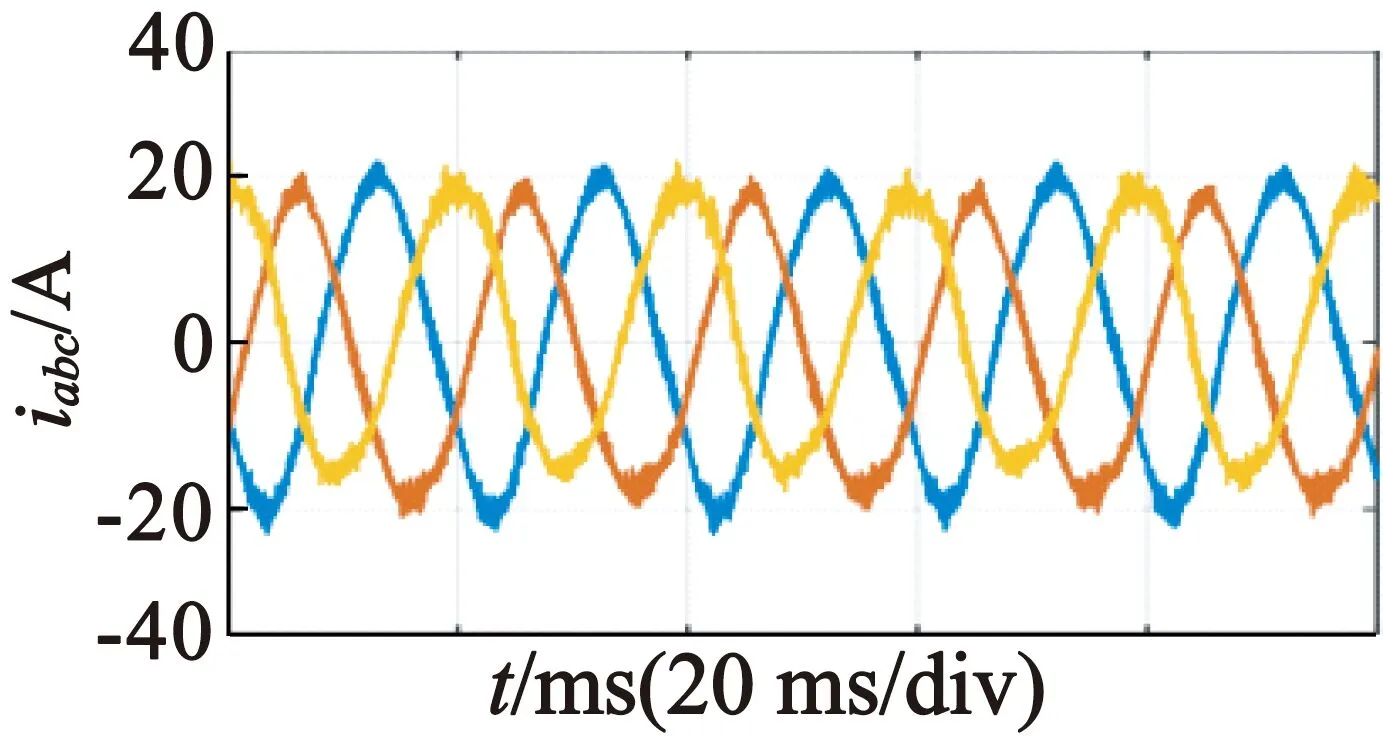
(c) 本文方法三相电流
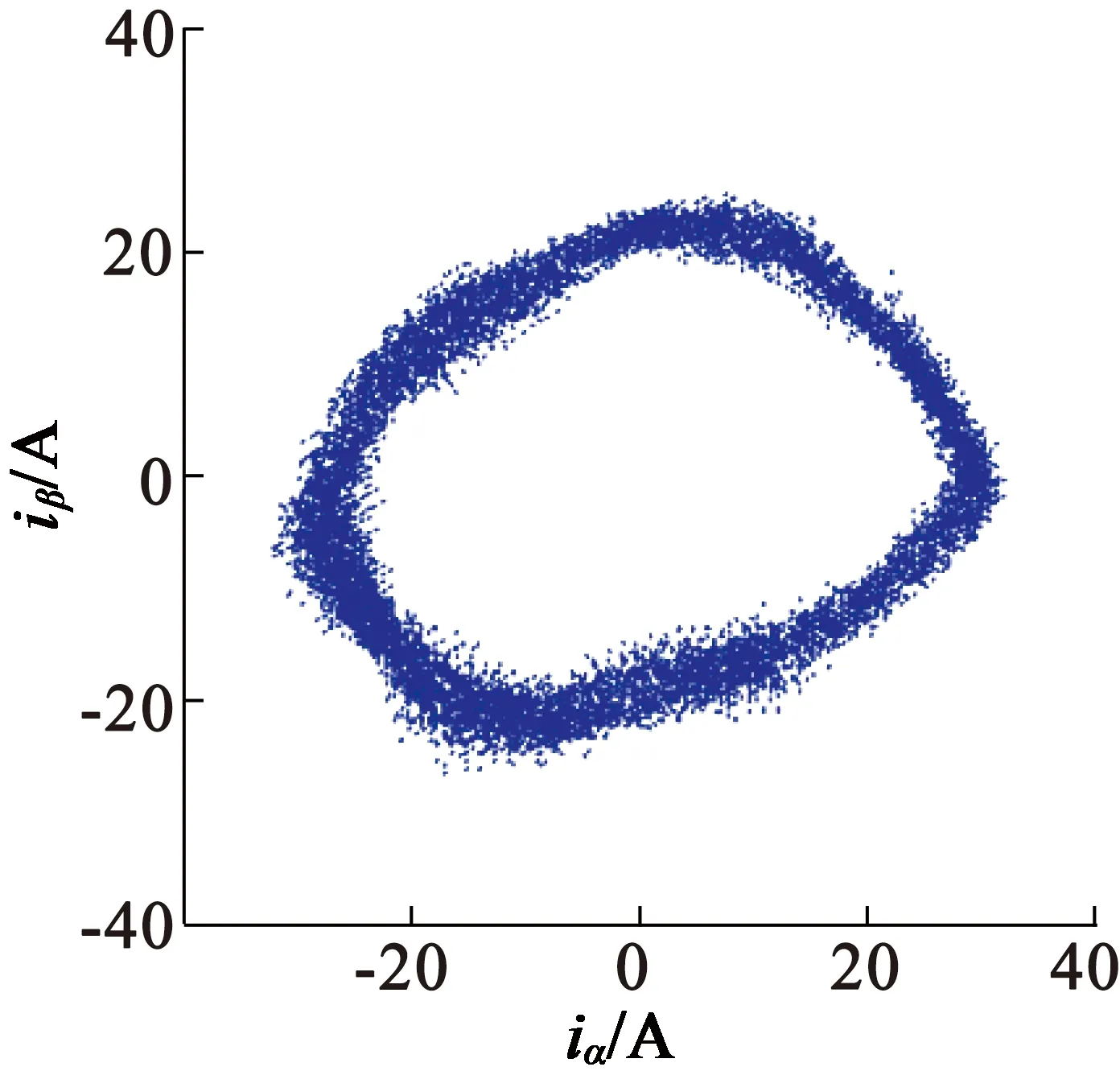
(d) 传统方法电流矢量轨迹
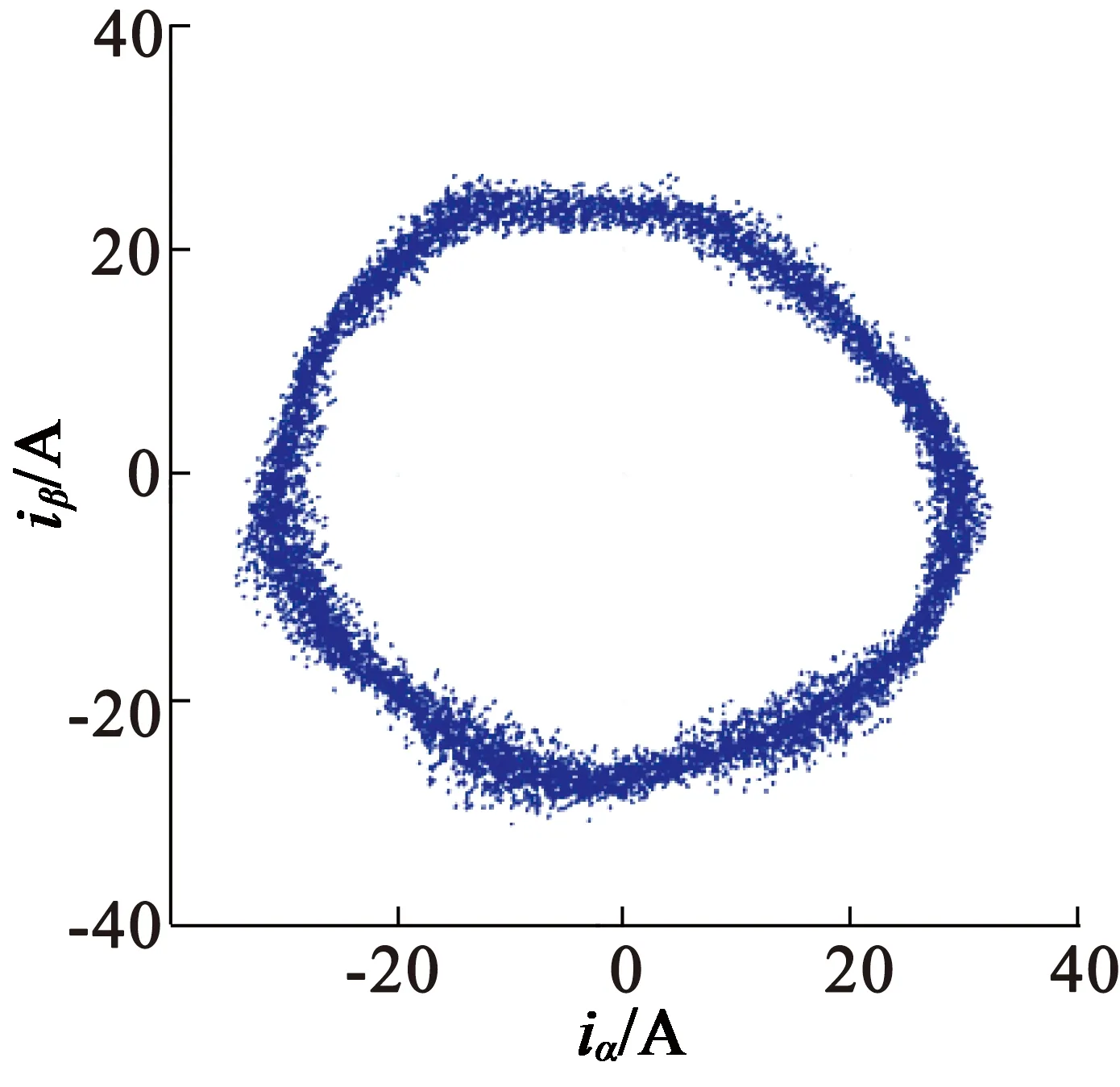
(e) 本文方法电流矢量轨迹
图5实验平台和实验结果
4 结 语
本文阐述了BLDCM霍尔位置传感器的检测原理,分析了在霍尔位置存在安装偏差时的传统位置补偿方法的不足,基于最小二乘法理论,提出了一种霍尔绝对位置偏差的补偿方法,并给出了该方法的在线迭代算法。在仿真和实验中对比了本文方法和传统方法的转子位置偏差和电流波形正弦度,结果表明,本文提出的方法减小了转子位置偏差,可以较准确地得到电机转子的实际位置,同时提高了BLDCM的电流正弦度。
