基于电流残差矢量的逆变器开路故障诊断

孙晟桐，刘 剑，宋吉江，徐 飞，谭芳堃

(山东理工大学，淄博 255000)

0 引 言

永磁同步电机(以下简称PMSM)由于具有高功率密度、高效率、高可控性等优点，正在被越来越多地利用在电动汽车、航天航空仪器和军事等众多领域中。PMSM驱动系统发生的开路故障会对PMSM的可靠性产生影响。为了不影响PMSM在故障条件下的运行，需要采取有效的容错控制[1-3]。

近年来，国内外已提出了多种方法用于诊断逆变器中的开路故障。根据需要使用的变量，逆变器故障诊断方法可大体分为两类，即基于电流和电压的故障诊断方法。尽管基于电压的故障诊断方法具有检测周期短、可靠性强等众多优点，但该方法通常需要电压传感器，电压传感器会增加系统的复杂性和成本。因此，与基于电压的诊断方法相比，基于电流的诊断方法更为简便。

基于Concordia电流模式的半径，文献[4]提出电网中性点钳位逆变器开关发生开路故障的故障检测方法。该方法不仅可以检测故障状况,还可识别出故障位置。基于应用开关函数的双傅里叶变换技术，文献[5]提出通过分析逆变器在正常和发生开路故障时直流侧电流低频部分的频率成分的变化，对逆变器的开路故障进行诊断。文献[6]提出通过测量定子电流来诊断逆变器中开关的开路故障，该方法以利用傅里叶级数对定子电流的故障后轨迹进行解析推导为基础，通过在24个等距扇区中划分平面来计算轨迹的直方图，以此作为故障诊断依据。与文献[4]相比，文献[6]可对多个开关开路故障同时进行诊断。文献[7]提出将测量的相电流与从主控制系统获得的对应参考信号作差求平均值，然后将此平均值与测得的相电流平均值为依据，获得诊断变量，最后定义阈值，通过对诊断变量和阈值的比较来诊断故障。基于两相输出电流轨迹，文献[8]提出通过观测和辨识在笛卡尔坐标系下由两相电流合成的椭圆倾角和离心率，以此诊断开路故障。基于Blanke M提出的累积和算法[9]，文献[10]提出将测得的三相定子电流幅值和瞬时频率分别生成两组故障指数，对开路故障进行高柔性的诊断。基于电流矢量特征分析，文献[11]提出以电流矢量的瞬时频率特征和瞬时角度特征为依据对故障进行快速诊断与定位。此外还有其他相对成熟的故障诊断方法被提出[12-14]。文献[12]采用模糊专家系统，提出基于测量输出电流波形的离散小波变换分析的诊断方法。文献[13]提出分别通过小波变换和傅里叶变换对电动机转速信号进行时间-频域率对比分析的方法。文献[14]提出通过逻辑分析对称分量中的基本信号的幅度和相位角变化的模式来提供故障类型。以上的故障诊断方法多是基于电流信息的故障诊断策略，诊断时间往往在一个基波周期以上；同时，由于在闭环系统中电流传感器的修正作用，诊断策略的可靠性较低。因此，需要一种既可以缩短诊断时间，又可以避免使用额外传感器的故障诊断策略。

本文研究了基于电流残差矢量的开路故障诊断方法。分别构建了基于PMSM驱动系统逆变器的混合逻辑动态模型和二阶滑模电流观测器，在发生开路故障后，将混合逻辑动态模型输出的电流与二阶滑模电流观测器输出的实际电流作差，得到电流残差矢量，以此为依据对开路故障进行诊断和定位。当电流残差矢量的幅值大于设定的阈值，则表示发生开路故障。此外，将电流矢量平面划分为六个平面，根据相位角定位故障开关。最后，基于MATLAB/Simulink对所提出的诊断方法进行了仿真分析，验证了该方法的有效性。

1 PMSM驱动系统混合逻辑动态模型

1.1 PMSM的电流数学模型

图1是PMSM驱动系统示意图。由图1可知，PMSM的数学模型如下:

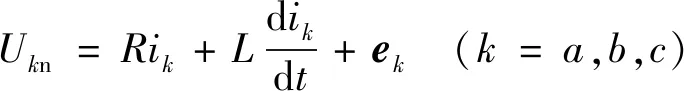
(1)

式中:Ukn为三相定子电压；ik为三相电流；L和R分别为定子电感和定子电阻；ek为反电动势向量，且:

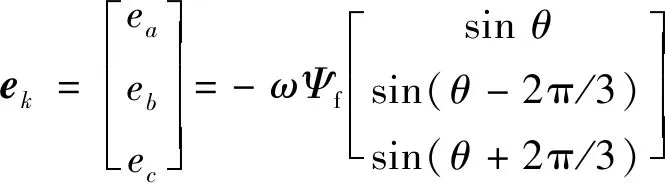
(2)

式中:θ为d轴逆时针旋转到α轴的电角度。

根据基尔霍夫电压定律，可得下式:

Ukn=Ukg-Ung

(3)

这里电机是星形方式连接，所以:

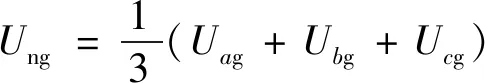
(4)

联立式(1)、式(3)和式(4)，得到PMSM三相电流的数学模型表达式：

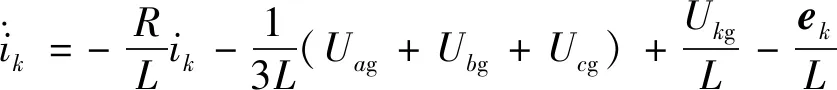
(5)

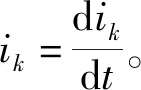
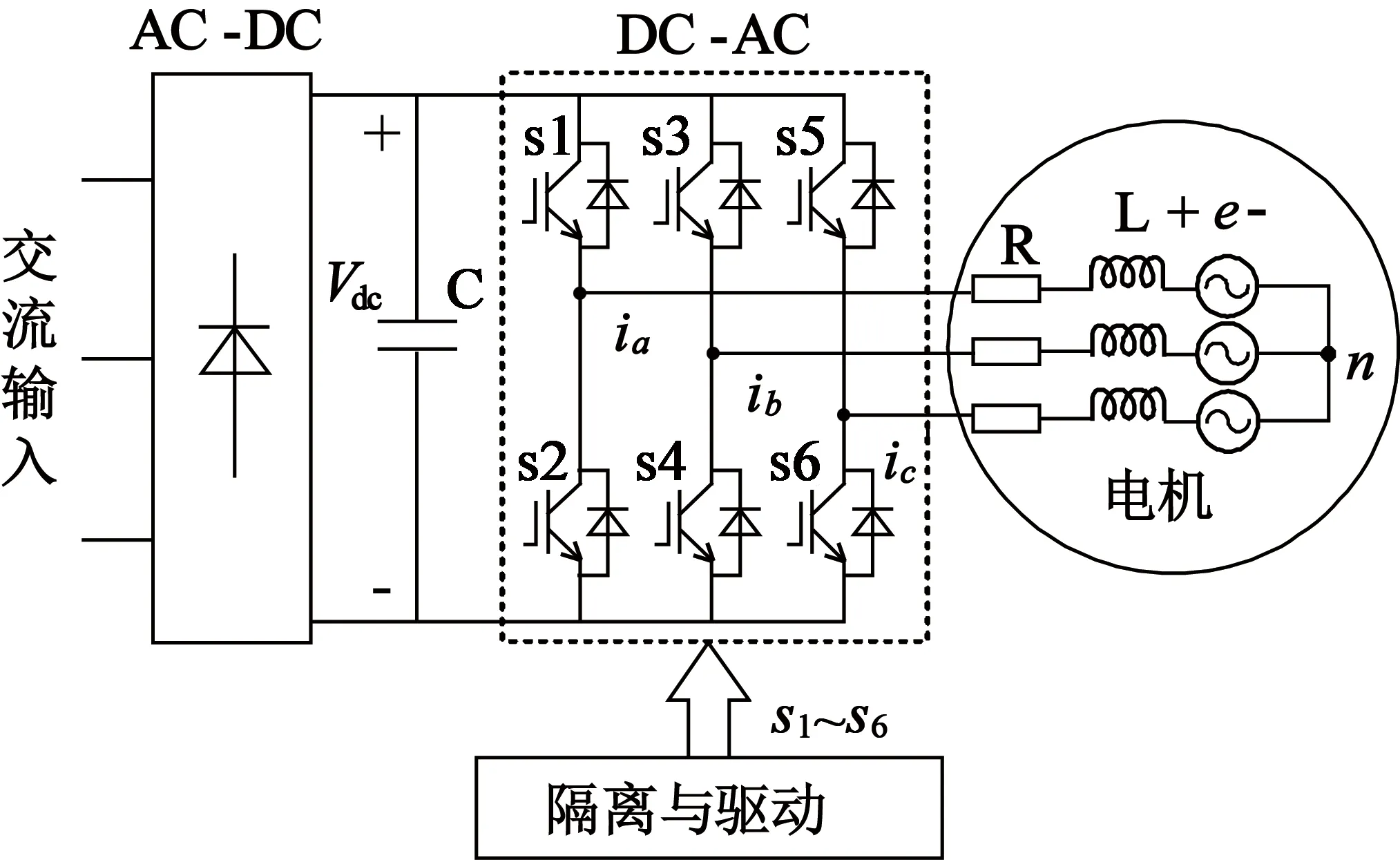
图1PMSM驱动系统示意图

1.2 PMSM驱动系统混合逻辑动态模型

如图2所示，用6个离散控制变量s1～s6表示逆变器开关的关断情况。当sj导通时，sj=1;当sj关断时，sj=0。再定义用来反映电流方向的离散条件变量δk，规定流向绕组为正方向。ik为正时，δk=1；ik为负时，δk=0。

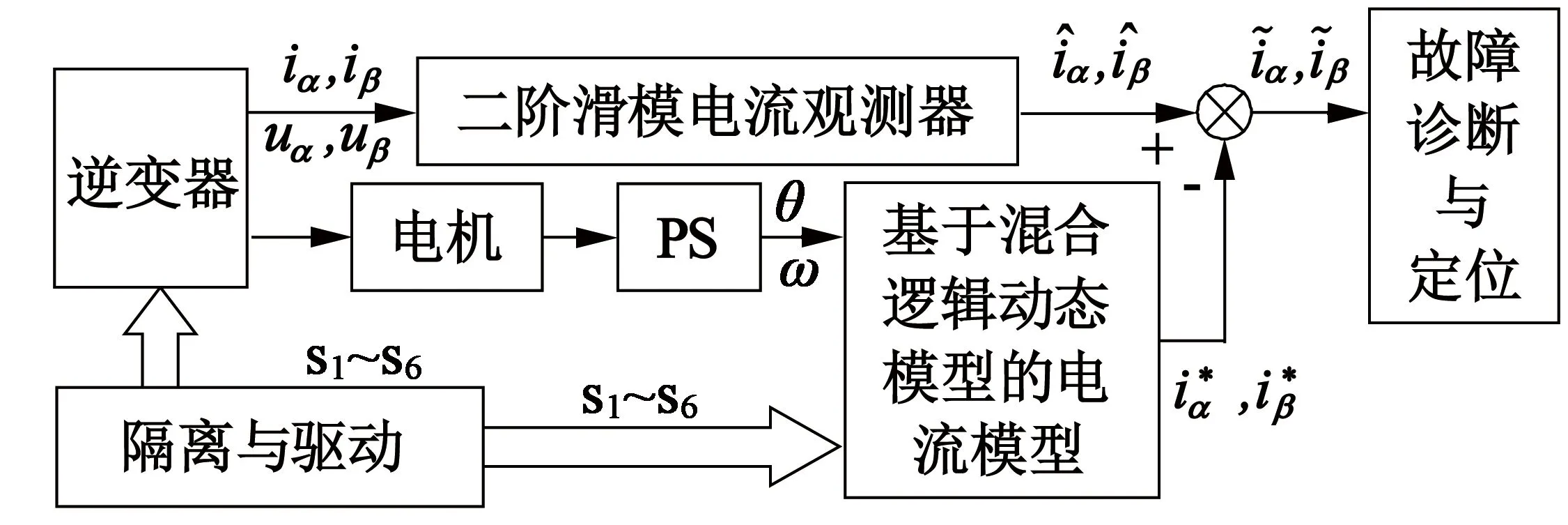
图2基于残差向量的故障诊断原理

将逆变器与PMSM组成一个混合系统，称之为混合逻辑系统。通过s1～s6的取值大小确定系统的拓扑结构和功能约束,结合相电流的方向，对逆变器的工作模式进行分析。根据a相桥臂在不同的故障开关位置以及不同电流方向条件下的工作模式，相电压Uag的数学表达式可表示：

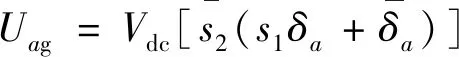
(6)

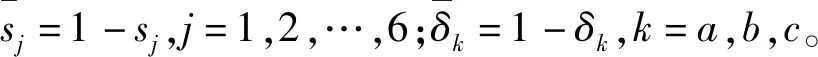
由式(6)便可推出另外两相电压的值：

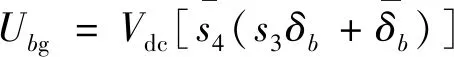
(7)

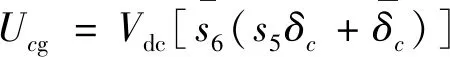
(8)

为了简化三相定子电压表达式，定义一组三维列向量：

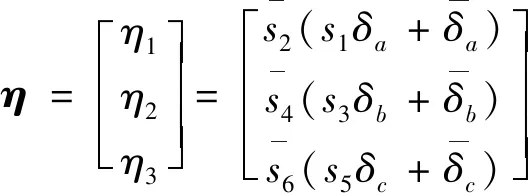
(9)

将式(6)～式(9)代入式(5)，经加减运算得到三相定子电流表达式：

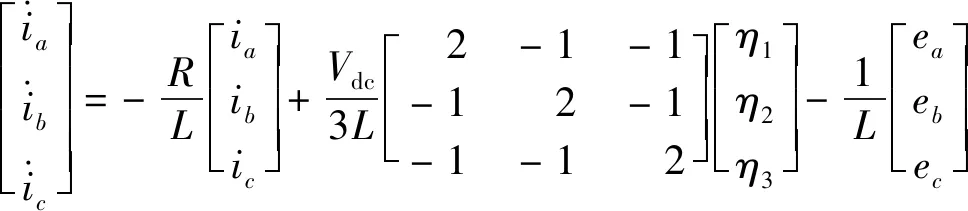
(10)

将式(10)经Clarke变换后便得到三相电流的α轴，β轴分量：

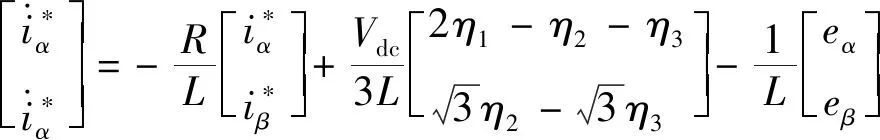
(11)

式(11)即为PMSM驱动系统基于混合逻辑动态模型的电机电流模型，其中反电动势eα和eβ分别如下：

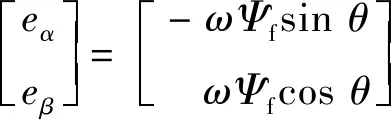
(12)

2 二阶滑模电流观测器

由上文分析可知，PMSM三相电流的α，β轴分量:

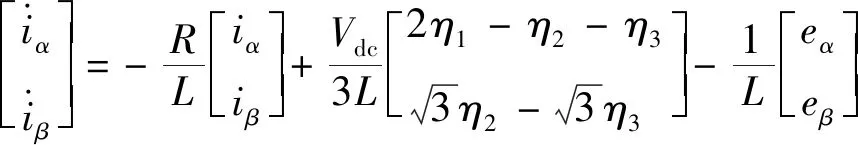
(13)

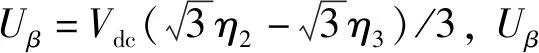
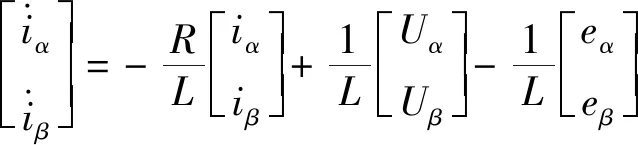
(14)

由式(14)构造一阶滑模电流观测器[15]：

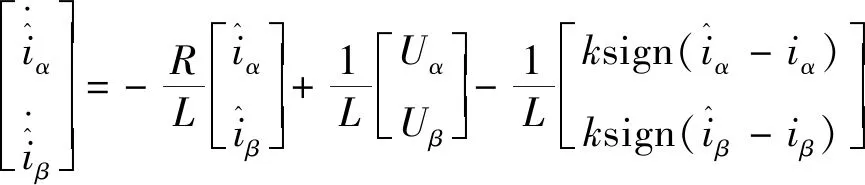
(15)

对式(15)和式(14)作差得一阶滑模电流观测器的误差方程：

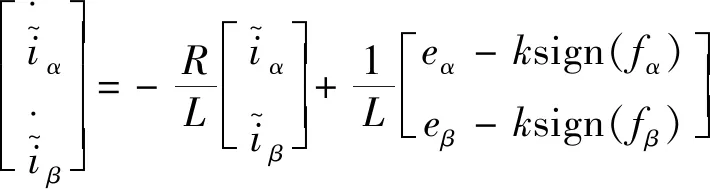
(16)

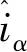
设计二阶滑模电流观测器，如下式：

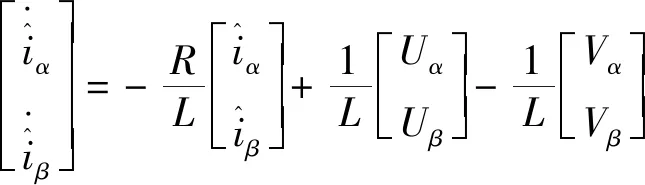
(17)

对式(17)和式(14)作差，得误差方程：

(18)

式中:Vα和Vβ为滑模控制率。

定义Sα和Sβ为二阶滑模切换面，其中:

在上述例句中，我们可以看见英文用了较长的一段句子来表示对方不知道这是他的音乐，还用到了“You’re not the sharpest knife in the drawer”。如果是原文直接翻译的话，那字幕就会变成：“你不是抽屉里最尖锐的刀”。很显然，如果是这样翻译的话，不仅仅句子很长之外，观众还没法了解原文所表达的真正的意思。根据原文的意境，这里是要告诉对方他根本不知道真正的情况，根本都不知道这是他的作品。这个句子直接提取了主要意思，译为“你还不知道，这是他的作品。”即让观众了解了角色所要表达的，又把字幕简约化。这符合字幕翻译的简约性。

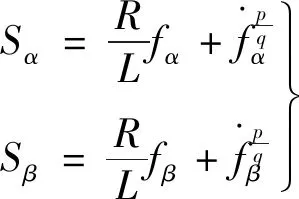
(19)

式中:p，q为奇数，其满足p/q>1。

对式(19)等号两侧求微分，结果如下：

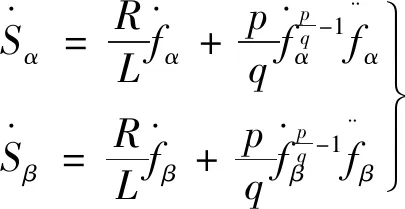
(20)

选择李雅普诺夫函数M=0.5s2，对其求微分，以检验二阶滑模电流观测器稳定性。

(21)

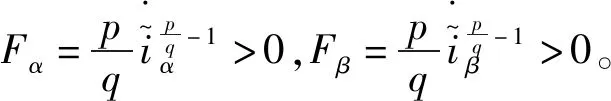
为使得设计的二阶滑模电流观测器稳定，设计滑模控制率Vα和Vβ如下：

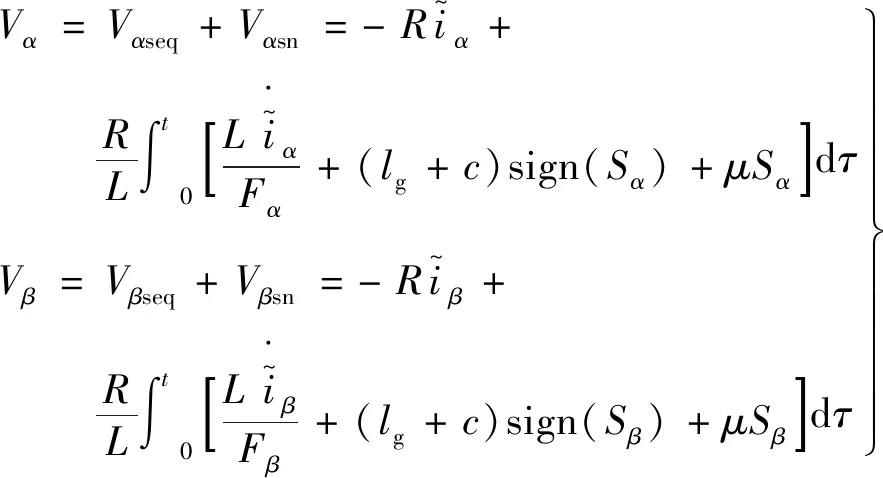
(22)

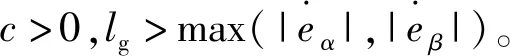
根据文献[16]提出的验证方法，最后可得到:

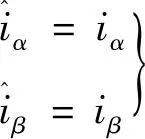
(23)

3 基于电流残差分量和相位角的故障诊断方法

3.1 分析电流残差分量和相位角

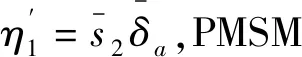
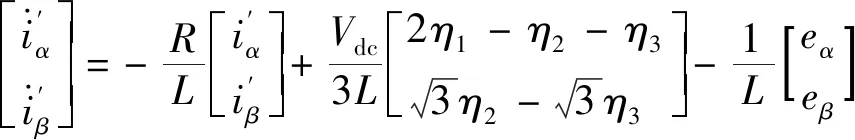
(24)

由上文可知，二阶滑模电流观测器输出量等于实际电机系统的电流值。即此时滑模电流观测器输出量等于桥臂s1故障时的电流值，如下式：

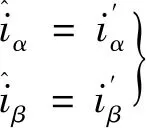
(25)

对式(24)求微分，得:

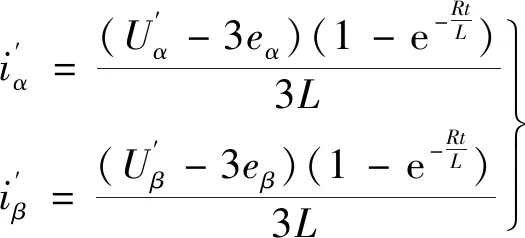
(26)

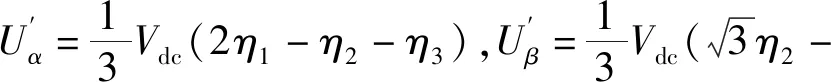
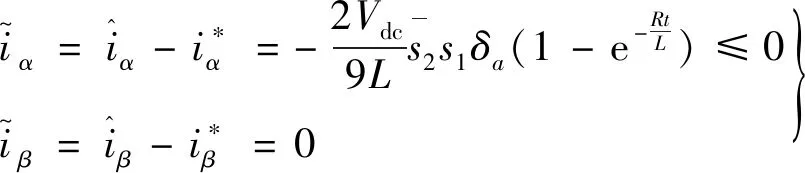
(27)

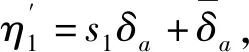
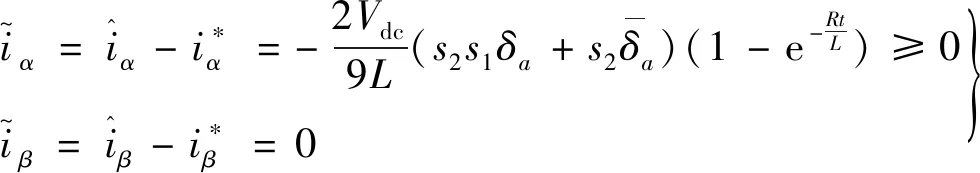
(28)

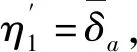
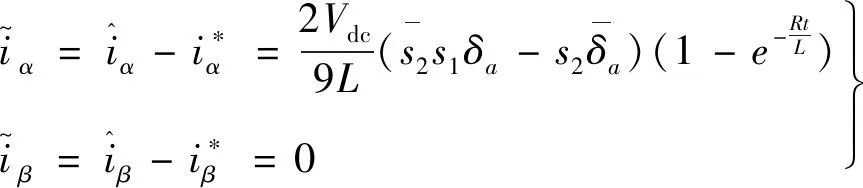
(29)

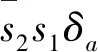
定义电流残差矢量表达式：

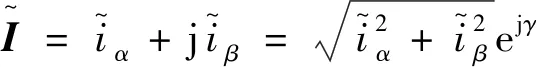
(30)

将式(27)～式(29)分别代入式(30)，可得到电流残差相位角γ。γ1=0，γ2=0，γ3=0或180°。b，c相桥臂发生开路故障时的分析过程与a相桥臂相似，分析过程不再一一叙述。

3.2 对故障开关进行定位

将所有电流残差分量根据式(30)求出各自相对应的幅值，分别表示在二相静止坐标系中，便得到电流残差矢量轨迹图，如图3所示。

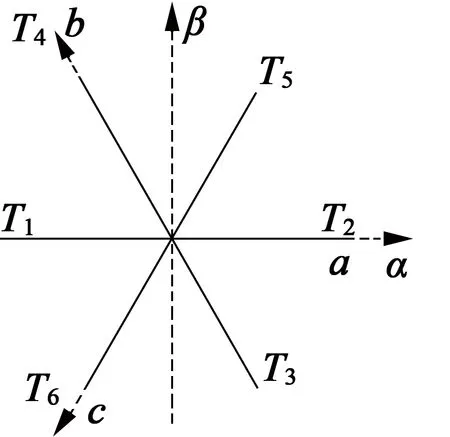
图3电流残差矢量图

当无故障时，电流残差矢量处于原点位置。当a相桥臂发生开路故障时，若s1关断，电流残差矢量轨迹则向T1方向运动；若s2关断，电流残差矢量轨迹则向T2方向运动；若s1和s2同时关断，电流残差矢量轨迹则沿a轴正负方向运动。b，c相桥臂发生开路故障时与a相类似，b相桥臂的电流残差矢量轨迹对应T3T4方向，c相桥臂的电流残差矢量轨迹对应T5T6方向。

3.3 确保故障检测方法的鲁棒性

图3中的电流残差矢量轨迹，在理想条件下才可实现，在实际系统中，由于测量误差、噪声等因素影响，电流残差矢量轨迹将偏离故障相轴，在故障相轴附近运动。除了不会完全沿故障相移动，即使在正常状态(即非故障状态)下，电流残差矢量虽接近于零，但仍会呈现一定的幅值和相位。因此，如果该方法直接用于诊断故障，系统将不会有较高的鲁棒性。

因为存在测量误差、系统噪声等影响，设置阈值Ith来避免诊断过程中出现的误判。设定阈值的大小为额定电流，这样当电流残差矢量的幅值大于阈值时，才可判定检测到故障。然后，为了当电流残差矢量轨迹在故障相轴附近运动时，也能诊断出故障，将矢量平面平均划分为6个扇形区域Ⅰ～Ⅵ，故障相轴在每个扇形区域的中间，如图4所示。轴定位在每个扇区的中间，以提高诊断方法的可靠性和鲁棒性。电流残差矢量轨迹所在的扇区及其相应的故障开关如表1所示。

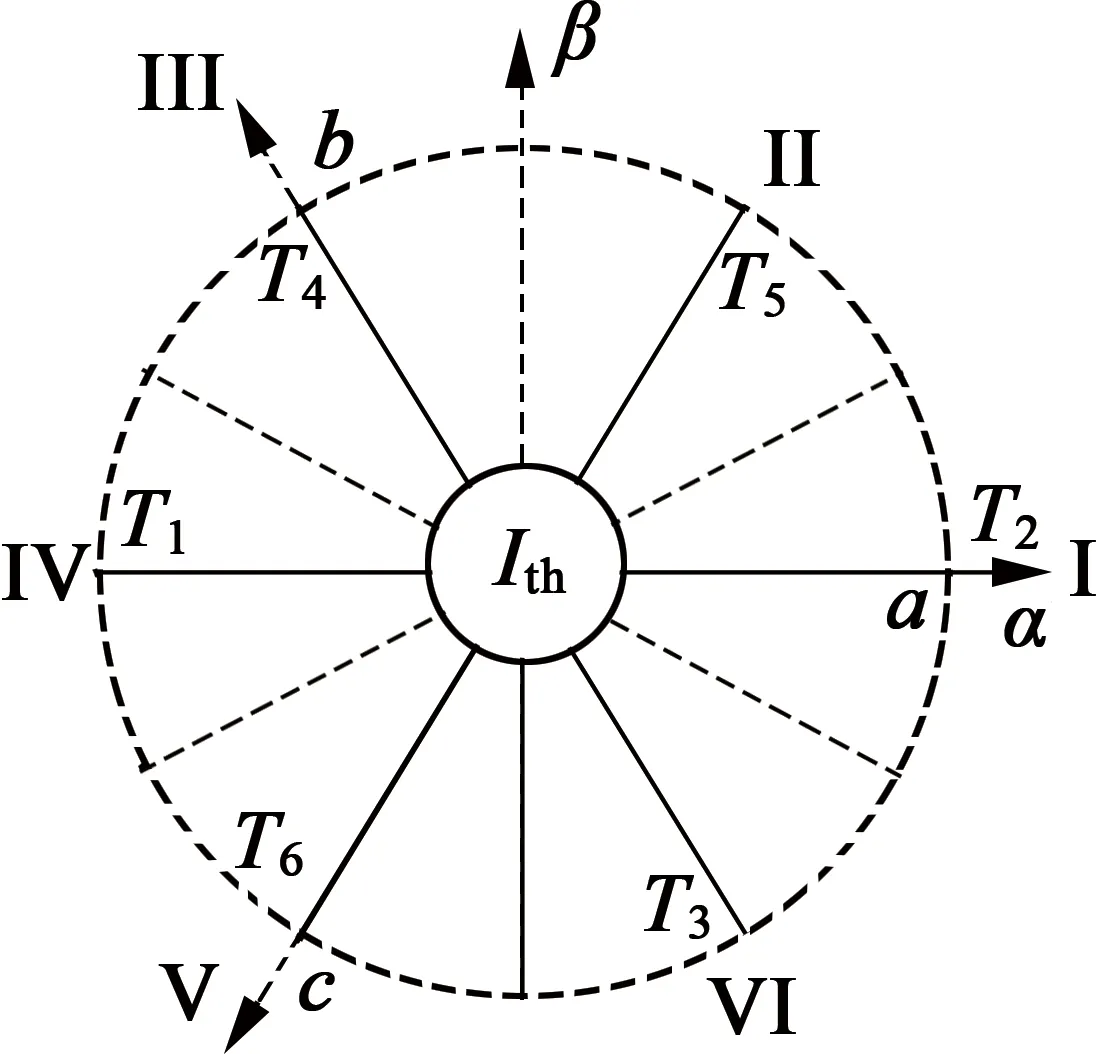
图4 电流残差矢量轨迹扇区分布图

4 实验仿真

为检测本文诊断方法的可行性，利用MATLAB/Simulink建立了磁场定向矢量闭环控制的PMSM驱动系统及其混合逻辑动态模型。根据图2构造了基于残差矢量的逆变器开路故障诊断模型，电机参数如表2所示，0.06 s时发生开路故障。在图5至图7中列出了逆变器桥臂a上开关发生开路故障的仿真结果。

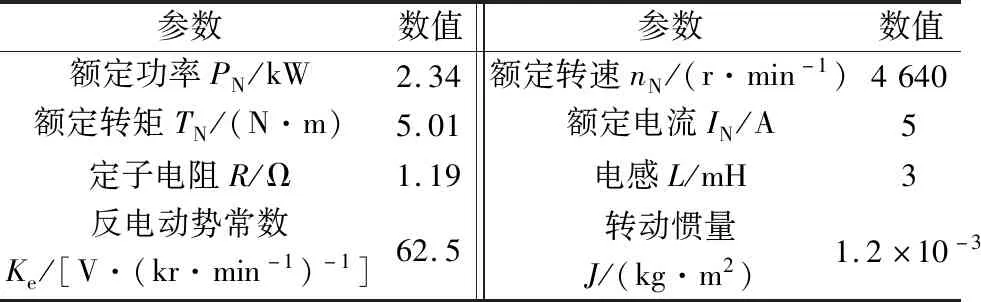
表2 电机参数

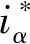
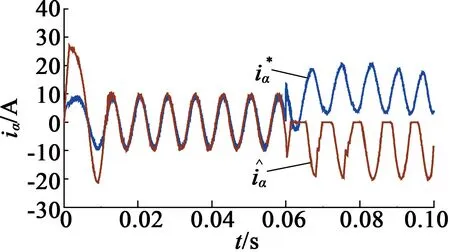
与的对比图

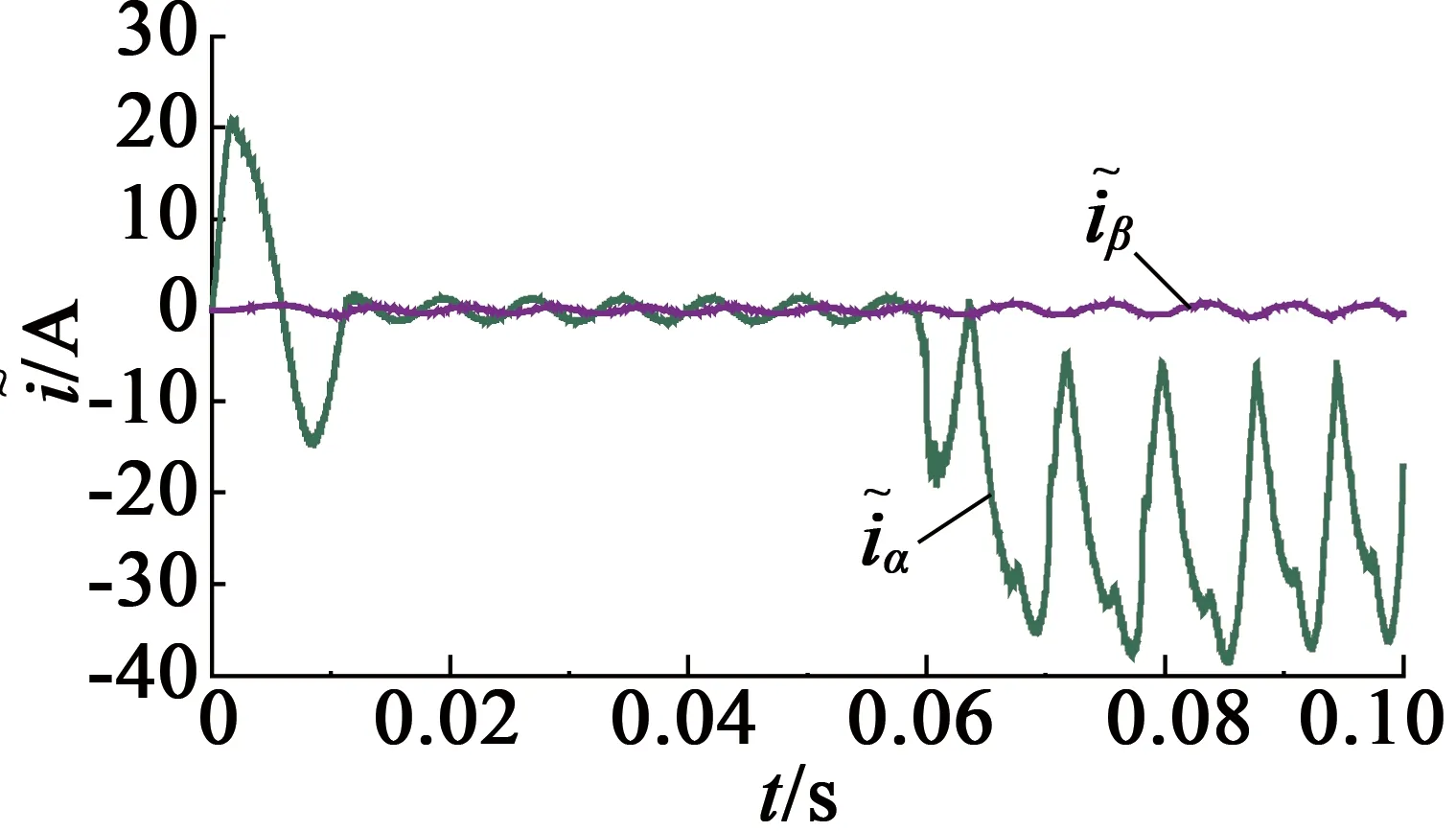
与对比图

(c) 电流残差矢量轨迹

图5s1发生开路故障时的仿真图

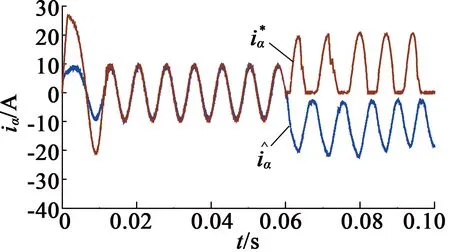
与的对比图

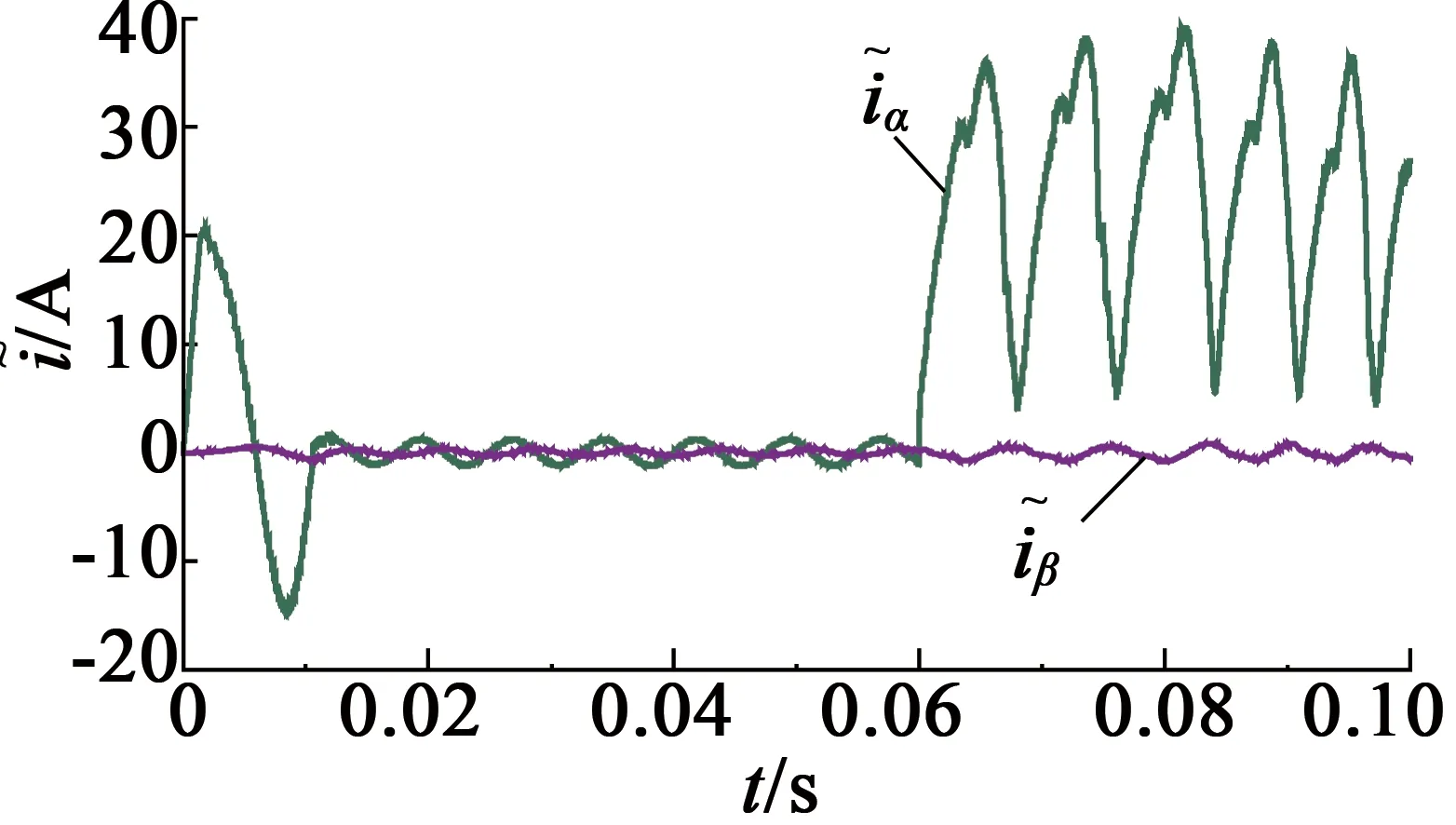
与对比图

(c) 电流残差矢量轨迹

图6s2发生开路故障时的仿真图

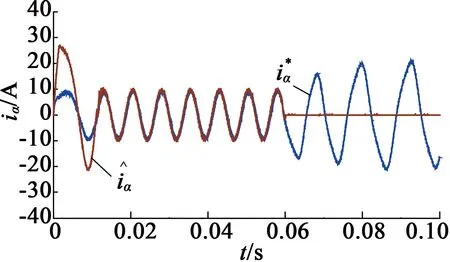
与的对比图

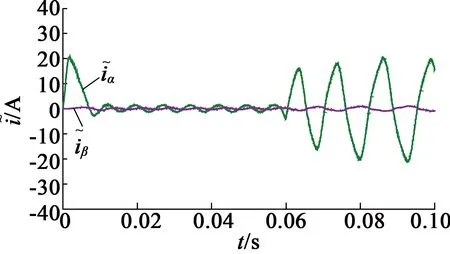
与对比图

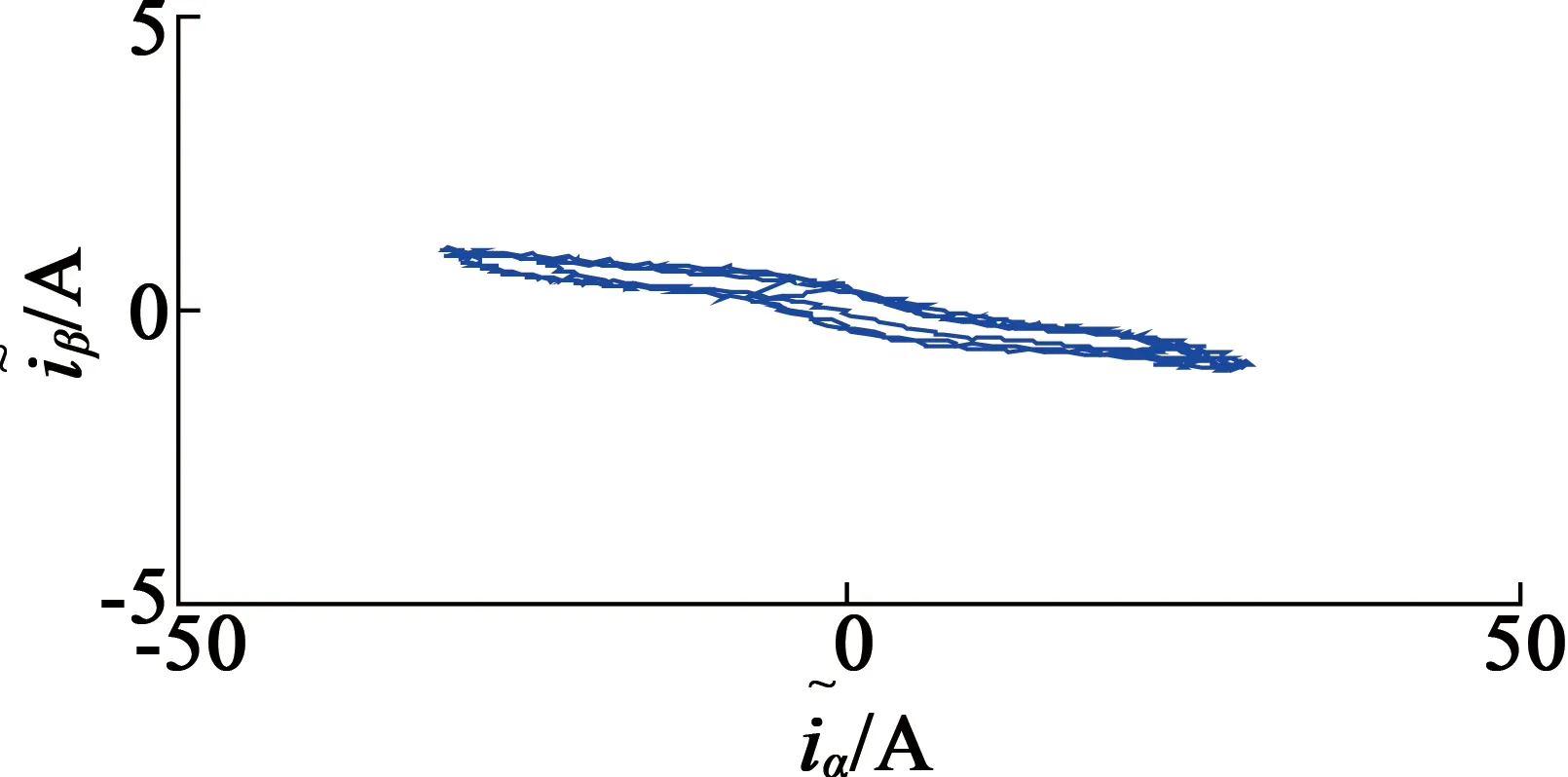
(c) 电流残差矢量轨迹

图7s1,s2同时发生开路故障时的仿真图

5 结 语

本文研究了PMSM驱动系统基于二阶滑模电流观测器和混合逻辑动态模型的电流残差矢量的故障诊断方法。本文的故障诊断策略较其他基于电流信息的诊断策略优势如下：该诊断策略与现有电流故障诊断策略相比，诊断时间缩短至四分之一个周期以内；为了诊断策略的可靠性以及观测值的精度，省去了额外的传感器，通过构建二阶滑模观测器以观测电流值，在保证精度以避免观测值相位滞后的同时，还可有效抑制抖振；该方法可以消除负载对系统闭环控制算法的影响，具有较好的可靠性和鲁棒性，不论单开关或多开关的开路故障均能正确检测出，有效降低了系统的复杂性与成本。