永磁同步电机有限时间混沌同步控制
2019-09-04刘加勋王佐勋雷腾飞尹万军
刘加勋,王佐勋,雷腾飞,尹万军
(1.齐鲁工业大学,济南 250353;2.齐鲁理工学院,济南 250200;3.国家电网章丘区供电局,济南 250200)
0 引 言
1990年,美国海军实验室的学者Pecora和Carroll[1]提出了混沌同步控制方法,并且在电子电路中实现了混沌同步。混沌同步就是对混沌系统加以控制,使其轨迹逐渐逼近另一混沌系统轨迹。随着电力电子技术与工程控制技术的发展,混沌现象被广泛发现于永磁同步电机、无刷直流电机、开关磁阻电机等伺服系统之中,引发了国内外广大学者的研究热潮。1994年Hemati[2]发现了永磁电机开环驱动系统中存在着混沌现象。张波[3]等人给出了其通用模型,并对其进行了更深入的研究。永磁同步电机作为一种强耦合、非线性、多变量系统,其在发生混沌现象时所表现出的主要特征是随着电机性能参数的变化,系统会发生转矩以及转速的不稳定,控制性能明显降低,出现电磁噪声等一系列对系统控制有害的影响,继而出现了混沌抑制问题;从另一个方面来说,电机产生的混沌行为在一些特定的场合,比如在原材料的研磨与搅拌方面是非常有益的,这就产生了混沌反控制问题。
目前,关于电机混沌同步的研究还是比较少的,尚且处于初步阶段。文献[4]运用了模糊控制原理对系统参数不确定的永磁同步电动机系统进行了混沌同步;文献[5]基于主动控制原理将永磁同步电机分别与Arneodo与Duffing系统进行异结构同步;文献[6]遵循Lyapunov稳定性理论,将Lorenz系统分别与Chen系统和Rossler系统进行异结构同步,并且对其在保密通信中的应用进行了探究;文献[7-9]基于自适应原理对非均匀气隙的永磁同步电机进行了混沌同步;文献[10]基于最优控制理论与Pontryagin 极小值原理对非均匀气隙的永磁同步电机进行了混沌控制。
模糊控制容易降低系统控制精度以及动态性能;最优控制理论需要系统参数满足一定的条件,并且算法优化存在一定的复杂性;自适应同步法通过引入自适应机制实现系统的控制,但是自适应的引入容易增加系统的开支,会对系统的响应能力产生影响;传统基于主动控制原理的同步方法控制能力还需要进一步加强。
还有一个问题,就是许多关于混沌同步控制的文献[4-10],仅仅考虑了系统整体同步的鲁棒性,并没有从有限时间的观念出发去设计控制器,考虑到有限时间混沌同步的文献[7-8],其同步的时间还能够进一步优化。
本文在文献[5]控制原理的基础上,基于Lyapunov稳定性理论、有限时间稳定理论,设计了一种新型带有终端吸引子的主动控制器,实现了永磁同步电机有限时间混沌同步。
1 永磁同步电机混沌数学模型
为不失一般性,永磁同步电机模型参考文献[11]中的混沌数学模型,如下所示:
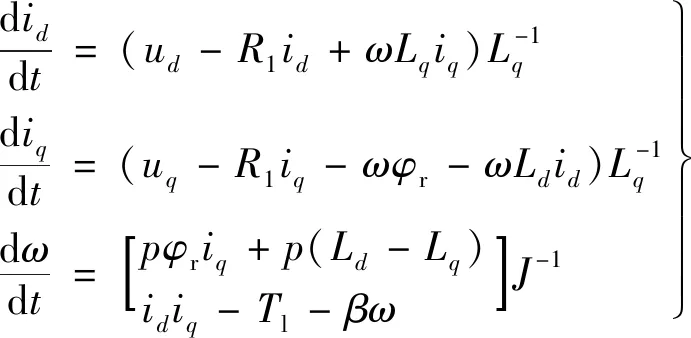
(1)
式中:id与iq是定子电流的直轴与交轴分量;ω是转子角频率;Tl是外部转矩;J是转动惯量;β是黏性阻尼系数;R1是定子绕组;Ld与Lq是d,q轴定子电感;p是电机极对数;φr是永久磁通;ud与uq是定子电压的直轴与交轴分量。
对式(1)继续处理有:
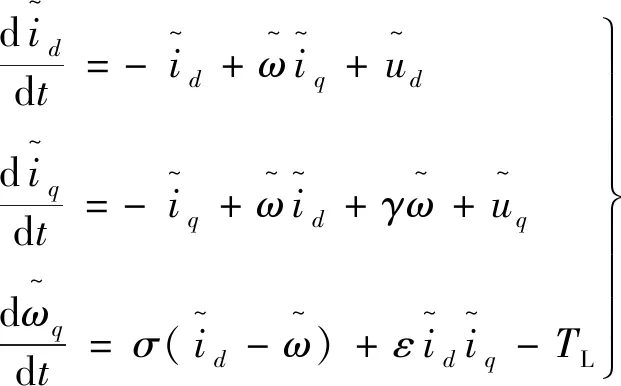
(2)
此处只考虑气隙均匀,即:
此时能够得到永磁同步电机的数学模型:
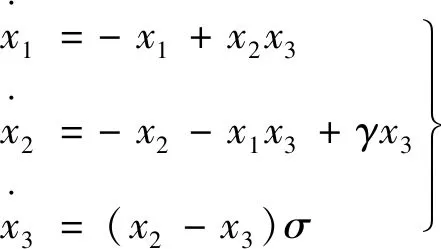
(3)
当γ=20,σ=5.46时,系统会呈现出混沌状态,其系统相图如图1所示。
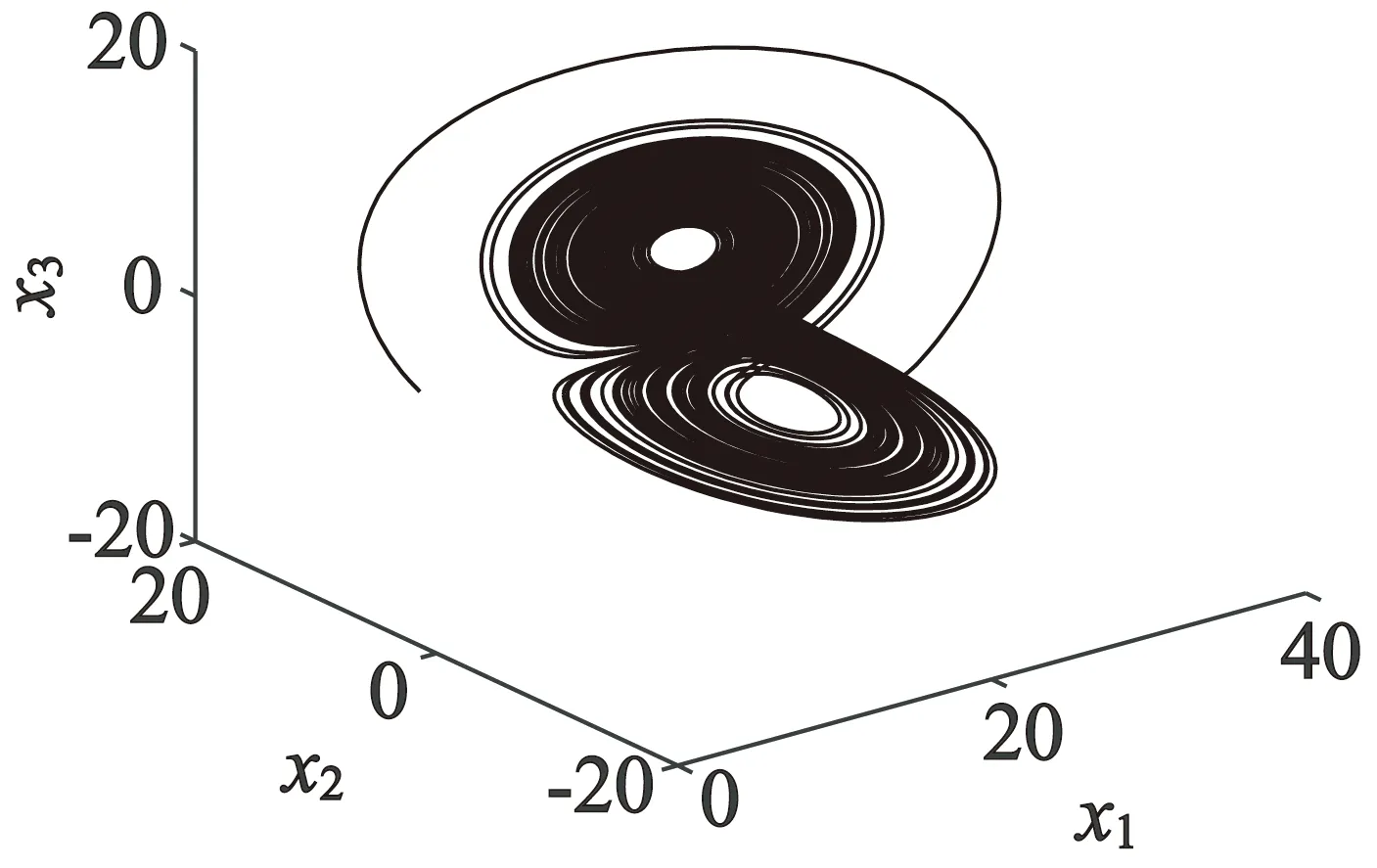
图1 永磁同步电机奇怪吸引子图
改变永磁同步电机数学模型x1与x2的顺序,可以得:
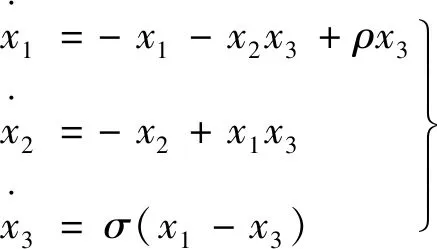
(4)
当σ=5.46,ρ=20时,式(4)处于混沌状态,其系统相图如图2所示。
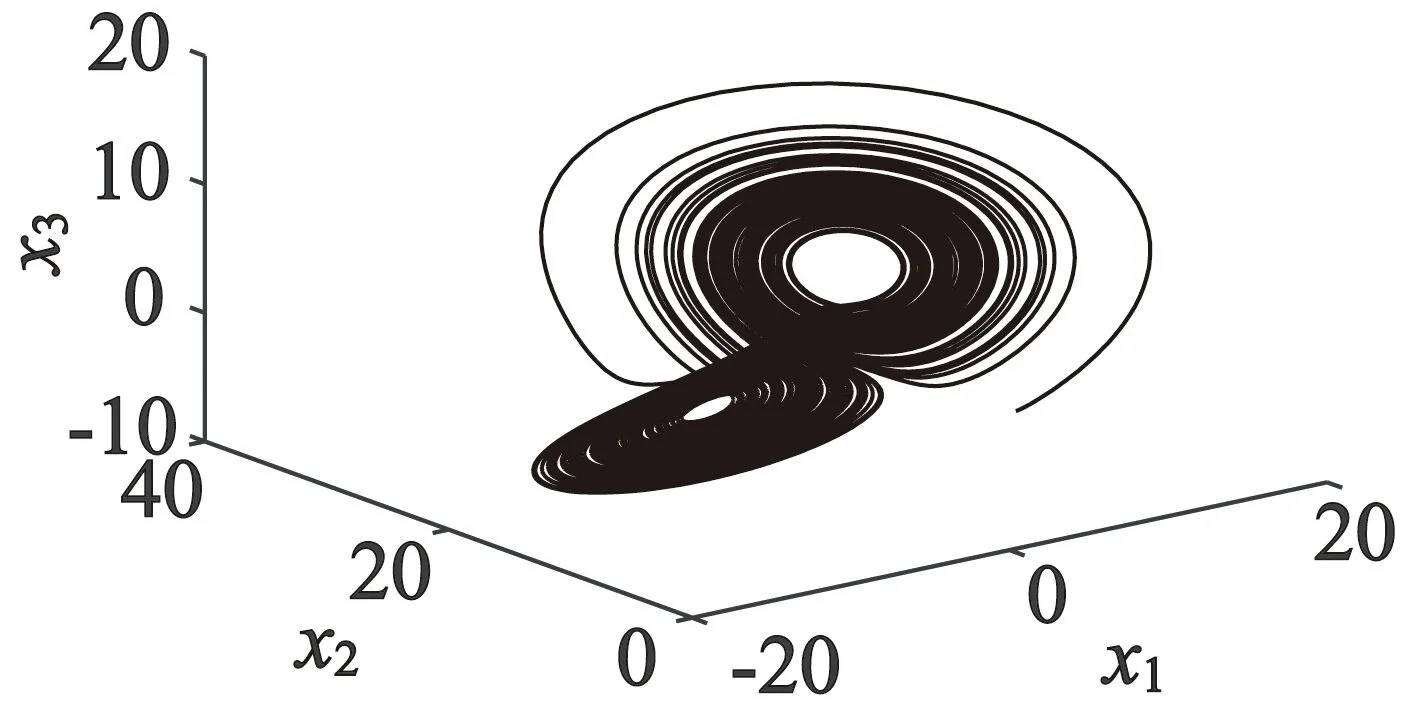
图2 式(4)奇怪吸引子图
2 永磁同步电机有限时间混沌同步
2.1 有限时间稳定理论
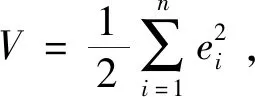
2.2 控制器设计以及系统同步
为了实现永磁同步电机系统与式(4)系统的同步,本文使用驱动-响应同步法对系统进行同步,设驱动系统为式(4)系统,响应系统为永磁同步电机系统:
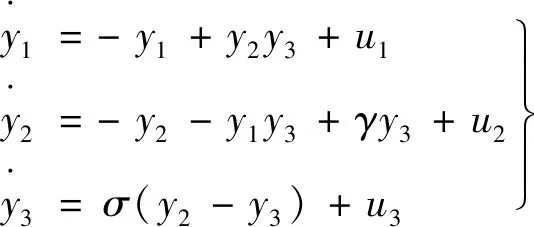
(5)
u1,u2和u3就是我们所期望的控制函数。设:
e1=y1-x1,e2=y2-x2,e3=y3-x3
则可以得到误差系统:
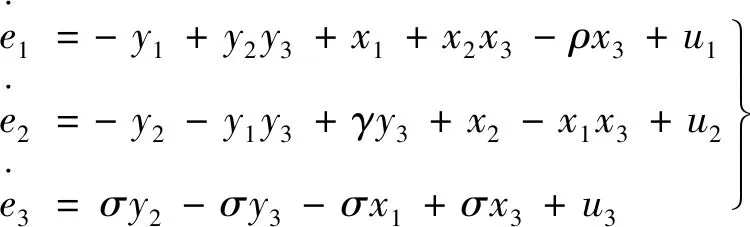
(6)
定理2:定义控制函数u1,u2和u3,
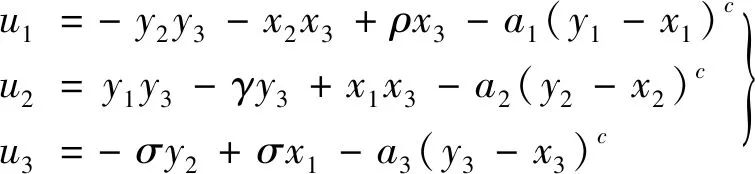
(7)
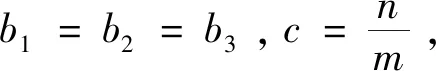
由此选择Lyapunov函数:
对V求解关于t的导数:
将式(7)代入式(8)中,可以得到:
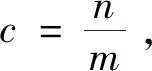
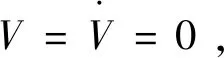
综上所述,式(6)系统在加入控制器式(7)后,其状态误差会在有限时间内逐渐趋于零,从而也就说明了驱动系统与响应系统在有限时间内达到了同步。
3 仿真结果
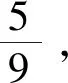
首先应用文献[4]中控制器在本文系统中可有:
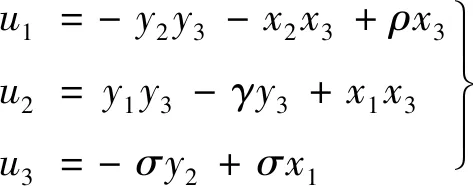
(10)
从控制器的形式可以看出,它仅是把原误差系统中的非线性项去掉,也没有提供可以调节的参数,对系统的控制能力较为单一。而本文控制器的设计引入一个新型可调节参数与分数阶次幂,提高了对误差系统的控制能力,也不会增加系统的支出,对比结果仿真结果如图3~图6所示。
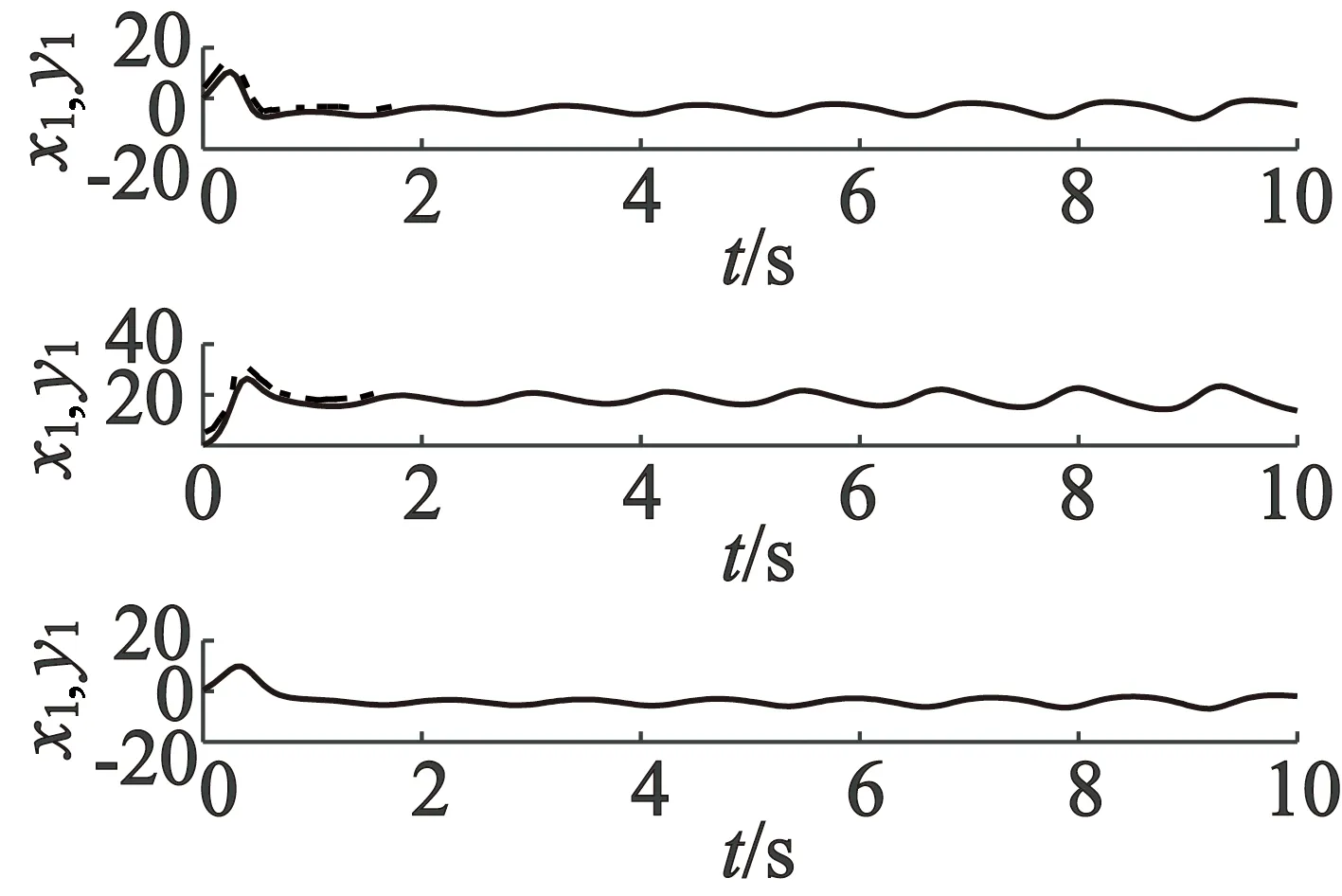
图3 文献[4]中永磁同步电机与式(4)系统状态同步图
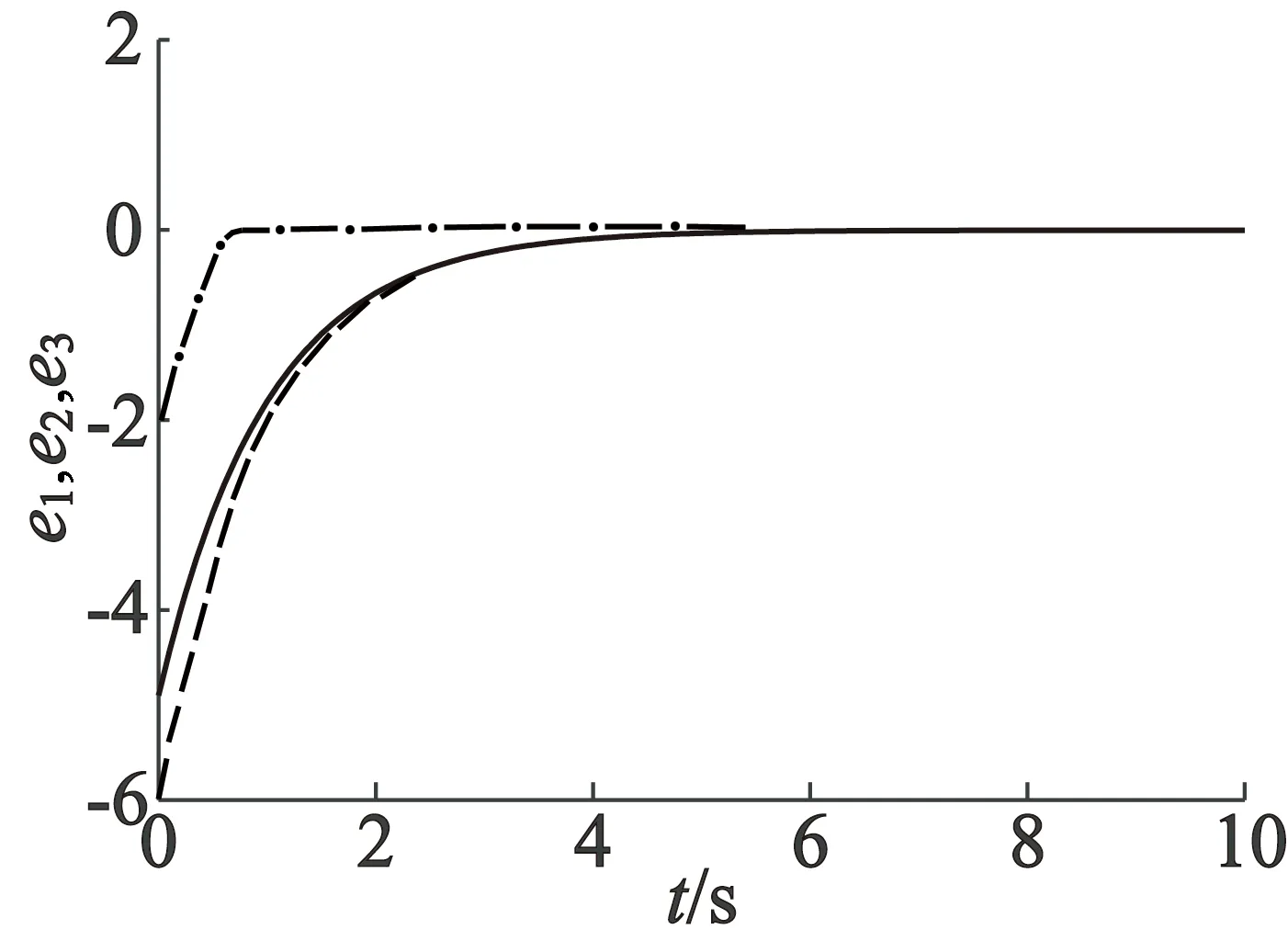
图4 文献[4]中永磁同步电机与式(4)系统同步误差图
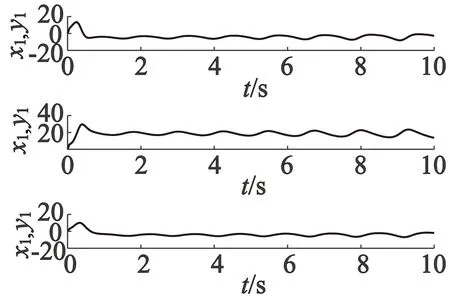
图5 本文永磁同步电机与式(4)系统状态同步图
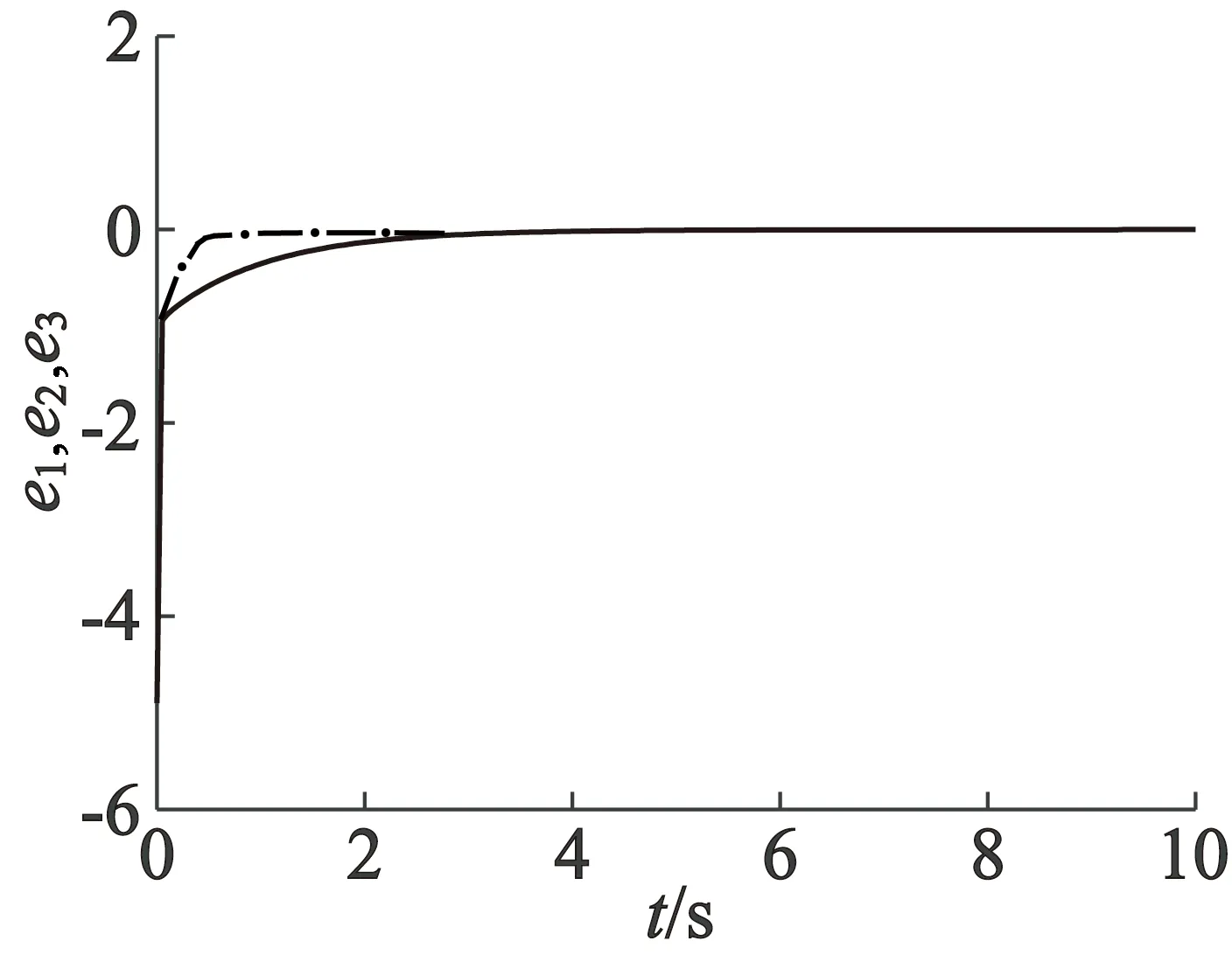
图6 本文永磁同步电机与式(4)系统同步误差图
由以上同步图得到,文献[4]原理控制器需要6s左右系统能够完全达到同步;本文原理控制器在3 s左右系统就能完全达到同步。再者,由于参数可调,同步时间还可以人为调节以达到期望的效果。由此充分说明了本文混沌同步控制器的优越性。
4 结 语
本文基于Lyapunov稳定性理论与主动控制原理,给出了一种永磁同步电机的有限时间混沌同步控制策略。该方法由于分数次幂项与可调节系数的存在,大大缩短了同步时间,提高了系统的响应能力,并且不会增加系统的支出。通过仿真与传统控制策略比较,验证了本文控制方法在同步时间上更具有优越性以及快速响应能力。为永磁同步电机有限时间混沌同步的研究提供了参考,在实际工程中具有较好的应用价值。
