基于Benford-SVR的数据异常检验模型构建及其应用

李斐斐 周向阳 秦朗 葛章明 韩书庆 张晶 吴建寨

摘要：当前数据数量剧增的同时，大量异常数据的存在降低了数据质量，数据分析工作面临着数据丰富而信息贫乏的困境，寻找有效的数据异常检验模型，成为数据科学研究的重要内容。本研究以农业生产数据为对象，融合应用Benford定律与SVR模型的技术优势，构建Benford-SVR异常数据检验模型，并以河北省7个地市131个县为例进行实证分析。结果表明，沧州、邢台、邯郸的数据集质量较好，保定、石家庄、唐山、张家口数据集质量较差，并从中有效挖掘出异常较大的数据点。本研究结果为农业数据应用与信息提取提供了参考，Benford-SVR模型可以作为数据质量检验中精准挖掘异常點的有效工具。

关键词：数据质量;Benford定律;SVR;农业生产数据

中图分类号：S126：TP393文献标识号：A文章编号：1001-4942（2019）07-0136-07

近年来数据资源量剧增的同时，数据质量问题引起了各界高度重视[1]，去冗分类、去粗取精，提高数据质量成为当前主要任务[2，3]。已有研究表明，当前海量数据中不仅存在着许多冗余、缺失、一致性差等问题，还充斥着大量异常数据。这些异常数据并不完全是错误数据，而是指数据集中与众不同的数据，让人怀疑这些数据并非随机偏差，而是产生于完全不同的机制[4，5]。基于这种思想，从大数据池中寻找异常数据，提升数据质量，逐渐成为数据科学的一个重要方向，学者们不断提出基于统计[6]、距离[7]、密度[8]、聚类[9]、BP神经网络[10]等校验与挖掘的算法，并应用到经济、金融、地理、交通等领域。

Benford定律由Simon Newcomb于1881年发现，后在1938年经Benford再次提出引起学术界重视，现已被广泛应用于异常数据的检验中[11]。Benford定律最早被用于网络入侵[12]、生物生理[13]等自然科学领域数据的检验，近年来在会计[14]、统计[15]、财务[16]、保险[17]等社会科学领域的数据检验中亦取得了较好效果。Benford定律研究的重点是数据准确性，而非探究数据背后存在的问题。而支持向量机（support vector machine，SVM）能够攻克“过学习”、“欠学习”、“维数灾难”等一些异常数据挖掘中的典型困难[18]，已有研究表明，基于SVM的SVR（support vector regression）模型具备总体残差较小、鲁棒性高的特点，且能有效发现异常数据点[5，19]。

本研究融合两个模型的优点，构建了Benford-SVR异常数据检验模型，并以河北省农业数据进行了实证分析，为数据质量校核及相关研究工作的开展提供支持与参考。

1 材料与方法

1.1 基础理论

1.1.1 Benford定律 Benford定律也被称为“首位数定律”，它指出在自然界中数据集中的第一位非零有效整数的统计概率满足对数分布。在数学上，Benford定律是唯一具有标度不变性的数位定理[20]。Benford定律首数字为1～9的分布概率如公式（1）所示：

由图1可知，数字1～9在第二位、第三位的概率都是单调递减的。根据数字的联合分布函数和乘数法则，可以推导出各数位的条件概率如公式（2）所示：

1.1.2 显著性检验方法 数据的形成受多种外界因素影响，对首位数统计结果进行显著性检验在一定程度上可以避免随机误差干扰。假设检验的原假设和备择假设如下：

原假设H0 ：样本数据集的首位数（更高位数字）统计结果服从Benford定律分布;备择假设H1：样本数据集中首位数（更高位数字）统计结果不服从Benford定律分布。

常用的方法有四种：χ2拟合优度检验、修正K-S拟合优度检验、距离测量检验、相关系数检验[21]。考虑到统计量受样本量影响较大，综合分析各检验方法特点，当样本量不大时，使用χ2、VN对结果进行判定;当样本量较大时，使用相关系数r对结果进行判定。

表1给出统计量χ2、VN*临界值情况，其中α表示显著水平。

（3）Pearson相关系数：是衡量两个数据集之间相关关系的重要统计量，其判断标准如表2所示。

1.1.4 核函数 在支持向量回归过程中，核函数能将原始数据映射到高维特征空间，从而避免原始数据集进行复杂非线性变化时可能发生的“维数灾难”，极大提高支持向量回归效率。核函数变换如图2所示。

在统计学中，任意满足Mercer定理的函数都可以作为核函数，从而实现高维映射。常用的有高斯径向基函数、多项式核函数、Sigmoid核函数、样条核函数4种，其中，径向基（RBF）函数可以将数据映射到无穷维，解决大部分支持向量回归问题[23]，是最常用的核函数之一，具体形式如下：

1.1.5 粒子群算法 核函数中的参数对回归效果有很大影响，需要用优化算法获取最优值。常用的优化算法有网格搜索法、遗传算法和粒子群算法等，其中，粒子群（PSO）算法简单、搜索速度快、效率高，在求解最优参数过程中具有明显优势，应用范围最广[24，25]。粒子群算法数学描述为：

1.2 模型构建

综合利用Benford定律和SVR建立组合模型，其中，SVR模型选取RBF核函数，优化算法采取PSO算法。Benford-SVR模型处理流程如图3所示。

1.3 数据来源与处理

1.3.1 数据获取 以农业GDP为分析数据对象，选取2000、2005、2010、2015年河北省石家庄、邯郸、邢台、沧州、张家口、唐山、保定7个市131个县的农业生产数据进行研究。同时，为了试验准确性，引入农用化肥、农作物总播种面积、农业机械总动力、农业劳动力、有效灌溉面积、农业固定资产投资额等作为关联验证数据。数据来源于《中国县域统计年鉴》。

1.3.2 数据预处理 首先，采用线性插值法对缺失数据进行填补，得到可用数据集;其次，采用主成分分析法（PCA）进行关键指标选取，确定农用化肥、农作物总播种面积、农业机械总动力、农业劳动力、有效灌溉面积五个指标作为在农业GDP研究过程中的重要输入向量。

2 结果与分析

2.1 异常数据池筛选

2.1.1 整体样本检验 样本集数据首数字的频率分布如表3所示。可知，数据集实际频率与Benford频率分布趋势基本一致，只有首数字为2时有明显差别。因为数据集为小样本数据，在显著水平为0.05条件下，χ2统计量为18.056，大于自由度为8时的临界值15.51，数据真实性较可疑。

2.1.2 时间维度检验 分别统计2000、2005、2010、2015年4组数据集的首数字频率分布，结果显示，首数字“2”的频率与相应的Benford频率有明显差别（表4）;在显著性水平0.05条件下，这4组数据的χ2统计量都小于自由度为8时的临界值15.51，数据集质量较高（表5）。

2.1.3 空间维度检验 分别统计沧州、邢台、邯郸、保定、唐山、张家口、石家庄7组数据集的首数字频率分布，结果显示，数据集首数字的频率与相应的Benford频率有明显差别（表6）;在显著性水平0.05条件下，对数据集进行拟合优度检验，保定、张家口、石家庄的χ2统计量都大于15.51，而唐山的Pearson相关系数仅为0.931（表7），这四组数据集存在异常数据可能性较大。

综上，沧州、邢台、邯郸的数据集质量较好，保定、唐山、张家口、石家庄数据质量较差，属于异常数据池。这个异常数据池范围较大，难以直接从中精确挖掘异常点，所以需要用SVR进一步处理。

2.2 异常数据点挖掘

通过样本检验已知，沧州、邯郸、邢台的数据集质量较好，而保定、石家庄、唐山、张家口数据集异常可疑性较大。基于此，初步选取沧州、邯郸、邢台作为训练集，共184个样本;而唐山、保定、张家口、石家庄四个市的数据作为测试集，分别包含40、88、52、68个样本。

2.2.1 确定训练集 从沧州、邯郸、邢台的184个样本中选取160个样本点作为训练集，另外24个样本点作为预测集。用粒子群算法优化参数对（C，g），优化结果为C=1.4142，g=0.8284，带入SVR模型中进行分析，结果（图4）显示，模型的MSE=0.0061，决定系数R2=0.9175，预测值和真实值差别较小，确定该样本集可以作为训练集。

2.2.2 异常数据挖掘 以沧州、邯郸、邢台的184个样本作为训练集，分别选择唐山、保定、张家口、石家庄的样本作为预测集，用粒子群算法优化参数C、g，并分别带入SVR模型中进行训练，再对五个地区的数据集进行异常分析。

由图5可见，唐山数据集的MSE=0.0189，决定系数R2=0.8640，数据集误差变大，回归效果变差，数据集中许多样本点的预测值和真实值存在差异，异常表现较大的10个点序号依次为189、205、157、211、195、199、185、20、213、187。

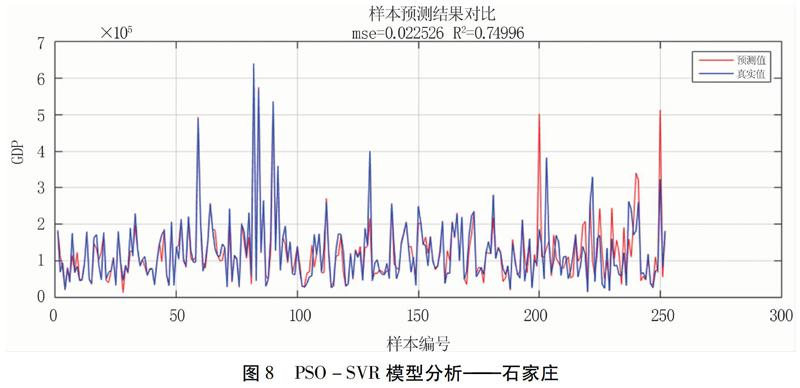
保定数据集的MSE=0.0147，决定系数R2=0.8033，异常表现最大的10个点序号依次为81、270、165、185、265、152、264、87、240、258（图6）;张家口数据集的MSE=0.0084，决定系数R2=0.8687，异常表现最大的10个点序号依次为193、143、222、71、208、83、196、209、216、187（图7）;石家庄数据集的MSE=0.0225，决定系数R2=0.7500，异常表现最大的10个点序号依次为226、200、19、194、202、212、227、147、236、233（图8）。

3 讨论与结论

本文在研究了Benford定律和支持向量回归（SVR）不同特点的基础上，充分利用两者的技术优势，构建了Benford-SVR异常数据检验的组合模型。从对河北省7个市131个县生产数据集进行实证分析的结果看，该模型可以通过甄别数据集的数据质量，挖掘出影响数据质量的最大可疑异常点。

在当前大数据迅猛发展的背景下，数据质量的重要性更加突出，数据质量检验的研究也越来越受到重视。但研究不应仅停留在对数据质量的判定上，还应能有效找到“污数据”，这样才对实践管理工作中的数据校核、研究工作中的缺失数据插值等更具有价值[2，17]。Benford定律和SVR模型都是基于数据客观分布规律开展分析，没有考虑数据代表的意义或所在行业属性[15，18]，只能在大数据背景下才有效。当前，数据检验模型在农业中的应用较少，虽然Benford-SVR异常数据检验模型已经展现出了可行性，但还需进一步研究和完善，如对异常点数据的处理以及针对行业属性特点开展针对性的模型等。

参 考 文 献：

[1]杨青云，赵培英，杨冬青，等. 数据质量评估方法研究[J]. 计算机工程与应用， 2004（9）：3-4，15.

[2]李国杰，程学旗. 大数据研究：未来科技及经济社会发展的重大战略领域——大数据的研究现状与科学思考[J].中国科学院院刊， 2012， 27（6）：647-657.

[3]许世卫，王东杰，李哲敏. 大数据推动农业现代化应用研究[J]. 中国农业科学， 2015， 48（17）：3429-3438.

[4]黄守坤. 异常数据挖掘及在经济欺诈发现中的应用[J]. 统计与决策， 2003（4）：32-33.

[5]王雷，张瑞青，盛偉，等. 基于支持向量机的回归预测和异常数据检测[J]. 中国电机工程学报， 2009， 29（8）：92-96.

[6]梁昇，肖宗水，许艳美. 基于统计的网络流量异常检测模型[J]. 计算机工程， 2005（24）：123-125.

[7]赵泽茂，何坤金，胡友进. 基于距离的异常数据挖掘算法及其应用[J]. 计算机应用与软件， 2005（9）：105-107.

[8]赵春晖，王鑫鹏，闫奕名. 基于密度背景纯化的高光谱异常检测算法[J]. 哈尔滨工程大学学报， 2016， 37（12）：1722-1727.

[9]朱燕，李宏伟，樊超，等. 基于聚类的出租车异常轨迹检测[J]. 计算机工程， 2017， 43（2）：16-20.

[10]马黎，赵丽红，傅惠.基于BP神经网络的交通异常事件自动检测算法[J].交通科技与经济， 2010， 12（6）：47-50.

[11]Benford F.The law of anomalous numbers [J]. Proceedings of the American Philosophical Society， 1938， 78（4）：551-572.

[12]Arshadi L， Jahangir A H. Benfords law behavior of Internet traffic[J]. Journal of Network and Computer Applications， 2014， 40：194-205.

[13]de Vries P， Murk A J. Compliance of LC50 and NOEC data with Benford[KG-*3]s law： an indication of reliability [J]. Ecotoxicology and Environmental Safety， 2013， 98： 171-178.

[14]Nigrini M J. A taxpayer compliance application of Benford[KG-*3]s law[J]. The Journal of the American Taxation Association， 1996， 18： 72-91.

[15]Rauch B， Gttsche M， Brhler G， et al. Deficit versus social statistics： empirical evisence for the effectiveness of Benfords law [J]. Applied Economics Letters， 2014， 21（3）：147-151.

[16]朱文明，王昊，陳伟. 基于Benford法则的舞弊检测方法研究[J]. 数理统计与管理， 2007（1）：41-46.

[17]刘云霞，曾五一. 关于综合利用Benford法则与其他方法评估统计数据质量的进一步研究[J]. 统计研究，2013， 30（8）：3-9.

[18]Vapnik V N， Levin E， Cunn Y L. Measuring the VC dimension of a learning machine [J]. Neural Computation， 1994， 6（5）：851-876.

[19]项前，徐兰，刘彬，等. 基于粗糙集与支持向量机的加工过程异常检测[J]. 计算机集成制造系统， 2015，21（9）：2467-2474.

[20]Pinkham R S. On the distribution of first significant digits [J]. The Annals of Mathematical Statistics， 1961， 32：1223-1230.

[21]Ciornei I，Kyriakides E. A GA-API solution for the economic dispatch of generation in power system operation [J]. IEEE Transactions on Power Systems， 2012， 27（1）：233-242.

[22]丁世飞，齐丙娟，谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报， 2011， 40（1）：2-10.

[23]杜树新，吴铁军. 用于回归估计的支持向量机方法[J]. 系统仿真学报， 2003（11）：1580-1585，1633.

[24]张丽平. 粒子群优化算法的理论及实践[D]. 杭州：浙江大学， 2005.

[25]肖晓伟，肖迪，林锦国，等. 多目标优化问题的研究概述[J]. 计算机应用研究， 2011， 28（3）：805-808，827.