层次分析法在水利工程评标过程中的应用探究

哈 仙

(新疆额尔齐斯河流域开发工程建设管理局，新疆 乌鲁木齐 830000)

水利建设工程对社会稳定和百姓生命财产安全、社会主义经济现代化发展和改革开放进程的顺利推进起着重要作用[1-2]。随着水利建设工程越来越复杂与多变等特性，评标工作在整个项目中起到的作用举足轻重，采用合理行之有效的评标办法，可以为建设单位规避风险、节约资金，评选出最优的中标单位[3-4]。

在借鉴国内外已有资料的基础上，对国内水利工程评标方法和工程实例进行了探究。金璨[5]等对单项评议法、定性或定量综合评议法、两阶段评议法等方法进行适用范围及优缺点进行分析，并对水利工程建设领域存在的串标、围标等现象提出了防治对策。吴存虎[6]等通过对现有水利工程评标体系的实施现状进行探讨，对工程量清单计价模式下的水利工程评标体系提出了意见。何芙蓉[7]分析了层次分析法的优缺点，并对区间层次分析法和模糊层次分析法进行了探究，并将层次分析法与G1法做对比，对层次分析法进行了改进。

1 基于层次分析法(AHP)计算指标权重值的原则

层次分析法(AHP)是在系统工程中将人的主观判断转化为客观评价从而对定性事件进行定量分析的一种方法，在工程评标工作中是较为理想的确定评价指标权重的方法。层次分析法可以控制主观因素的干扰，根据总目标的内在逻辑关系，将其分解为多个特征指标，再按从属关系进行聚集组合形成系统的、有序完备的阶梯层次结构。而每一层指标的相对重要程度则是根据专家的相关经验和信息通过两两比较的方式进行排序，之后计算各个指标的权重，最终形成最高层、若干中间层和最底层的结构模式，这就是层次分析结构模型。

2 计算指标权重步骤

1)基于确定的层次结构图和实际理论信息，构建判断矩阵(公式1)。判断矩阵表示各阶梯层次有关元素指标之间相对重要程度的比较。采用德尔菲标度法，对不同情况进行标度量化，得到各层次单排序权重值和基本指标层对总目标的组合权重值。

(1)

2)求出权向量，做一致性计算检验。计算通过每两个指标比较构造的判断矩阵最大特征值和特征向量，并分别对随机一致性指标RI、随机一致性比率CR以及一致性指标CI进行一致性检验。若检验满足要求，则特征向量为权向量。若检验不满足要求，则需重新构造矩阵。计算过程如下：

首先，将判断矩阵中的每一列做正规化处理，其元素一般项为，见公式(2)

(2)

然后，对判断矩阵每一行的元素进行求和计算，见公式(3)

(3)

再换算为wi，见公式(4)

(4)

求得各矩阵的向量，确定权重和排序，各要素的单层次排序为w1，w2，…，wn；w=(w1，w2，…，wn)T即为所求的特征向量的近似解。

计算判断矩阵的最大特征根，结果见公式(5)

(5)

再计算出判断矩阵的一致性指标CI，见公式(6)

(6)

构造的判断矩阵与完全一致性的偏离差随着一致性指标CI值增大而增大。当CI的值越小，则说明与完全一致性的偏离差越小。随着判断矩阵维数越多，一致性效果将越不好，引入系数RI(表1)，主要是用来消除由矩阵阶数过多影响所构造的判断矩阵不一致性。

表1 随机一致性指标RI表

而随机一致性比率CR可由公式(7)计算：

CR=CI/RI

(7)

如果求得CR<0.1，则通过一致性检验，所求得的特征向量和判断矩阵特征根是有效的，并具有良好的一致性，当CR≥0.1时，需重新将每两个指标进行比较，再构造新的矩阵。当每一个判断矩阵的一致性计算检验满足要求后，再计算各层指标对总目标的组合权重，原理过程同上。

3 工程实例

白银市某水库拦河导流工程施工项目，由于该流域内重金属污染源较集中，对该水库的水质产生巨大的危害。按照水资源污染防治条例以及地表水质要求，含重金属废水不得排入地表水体。为保证水源安全，规划建设拦河导流环保工程。将评标指标体系设立三级阶梯层次结构，包括商务、技术、资信；然后结合该工程管理的重点，对指标再进行细分。首先形成判断矩阵(表2、表3、表4、表5)，其次求出其特征向量值，并对矩阵值进行一致性计算，检验通过后求出每一个指标对应的权重值。

表2 第一层指标因素分析计算表

对第一层指标的单排序权重值进行一致性计算检验：求解λmax=3.02，一致性指标CI=0.005，由于矩阵维数为3，由此查表可得RI=0.58，一致性比率CR=0.0086<0.1，因此数据符合要求，特征向量值为：w=(0.54,0.30,0.16)。

由此可知：商务标权重值为0.54，技术标权重值为0.30，资信标权重值为0.16。

表3 第二层商务标指标因素分析计算表

对第二层指标的单排序权重值进行一致性计算检验：求解λmax=3.012，CI=0.01，查表得RI=0.58，则CR=0.018<0.1，因此数据符合要求，特征向量值为：w=(0.70,0.20,0.10)。

由此可知：商务标中的总报价权重值为0.70，分项项目单价权重值为0.20，资金流合理性权重值为0.10。

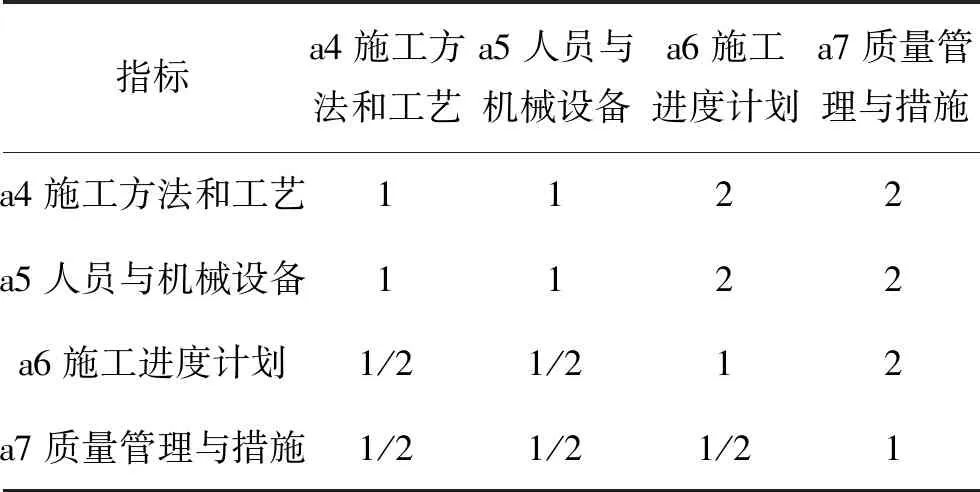
表4 第二层技术标指标因素分析计算表

对第二层指标的单排序权重值进行一致性计算检验：求解λmax=0.60，CI=0.02，查表得RI=0.90，则CR=0.022<0.1，因此数据符合要求，特征向量值为：w=(0.33,0.33,0.20,0.14)。

由此可知：技术标中施工方法和工艺权重为0.33，人员与机械设备权重为0.33，施工进度计划权重为0.20，质量管理与措施权重为0.14。

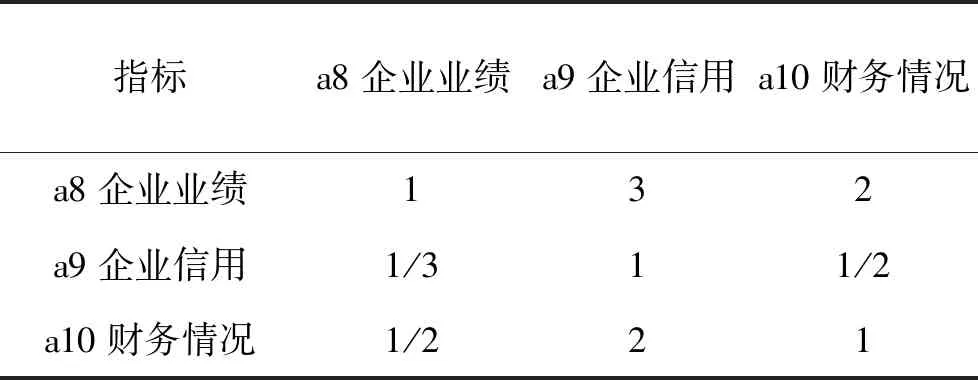
表5 第二层资信标指标因素分析计算表

对第二层指标的单排序权重值进行一致性计算检验：求解λmax=3.00，CI=0.005，查表可得RI=0.58，则CR=0.009<0.1，因此数据符合要求，特征向量值为：w=(0.53,0.16,0.31)。

由此可知：在资信标中，企业业绩所占权重值为0.53，企业信用的权重值为0.16，财务情况的权重值为0.31。

对以上数据进行计算汇总后得出各指标权重，见表6。

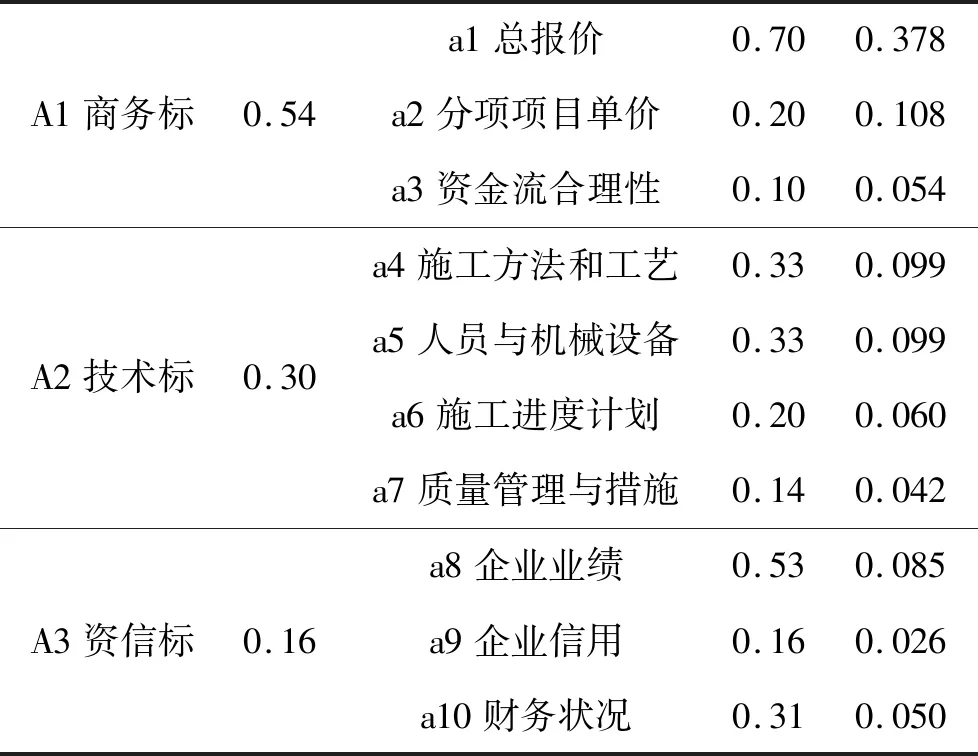
表6 综合指标权重表

4 结 语

层次分析方法对评价指标进行权重确定，具有简单明了，阶梯结构清晰等特点，能较好衡量指标相对重要性。使用时应保证所选的主要指标要素数量不漏不多，重要程度划分合理。层次分析法(AHP)属于一种决策性工具，具有系统性、适用性、简洁性等特点，但主要是针对己有初步方案的决策问题；在应用过程中，层次分析法虽然具有原理直观和清晰的特点，便于使用接受，但无论是建立构造判断矩阵还是阶梯层次结构，人的主观意识判断对结果都会产生较大影响，使得决策结果具有主观性。