基于黏弹性介质波动理论的页岩超声波数值模拟
2019-09-03徐烽淋朱洪林陈吉龙
陈 乔 徐烽淋 程 亮 刘 洪 简 旭 朱洪林 陈吉龙
1.中国科学院重庆绿色智能技术研究院 2.重庆市涪陵页岩气环保研发与技术服务中心3.中国石油川庆钻探工程公司地质勘探开发研究院 4.重庆地质矿产研究院5.“油气藏地质及开发工程”国家重点实验室·西南石油大学 6. 重庆工商大学
0 引言
页岩岩石的非均质性及层理布局的随机性,给页岩中声波传播特性研究增加了较大的难度[1-7]。因此,学者们针对超声波在层状岩石中的传播特征展开了研究。在物理实验方面,Johns等[8]用X射线衍射和扫描电镜技术得到层理是引起页岩弹性波复杂和弹性波分裂特征的重要原因;Sondergeld等[9]利用超声波透射实验的手段,分析了围压对不同层理角度页岩的纵、横波波速影响规律;Horne等[10]在建造斜井阶段利用偶极子声波测井数据来判别薄互层页岩的弹性各向异性;Domnesteanu等[11]开展了页岩的声波速度和衰减分析,结果表明页岩各向异性的大小取决于层理方向与声波传播方向的夹角以及页岩渗透率的方向;Szewczyk等[12]在一系列地震超声室内实验的基础上对曼柯斯页岩和皮埃尔页岩的弹性应力敏感度进行了研究,认为页岩分别在地震波和超声波频率下具有不同的应力敏感度。在国内,邓继新等[13]利用多频率超声波对层理发育的页岩各向异性进行了研究,给出了不同状态下,样品不同方向上声波速度、各向异性参数随压力的变化规律;王倩等[14]通过页岩的超声波实验测量探索了不同层理倾角页岩动、静态弹性模量和泊松比的关系。陈乔等[15]、熊健等[16]采用超声波透射法系统地分析了下志留统龙马溪组页岩不同层理角度的岩石纵横波速度、衰减以及频率响应,获得了层理角度与声波速度、衰减系数统计函数关系。
在数值模拟方面,Saenger等[17]利用交错有限差分法来研究孔隙度和孔洞密度与声波的响应关系,几年后,又利用旋转的交错差分网格对含黏弹性液体孔洞、无黏弹性天然气条件下的波速进行了模拟,并把模拟结果与真实测量结果进行了对比分析[18];Zhu、Baechle、Weger等[19-21]利用不同分辨率电镜X射线分辨率为3.1 μs、EPMA分辨率为1 μs、SEM分辨率为0.1 μs和铸体薄片进行数字图像分析,提取出孔隙大小、球形度、孔隙纵横波、孔隙网络的复杂程度等参数定量描述孔隙空间,在此基础上进行岩石声波数值模拟;Elhusseiny等[22]和Xu等[23]利用人工模拟方法探讨了岩石孔隙结构的超声波传播特性;Tseng等[24]利用超声物理模型测试了P—SV转换波在TI介质中的转换点及其时程的数值计算精确度,通过费曼原理和各向同性非双曲时差方程两种方法计算发现,P—SV转换波在TI介质各向同性平面传播中具有相同的转换点和时程;国内Yao等[25]利用“叠加型”多尺度随机介质模型、“区域多尺度随机介质模型”来模拟随机溶洞介质;魏建新等[26]以棍形、片形、球形、柱形、裂隙孔隙形状形态的物理模型设计了填充物相同、横向、纵向尺度不同的地震模型,在此基础上,通过数值模拟计算,分析了由孔隙结构变化引起的地震响应特征;刘向君等[27-28]基于二维声波数值模拟计算,开展裂缝模型声波衰减系数研究,同时还开展了孔洞型储层孔隙度预测模型研究。
综上所述,国内外学者主要通过超声波透射实验获得页岩声波传播规律的定性认识。同时,考虑到在物理模型实验过程中页岩岩样制备较为困难,国内学者对作为油气储集层盖层的页岩地层声波速度各向异性的岩石物理数据研究较少。仅使用实体物理模型研究复杂结构的地层声学特性是片面、非客观的,因此,认识和分析声波在复杂地层介质中的传播规律及其响应特征须结合数值模拟技术。然而,目前的数值模拟研究主要针对常规地层结构的地震识别,以页岩地层声波测井为目的的声学响应鲜有报道,相关研究将页岩当作弹性介质处理,未考虑页岩的黏弹性特征。因此,笔者基于四川盆地渝东南下志留统龙马溪组页岩岩心,建立了不同角度的层理结构模型,采用黏弹性介质波动理论和高阶交错网格有限差分方法,开展页岩超声波透射实验数值模拟研究,计算不同层理角度页岩的声学参数特征,总结页岩声波参数随层理角度的变化规律。
1 数值模拟理论基础
数值模拟中常用的波动方程可分为二阶弹性波动方程和一阶位移—应力弹性波方程组2种。由于一阶位移—应力弹性波动方程不需对弹性常数进行空间微分,利用交错网格半程计算可以避免求解时间的高阶微分,同时,网格引入的频散较小,笔者采用一阶位移—应力弹性波动方程来开展数值模拟研究。
1.1 声波波动理论
声波波动方程所包括的本构方程、运动微分方程和几何方程揭示了物体内部应变、应力和位移之间的相互关系,其中本构方程主要反映的是物体的各向异性、黏滞性和弹性等性质。Kelvin—Voigt黏弹性介质模型能较好地描述声波在介质中的衰减[29]。基于应力—应变关系、本构方程以及Kelvin—Voigt黏弹性模型,得到了二维黏弹性介质的波动方程,为了便于对其做有限差分,将二维黏弹性波动方程转化为一阶速度—应力方程,即

式中ρ表示密度,g/cm3;vx、vz分别表示速度分量,m/s;σxx、σzz、τxz、τzx分 别 表 示 应 力 分 量,MPa;λ、μ分别表示拉梅系数;λ'、μ'分别表示黏滞系数,Pa·s;Qp、Qs分别表示纵波、横波的品质因子;vp、vs分别表示纵波和横波的速度,m/s;ω表示圆频率。
1.2 数值离散
根据泰勒展开式的基本原理,速度分量vz在2阶时间精度和2n阶空间精度下的离散量为:
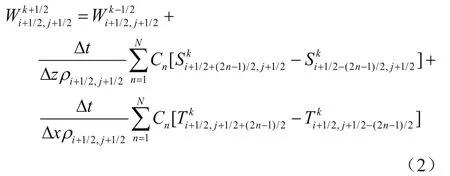
式中W表示速度分量(vz)的离散量;S、T分别表示应力分量σzz、τxz的离散量;Cn表示差分阶数;n表示空间域的阶数;Δt表示时间步长;Δx、Δz分别表示空间步长;(i,j)表示网格节点标号;k表示时间节点标号。
1.3 稳定性分析
为了避免高阶有限差分的不稳定性,需要选择合理的数值模拟参数。对于二维黏弹性介质,时间2阶和空间4阶差分的稳定性条件为[30]:
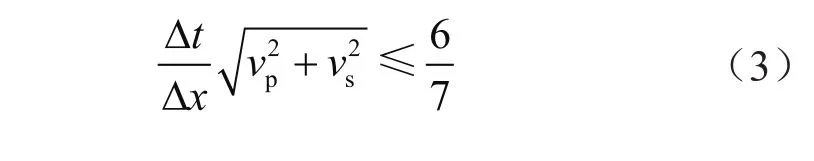
1.4 振源函数
为了更好地模拟页岩的超声波特性,振源函数是模拟页岩声波响应的关键,数值模拟中选取的声源为超声波探头原始信号为:
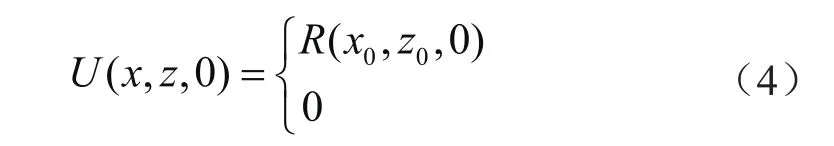
式中R表示震源函数;x0、z0分别表示坐标值。
1.5 边界条件
在数值模拟的过程中,引入完全匹配层吸收模型,在给定的模型外面构造有限厚度的吸收层,当声波传入到吸收层时能量会随传播距离呈指数衰减,从而消除边界反射对数值模拟的影响[31]。即
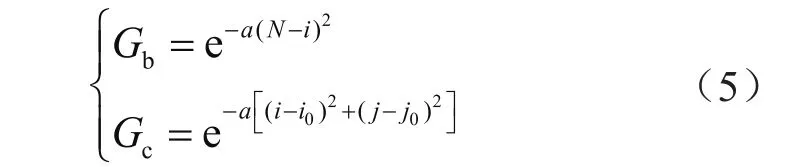
式中Gb表示边界矩形区域的表达式;Gc表示边界是个角区的函数表达式;α表示系数;N表示边界网格的层数;(i0,j0)表示4个角的内侧顶点标号。
2 数值模拟验证
2.1 模拟波形与实验波形验证
为了与物理实验相统一,针对室内标准岩心的超声波透射实验,笔者采用250 kHz的“探头频率”表示超声波频率大小。为了验证二维时域有限差分程序的正确性,计算了均匀地层条件下的声波波形,并将有限差分结果与实轴积分结果进行对比,对比结果如图1所示。图1中蓝线为有限差分计算的结果,红线表示实轴积分法的计算结果。有限差分法和实轴积分法的模拟计算结果基本一致,验证了有限差分数值模拟方法的正确性。
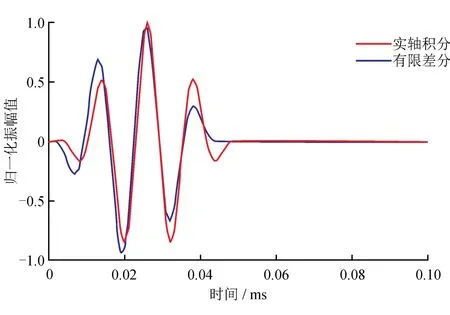
图1 二维有限差分与实轴积分波形对比图
2.2 真实岩心数值计算及验证
考虑到层理角度为页岩最显著的结构特征,因此,基于龙马溪组真实页岩岩心,建立不同层理角度的结构模型开展数值模拟(图2)。从图2可以看见,物理实验所用的真实岩心与数值模拟所用的数字岩心层理特征较为吻合,能真实反应页岩的层理特征。
岩石超声波衰减系数既可用于分析岩石的层理构造及分布,还可用于辨别岩石在地下所处的地质环境,同时,针对岩石物理状态的变化,衰减特性相较于波速特性更为敏感。衰减系数是表征衰减特性的关键参数。因此,笔者利用数值模拟不同频率下岩心的衰减系数(图3),随着测试频率的增加,超声波衰减系数呈增大趋势,数值模拟计算结果与陈乔物理实验[15]所得到总体规律较为吻合。

图2 物理实验与数值计算模型对比图
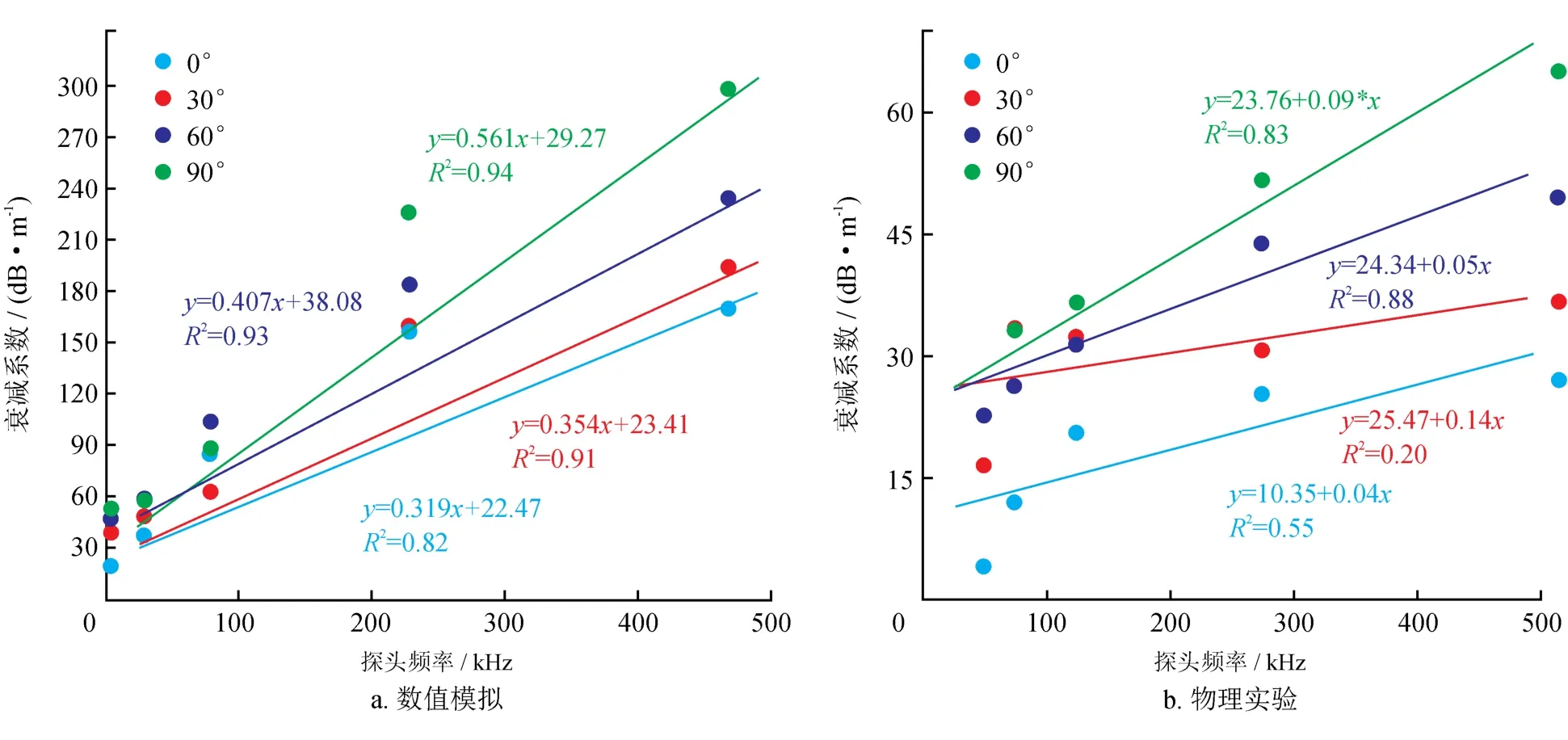
图3 超声波衰减特性结果对比图
针对岩心重复性较差的缘故,上述数值模拟计算是基于理想的岩心层理角度模型。接下来,为了进一步验证数值模拟结果的有效性,采用数值图像处理方法提取出渝东南龙马溪组真实岩心的层理角度,开展不同层理角度的衰减系数数值计算。

图4 实物岩样照片
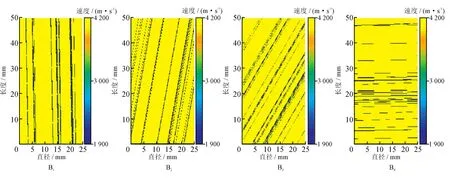
图5 实物岩样模型速度云图
图4是岩样的实物照片(记为A1~A4),从照片可以看出,页岩层理发育,层理角度在0°、45°、60°和90°变化。以图5为研究对象,利用边缘提取和Hough直线检测方法将岩心的基质骨架和层理区域进行分类识别, 基于此,建立对应的数字模型。将层理结构识别后的数字图像利用方形单元映射技术可以转化成所需的有限差分网格数据,因为数字图像是由一个个像素点排列组合而成,每个像素点都可作为有限差分计算中的四边形单元。其中,每个四边形单元所对应的节点坐标又可通过图像实际尺寸大小与像素之间的比例值,转换成所对应矢量空间的物理坐标,由此,数值图像便成功转换为正方形的差分网格。最后,依据每个像素点所对应的灰度值,为每个单元赋予相应的特征参数,从而实现将数字图像的层理结构导入数字岩心模型(图5)。从速度云图来看,B1~B4的层理倾角分别分布在0°、45°、60°和90°,与实验岩样吻合较好。最后,利用Matlab编写代码进行数值模拟计算,从图6所示的结果来看,衰减系数与层理角度都呈正相关规律变化,相同层理角度的衰减系数要小于模拟值,这是由于实物岩样(A1~A4)所对应的层理厚度略低于B1~B4,对应的衰减系数的值及上升的幅度也低于理论模型,但是从两者之间的平均值和标准差发现,数据偏离平均值程度较小,数据离散程度低,两者的衰减系数变化趋势基本一致。同时,本次实验结果与陈乔等[15]、范翔宇等[32]的室内实验结果相比较,衰减系数随着层理角度的编号趋势也基本一致,进一步说明本数值模拟方法的有效性。
综上所述,针对常规室内超声波透射法实验成本高、误差较大的局限性,笔者提出了一种模拟页岩超声波透射实验的数值计算方法,该方法与实际物理模型实验结果吻合度较高,具有进一步通过大规模数值模拟计算,开展页岩不同层理结构声学特征响应研究的价值。
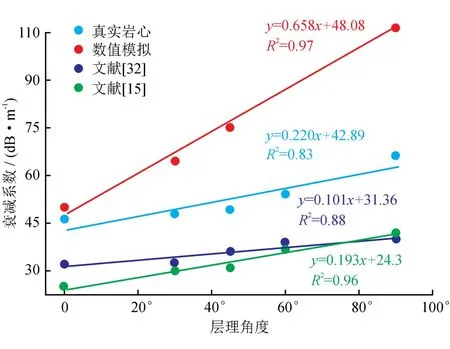
图6 室内岩样实验与数值模拟计算所得衰减系数结果对比图
3 数值计算分析
利用数值计算建立页岩不同层理角度的数字模型如图7所示。层理厚度均为0.2 mm,层理延伸方向与声波激发方向夹角分别为0°、10°、20°、30°、40°、50°、60°、70°、80°、90°(记为 C1~ C10)。
以不同层理角度的页岩数值模型为基础开展数值模拟计算,得到对应的波形,从中提取岩石声波的衰减系数和速度参数,分析层理角度对声学特性的影响。

图7 数字模型速度云图
3.1 层理角度对声波波速的影响
由图8可知,随着层理角度的增加,超声波速度呈幂函数递减规律。由数字模型速度云图(图7)可知,在层理密度相同的前提下,随着层理角度的增大,在首波传播路径上的层理界面数目越来越多,导致声波波速逐渐减小。
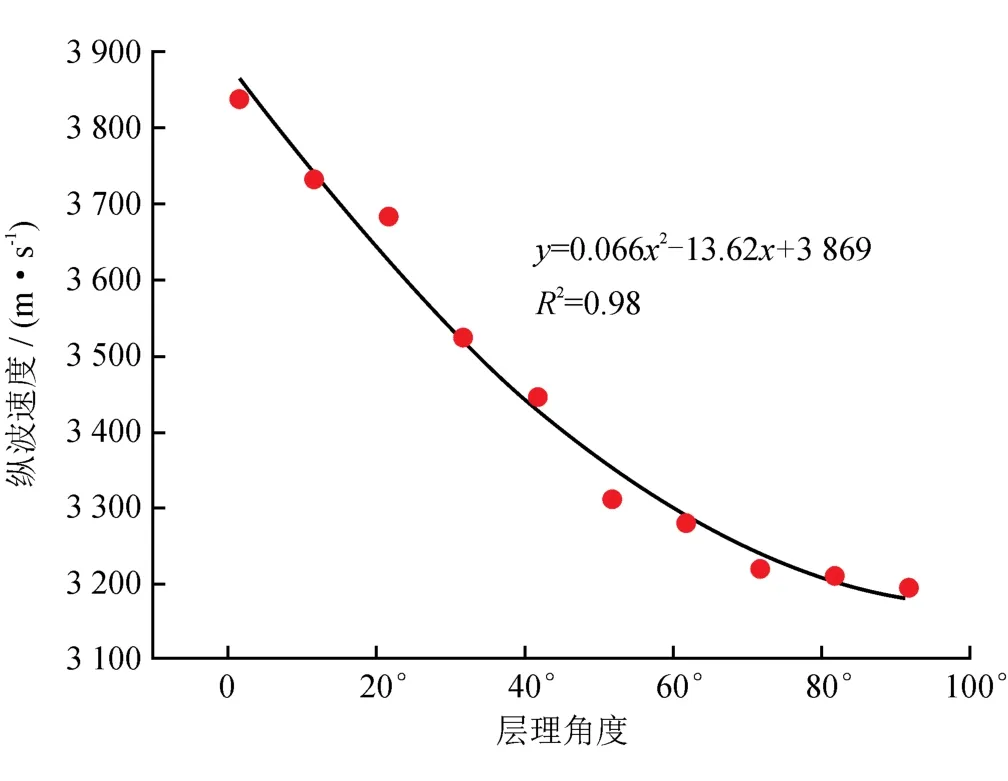
图8 层理角度对波速的影响图
3.2 层理角度对衰减系数的影响
由图9可知:随着层理角度增大,声波衰减系数呈线性递增。从数字模型速度云图(图7)可以看出:当层理角度逐渐增大时,层理在水平方向阻碍超声波在页岩中的传播路径越来越多,并且在相同尺寸岩心中,层理数目随着角度增大而增多,扩展了超声波的传播路径,导致岩石声波能量消耗增大。同时,骨架与层理面之间的界面数量也随之增多,进而产生更多的反射、散射,导致超声波穿透能量减弱,衰减系数增大。
4 结论
1)针对常规室内超声波透射法实验成本高、误差较大的现状,笔者基于黏弹性介质声波波动理论,结合高阶交错网格差分技术,建立了一种模拟页岩超声波透射实验的数值计算方法。
2)数值计算结果与物理实验得到的页岩声波特性变化趋势吻合,同时,基于理想和真实岩心的数值模拟计算的衰减特性与物理实验结果一致,表明该方法具有较强的适应性。
3)在层理尺度和密度恒定的条件下,随着层理角度的增大,波速呈幂函数递减,衰减系数呈线性增加。
4)该数值模拟方法可从微观角度分析超声波传播规律,为进一步研究分析页岩层理结构对声学特性的影响提供了思路。
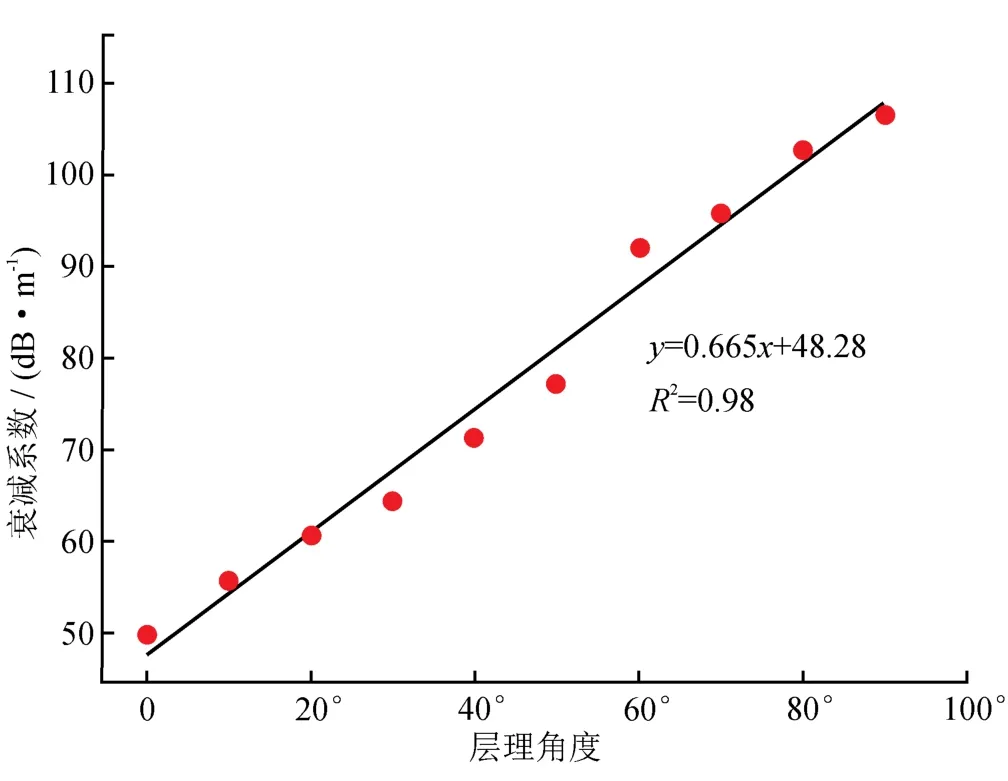
图9 层理角度与衰减系数关系图
