固井注水泥浆顶替效率评估的新模型

杨 谋 唐大千 袁中涛 张 俊 徐力群 陈 英

1.“油气藏地质及开发工程”国家重点实验室·西南石油大学 2.中国石油塔里木油田公司油气工程研究院3.中国石化西北油田分公司石油工程技术研究院

0 引言

有效驱替钻井液，提高注水泥浆顶替效率是清除钻井液窜槽、保障水泥胶结质量和水泥环密封效果的首要前提[1]。自20世纪40年代至今，注水泥浆顶替机理研究一直都是国内外固井界重点研究的课题，研究者们集中从理论和实验方面分析了顶替流体性质、流速、密度差、井眼条件、套管偏心及活动套管等对顶替效率的影响[2]。在理论方面主要应用CFD仿真和数值模型求解对固井顶替界面进行研究，CFD数值模拟以三维非定常 N-S 方程作为控制方程，采用流体体积法进行界面跟踪与重构来分析两种流体（水泥浆/钻井液、水泥浆/隔离液）顶替界面前缘和后缘位置[3-4]，分析了大位移井、大斜度井固井顶替过程为水泥浆顶替钻井液的两相流动，获得了不同井斜角和井径扩大率条件下的最低套管旋转转速[5-7]；开展了水泥浆顶替隔离液过程中，偏心度和密度差耦合条件下的顶替界面形态研究[8]。顶替理论模型包括确定钻井液滞留层厚度力学模型[9-10]、一维平板流模型及Hele-Shaw模型[11]，其中钻井液滞留层厚度力学模型未考虑水泥浆与钻井液在界面处的力学耦合关系；一维平板流模型假设两种流体在界面上无掺混，并且忽略了周向速度和径向速度；Hele-Shaw模型虽然可以通过平板流扩散方程求取界面处浓度分布来表征注顶替界面的特征，但仅适用于两相流体[12]。现有的实验方法由于模拟井筒长度以及其他条件的限制，未能真正代表实际工况。

已有的理论方法和实验方法通过简化仅开展了两相流体顶替效果分析，即在模拟过程中认为井筒被钻井液/隔离液充满，然后设置某种特定条件下的水泥浆进行顶替；而实际固井施工过程中，井筒浆柱则由钻井液、隔离液及水泥浆三相乃至更多相不同性质的流体构成，在注水泥浆前，钻井液与隔离液由于物理化学性质的差异已发生掺混，导致注入水泥浆时井筒浆柱属性、壁面和界面流体性质已发生重大改变[12]。然而，采用现有评价手段难以捕捉这些微观本质变化对注水泥浆顶替效果的影响。因此，基于已有的研究成果，借助于CFD仿真技术模拟分析不同隔离液属性条件下钻井液、隔离液及水泥浆掺混机理以及界面演变特征，可以为油气井固井施工参数优化、防止钻井液窜槽及提高固井质量奠定重要的理论分析基础。

1 物理模型建立与网格划分

1.1 物理模型

笔者建立的物理模型有关参数如下：计算区域长15 m、井眼直径为317.5 mm、套管外径为222.63 mm。为了真实地反映井筒浆体在高温高压条件下的流变属性，钻井液与水泥浆采用赫巴流变模式进行表征，其性质如表1所示。

表1 钻井液与水泥浆流性参数表

为了模拟隔离液物理性质与排量顶替界面的影响，将隔离液属性分为牛顿流体和非牛顿流体，牛顿流体考察其密度变化，在无结构力变化时对顶替效果影响；非牛顿流体研究其流变性变化对顶替效果影响，具体计算参数如表2所示。为此，研究内容包括3大类：①密度变化（case-1～case-3）；②流变性变化（case-4～case-6）；③施工排量变化（case-7～ case-9）。

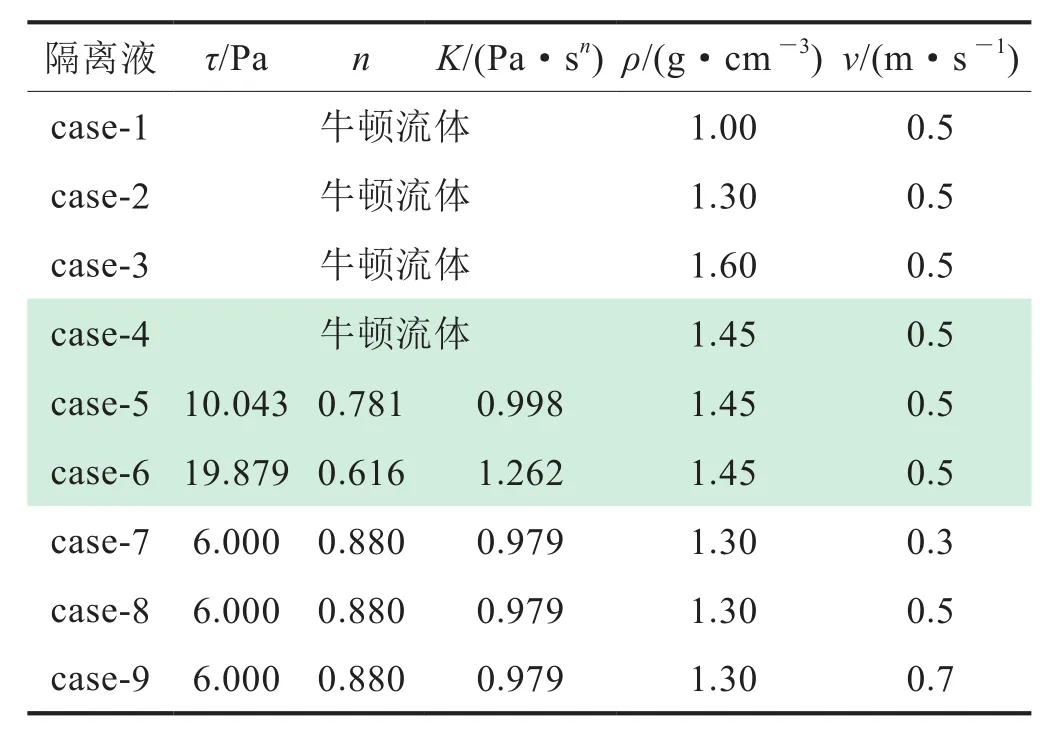
表2 隔离液参数性能表

1.2 网格划分

CFD 模拟方法是基于对多个三维非稳态偏微分方程组近似求解，为了使得仿真结果更贴近实际，需要使得网格的数目应足够大，且计算结果随着网格数增加不会出现显著变化，从而可在减少计算量的条件下提高计算稳定性和收敛速度。本模型网格划分为网格总数38 500个。在划分网格时，将井段平均划分为五段，每段长3 m，如图1所示，每一段均可独立查看其顶替情况和流体体积分数。

图1 模型与网格示意图

1.3 模型计算

本文中压力求解器采用二阶空间和一阶时间离散；求解对速度入口进行初始化残差收敛标准设置为0.001，且在每个时间步长获得收敛。多相流模型采用VOF模型，流体设置为3种相（钻井液、隔离液、水泥浆）。认为环空初始充满钻井液，流体自环空底部向顶部流动，向环空中注入一个环空体积流体所需要的时间认为一个流动周期，记作1τ。那么，流体流经一个环空小段网格耗时为0.2τ。因此，无论是注入隔离液还是水泥浆，当流体到达e)段时，a)段已经被顶替5次。选取最顶部的3 m作为观察段，通常底端井段顶替效果要优于顶端；在理论上，隔离液和水泥浆分别进入顶端的时间分别为0.8τ和1.8τ。

2 数学模型

区域内流体分布关系模型为：

式中ρ表示流体密度；φi（i=1,2,3）表示每相的体积分数，φi=0表示控制体积内无i相，φi=1表示控制体积内只包含i相；ρi（i=1,2,3）表示第i相的密度。

通过求解连续性方程可获得控制体积内i相的体积分数φi：

式中xj表示坐标方向；uj表示速度分量；t表示时间。不可压缩流体动量守恒方程为：

式中p表示压力；ui表示环空径向速度；uk表示环空轴向速度；g表示重力加速度。

环空中不同相流体间发生掺混，则用对流—扩散方程来描述：

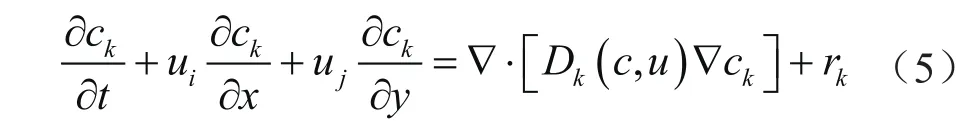
式中Dk(c,u)表示组分k的分子扩散系数；rk表示单位时间单位体积空间内因化学反应生成组分k的量，在本文中，不考虑组分化学反应生成产物，因此rk=0；ck表示组分k的质量浓度。

3 模拟结果分析

3.1 密度对顶替效果影响

从图2左侧环空体积分数曲线可发现，隔离液密度为1.0 g/cm3、1.3 g/cm3及1.6 g/cm3时，进入最顶端环空时间分别为0.53τ、0.58τ及0.68τ，如曲线图。该现象为当低密度隔离液顶替高密度钻井液时，在两界面会出现瑞利—泰勒（RT）不稳定性现象，且对界面产生的扰动会以指数形式增长，使其分散在钻井液中。因此，隔离液密度越小，在环空中窜流速度越快，分散性越好，未能形成一个整体对钻井液产生较好顶替。对比case-1至case-3中t=0.75τ的云图可发现，case-1中隔离液占据体积最大（图2云图中彩色条数字表示：0表示全部钻井液；1表示全部隔离液；2表示全部水泥浆；0～1之间就是钻井液与隔离液混合液；1～2表示隔离液和水泥浆混合，下同）。

随着顶替时间增加，从1.0τ至1.75τ时，case-1隔离液量不断增加，在水泥浆进入前（t=1.8τ），达到最大值；而case-2和case-3中隔离液分别在t=1.25τ和t=1.0τ时，环空隔离液体积分数达到最大值；表明隔离液与钻井液密度差越大，钻井液越易被顶替；因此，case-3中隔离液顶替时，其体积分数曲线上升速率最快。因为隔离液与钻井液密度差值越大，钻井液产生的浮力越大，越易被顶替；当钻井液受到的浮力小于其重力时，其易回落下沉，并在下沉过程中并聚，如case-1中1.25τ的云图。此外，从图2中可以发现，隔离液体积分数最大值均在0.94左右，小于1，表明部分钻井液滞留于壁面，导致难以清除，除非流体间发生掺混来降低钻井液在壁面的黏滞力。

图2 不同隔离液密度的顶替曲线与云图

在t=1.75τ时，case-1中无水泥浆，而case-2和case-3中水泥浆提前进入，且case-3中进入量要大于case-2（图2）。主要因为case-1中水泥浆密度比隔离液大0.6 g/cm3，对隔离液会产生较大浮力，且水泥浆黏度也较高，形成活塞效应，使得隔离液均匀被推进；当水泥浆和隔离液密度差逐渐降低时，水泥浆会快速穿透隔离液而向上流动；密度差越小，水泥浆在隔离液中产生的指进现象越严重。导致t=2.0τ时，密度差为0.3 g/cm3时（case-2），可将隔离液顶替干净；而密度差为0时（case-3），且隔离液无结构力，但壁面流体仍具有黏滞力，使得环空中间流体比壁面流体更易顶替，引起大量隔离液在壁面滞留，而水泥浆提前返出。该现象在固井实践过程中，误认为注水泥的返出已达到良好顶替效率，但实际上固井质量较差。因此，在设计隔离液性能时，若满足工况情况下，降低其密度，可起到较好隔离和冲刷井壁的效果。

为了描述case-1～case-3工况下整个井筒的顶替效果，将t=2τ时a)—e)段内滞留钻井液体积分数用柱状图来表征，如图3所示。则水泥浆体积分数可由公式（2）求得。将钻井液体积分数（φm）与水泥浆体积分数（φc）比值来表征顶替效果（）：①当时，表示顶替效果差，用红色颜色柱表征；②当 时，表示顶替效果良好，用黄色颜色柱表征；③当时，表示顶替效果优秀，用绿色颜色柱表征。

由图3中可看出，下部井段顶替效果要优于上部井段，且钻井液滞留量从底端至顶端逐渐增加；整体顶替效果case-1＞case-2＞case-3；3类工况下，在a)—c)段环空顶替效果均较好，因为越往顶端环空钻井液与隔离液混浆越严重，且流体被水泥浆顶替时间越少；在最顶端，case-1和case-2效果良好，case-1略好于case-2；而case-3效果差。表明在顶替过程中，隔离液密度可设计较低，不仅可扰动钻井液，还可在水泥浆中产生较大浮力，实现良好顶替效果；当隔离液密度与水泥浆密度差较小时，扰动力和浮力效用降低，导致驱替效果降低。在实际工况下，要求设计的隔离液密度要小于水泥浆，可以避免水泥浆在隔离液中窜槽。

图3 不同隔离液密度的环空各段滞留情况图

3.2 流变性对顶替效果影响

为了模拟隔离液流变性变化对顶替效果的影响，取其密度为钻井液与水泥浆的平均值，流变性分别为牛顿流体、与钻井液相似、与水泥浆相似的3种工况，其模拟结果如图4所示。由图4可看出，t介于0.75τ～1.00τ，随着隔离液黏度增加，3种条件下环空隔离液量也逐渐减小，其中case-4隔离液占据环空更为迅速，斜率更陡峭，即驱替钻井液效果更好；在t介于1.00τ～1.75τ流动阶段，case-4中逐渐增加；结合t=1.25τ的云图可看出：隔离液无结构力时，对环空冲洗效果要好于拥有结构力的隔离液体系。同时，当水泥浆与隔离液间为正密度差时，顶替过程中，随着隔离液黏度增加，指进现象逐渐降低，如图4中case-4～case-6中t=1.75τ时所示。当隔离液无结构力时，随着隔离液密度增加，环空中滞留隔离液量增大，如图2中case-2～case-4中t=1.75τ时所示。当注水泥浆结束时，t=2.00τ时，case-4中环空水泥浆体积分数要多于case-5和case-6。因此，在顶替过程中，若设计密度为：钻井液＜隔离液＜水泥浆，为了提高顶替效率，尽量设计低黏度隔离液体系。

图5是case-4～case-6环空钻井液滞留柱状图。从滞留图中可以看出，对于整段井筒来说，隔离液黏度较低时，其顶替效果要优于黏度较高时。但在钻井液、隔离液与水泥浆形成一定密度差条件下，这时改变隔离液流变性对顶替效果影响不大。结合图5中case-5和case-6柱状图a)和b)段结果表明，若增大隔离液用量，则也会达到良好的顶替效果。

3.3 注入速度对顶替效率的影响

从case-1～case-3中研究发现，降低隔离液密度有助于提高顶替效率，为了维持井壁稳定和溢流发生，通常隔离液密度最小密度与钻井液相近。为了模拟隔离液注入排量对顶替效果影响，设计隔离液密度与钻井液相等，其流变性为隔离液与钻井液间的中间值，模拟中三种流体均为赫巴流体，如图6中case-7～case-9所示。随着流速增加，环空中隔离液体积分数逐渐增大，钻井液滞留量逐渐减少；当流速为0.7 m/s时，t=1.25τ时，环空中几乎无滞留钻井液，达到最佳顶替效果。隔离液流速越大，使其产生的径向和周向速度较大，该速度作用力可较好的清除井壁/套管壁残余钻井液。同时，对比case-2和case-8可以发现，隔离液在相同密度条件下，其流变性越好，即结构力较弱的情况下，对井筒冲洗效果越好，进而获得更好的顶替效果。

图7为上述3种工况下钻井液滞留柱状图，从图中可看出，全井段顶替效果为case-9＞case-8＞case-7。同时，当流速为0.3 m/s和0.5 m/s时，两者顶替效果较为近似，结果表明：当隔离液流变性为钻井液与水泥浆中间值时，一定范围内的流速对顶替效果影响不大；只有流速增加到某个临界值时，顶替效果才会有较大改善。

4 顶替效率模型拟合

将上述数值模拟数据，进行拟合，可获得在环空水泥浆分数与三相流体密度结构、黏度结构、流变参数及流速的关系模型，以便应用，如式（6）所示：

式中φc表示水泥浆体积分数；ρc、ρs、ρm分别表示水泥浆密度、隔离液密度与钻井液密度；μc、μs、μm分别表示水泥浆黏度、隔离液黏度与钻井液黏度，非牛顿流体采用其表观黏度；v表示流动速率；λ、α、β、χ、δ、ε表示常数参数。

图4 不同隔离液流变性的顶替曲线与云图

图5 不同隔离液流变性的环空各段滞留情况图

图6 不同施工排量的顶替曲线与云图

图7 不同施工排量的环空各段滞留情况图

表3 拟合方程参数表

根据case-1～case-9数据，计算最终得到数据如表3所示。最终顶替效果计算表达式为式（7）：

为了验证拟合数据的有效性，应用CFD模拟数据和拟合模型进行校核分析，选用参数为v=0.3 m/s，ρm=1.10 g/cm3，ρs=1.20 g/cm3，ρc=1.30 g/cm3，μm=0.259 Pa·s，μs=0.255 Pa·s，μc=0.399 Pa·s。模拟数据和拟合数据分别为0.922 6和0.889 3，相对误差为4.6%，表明拟合模型具有一定的参考价值。但该模型依托特定物理模型条件下拟合结果，可能具有一定差异性，但该方法仍可为顶替效率预测提供参考。

5 结论

1）隔离液密度低于钻井液或与其相近时，在顶替钻井液初期会产生较为严重的混浆，但该混浆有利于降低壁面钻井液黏滞力，清除滞留钻井液，进而在高密度水泥浆作用下有利于提高顶替效率。

2）高密度，低黏度隔离液虽能快速清洗井筒钻井液，但其黏度低于水泥浆，易产生指进现象，导致水泥浆提前返出井口，误为顶替效率较好。

3）隔离液密度位于钻井液和水泥浆之间时，低黏度隔离液不仅有助于清除壁面钻井液；而且有利于被水泥浆顶替。

4）隔离液排量低于临界值时，排量对顶替效果影响不大；当高于临界值时，顶替效果改善较显著。

5）基于CFD模拟数据建立的顶替效率模型，与模拟结果吻合度高，具有推广价值。