车辐式索桁架模态分析与试验研究

王泽强，刘占省，韩庆华，张维廉，周黎光

(1.天津大学 建筑工程学院，天津 300072；2. 北京市建筑工程研究院有限责任公司，北京 100039；3. 北京工业大学 建筑工程学院，北京 100124)

车辐式索桁架是一种受力高效、结构轻盈的典型预应力钢结构体系，主要由柔性的拉索和刚性的撑杆组成。在动力荷载作用下，这种柔性结构会发生拉索松弛和拉索预应力损失、撑杆轴力方向改变、甚至发生结构系统性共振等危害。在对结构进行抗震、抗风、冲击荷载和爆炸荷载的研究中发现，结构的动力响应不仅与外界的激励和随时间的变化规律有关，更取决于结构自身的动力特性，即结构的振型和振动频率。因此，在结构的动力响应分析之前，有必要对结构进行模态分析研究。

学者们对大跨空间结构的静力性能、模型试验研究较多，对车辐式索桁架结构的模态分析较少。蔺军等[1]对3种葵花型空间索系结构模态对比分析，研究不同预应力水平对结构的自振特性影响规律。郭彦林等[2]对宝安体育场进行缩尺模型试验，分别对主体索系结构和整体索膜结构的模态进行对比分析，研究表明，膜材预应力对模态的影响不明显。孙文波等[3]选取佛山世纪莲体育中心的车辐式索膜结构为研究对象，着重分析不同预应力度和不同膜的张拉刚度对结构自振特性的影响。结构的模态实验方面，李峰等[4]针对凯威特-联方型弦支穹顶结构模型进行模态分析，探讨了外部荷载、矢跨比、环数比及支座形式等参数对结构自振特性的影响。Chen等[5]提出了一种高效的对称方法来确定多种独立自应力模式下各种索杆结构的整体预应力模态。对于独立单层外环梁、双层柔性拉索、小直径内环的车辐式屋盖体系，结构的动力特性尚有待探究。

本文首先介绍了车辐式索桁架结构模态试验模型的设计方法，通过ANSYS 建立结构的有限元模型进行模态分析，通过试验测得结构的自振频率和相关振型，与理论结果对比分析，验证计算机模拟的可靠性。通过研究结构成型态初始预应力水平、矢跨比和内外环直径比对结构模态的影响和变化规律，为类似结构设计和动力性能评估提供参考。

1 试验模型设计

1.1 相似比关系

试验以60 m直径的某圆形车辐式索桁架结构工程为背景，几何缩尺比例为1∶10，应力比为1∶1。长度和弹性模量的相似系数是设计时首先确定的条件，针对本试验几何相似系数Sl=1/10，模型采用与原结构模型相同的材料，故材料相似系数Se=1/1。从而，模型与原结构模型中拉索、撑杆的截面积比为1∶100。为满足应力比1∶1的要求，需要进行结构质量补偿，计算出9倍的补偿自重荷载所产生的等效节点力，在节点施加质量块补偿荷载。文章主要考虑满足结构缩尺前后应力相等的要求。柔性结构缩尺前后刚度的变化主要受位形和索力影响，质量块以节点荷载的形式作为质量补偿，试验结构的理论质量减少。得到的试验频率虽与原始模型有误差，但与试验理论模拟一致，验证了有限元模拟的可靠性。

在计算分析结构模型、结构设计图纸前提下，选择结构模型试验的各种杆件。其中，模型用的索材选用钢丝绳，弹性模量为1.3×105MPa，准确值由材料试验确定；钢管选用Q235B钢材。结合市场供应情况，模型选用的材料和规格见表1。

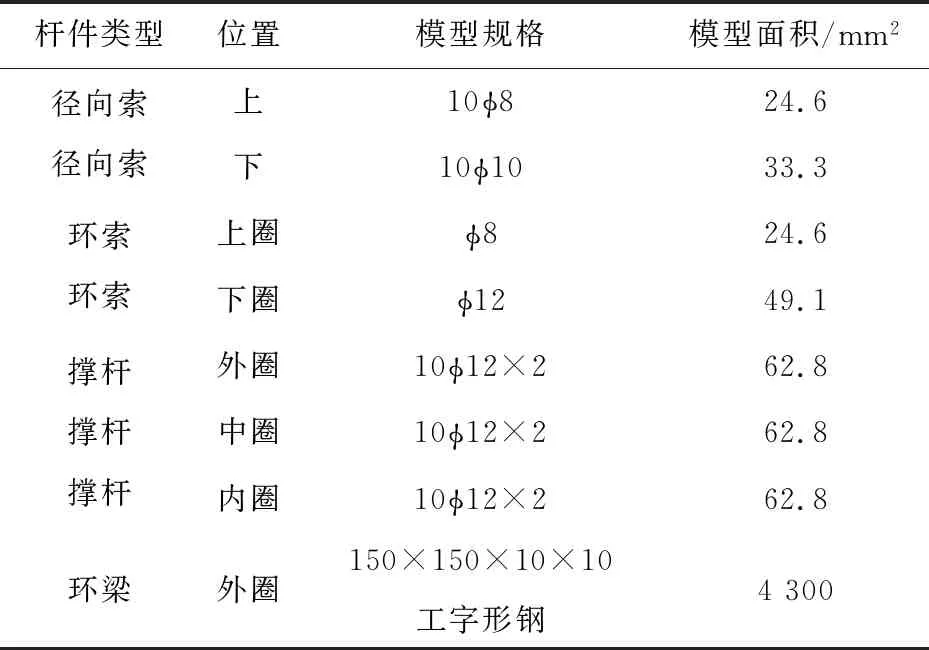
表1 模型选用的材料和规格Table 1 Model selection of materials and specifications

1.2 结构模型与节点设计

结构模型直径为6 m，由10榀鱼腹式索桁架、2道柔性环索和1道刚性受压环形工字梁组成。整体结构属于自平衡结构体系，即屋盖对主体结构只传递重力作用，无弯矩作用。屋盖结构下方有8根圆钢管柱支撑，每根柱下通过4根地锚螺栓固定。模型三维图及立面图如图1～图3所示。

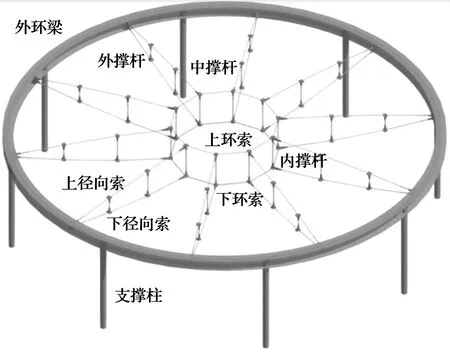
图1 三维图

图2 立面图

图3 实际结构模型

径向索与撑杆、环向索与撑杆等连接节点的形式与构造以实际工程设计图纸为依据，最终确定出既可以用于模型试验，又具有可实施性的合理节点形式，并且遵循力学模型相似原则。具体节点设计如图4～图6所示。

2 有限元模态分析

模态分析采用假定的计算模型，跨度为6 m，矢高为200 mm，内环直径为1 500 mm。利用ANSYS软件中APDL语言建立模型，撑杆杆件采用link8单元，弹性模量为2.06×1011N/m2，屈服强度为235 N/mm2；拉索采用link10单元，弹性模量为1.3×1011N/m2，以施加初始应变的方法施加预应力；环梁采用beam188单元；活荷载为500 N/m2。

图4 内撑杆下节点

图5 内撑杆上节点

图6 中、外撑杆上、下节点形式

有限元软件ANSYS中提供了多种相应的求解方法，主要有Subspace(子空间法)、Lanczos(分块兰克索斯法)、Reduced(凝聚法)、Unsymmetric(非对称法)、Damped(阻尼法)和QR Damping(QR阻尼法)。对预应力钢结构而言，高阶振型参与比重变大，仅求解低阶阵型对整个结构的分析并不充足。这就对结构特征值和特征向量的计算提出了更高要求，需更高效的大型稀疏对称矩阵广义特征值求解算法。因此，借助ANSYS软件用Lanczos法，对车辐式索桁架屋盖结构缩尺模型的模态进行分析，提取前6阶阵型和频率，振型如图7所示，频率见表2。

由图7可知，前30阶模态振型中：第1、2阶为内环呈反对称形式上下振动；第3阶为内环扭转振动；第4阶为内环相对扭转振动；第5、6阶均为索桁架呈对称上下振型，第7阶为内环上下振动；第8、9阶为索桁架水平面对称摆动振动；第10、11阶为索桁架水平面反对称摆动；第12阶至第21阶皆为索桁架水平方向摆动振动；第22阶至第30阶皆为索桁架平面外扭转振动。

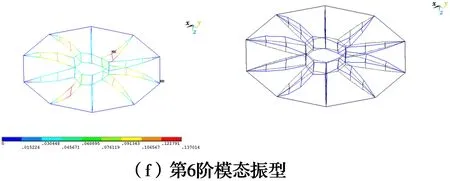
图7 前6阶模态振型Fig.7 6 steps mode shapes of experimental

综上，振型特征可以概括为：低阶振型以竖向振型、水平竖向混合振型为主，高阶振型以水平振型为主；随着频率增加，水平振型开始出现，说明结构整体的竖向刚度要弱于水平侧向刚度，这是由于车辐式索桁架结构中各榀索桁架单元与外环梁铰接于一点连接，导致竖向刚度不足，因此，提高预应力水平或设计成双层外环梁有利于提高结构的竖向刚度。由表2中可知，结构中心对称会导致多阶频率相等的情况发生；随着结构阵型阶数的增高，自振频率越来越大；结构自振频率密集，且前若干阶自振频率均偏低，试验结构的基频在5 Hz左右，说明结构的整体刚性较好。

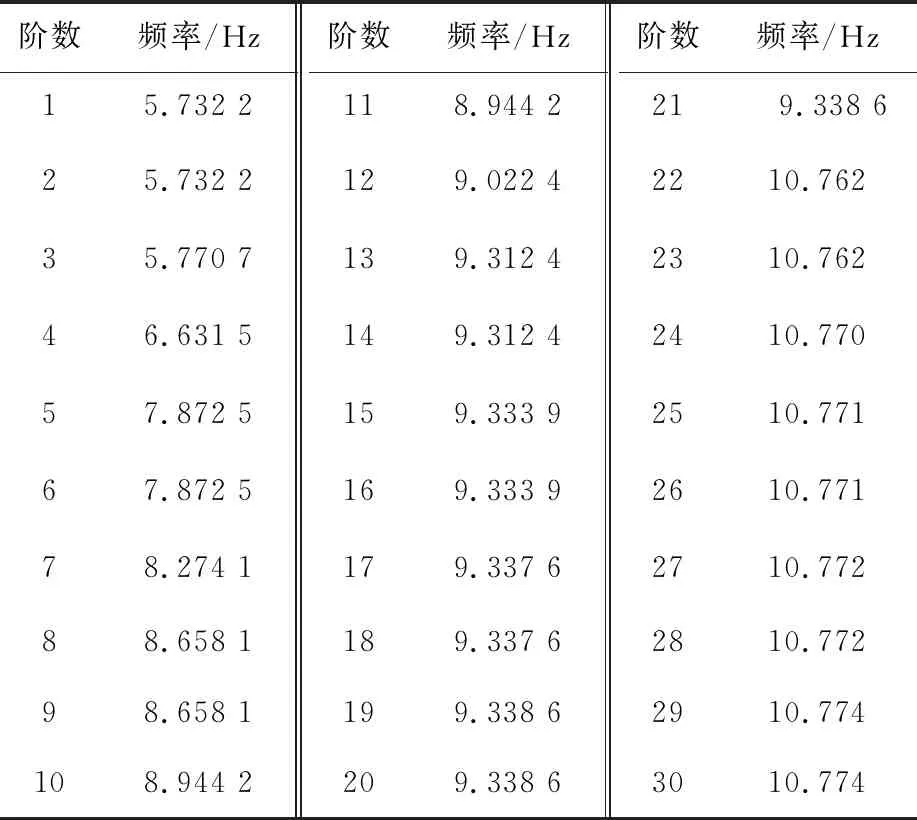
表2 模型结构前30阶自振频率Table 2 30 steps mode frequencies of experimental model

3 试验模态分析

3.1 试验设备

试验对象为车辐式索桁架屋盖结构的成型态，采用正弦激振法测量结构的动力特性。实验仪器如图8所示：DF1010超低频信号发生器，用以产生正弦波；KD5701功率放大器，将信号放大；电磁激振器，固定于激振点处，与模型连接以施加正弦激振力；加速度传感器，利用热熔胶水平或竖直粘结固定于节点上；动态信号采集仪器，对结构加速度进行监测，包括16通道模块1个。

由于采集通道数量的限制，加速度传感器布置在结构上层节点处，共布置16个加速度传感器。对称的第1榀和第6榀布置，其相邻榀和间隔榀分别布置，最大限度的保证加速度传感器的均匀布置。加速度测点布置如图9所示。

图9 测点布置

3.2 试验方案

将激振器的顶杆与结构通过钢丝和热熔胶固定，以带动结构产生反复的振动。首先，激振点选择第1榀内撑杆下节点，激振器沿内环索垂直方向竖向激振。将实验仪器安装调试好，加速度传感器竖向固定，以测得第1、2阶振型对应的频率。设置低通滤波器为10 Hz，过滤掉高阶频率的干扰。手动调节信号发生器以改变不同的频率，此为扫频过程。观察各点加速度时程曲线，当在一定频率范围内，各点加速度时程曲线的相位同时出现峰值，此时继续调节信号发生器的频率，振幅最大的加速度时程曲线对应的为第1阶振型，取其振动周期的倒数为结构的第1阶自振频率。由于结构对称，将加速度传感器布置旋转90度，测得第2阶自振频率。按照此方法继续调节信号发生器，查找下一阶竖向振型对应的自振频率。

将加速度传感器水平方向放置，选择一内撑杆下节点作为激振点，激振器水平激振，用同样的方法测得水平振型对应的频率。实验设备连接示意图如图10所示。

图10 实验设备连接示意图Fig.10 Laboratory equipment connection diagram

3.3 实验结果及分析

激出结构高阶频率需要激振器具有较大的激振力，才能使加速度时程曲线更明显，由于电磁激振器的限制，实验只测得结构前4阶频率。对试验所得到的结构模型加速度时程曲线进行分析。第1次共振：加速度传感器竖向放置，信号发生器产生的正弦激励信号的频率为5.51 Hz，加速度时程曲线振动周期为T1=0.184 s，则第1阶频率f1= 5.412 Hz；后续分析方法与之一致。试验模型自振频率试验值与理论值对比见表3。

表3 模型自振频率试验值与模拟值比较Table 3 Comparison between test and simulation results of nature frequencies

实验发现结构自振频率试验值整体偏小，误差原因可能是结构成型态拉索预应力并未达到设计值。 误差总体在10%以内，表明试验值与理论值吻合较好。

4 参数分析

4.1 拉索预应力的影响

车辐式索桁架屋盖结构中预应力水平是指拉索的预应力大小，是表征预应力钢结构结构刚度的重要指标。文中将试验张拉索定义为预应力水平的100%。在各构件预应力值的基础上，将结构的上径向索、下径向索、上环索和下环索的预应力值同时放大或缩小0.6倍、0.8倍、1.2倍和1.4倍，表4给出了结构成形态在不同预应力水平下，各主要构件的内力。陈志华等[6]通过对天津保税区商务中心弦支穹顶结构的外环索预应力调整进行模态研究，表明结构预应力度对自振频率影响并不显著。刘婷婷[7]研究弦支网壳与单层网壳自振特性对比，振型与相应的单层网壳有本质的区别，但预应力大小对结构频率影响并不显著，这是因为弦支网壳刚度和质量的主要来源为上层刚性网壳。对于全柔性的预应力索结构，孙文波等[3]研究佛山世纪莲车辐式索桁架，发现预应力度与结构前几阶自振频率的关系基本呈线性变化，影响较大。蔺军等[1]对葵花型索桁架研究发现预应力水平直接影响着结构的频率，这是因为全柔性结构的刚度完全由预应力提供。

表4 不同预应力水平成型态各类拉索的内力值Table 4 Force of Structure in different prestress

图11给出了不同拉索预应力水平结构成型态下，前60阶振型的自振频率。首先，前几阶振型中，不同拉索预应力水平的结构没有发生变化。但随着预应力水平的增加，结构振型相对应的频率也在增加，如对应的基频分别为4.440 2、5.127 1、5.732 2、6.279 3、6.782 3 h；由图11可知，高阶频率比低阶频率变化显著，表明增加预应力水平，提高水平刚度比竖向刚度更明显。因此，适当提高结构的预应力水平，可提高结构的抗变形能力。

图11 不同预应力水平成型态前60阶振型频率Fig.11 frequencies of Structure in different

4.2 矢高的影响

矢高是指结构支座至结构最顶部的竖向距离。在预应力索网结构中，相同荷载的作用下，矢高的增加有利于提高结构的整体刚度、抵抗竖向位移的能力。薛素铎等[8]通过研究劲性支撑索穹顶，得出矢高增加不利于结构扭转刚度的结论。

为尽可能减少设计参数的改动、保持撑杆与下径向索角度不变，本结构通过改变撑杆的长度，以达到改变结构矢高的目的，如图12所示，f表示矢高高度，Δf表示矢高增量。根据《索结构技术规程》 3.2.9规定，对于双层索系玻璃幕墙，索桁架矢高宜取结构跨度的1/10 ～ 1/20。该试验矢高采取150、200、300、400、500、600 mm，不同矢跨比下节点位移如图13所示。内撑杆、中撑杆、外撑杆的高度原始比例保持一致，为1∶1.67∶1.99。表5给出了不同矢跨比成型态撑杆长度。

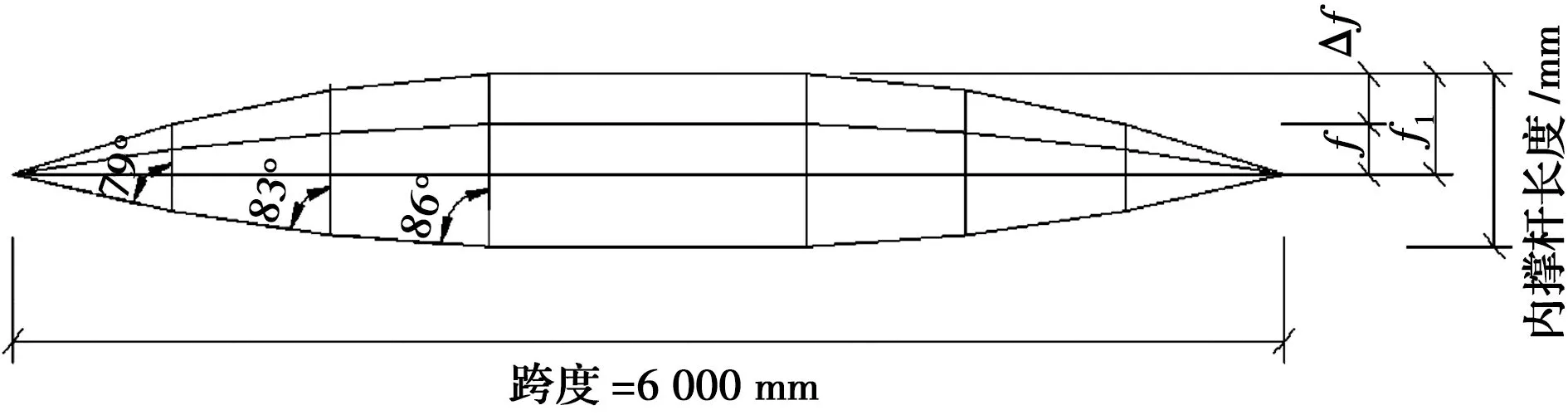
图12 结构立面图

图13 不同矢跨比下节点位移云图Fig.13 Node displacement cloud graph in different

矢高/mm矢跨比内撑杆长度/mm中撑杆长度/mm外撑杆长度/mm1501∶404393682212001∶304894082463001∶205894942964001∶156895783465001∶127396203716001∶10789662396

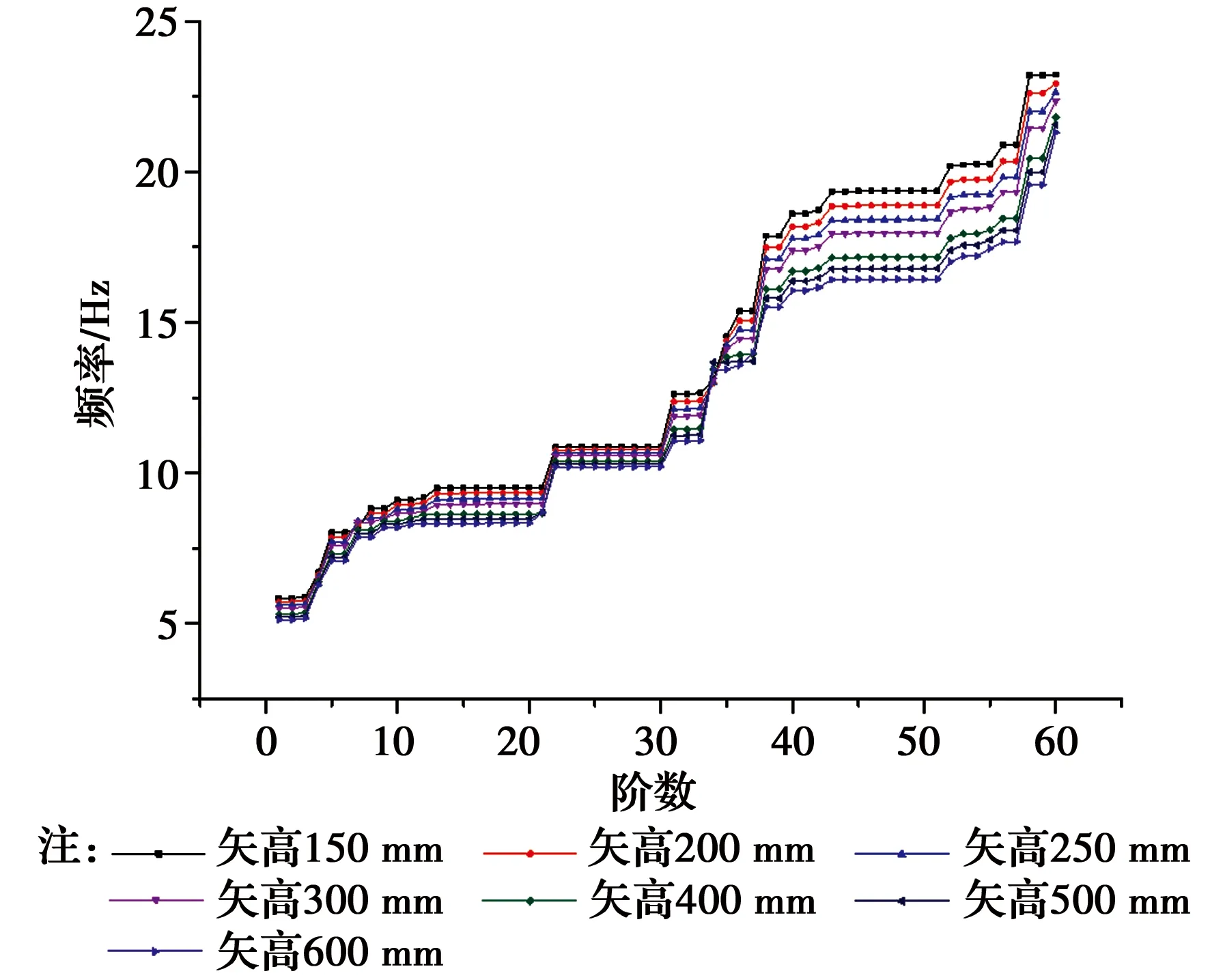
图14 不同矢跨比成型态前60阶振型频率图Fig.14 Frequencies of structure in different span-to-rise

图14给出了不同矢高结构成型态下前60阶振型的自振频率。随着矢高增大，低阶自振频率略有减小，但不显著，高阶自振频率减少比较明显。说明矢高增加，结构水平刚度降低，对结构抗扭不利。

4.3 内外环直径比的影响

最早一批双层车辐式索桁架结构用于体育馆等封闭屋盖建筑，如北京工人体育馆、四川广汉文体馆、布鲁塞尔世博会美国馆等，此类体育馆特点是内环为刚性结构且直径较小。近年来，大型车辐式索桁架结构体育场中，内环不封盖、开口大，为柔性拉索。郭颜林等[9]参考北京工人体育馆为例，研究柔性内环替代刚性内环的可行性，得出柔性内环的用钢量仅为刚性内环的33%。但实际工程中，柔性内环索下料长度误差较大，对结构影响较大。

图15 不同内外环直径比节点位移云图Fig.15 Node displacement cloud graph in different

针对车辐式索桁架结构，柔性内环直径大小对其力学性能的影响和变化规律研究较少。根据《索结构技术规程》的规定，对双层索系屋盖，当平面投影为圆形式，中心受拉与结构外环直径比宜取1∶5～1∶12。深圳宝安体育场、广州佛山世纪莲体育场内环与外环比约为1∶2。在保持矢跨比、环向等分数不变的情况下，选取内外环直径比为1∶2、1∶4、1∶6 三种工况。不同内外环直径比节点位移云图如图15所示，结构尺寸见表6。

表6 不同内外环直径比的结构尺寸Table 6 Different ring cable diameters of structure

图16 不同内外环直径比成型态前60阶振型频率图Fig.16 Frequencies of structure in different

图16给出了不同内外环直径比结构成型态下，前60阶振型的自振频率。1∶2内外环直径比的振型已发生变化。第1阶为内环扭转振动；第2、3阶则为内环呈反对称形式上下振动，与文献[2]一致，说明了分析模型的准确性(如图17所示)。

随着内环直径的减小，结构的第1阶振型由扭转振动变为竖向振动，表明内环直径大的扭转刚度弱于竖向刚度，内环直径的减小相对提高了结构的水平扭转刚度。高阶振型以水平振型为主，高阶频率的增大也说明了上述结论的正确性。

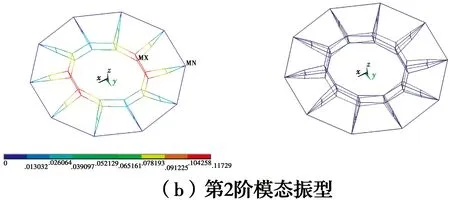
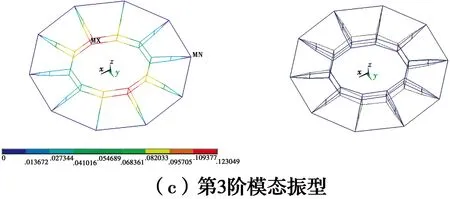
图17 1∶2内外环直径比前3阶模态振型Fig.17 3 steps mode shapes with 3 meters

5 结论

从理论和试验两方面研究了某圆形车辐式索桁架结构1∶10缩尺模型的模态特性，得出成型态阶段的模态参数。利用ANSYS有限元软件进行建模计算分析；采用正弦激振法测试动力特性，与理论值对比分析，明确了结构模型的自振特性；对预应力水平、矢高和内外环直径比等参数进行研究，为结构设计提供了相关参考，得出如下结论：

1)前4阶振型的频率均在10 Hz以内，表明结构为低频动力响应，验证了车辐式索桁架结构自振频率较小且分布密集的结论。结构本身有多条对称轴，故有部分频率相等，振型大多为正对称或反对称形状。

2)车辐式索桁架的结构刚度由预应力提供，结构预应力水平越大，结构的刚度越大，则振型频率越大。适当提高结构的预应力水平有利于结构整体的抗风性能和抗变形能力。

3)该结构频率随矢高增加而减小，高阶频率更为明显；内外环直径比对结构振型影响显著，内环直径增大，结构扭转刚度相对减弱。故在初步设计阶段，不能忽略矢高、内外环直径比对结构动力性能的影响。