全长粘结锚杆锚-浆界面应力的分布规律

宋洋，王贺平，许怀玉，张维东

(辽宁工程技术大学 a.建筑与交通学院；b.土木工程学院，辽宁 阜新 123000)

在隧道、基坑等锚杆支护工程中，主要有两种锚杆类型：一是部分粘结式锚杆，二是全长粘结式锚杆；相比之下，全长粘结式锚杆具有以下优点[1]：全长粘结锚杆提高了破碎岩体的粘聚力和内摩擦角，形成了支护共同体，加强了锚固范围内岩层整体性；在一致的工况下，全长粘结锚固式锚杆的强度储存能力是部分粘结锚杆的数倍，抗剪切破坏能力也优于部分粘结型锚杆，增强了锚杆系统的作用效果；全长粘结式锚杆锚固范围大，锚固范围内每一点都具有支护力，增强了锚固效果。注浆锚杆的破坏形式[2]一般分为4种:1)锚杆破断；2)锚杆与灌浆体界面破坏；3)注浆体与岩土体界面破坏；4)复合破坏。每种锚固破坏形式和机理都具有不同的影响因素。Hariyadi等[3]对静态拉拔荷载作用下锚杆的失效机理和强度进行了研究。Zhou等[4]在中性点理论基础上，建立了在地震荷载作用下完全灌浆锚杆与围岩的联合作用力学模型。针对锚杆多屈服破坏条件，提出了一种新的全注浆锚杆数值模拟方法。Kim等[5]、Tremblay等[6]、Chalie[7]在荷载传递理论的基础上，分析得到杆体与注浆体的粘结力在最初的力传导期间发挥主要作用，当粘结力被克服时，杆体与注浆体之间产生相对位移，发生剪切滑移破坏，界面之间的摩擦阻力占主导作用。利用客观可测物理量与数值模拟技术相结合进行分析研究，可以获得模型内部状态全局的变形破坏过程。McVay等[8]通过有限元模拟技术对粘结型锚杆在拉拔工况下进行模拟，得到了与实验结果具有高度一致性的结果。模拟结果表明，锚-浆界面先发生破坏，随着荷载增加，基体表面形成隆起，不断膨胀增大直到锚固系统破坏。并没有构建全长粘结型锚杆锚-浆界面破坏应力-应变相互关系模型。

目前，在工程中经常通过经验与理论公式相结合的方式进行锚杆设计施工。对于锚杆与注浆体之间的应力传导分布、锚固机理研究还有很多有待完善的地方。本文通过建立锚杆与注浆体相互作用关系模型，结合数值模拟技术，研究拉拔荷载下对全长注浆粘结型锚杆的锚-浆破坏类型,基于局部变形理论,进行了锚固机理的研究与分析。

1 力学模型的建立

当拉拔荷载作用在较高强度的锚杆上时，若注浆体与岩石界面的相对粘结度高于锚杆与注浆体界面，此时，锚固系统先于锚杆与注浆体界面产生破坏。根据局部理论[9]，采纳文献[10]力学模型的建立与公式推导，并将公式中r的定义由锚固体半径改为锚杆半径。将岩体与注浆体看成相对变形量为零的整体，称为稳定体。假定稳定体与锚杆的相互剪切作用产生了线性的相对滑移，其力学计算简图如图1所示。

则距离锚头位置为x处的剪力集度[9]为

q=-ksv(x)

(1)

式中：v(x)为x点处的微段锚杆与稳定体的相对剪切位移；q为单位长度锚杆上的剪力集度，kN/mm；ks为综合切向刚度系数，GPa，同时

q=2πrτ(x)

(2)

式中：r为锚杆的半径:τ(x)为距离锚头x位置处锚杆和稳定体界面上的剪应力。联立式(1)、式(2)可得

(3)

相对位移v(x)在与距o点x处锚杆的轴向应变的关系式为式(4)。

(4)

式中：ε(x)为距离锚头为x位置处锚杆的轴向应变；A1为锚杆的横截面积；E1为锚杆的弹性模量。

根据锚杆微段的受力平衡可得

dF(x)=-2πrτ(x)dx

(5)

由式(5)可得

(6)

联立式(3)、式(6)，可得

(7)

式(4)、(7)联立，移项，对其二次求导，可得

(8)

εx-α2εx=0

(9)

解得

εx=c1eαx+c2e-αx

(10)

将边界条件带入

(11)

当x=1时：εx=0

(12)

将式(11)、式(12)带入式(10)，得

将c1、c2带入式(10)，得

(13)

将应变公式带入式(13)，可得

(14)

(15)

(16)

2 数值实验

2.1 算例验证

假定k1=1.0 GPa，锚杆半径r=10 mm，锚杆弹性模量E1=210 GPa，锚杆长度1.5 m，F0=180 kN。经计算α=3.8。

为了深入研究锚杆基于锚-浆破坏的锚固机理，对锚杆在拉拔工况下进行数值模拟，分析在拉拔力作用下锚杆与注浆体界面的受力情况。

2.2 数值模拟

2.2.1 计算假定 采用有限元软件Flac 3D进行数值模拟。依据上文算例，采用了以下假定：

模型岩体为均质、连续、各项同性体，模型锚杆采用实体单元建立，视为弹性体材料。

假设注浆体与围岩不发生剪切破坏，视为整体，保证在拉拔工况下锚杆与注浆体发生相对位移。

为了更好地模拟拉拔工况下锚杆与注浆体界面剪切作用，采用接触面单元进行模拟。

2.2.2 计算模型 将高为1 m、宽1 m、高1.5 m的长方体模型视为岩土体；对半径r为10 mm、长1.5 m的实体单元锚杆进行分析。对于锚杆与注浆体之间的锚固、破坏，采用接触面单元来达到真实的目的。具体材料参数参考算例即可。计算模型如图2；接触面单元如图3；数值模拟结果如图4、图5；计算结果如图6、图7。

图2 三维数值模拟模型Fig.2 3d numerical simulation

图3 接触面模型

图4 锚杆界面剪应力分布Fig.4 Distribution of shear stress of bolt

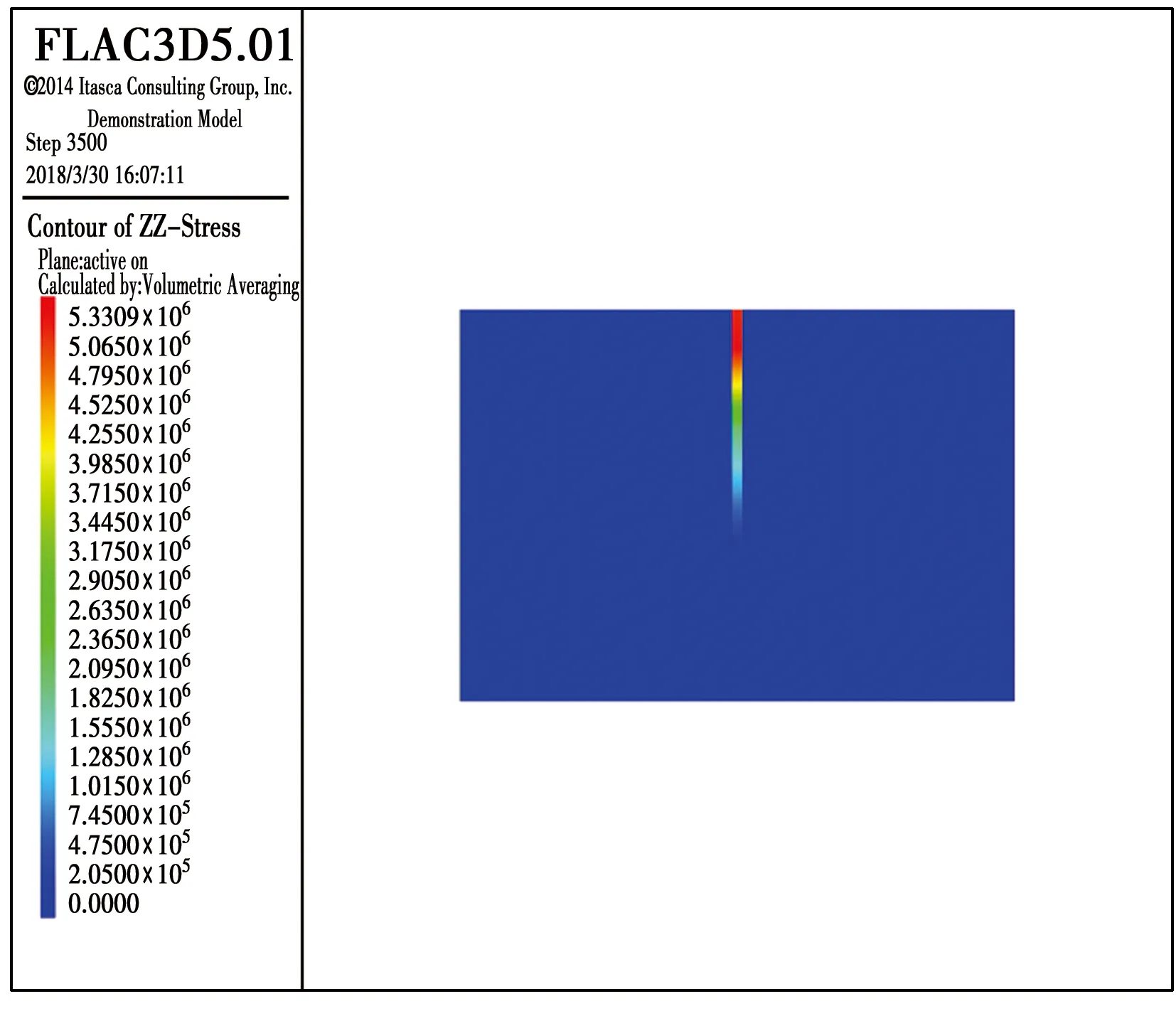
图5 锚杆轴向荷载分布Fig.5 Distribution of bolt axial

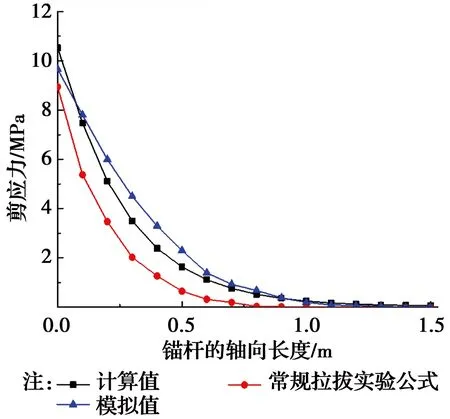
图6 锚杆界面轴向剪应力分布曲线Fig.6 Shear stress distribution curve of bolt

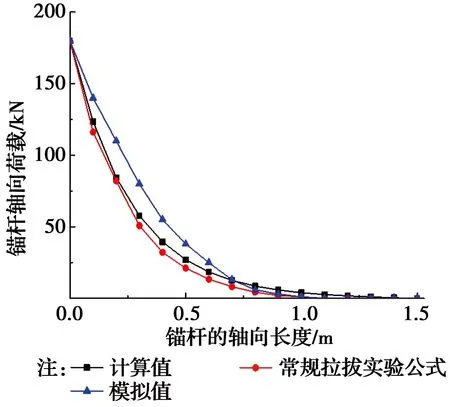
图7 锚杆界面轴向荷载分布曲线Fig.7 Axial load distribution curve of bolt

3 计算结果及分析

3.1 基本参数分析

文献[10]研究了在软岩地质条件下基于锚固体局部变形理论的锚固机理，着重研究了基于全长粘结型锚杆锚-浆破坏类型的锚固机理。把注浆体与围岩视为相对变形可以忽略的稳定体。基于锚杆与稳定体界面的相对滑移与剪切作用，式(14)中r采用锚杆半径。ks关系到公式的准确性，其物理意义是单位长度上的物质界面产生单位位移所需剪应力。日本学者尾高英雄[11]则认为，在锚固体与岩石界面发生变形时，ks包括两部分，即由注浆体变形引起的部分和岩土变形引起的部分。并认为对于岩石锚杆，岩石与注浆体的弹性模量相差度较大，把岩体当作绝对刚体，变形主要由注浆体产生。根据以上结论，本文主要研究锚-浆界面的相对滑移。由于锚杆的弹性模量远大于注浆体，故视锚杆为刚体，注浆体与围岩为共同变形的稳定体。即ks=k1，k1为注浆体剪切刚度系数。根据图6、图7可知，计算值研究的是锚杆的锚-浆破坏，在公式中使用参数r代表锚杆半径。在常规锚杆拉拔实验公式[12]中，r代表锚杆与注浆体共同形成的锚固体半径，其值一定大于锚杆半径。通过对注浆锚杆受力分析可知，在拉拔工况下，拉拔力首先作用于锚杆体上，剪应力首先产生在锚杆与注浆体的界面上，随后传播列注浆体与岩体界面上。由于两个界面的截面积并不相等，所以，其应力分布不同，故计算值剪应力略大于常规拉拔实验公式的计算值。利用数值模拟技术，根据算例的基本参数进行建模分析，得到的曲线与计算值进行对比。如图6、图7所示，经对比可以得出，三者的计算值均符合锚杆应力应变曲线规律。锚杆界面的应力分布呈非线性、非均匀分布，在锚杆距离端头长度1/3的锚固范围内，承担了约90%的应力。

3.2 影响因素分析

基于锚杆的锚-浆破坏，锚固效果主要由锚杆与注浆体之间的相互作用力承担。锚杆轴力与界面剪应力大小与分布范围代表着锚杆传递到围岩的支护反力与支护范围，是锚杆锚固效果的直观表达。根据式(12)、式(13)可以得出，影响锚杆锚固效果的变量为α、r、l。

3.2.1 锚杆长度的影响 通过改变锚杆长度，分别取1.0、1.5、2.0 m进行分析，其他参数同上，得到不同长度下锚杆体界面剪应力、轴向荷载分布函数。

l=1.0 m：

l=1.5 m：

l=2.0 m：

分析图8、图9可知：锚杆尾部存在一定的剪应力，可以通过适当增长锚杆长度达到增强锚固效果的作用。锚杆长度在一定范围内可以起到增强锚固效果的作用，但超过一定范围后，增加锚杆长度不会影响锚杆剪应力与轴向荷载的大小和分布方式的变化。

图8 锚杆轴向剪应力分布曲线Fig.8 Axial shear stress distribution curve of

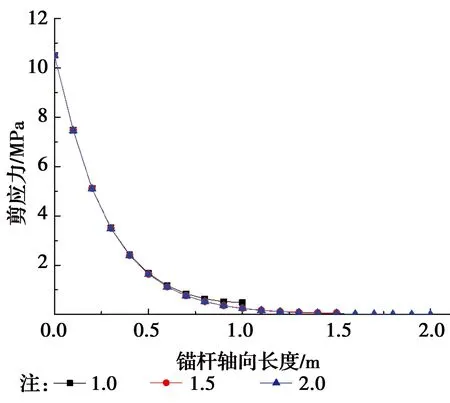
图9 轴向荷载分布曲线Fig.9 Axial load distribution

3.2.2 锚杆半径的影响 通过改变锚杆半径，取r=20、30、40 mm，其他参数同上，得到不同半径下锚杆界面剪应力、轴向荷载分布函数。

r=20 mm：

r=30 mm：

r=40 mm：

如图10所示，增大锚杆半径，界面剪应力随之减小，作用范围范围随之增大。结合图11所示，锚杆轴力分布均匀度也随之增大。结果表明增大锚杆半径可以增强锚固力作用范围，降低应力集中现象。在实际工程中应避免使用半径较小的锚杆。

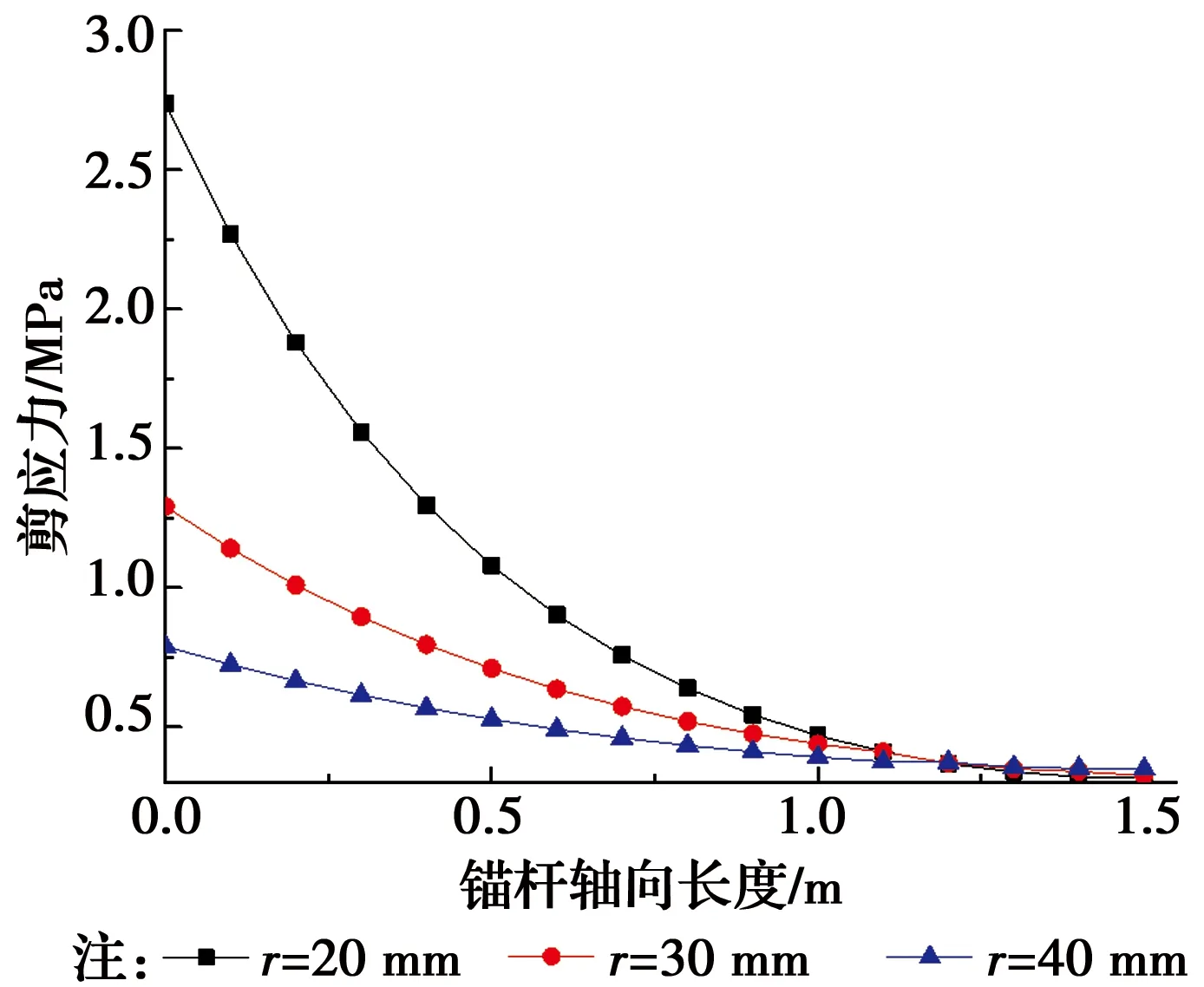
图10 杆轴向剪应力分布曲线Fig.10 Axial shear stress distribution

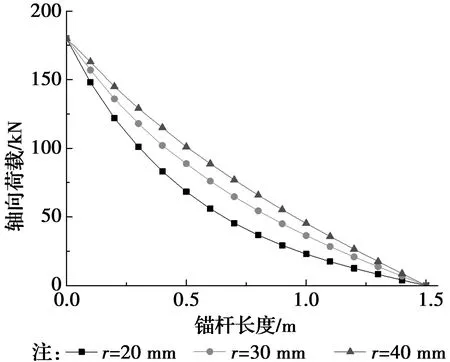
图11 轴向荷载分布曲线Fig.11 Axial load distribution

3.2.3 系数的影响 通过上文可知α2=ks/E1A1，通过改变值进行分析，在截面积A1不变的情况下，转化成对ks/E1比值的分析。ks/E1定义为表示界面材料性质的虚拟系数T，锚杆与注浆体强度相差越大，其T值越小，受双向数值影响变化。保持A1数值不变的情况下，取T=0.005 、T=0.01、T=0.02进行分析对比。其他参数同上，得到在不同虚拟系数T值基础上的锚杆体界面剪应力、轴向荷载分布函数。

T=0.005:

T=0.01:

T=0.02:

分析图12、图13可知：通过定义虚拟系数T，根据T取值大小不同，其剪应力、轴向荷载大小和分布方式不同。随着T值增加，锚杆轴向剪应力峰值增大，分布范围减小，其轴向荷载峰值强度没有变，但均匀度缩小。这说明，当两种材料强度不接近时，应力比较集中，荷载作用传递不均匀。但T值得界面数值同时影响着锚杆的极限抗拔力。可以通过适当降低T值来降低应力集中现象，增大轴向荷载作用的均匀度，以达到最佳锚固效果。

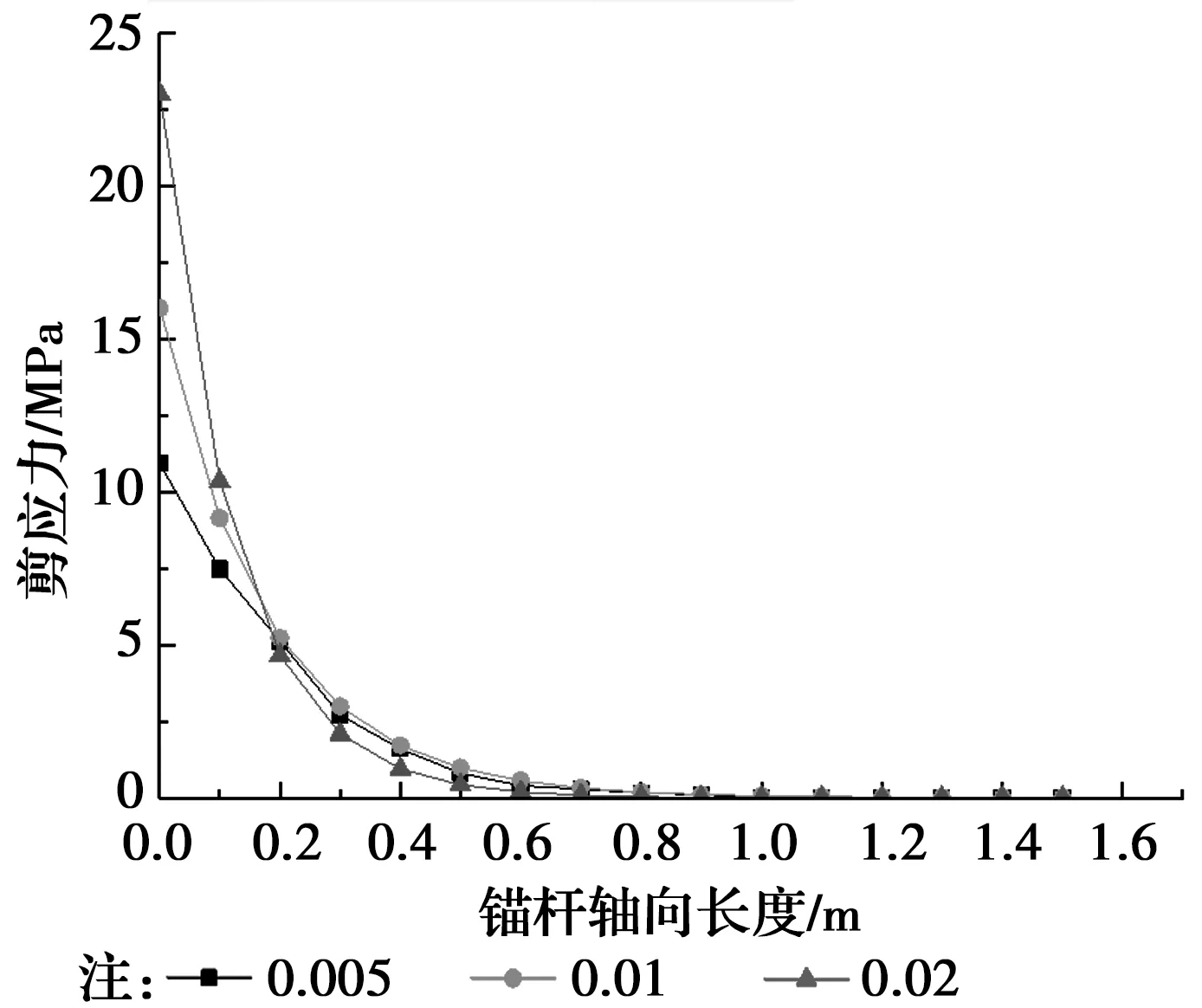
图12 轴向剪应力分布曲线Fig.12 Axial shear stress distribution

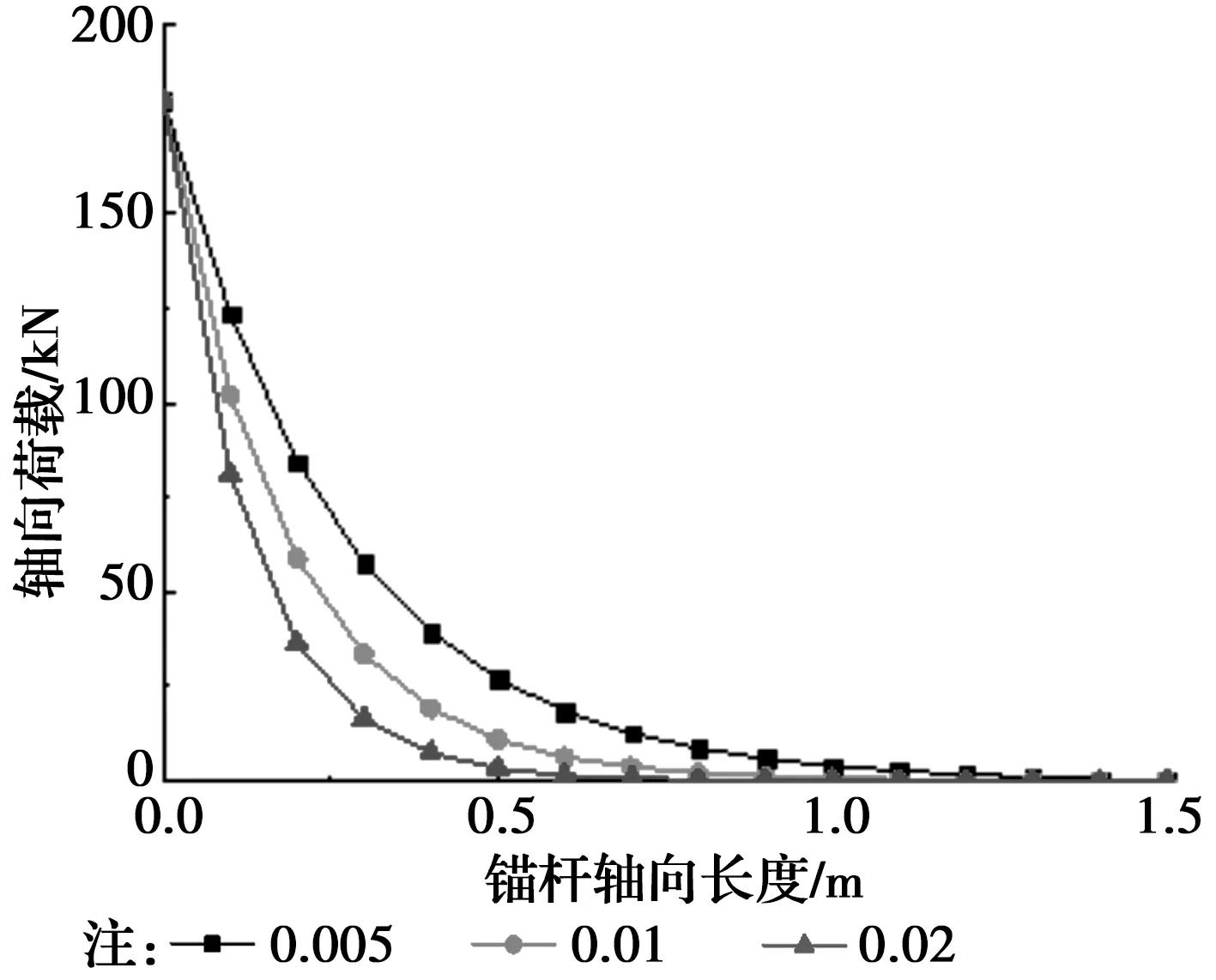
图13 向荷载分布曲线 Fig.13 Curve of load

4 结论

基于锚-浆破坏类型，分析得出影响锚固效果的数值表达式，并分析验证了相关参数的准确性及影响规律，具体结论如下：

1)通过实验公式计算和Flac 3D数值模拟技术的对比，确定了选取的r及ks参数的准确性；通过相关问题的分析计算，获得全长注浆锚杆锚-浆界面双曲线类型的剪应力和轴向荷载公式。结果表明，界面剪应力峰值处于锚杆端部，整体呈非均匀分布，在锚杆距离端头长度1/3的锚固范围内，承载了90%以上的剪切作用。

2)通过对影响参数的分析可以得到，在一定范围内，增加锚杆的长度可以增加界面剪应力的分布范围，起到增强锚固效果的作用；但过度增加锚杆长度对锚杆剪应力与轴向荷载的大小和分布方式影响不大。

3)随着锚杆体半径的增大，锚杆界面的剪应力峰值呈非线性倍增大，作用均匀度减小；轴向荷载的峰值没发生变化，但作用均匀度增大，锚杆受力分布均匀；在轴向拉力较大的情况下应避免使用半径较小的锚杆。

4)通过定义界面材料性质虚拟参数T，可以描述锚杆与注浆体强度相差度，杆体与注浆体强度相差越大，其T值越小，其值受双向数值影响变化；随着T值的增大，锚杆的剪应力峰值增大，作用均匀度减小，T轴向荷载的作用范围减小1/3；同时，影响T值的双向数值也影响着锚杆的最大抗拔力，可见T值对锚固效果影响非常明显，可以通过取适当的T值达到最佳的锚固效果。