PSO-SVM与BP神经网络组合预测供水系统余氯的方法

毛湘云，徐冰峰，孟繁艺

(昆明理工大学 建筑工程学院，昆明 650500)

氯是供水处理中使用最广泛的一种消毒剂，余氯作为衡量管网水质的一项重要指标，对控制水中的细菌滋生，保证管网水质安全十分重要。《生活饮用水卫生标准》(GB 5749—2006)[1]中规定，出厂水余氯应大于0.3 mg/L，管网末梢余氯量不应小于0.05 mg/L。但由于氯是一种非稳定性物质，受到管网中各种因素的影响，其浓度随时间的推移而发生削减，消毒能力下降，使得水质发生恶化，水质保障的中心已逐渐由水厂向管网转移[2-4]。所以探究余氯预测方法，为供水企业对氯的投加提供参考十分重要[5]。

由于余氯浓度在管网中的削减是非线性变化，且管网内影响余氯的因素众多，若采用机理性模型进行预测，其准确性差，建立难度大，求解困难[6-7]。目前已有研究多采用单一网络或复合网络对余氯进行预测，加之分析样本有限，预测后没有对结果进行误差修正，且随着样本量的增加，预测精度也随之下降，网络的精确性、收敛性及稳定性不好，难以获得理想的预测结果[5,8-9]。本文通过PSO-SVM+BP神经网络余氯预测模型，建立多个影响因素与管网末端余氯映射关系，以了解余氯的衰减规律，实现对余氯浓度的动态预测。

1 PSO-SVM与BP神经网络组合模型

支持向量机(Support Vector Machine)是基于统计学理论发展起来的机器学习算法[5]。它以结构风险最小化原则为理论基础，引入核函数方法，将原始问题映射到高维空间，把待求解问题转换为二次优化问题，使SVM收敛于问题的全局最优解。它能较好地解决小样本、非线性、高维数和局部极小点等实际问题，具有良好的泛化能力[10-12]。但SVM中关键参数(核函数参数、惩罚因子C)的选取多依靠经验或实验，而这些参数对预测的结果有至关重要的影响[13]。所以，针对SVM参数选取的盲目性，采用粒子群算法(PSO)对SVM进行参数优化，以SVM输出的均方误差为适应度函数，粒子通过跟踪个体极值和全局极值在空间内不断更新自己的位置信息、迁移方向和速度值，以寻找出空间内的最优解，即输出SVM最小均方误差时带入的参数粒子[14]，消除SVM参数选取的盲目性，但PSO算法后期收敛到一定程度时就无法继续优化，所以精度不高。为提高精度，利用BP神经网络较高的可靠性和良好的容错性，获得输入变量与优化模型预测误差之间的映射关系，建立BP神经网络残差修正模型[15-17]。最终通过两个模型的组合进行优势互补，深度挖掘数据信息，以获得更理想的预测结果，提高预测精度。

2 组合算法模型的建立

2.1 数据的筛选与处理

由于管网内余氯浓度成非线性变化，管网末端的余氯浓度，受到多种因素的影响。供水管网中余氯浓度主要受到上游监测点出厂水的余氯浓度、浊度、管网输配时间、管道内的腐蚀程度、PH值、管网材料和细菌总数的影响[18-22]。所以，从模型的普适性和对水厂的实地调研考虑[23]，取滇南某水厂2017年1月—12月份的水质检测数据，构建余氯预测模型，确定出厂水余氯浓度、PH值及浊度为影响因子，研究影响因子与管网末端余氯浓度之间的映射关系。

对某水厂的187个数据样本进行随机排列，取不同的组合方式对模型进行训练，最终确定将数据分为2部分，85%的数据作为训练数据，均分为各含有80个数据，分别建立PSO-SVM模型和BP残差模型；剩下的27个数据作为验证数据，进行交叉验证，以验证组合模型精度。末端取样点距离水厂的直线距离为2.4 km，末端余氯浓度范围为0.02～0.06 mg/L，每个样本内都含有出厂余氯浓度、pH值、浊度及管网末端取样点余氯浓度。由于数据指标不相同，数量级有一定的差别，为方便计算，需要对样本数据进行归一化处理，使数据值都归一至[0,1] 之间，归一化公式为

(1)

2.2 SVM模型的建立及优化

2.2.1 SVM模型的建立 将第1组归一化后的出厂水的余氯浓度、pH值及浊度设为输入值，管网末端出水余氯浓度作为输出值，输入到SVM模型内进行训练。首先，通过高斯径向核函数φ(x)，将训练集xi映射到高维线性空间，构造回归估计函数

f(x)=ωφ(x)+b

(2)

式中：ω为高维空间权向量；b为偏置常数。则最优问题为

yi=ωTφ(x)+b+ξi

(i=1,2,…,m)

(3)

式中：ξi为松弛因子。

因此，可以定义如式(4)所示的Lagrange函数求解上述优化问题，即

(4)

式中：αi∈R(i=1,2,...,m)为拉格朗日乘子。根据Karush-Kuhn-Tucher(KKT)优化条件得到等式(5)。

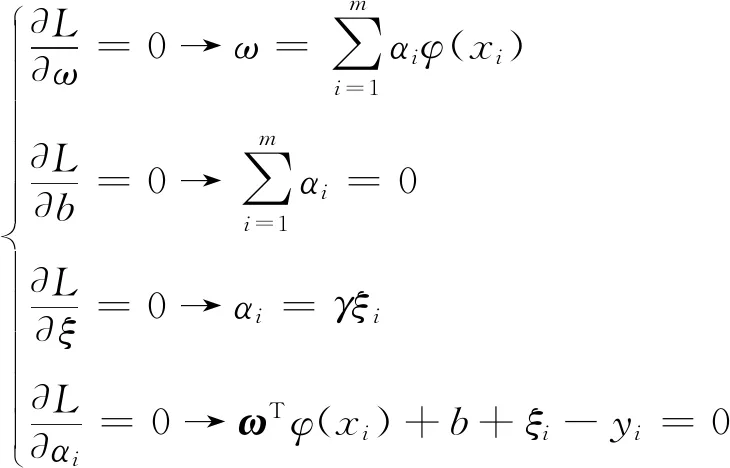
(5)

将式(5)带入式(4),将ω和ξ消去,得到线性方程式(6)。

(6)

式中：K(xi,xj)为核函数。用最小二乘法求出α和b，即得到非线性预测输出模型。

(7)

2.2.2 SVM模型的优化 对于SVM参数选取的盲目性，采用PSO算法进行优化。数据进行初始化参数设定，生成随机粒子，创建一个二维空间，粒子群规模为10。其中，第i个粒子的位置表示为向量xi=(xi1,xi2)，i=1,2,...,10。其中，xi值中包含为SVM模型的核函数参数σ、惩罚因子C，将xi带入到训练好的SVM模型中并计算出其均方误差，将均方误差作为适应度值，根据适应度值的大小评判出粒子的优劣。用向量Vi=(vi1,vi2)来代表粒子i的飞行速度，其搜索到的最优位置为pi=(pi1,pi2)，而整个粒子群搜索到的最优位置为pg=(pg1,pg2)，得到这两个最优值后，粒子就根据式(8)、式(9)进行速度和位置的更新。

vi+1=ωVi+c1r1(pi-xi)+c2r2(pg-xi)

(8)

xi+1=xi+vi+1

(9)

其中：i=1,2,...,10；ω是惯性权重函数，随着迭代的增加而减小，用来控制前面速度对当前速度的影响；设置加速因子c1=1.8和c2=1.7;r1和r2是[0，1]之间的随机数，进行50次迭代，粒子群迭代曲线如图1所示。

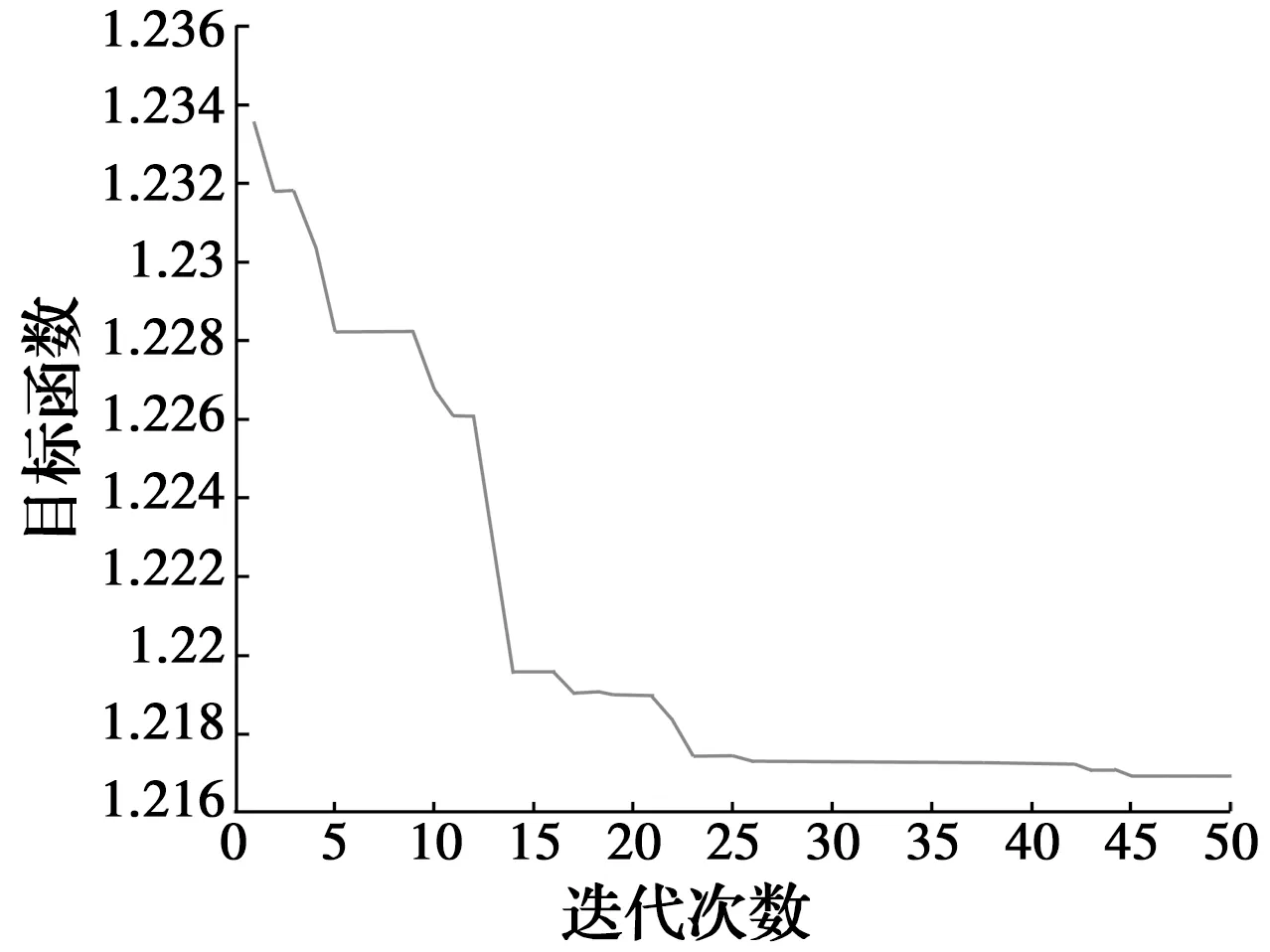
图1 粒子群迭代曲线Fig.1 Particle swarm optimization algorithm iteration

得到其最优参数为：均方误差mse=1.217，核函数参数σ=10，惩罚系数为C=6.690 4。带入SVM模型，建立PSO-SVM模型。

2.3 BP残差修正模型的建立

为进一步提高模型的精度，采用BP神经网络进行残差修正。用PSO-SVM模型对第2组数据进行预测，将预测值记录下来。以第2组数据中出厂水余氯量、出厂浊度和出厂pH值作为输入值Xi，以实测值与PSO-SVM预测值之间的偏差作为输出值Ti，组建训练样本(Xi,Ti)，建立3层前馈型BP神经网络，网络结构如图2所示。

图2 BP神经网络系统残差修正结构Fig.2 Residual correction structure of BP neural

对网络输入层、隐含层和输出层神经元之间的连接权值ωij、ωjk以及隐含层及输出层的阈值a、b进行初始化设置，然后，对模型进行训练，模型网络设置输入层到隐层传递函数为tansig函数，即

(10)

根据输入的变量Xi，输入层和隐含层间连接权值ωij以及隐含层阈值a，计算隐含层出输值为Uj。

(11)

再采用logsig函数作为隐含层到输出层的传递函数，计算BP神经网络的预测输出Gk。

(12)

用期望输出T减去预测输出G得到误差集合ek，然后用式(13)～式(16)对连接权值和阀值进行修正。

(13)

ωjk=ωjk+ηUjek

(14)

(15)

bk=bk+ek

(16)

设置输出层传递函数为logsig函数，训练函数为trainlm函数，精度取0.000 000 001，学习率为0.1%，训练次数1 000次，经过试验确定，隐含层数为16时，模型的均方误差最小，实验结果见图3。

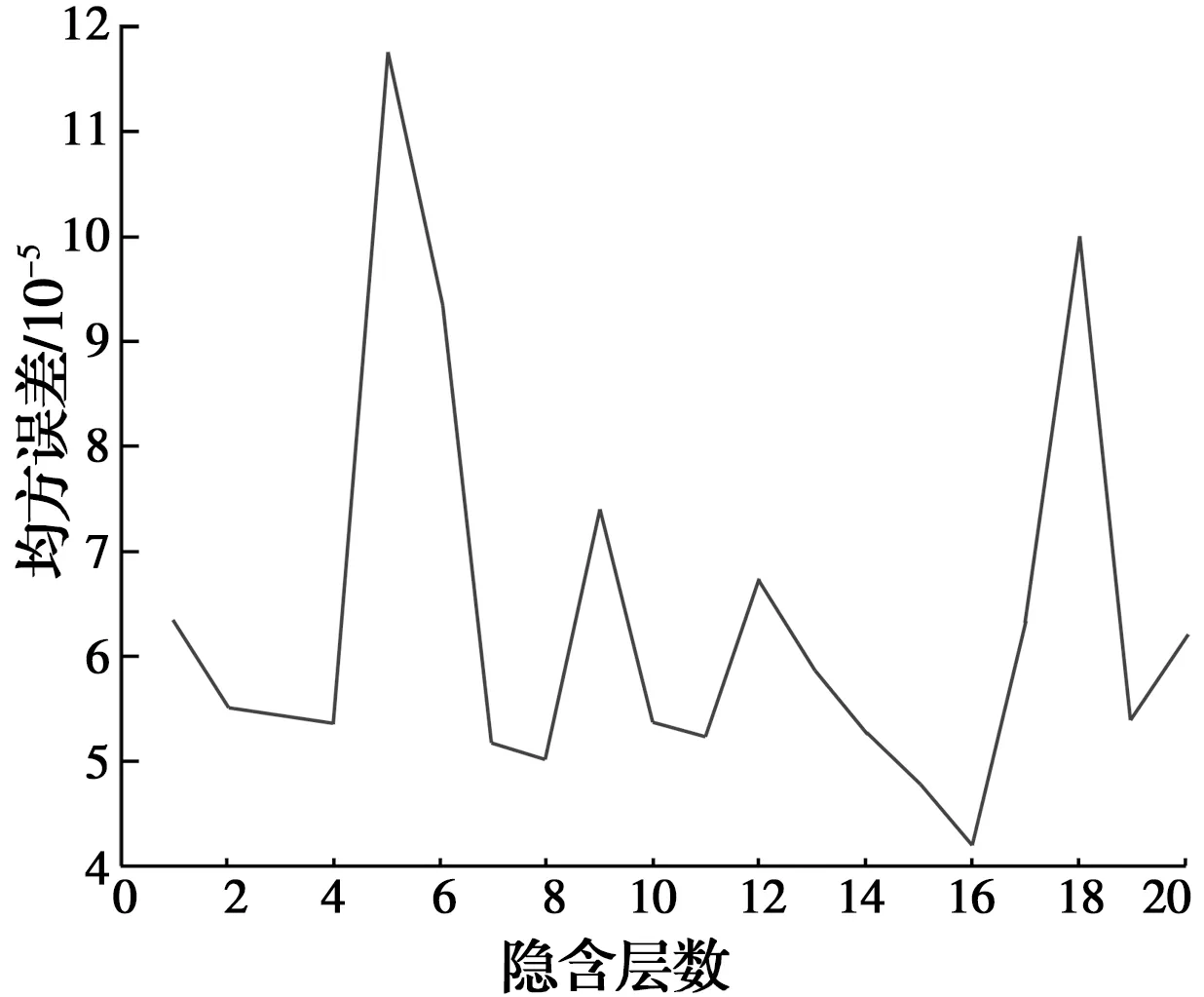
图3 组合算法不同隐含层的均方误差Fig.3 The MSE of different hidden layers in

由此建立了3-16-1结构的BP神经网络残差模型，其中，i=(1,2,3)，j=(1,2,...,16)，k=1，得出厂水的余氯浓度、pH值及浊度和PSO-SVM模型预测误差的映射关系模型，即BP神经网络残差模型。

2.4 组合模型的建立与验证

2.4.1 组合模型的建立 将第3组数据带入上述PSO-SVM模型和BP神经网络残差模型内，验证组合模型的预测效果，由PSO-SVM模型得到管网末端余氯预测值y，由BP残差模型得到残差预测值e，则最终组合模型的最终预测结果ye=y+e。如图4所示。

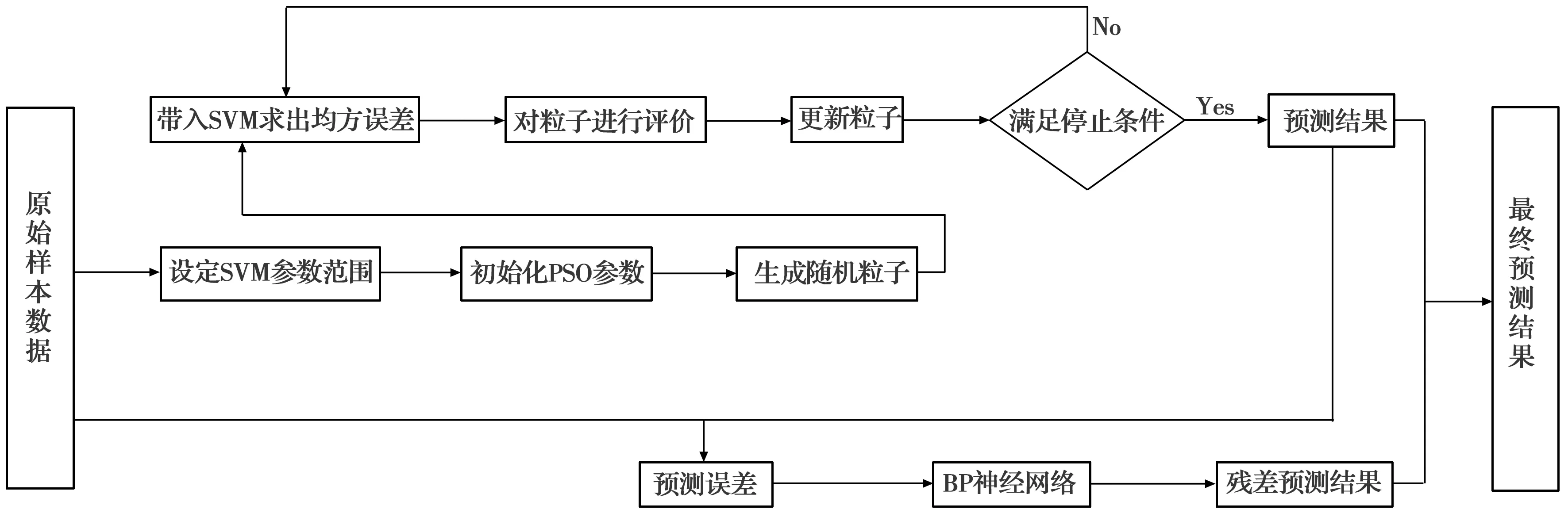
图4 组合模型结构图Fig.4 Combined model flow

2.4.2 组合模型的结果验证 将第3组数据作为预测输入组合模型，并以相同的输入输出，分别输入BP神经网络和PSO-SVM模型中对余氯进行预测，以验证组合模型的预测效果，预测结果如图5所示。

图5 各算法预测结果比较Fig.5 Prediction results comparison for different

由图5可知，单一的BP神经网络和SVM算法进行预测时，总体的预测误差较大，预测误差存在较大的波动，且对实际值拟合能力差。而组合模型的预测精度较单一模型而言有了显著的提高，具有更好的数据动态拟合能力和模型稳健性。为更直接分析模型的准确性，从图5中提取3种模型的模拟误差，见表1。

表1 模型模拟精度对比Table 1 Comparison of model simulation precision

从表1可知，单一的SVM算法与BP神经网络算法预测误差指标项相差不大，预测结果都不太理想，其均方误差分别为1.7×10-4、1.3×10-4，平均相对误差为29.13%、29.62%，相关指数R2的值分别为0.67、0.72。而组合模型经过PSO优化和BP神经网络的修正后，能够大大地提升模型性能，降低预测误差，各项指标均优于单一模型，其均方误差为4.2×10-5，平均相对误差为13.32%，相关指数R2值达到0.84。综上，组合模型对信息的捕捉较全面，总体预测稳健性较好，可以大大地降低平均误差，提升模型的预测精度。

3 结论

通过PSO算法优化SVM模型参数，并使用BP神经网络对模型结果进行残差修正，建立了PSO-SVM+BP神经网络余氯预测模型，找到多个因素与管网末端余氯的关系，通过不同模型产生的误差进行模型性能的对比分析。发现该模型可以实现对管网末端余氯量的预测，有效地简化了余氯在管网中衰减变化的复杂非线性关系，克服了SVM模型参数选择的盲目性，利用BP网络对结果进行优化，进一步提升了预测的精度和模型运行的稳健性。结果表明，该模型具有良好的预测性能，能够使供水企业更早地发现水质恶化的趋势，及时采取相关措施，在控制末端水水质的前提下，降低消毒副产物的产生，并为二次消毒点的选取提供参考。