初中生“几何推理”的初学困境浅谈

唐开杨

摘 要 本文从初中学生的认知起点和最近发展区入手，以教学一线中遇到的实际问题为载体，总结梳理了初一学生在初学“几何推理”时所遇到的三个认知瓶颈，并给出了可操作的解决办法，最后提出了笔者关于“几何推理”教学的一点思考。

关键词 几何推理;初学;困境

中图分类号：G632 文献标识码：A 文章编号：1002-7661（2019）05-0142-02

推理，思维的基本形式之一，由一个或几个已知的判断（前提）推出新判断（结论）的过程。几何推理就是在几何图形中根据一些条件推出结论的过程，学生几何推理能力的提升与“逻辑推理”、“直观想象”两大核心素养的落地有着极其密切的联系。

一、问题提出

进入初中学习后，学生的数学学习学业水平的第一个分水岭出现在学习“几何推理”之后，以北师大版初中数学教材为例，学生在七年级下第二章《相交线与平行线》的学习之后开始出现分化，七年级下第四章《三角形》的学习之后分化进一步加剧，其结果直接导致七年级下的数学学业成绩相较于七年级上在平均分控制的前提下其极差与方差都有显著性增大。

林崇德将中学生“空间想象能力”分为三级水平，而初中一年级的学生其空间想象能力处于第一级水平向第二级水平过度的阶段，因而，教师要能够发现这个阶段学生在认知发展上的困境，并给予有针对性的帮助，使学生能够顺利从第一级水平进阶到第二级水平。

二、三重困境及应对策略

笔者在长期的一线教学过程中，发现七年级学生在初学几何推理时主要有以下三重困境：

第一重困境：文字概念的核心要素與图形基本型之间的转换。

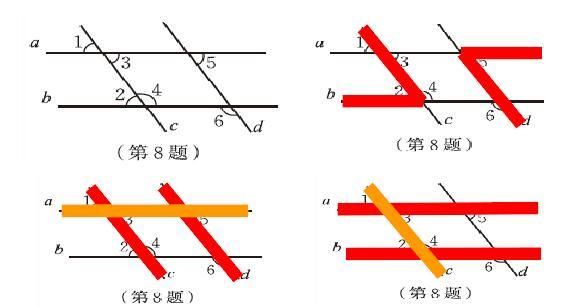
以北师大版七年级下册数学教材P59第8题第（2）问为例，如果希望c∥d，那么需要哪两个角相等？

题目原图，错解1：∠2=∠5

错解2：∠3=∠2，正解1：∠4=∠6

有趣的是，如果你追问答错解1、2的学生为何选这两个角？

学生会肯定的告诉你：内错角相等，两直线平行。可见，学生并非是对平行线的判定定理不理解，而是对“内错角”的概念理解出了偏差。课本P47关于“内错角”的概念是如此说明：“具有∠1与∠2这样位置关系的角称为内错角”。

参考人教版教材七年级下，教师一般会辅以文字说明：直线AB、CD被直线l所截构成8个角，在直线AB、CD之间，并且分别在直线l两侧的一对角叫做内错角。

可见，学生出现问题的主要原因是对“内错角”概念的前提理解不到位，当这个前提以文字形式出现时，学生不能把此核心要素转化成三线八角的基本型并从复杂图形中提取出来。要解决这个困境，在教学中教师首先要重视几何概念的生成过程，如学生不体会生成，便无法理解文字，更不用说将文字和复杂图形间建立联系;其次，要引导学生将图形和文字，文字和图形进行双向对应的技能训练。

第二重困境：图形解构过程中对图形已知的提取与应用。

当学生从平行四边形学习到封闭图形三角形的时候，其既需要对三角形的整体认知，又在很多情况下需要解构三角形，分别研究三角形的边或者角。此时，解构过程中对图形已知的提取，明显难于对文字或符号语言所给出的已知条件的提取。

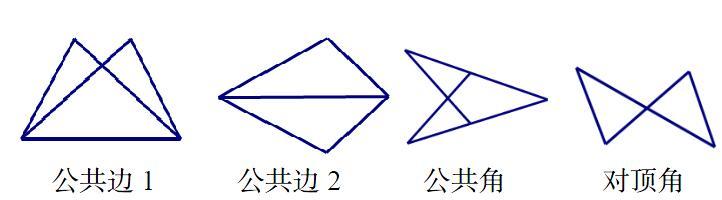
三种常见的图形已知如下：

公共边1      公共边2      公共角       对顶角

经过一定的训练，以上四种直接给出的图形已知，学生能够理解并很好的掌握，但是，当图形出现变化或更加复杂的时候，能否将图形进行解构，拆解出的熟知的图形已知，就成为了突破的关键。

以北师大版七年级下册数学教材P111第7题为例：如图，AB=AD，AC=AE，∠BAE=∠DAC，△ABC与△ADE全等吗？

若学生无法解构图形，将△ABC和△ADE分离出来，那么他就无法将符号已知∠BAE=∠DAC与图形已知∠EAC=∠CAE联系起来。可见，学生初学几何推理时面对的这个困境首先要具备解构复杂图形、分离基本图形、抽取核心要素的能力，教师可以四种常见图形已知为蓝本，进行变式训练，帮助学生渡此困境。

第三重困境：文字语言、符号语言、图形语言的三重转换。

从学生一开始学习“几何推理”，教师就会不厌其烦地在各种定义、定理的教学中，在各类习题的讲评中渗透文字语言、符号语言和图形语言的三重转换，但教师往往只重视纯数学问题中的转换，所以文字语言与两者之间的转换常常是训练不到位的，同时也直接影响了学生应用数学解决问题的能力。

以北师大版七年级下册数学教材P111第11题为例：

工人师傅经常利用角尺平分一个任意角。如图所示，∠AOB是一个任意角，在边OA、边OB上分别取OD=OE，移动角尺，使角尺两边相同的刻度分别与D、E重合，这时过角尺顶点P的射线OP就是∠AOB的平分线，你能先说明△OPD与△OPD全等，再说明OP平分∠AOB吗？

很明显，教材编写者已经将问题拆解为两步，刻意降低了问题的难度，搭建了台阶。但是在实际教学的过程中，仍然有不少的同学无法完成。究其原因，主要是无法将“移动角尺，使角尺两边相同的刻度分别与D、E重合”这句话结合图形转换成符号语言。如果我们将此题抽去实际背景，直接以符号语言给出已知、求证，学生的回答正确率就会大大提升。

这一认知瓶颈提示我们，在进行几何推理的教学时，一定要兼顾学生现有的生活经验和认知水平，既要有纯几何的熏陶，更要有实际问题的锤炼，条件允许的情况下要让学生多操作，比如让学生自制角尺，模拟操作等。在初学阶段，大部分的问题都还停留在“简单”的层次，是训练三种语言转换，提升互译能力的大好时机，确保进入更为复杂的几何推理学习之前，各个层次的学生的互译能力都有提升。

三、关于“几何推理”教学的一点思考

（一）“几何推理”不仅是学生初中阶段数学学习的第一个分水岭，也是教师教学能力分化的一个分水岭，一个优秀的数学教师，不应该任由学习能力相对较弱的学生在此处分流，而应该多探究现象背后的原因，并积极寻找解决的办法。

（二）7年级学生的几何能力和几何直观推理意识快速增强，7下更是他们这种能力发展的关键期，教师要提供尽可能多的实验操作机会辅助学生判断和推理，既要尊重他们现有的形象思维的认知现状，又要不遗余力地引导他们向抽象思维的最近发展区进军。

（三）尊重学生的个体差异，尤其在几何推理方面，男女生有显著的差异，男生发展迅速但结束期早，女生发展缓慢但持续时间长，教师应对此特点有所认识并给予耐心的呵护，使每一位学生都能在数学学习上有所发展。

参考文献：

[1]李红婷，初中生几何推理能力发展研究，教育研究与实验，2009（1）.