解答数学选择题要“不择手段”

☉山东省济南市莱芜区雪野镇中心中学 王青山

选择题，不需要完整、详细的解答过程，既然正确答案就摆在眼前，我们为了选出它，就可以“不择手段”.很多选择题是不用直接解答就能得到正确答案的，有很多巧妙的方法，既简单又高效.因此我们解答选择题时，方法要灵活多变，能根据题意随机应变地处理，很多时候会事半功倍.

一、赋值法——解含有未知参数的问题

例1当k＞时，直线kx-y=k与直线ky+x=2k的交点在（ ）.

A.第一象限 B.第二象限

C.第三象限 D.第四象限

正面解答过程分析：解方程组，得两直线交点的坐标为.因为，所以

所以交点在第一象限.

赋值法解答过程分析：令k=1，可得方程组

所以可得出交点在第一象限.

解法对比分析：正面解答的过程，要经历解二元一次方程组，而且方程组中含有参数k，所以解答过程并不是很简单，费时费力.而且解完方程组后，还要根据k的取值范围确定两个式子的符号，思维量、计算量明显很大.如采用赋值法，方程组中不再含有参数k，方程组解起来简单、明了，计算量明显减少了很多.

解题启示：题目中如果给出一些开放性的条件，特别是含有一些未知参数的信息，而问题的答案是固定的，这时我们可以采用赋值法，给定参数一个合理的取值，让未知参数问题变成已知参数的问题，使问题变得具体、简单.

二、排除法——解选项之间自相矛盾的问题

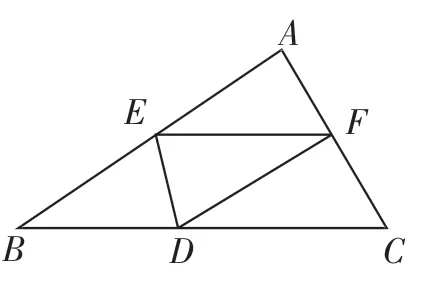
图1

例2如图1所示，已知△ABC中，BC=12，BC边上的高h=6，D为BC上一点，EF∥BC，交AB于点E，交AC于点F，设点E到边BC的距离为x.则△DEF的面积y关于x的函数图像大致为（ ）.

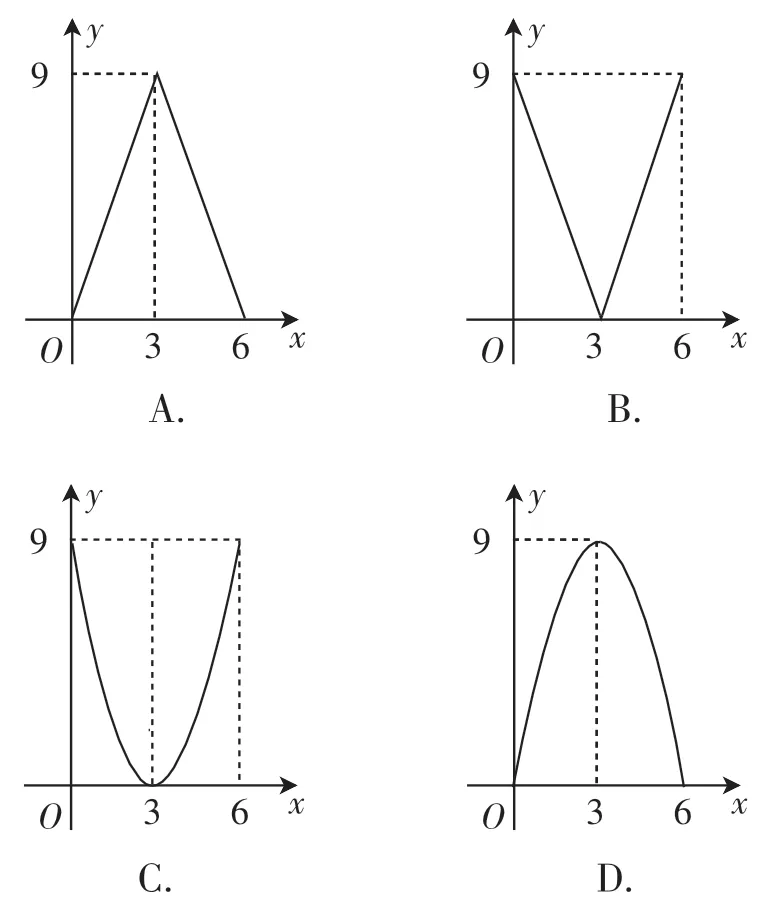
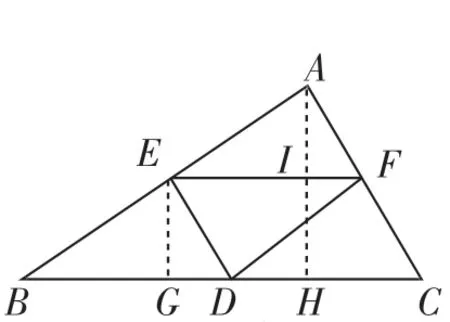
图2

正面解答过程分析：如图2，作EG⊥BC，AH⊥BC.易得AI=6-x.由EF∥BC，可得△AEF?ABC，所以即，可得EF=12-2x.所以S△6x.由二次函数图像的性质可得出正确选项是D.

排除法解答过程分析：观察四个选项，选项A、B与选项C、D之间有函数类型不一致的矛盾，所以确定了函数类型就能排除掉两个错误选项.理解题意，在运动变化过程中，底EF的长度与高EG的长度都在改变，△ABC的面积与EF、EG的乘积相关，所以初步判断面积是关于x的二次函数，排除选项A和B.选项C、D之间的矛盾可利用x=3排除.结合已知条件，当x=3时，EF是△ABC的中位线，此时△DEF的面积是9，所以选项D是正确的.

解法对比分析：正面解答的过程，要求学生通过构造相似关系构建函数模型，对学生的数学思维能力和知识应用能力有较高要求.采用排除法，学生利用三角形的面积公式可粗略判断出函数的类型，从而排除错误选项，再结合特殊值即可选出正确答案.综合对比，运用排除法，在解题的速度和准确度上更胜一筹.

解题启示：当我们遇到选项之间有矛盾存在的题目时，可以利用条件找出矛盾的根源，做出初步判断后排除干扰选项，以此减少我们的计算量，提高解题的效率.

三、代入验证法——解“二选一”还是“二选二”的问题

例3已知关于x的一元二次方程0有两个不相等的实数根x1、x2.若，则m的值是（ ）.

A.2 B.-1 C.2或-1 D.不存在

正面解答过程分析：因为方程有两个不相等的实数根，所以Δ＞0，即，解得m＞-1.又根据条件，利用根与系数的关系，解得m1=2，m2=-1.

综上所述，m的值为2，正确选项是A.

代入验证法解答过程分析：观察四个选项，显然是在2和-1这两个数之间做选择，我们可以分别将2和-1代入方程的根的判别式验证一下.将m=2代入，得到Δ=12＞0，符合题意；将m=-1代入，得到Δ=0，方程有一个相等实根，不合题意.所以正确答案是A.

解法对比分析：正面解答的过程，需要学生有一些一元二次方程的有关知识储备——根的判别式、根与系数的关系等知识，此外要经历一些解方程和不等式的计算过程，要求学生具备一定的计算能力和逻辑思维能力.如果采用代入验证的方法，只要代入两次值，就可以做出正确的判断.

解题启示：当我们遇到答案是在几个具体的数值之间进行选择的时候，根据条件可以将几个值分别代入原题，再做判断，给解题带来方便.

当然，方法是死的，人是活的，具体问题还是要具体分析.学习数学本身就没有一成不变的套路.以下三题留给读者品析.

牛刀小试：

题1：如图3，函数和的图像分别是l1和l2.设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则三角形PAB的面积为（ ）.

A.2 B.4 C.8 D.无法确定

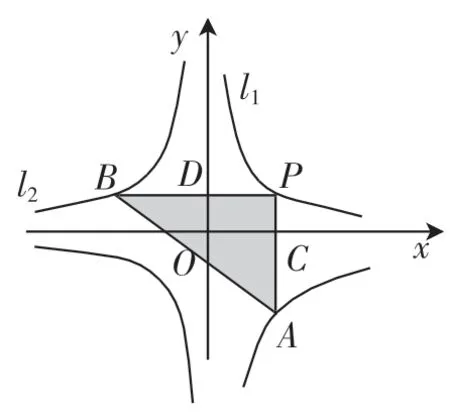
图3

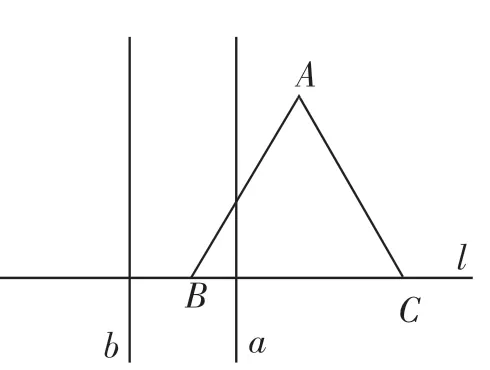
图4

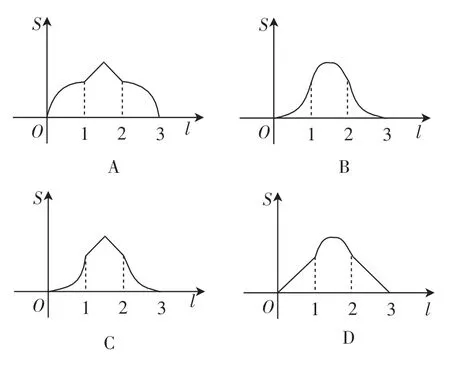
题2：如图4，边长为2的正△ABC的边BC在直线l上，两条距离为1的平行直线a和b垂直于直线l，a和b同时向右移动（a的起始位置在B点），速度均为每秒1个单位，运动时间为t（秒），直到b到达点C停止，在a和b向右移动的过程中，记△ABC在a和b之间的部分的面积为S，则S关于t的函数图像大致为（ ）.

题3：关于x的方程x2-ax+2a=0的两根的平方和是5，则a的值是（ ）.

A.-1或5 B.1 C.5 D.-1

师者，传道授业解惑.为人师者，除了教会学生知识和学习的方法，在现行教育体制下还要教会学生考试的方法.如果思维灵活了，方法多变了，不仅会给学生带来解题上的快感，增强学生考试的信心，还能让学生提高效率，节约出一部分时间去思考难题，从而在一定程度上提高学生的考试成绩.这于学生、于老师未尝不是一件幸事！