“留白式”活动单：让合作学习走向深入

☉江苏省如皋市白蒲镇阳光初级中学 陈志勇

活动单导学在本地区已推行十多年，不同学科在设计“活动单”上也积累了丰富的经验.笔者所在学校经过实践、反思与改进，通过研发“留白式”活动单促进合作学习走向深入.本文结合典型案例，介绍“留白式”活动单的研制与教学意图，提供研讨.

一、用留白式问题情境，引导学生参与新概念的归纳

李邦河院士说“数学，根本上是玩概念的，技巧不足道也.”数学教学从根本上说也是玩概念的，概念有一种形式是新数学对象如何进行定义，定义最重要，因为定义是“双向”的，可以作为性质使用，也可以作为判定使用，所以定义在解题中是最有力量的，人们常常说“回到定义去解题”说的就是这个道理.所以在概念教学时，要注意引导学生参与新概念的归纳、生成定义的过程.

案例1平行四边形（第1课时）开课阶段

问题1：四边形是如何定义？

图1

问题2：如图1，这个四边形有什么特别的地方？

问题3：你觉得怎样给平行四边形下定义？自己写一个定义，然后小组内交流讨论.

贵州省某磷复肥企业负责人告诉记者，目前开磷集团和瓮福集团的融合在技术层面是可以实现的，比如磷石膏的处理技术已经成熟，但是是否能真正实现生态效益和经济效益双丰收，在何光亮面前仍有较大阻碍。他说：“两家企业都是国有老牌企业，负债率都比较高，而且企业包袱重，所以首先要解决资金问题。如果资金瓶颈无法解决，后续很多想法是难以落地的。另外是市场的问题，磷石膏绿色建材的发展思路固然很好，但是目前市场不成熟，有待开发。”

教学意图：这是平行四边形定义教学时留白式活动单，注意区别于有些学案上给出填空式，比如平行四边形定义：“两组对边分别______的四边形，称为___________”.通过3个问题串，促进学生自主研究平行四边形的定义，并小组内合作讨论得出平行四边形的定义.特别是“问题2”暗示了“问题3”的定义，使得学生在各自写出定义之后，小组内合作讨论时需要辨析定义是否精当，因为定义无需证明，但是定义可以作为后续平行四边形的“第一性质”或“第一判定”.

二、留白实验演算活动，引导学生合作探究新的性质

数学教学过程中有很多新的性质、法则需要通过推理演算归纳发现，而不是“一个性质、三项注意、大量练习”式的教学方式.不少老师设计出一些实验操作、演算归纳的数学活动，引导学生发现新的性质，这种做法是值得肯定的.但是由于活动单上这些实验或演算的步骤过于密集，使得学生的合作没有走向深入.

案例2探究“不等式的性质”

“演算实验1”：已知2＜3，比较：2+5___3+5，2+20___3+20，2+29___3+29；

2-3___3-3，2-6___3-6，2-2019___3-2019；

再举一些算式运算并比较，已知5＜6，比较：…….

你能发现怎样的规律？请选用一句话概括，并在小组内交流讨论.

“演算实验2”：已知3＜5，计算并比较：3×2020___5×2020，3×___5×；

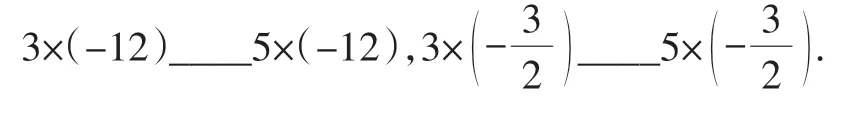
再举一些算式运算并比较，已知-3＜-2，比较：…….

你能发现怎样的规律？请选用一句话概括，并在小组内交流讨论.

教学意图：教材上也是给出了一些算式安排学生运算后发现规律，并归纳出不等式的性质，再进行运用.我们对演算实验进行了改编，将不等式性质的实验发现适当留白，引导学生参与举例，这样所举出的一些算式是随意的，而且各个小组也“各不相同”，有利于在随后的分组展示时看到大家的不同实验，但都“指向”共同的规律，加深学生对不等式性质的理解和信任.当然，在归纳出不等式性质的基础上，如果能跟进不等式性质的“证明”（比如，利用数轴上两点的平移验证或利用“作差法”进行证明），就更能传递数学的力量感了.

三、例题教学适当留白，引导学生深入研究回顾反思

数学课堂一般都离不开例题教学，但是例题并不能只是满足于教师讲解.如何促进学生思维参与，让学生小组内分工合作研究不同解法，也是值得我们在解题教学前认真构思的.

案例3正方形为背景的例题教学

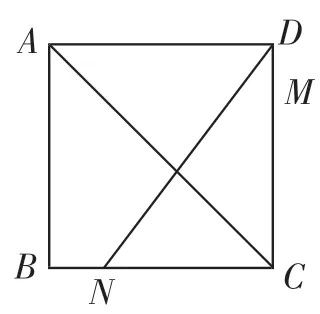
图2

如图2，边长为4的正方形ABCD中，点M在边CD上，M，N两点关于对角线AC对称.设DM=1.你能设计一个怎样的问题？

预设追问1（PPT呈现，活动单上不显示）：在AD上找一点P，使△PMN的周长最小；

预设追问2（PPT呈现，活动单上不显示）：求tan∠AND的值.（用两种方法）

预设追问3（PPT呈现，活动单上不显示）：设AC，DN交于Q，求AQ的长.

预设反思问题（PPT呈现）：解答这道问题之后，你觉得哪个问题给你留下较深的印象，在小组内交流一下，然后选一个代表进行全班展示.

教学意图：解题教学时，如果把一道综合题（含系列设问）整体呈现在学生的活动单上，则有些优秀学生往往会埋头攻克系列问题，而缺少课堂上的合作研究、交流展示、倾听评析，而当我们在活动单上只给出例习题的“题干”部分，让学生看不到后续设问，先安排学生进行自主设计、小组交流，再大组展示，则可促进学生参与课堂.在此基础上利用PPT的渐次呈现功能，依次出示追问，可以有效组织学程.特别是，解题教学之后需要有必要的回顾环节，引导学生回顾习题解法的关键步骤，习题的深层结构，习题还可能有怎样的变式拓展，习题还可以怎样设问呈现，等等，这些角度的回顾反思都可促进学生“解一题、会一类、通一片”.

四、小结预设留白问题，安排学生合作梳理本课所学

课堂小结一直是教研的一个薄弱环节，很多课堂因为习题容量太大，使得课堂小结流于形式、匆匆带过.课前需要精心预设留白问题，以便让学生分组合作梳理本课所学内容，做到重点复述，难点再过一遍，所学新知梳理成框架、结构化理解.

案例4三角形（第1课时）小结阶段

小结问题1：本课主要学习了哪种图形？你是怎么理解它的定义？

小结问题2：这节课我们在研究三角形时，是从哪些角度展开的？

小结问题3：用结构图梳理本课所学内容，在小组内交流，推荐一个较好的新知结构图上台投影展示并介绍.

教学意图：有些课堂小结往往是泛泛而问“这节课学到了什么？”“这节课你收获了什么思想方法？”等，问题空、泛，小结过程成为形式，学生没有兴趣.通过精心预设小结问题，可以引导学生回顾本课所学，并构建结构图来梳理所学，在小组内还要展评、推荐展示，可以促进学生参与和激发兴趣，也增加了学生上台展示的机会.

五、研发留白式活动单的一些体会

经过一段时间的实践，目前笔者所在学校在集体备课时都要精心打磨留白式活动单，往往都是先由主备人出示一份内容详实、容易偏大的初稿，然后在此基础上进行删减、留白，参与者认真打磨、优化设问，并将相关内容隐藏、放置到PPT相应页面留作课堂上渐次呈现、详细追问.在这个过程中，集体备课尤为重要，因为要集全组成员的智慧进行研发，不只是教学内容的取舍、删减，而且是基于学情的教法研讨，使得“教什么”“怎么教”得到充分的预设，在这个过程中，年轻教师更能得到很好的专业成长.

此外，留白式活动单也有效地改变了课堂上学生的参与状态.过去当出现一些“大容量”的活动单（往往以密集呈现习题或是摘抄自教材的一些知识或梳理）时，很多学生从开始上课就盯着自己的这份活动单，埋头苦做，一些优秀学生在老师讲评时也不抬头，似乎数学课就是认真刷题，数学课堂的品质也大打折扣，不利于优秀学生对数学的理解.通过留白式活动单，向学生传递“数学追求简洁，数学习题追求成果扩大”的思想，通过回顾反思促进学生洞察问题深层结构，通过学生小组合作学习培养学生善于倾听并分享到小组成员的精彩观点，也是“让学”（海德格尔）理念的真正实践.