横向液货补给系统软管静力学分析
2019-08-31李健康任爱娣何学军
李健康, 任爱娣, 何学军
(海军勤务学院, 天津300450)
0 引 言
海上航行横向液货补给是海上液货补给作业最常用的一种补给方式,具有补给种类多、补给效率高等优势,在世界主要国家的海军液货补给中占据主导地位[1]。输送燃料、淡水等液货的补给软管是航行横向液货补给系统的重要组成部分,其受力状况直接影响补给作业的安全和补给效率。研究补给软管的静力学特性,不仅有助于提高补给作业的安全可靠性,还能够为补给装置系统的设计研发提供必要的技术支持和理论依据。
由于应用范围较窄和军事保密等原因,有关横向液货补给系统研究的文献相对较少,而且多在工程应用领域。安德列耶娃等[2]从结构设计制造的角度,系统地介绍了包括横向液货补给系统在内的各种补给装置的技术参数和设计原理,并给出补给软管张力的经验计算公式;宇可等[3]根据该经验公式,计算论证了一种适用于小型舰艇和民船的横向液货补给装置的可行性;余建星等[4]简单论述海上液货补给装置的历史与发展,提出各类液货补给方式的优缺点,严梅剑[5]对海上航行横向补给装置的的选型作了相关介绍,但两者都未涉及理论层面;翟性泉等[6]从工作原理、技术层面上介绍了一种直接利用补给软管承载液货重力的新型横向液货补给装置;王琦等[7-8]基于悬链线理论对该装置补给软管承载力进行分析计算,但给出的计算公式实际上也是基于抛物线理论的近似结果。综上所述,对于横向液货补给系统补给软管的研究主要停留在技术应用层面,所给出的计算公式多是经验公式,不能很好地满足现实需求。
本文采用更符合补给软管实际线型的悬链线理论建立补给软管的力学模型,得到补给软管的线型函数式,通过数值计算的方法分析补给软管的挠度曲线、曲率半径变化曲线和张力分布曲线,并且探讨最小曲率半径和最大张力的影响因素。
1 力学模型
1.1 基本假设
补给软管在补给作业过程中处于悬垂状态,其受力状态类似于受自重作用的悬索,可采用悬索理论进行分析。目前应用较多的悬索理论主要是抛物线理论和悬链线理论,由于悬链线理论关于悬索竖向荷载沿索弧长均匀分布的假设更接近补给软管的实际状态,且对存在一定挠度的悬索具有相对更高的计算精度,因此采用悬链线理论进行计算分析更合适。
为了便于建立悬链线方程,在不影响问题研究的基础上,对软管作如下假设:
(1) 假设在液货补给过程中,补给液货始终充满软管,管径相同,软管的重力均布荷载沿管长不变。
(2) 假设拉伸形变较软管长度很小,忽略补给软管的拉伸形变影响。
(3) 假设软管是理想柔性,只承受拉力,不承受压力和弯矩。
(4) 在补给过程中,补给船与接收船以相同速度同向航行,假设补给软管始终处于同一平面内。
1.2 悬链线方程建立
在实际横向液货补给过程中,补给软管通常由鞍座分段连接形成液货输送管路,取介于鞍座与鞍座之间的单段软管为研究对象,如图1所示,以软管较低端为坐标原点建立直角坐标系,假设补给软管AB的水平跨距为l,高差为h,弦倾角为θ,重力均布荷载为q。取软管上任意微段ds进行静力学分析,如图2所示。
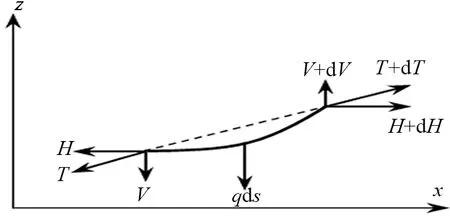
图2 软管微元受力分析
假设补给软管受到张力T的水平方向分力为H,竖直方向分力为V,则通过静力学平衡方程得
∑X=0,dH=0
(1)
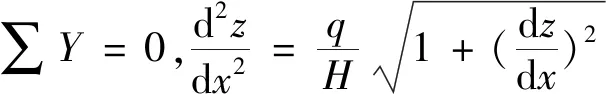
(2)
由式(1)可知,在悬垂状态下,补给软管张力T的水平方向分量H大小恒定。对式(2)进行积分求解(过程略),并根据边界条件:x=0,z=0;x=l,z=h,得到补给软管的悬链线方程[9]为

(3)
式中:α、β为所设参数值,其大小由式(4)确定:
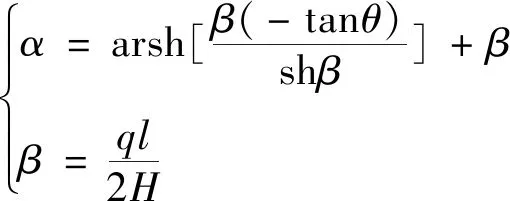
(4)
2 补给软管线型分析
在液货补给作业过程中,为保证安全,应避免补给软管落入水中,补给软管的最低点位置需重点关注。设C点是软管AB的最低点,对式(3)求导取极值点,最低点C处横坐标为
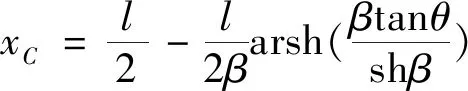
(5)
将式(5)整理后代入式(3),得到已知最低点条件下的补给软管线型函数式为

(6)
2.1 补给软管长度计算
设补给软管的长度为S,由弧长计算公式可知,软管的长度等于对线型曲线弧长的积分,即
利用双曲函数的和差公式整理式(7),得到软管的长度计算式为
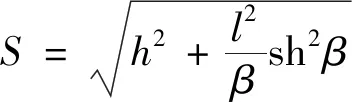
(8)
分析式(8)可知,在高差h和跨距l已知的条件下,管长S是参数β的函数,若已知管长,可通过数值求解得到参数β的值。
2.2 软管挠度分析
根据挠度的定义式f=z0-z,将式(6)代入其中,则补给软管的挠度函数式为
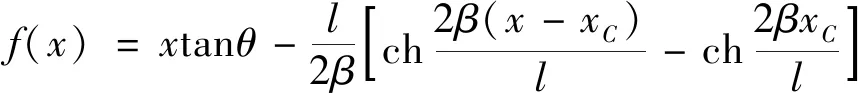
(9)
在通常情况下,补给软管的长度和单位荷载集度是已知的,补给软管的高差和跨距可根据实际情况取值,假设l=15 m,h=4 m,S=20 m,q=200 N/m(除可变参数外,下文数值计算均采用此数据),将上述参数代入式(8)中求解得到参数β值,根据式(4)可知最低点位置发生在x=6.33 m处,通过进一步的数值计算得到补给软管的线型曲线和挠度曲线如图3所示。由图3可知挠度曲线近似关于跨中位置x=7.50 m对称,对式(9)求导取极值点,得到最大挠度点发生在x=7.85 m处,显然在软管两端不等高情况下,最大挠度点和最低点位置不重合,只有当两端齐高时,挠度曲线和线型曲线关于x轴对称,挠度最大值和最低点值重合在跨中位置,因此文献[7]在不等高的情况下,采用最大挠度位置代替最低点位置计算会产生一定偏差。
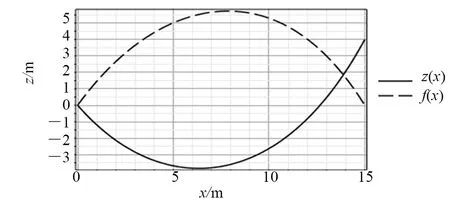
图3 补给软管线型曲线和挠度曲线
2.3 软管曲率半径
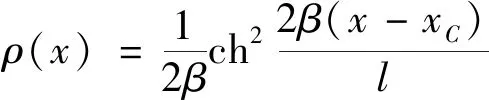
(10)
对式(10)进行数值求解,得到曲率半径随横坐标变化曲线,如图4所示。由图4可知,曲率半径随横坐标的增大呈先减小后增大趋势,存在极小值,曲率半径最小值产生在极值点处。

图4 补给软管曲率半径变化曲线
2.4 软管张力
设软管任意位置P(x,y)点的张力为T,张力的竖直分量为V,通过静力学分析可知:

(11)

(12)
代入参数进行数值求解,得到软管张力变化曲线,如图5所示。由图5可知,补给软管的张力沿最低点位置向两端逐渐增大,最小张力位于补给软管线型最低点处,最大张力在较高端的端部位置。
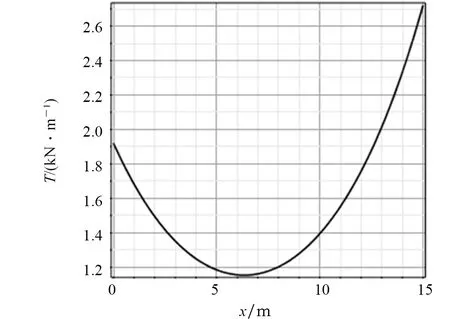
图5 补给软管软管张力变化曲线
3 补给过程安全性分析
为保证补给作业安全、高效进行,需采取有效措施控制软管曲率半径和张力,保证其满足限值要求,需对软管最小曲率半径和最大张力的影响因素进行分析。
3.1 软管最小曲率半径影响因素
在液货补给作业过程中,补给软管的曲率半径太小会引起软管挤压变形,不仅影响补给效率,还可能导致软管破损。因此,为了保证补给作业安全、高效进行,补给软管的曲率半径最小值应满足最小限值要求。由第2.3节分析可知,最小曲率半径发生在极值点位置,对式(10)求导取极值点,得x=xC,即最小曲率半径出现在最低点位置,最小曲率半径为

(13)
由式(13)可知,最小曲率半径由跨距l和参数β确定,由式(8)可知,当管长S确定时,β是跨距l和高差h的隐函数,因此,跨距l和高差h的改变都会影响最小曲率半径值。如图6所示,保持高差不变、改变跨距,最小曲率半径呈非线性快速增长趋势,因此,为保证液货补给作业的安全、高效,可通过增大跨距满足最小曲率半径要求。如图7所示,当跨距不变、高差改变时,曲率半径也呈增长趋势,但增长范围较小,高差变化6.0 m,曲率半径仅增加约0.5 m。

图6 不同跨距时的最小曲率半径
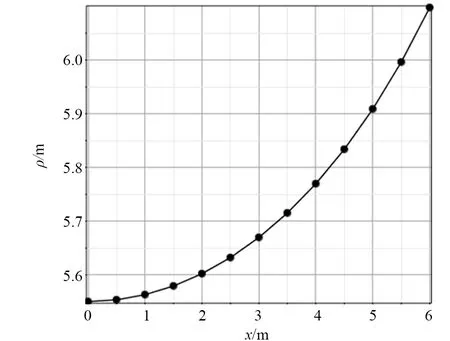
图7 不同高差时的最小曲率半径
3.2 软管最大张力影响因素
补给软管的张力太大,会直接导致软管断裂,严重危害补给作业的安全,补给软管的张力最大值应满足承载力限值。由第2.4节可知,软管的最大张力发生在补给软管较高端的端部位置,即当x=l时,

(14)
由式(14)和式(8)可知,在管长S确定的情况下,最大张力主要受高差h和跨距l的影响。由图8可知,当高差不变时,补给软管最大张力随跨距的增大呈非线性快速增长趋势,越接近管长增速越快,因此应避免软管的跨距接近管长,使软管保持一定的垂度。由图9可知,在保持跨距不变的情况下,补给软管张力最大值随高差的增大呈逐渐减小趋势,但高差对张力最大值的影响范围很小,因此,当高差变化范围较小时,可近似认为张力最大值恒定。
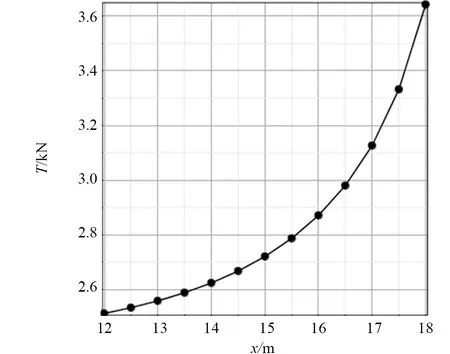
图8 不同跨距时的最大张力
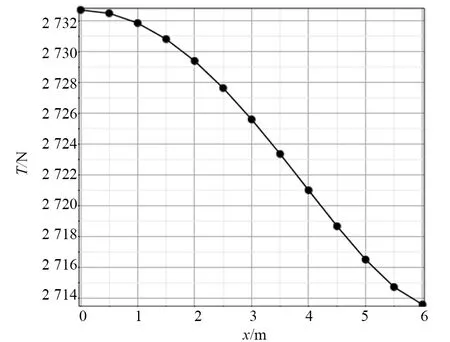
图9 不同高差时的最大张力
4 结 语
基于悬链线理论建立横向液货补给系统软管的静力学模型,分析得到补给作业过程中软管的线型函数表达式,通过数值分析得到补给软管的挠度曲线、曲率半径变化曲线和张力分布曲线。
分析曲线可知:补给软管的线型最低点和最大挠度点在管端不齐高的情况下不重合;补给软管的最小曲率半径发生在最低点位置,最大张力发生在软管较高端的端部位置。同时,通过分析补给软管最小曲率半径和最大张力的影响因素发现,跨距变化对最小曲率半径和最大张力的影响较大,高差变化的影响范围较小,因此通过改变跨距的方法调整软管曲线在现实操作过程中是切实有效的。
