核心问题引领思维走向深处

江苏无锡市育红小学 杨文君

江苏无锡市滨湖区教育研究发展中心 顾晓东

学生知识的积累、能力的形成、思维的发展离不开问题的引导。但当下小学数学课堂上，很多教师往往把提问设计研究的重点放在提问的技巧性上，过多地在问题的指向性和精确性上做文章，把提问的功能定位为“牵引”，所提问题往往是“花较短时间的即时浅层思考问题”，问题杂、细、碎的现象比较突出，不利于培养学生的深度思维习惯和能力。一节课时间有限，教师必须摒弃无效的，使学生思维活动处于不自主的、低下状态的伪问题，精心设计能凸显教学重点、搅动学生思维的，具有统领意义、涵盖面广、辐射性强的核心问题，并以此支撑课堂教学，引领学生思维走向深处。

教师在设计核心问题前，要精心研读教材，全面把握教材的横向、纵向联系，罗列整节课的相关问题，进行梳理和分析，理清核心任务，把握关键，整合提炼，从而确定核心问题。笔者结合不同类型学习内容的教学，初步归纳形成了一些核心问题类型及实践策略，结合实例做如下论述。

一、善问“是什么”：围绕释义型核心问题理解概念本质

概念是构成小学数学基础知识的重要内容。数学概念形式化外衣呈现出的是一种“冰冷的美丽”，而其实每一个数学概念都蕴含着人类在探索过程中的“火热思考”。有些概念教学课上由于知识点很多，容易出现一问一答式教学，看上去学生一直在回答问题，实则学习目标缺乏挑战性，学生思维缺乏深度和主动性。教师应在教学中引导学生经历概念产生和发展的过程，用核心问题把学生思维带回数学思考的原点，主动参与探究认知活动，在“火热的思考”中感悟和把握数学概念的本质特征。这就需要教师仔细梳理本课知识点，弄清本课学习重点、难点和关键，在此基础上精心筛选，围绕概念本质“是什么”提出释义型核心问题，引导学生主动探索知识，理解数学概念。

在《圆的认识》一课中，教材通过安排比、折、画、量等活动让学生会用圆规画圆，建立圆心、半径和直径的概念，理解圆的特征。虽然学生不能准确描述出圆的概念，但对圆形物体有充分的感知，一年级时也已初步认识圆。教学时，教师可以先让学生思考“圆与以往学过的平面图形有什么不同”，明确圆是平面上的曲线图形。在尝试画圆的基础上讨论“怎样用圆规把圆画好”。

生1：圆规的尖脚不能移动（定点）。

生2：要捏着上面部分转动，不能移动另一只脚（两脚距离要固定即定长）。

生3：转一圈时需要适当倾斜（旋转一周，同时介绍了技巧）。

学生们尝试和探索画法要点的同时，深刻地体会到“到定点的距离相等”这一本质。最后教师提出更进一步的问题：你准备怎样来介绍你画出的圆呢？学生们先愣了下，接着有学生轻声说：我画的圆比较小。有学生受到启发说：我画圆时把两脚拉开2厘米。在核心问题的引领下，学生们预习数学书第86页内容并交流。

生1：我画了一个半径2厘米的圆。

生2：我画圆时圆规两脚间距离是1.5厘米，所以圆直径是3厘米。

生3：我画的圆直径是4厘米。

还有学生主动要求到展台上介绍自己所画圆的圆心、半径、直径等。虽然学生没有准确地用文字表达出半径、直径的概念，但从他们的介绍中能看出已理解并会加以简单运用。在此基础上，教师再帮助学生完善直径、半径等概念。

教学这一课时，教师常会觉得要解决很多问题，要么问题过细过碎，学生思维层次水平较低；要么教师指定自学，学生缺乏学习主动性。教师可以将一些指向明确、缺乏探索空间的“小问题”浓缩和提炼，围绕“是什么”这一释义型核心问题，设计问题串：怎样用圆规把圆画好、介绍你画出的圆。在核心问题引领下，聚焦重点，明确目标，自觉自主思考，通过连续完整的学习活动，实现知识的深层加工及深刻理解，使学生的学习走向深处。

二、多问“为什么”：依托探理型核心问题推动数学思考

发展学生数学思考能力是数学教学的重要目标，必须在各种领域内容教学中加以落实。以计算教学为例，这在小学数学教学中占有很大的比重，主要围绕“理解算理”“建构算法”两个主要任务展开。在计算教学中，多数学生课前就有计算体验，对算法有一定的了解，尤其到了小学高年级，学生往往满足于掌握算法，但对算理不怎么了解。小学计算教学中要突破浅层次的操作和讲述，要借助已有经验实现类比迁移、贯通结构、建构算法，在此过程中充分突出算理对运算能力形成的重要性，做到“循理入法、以理驭法”，推动数学思考向深处进行。因而教师要思考、梳理学生常见方法背后蕴含的算理是什么，通过“怎样算”“为什么这样算”的探理型核心问题，激发学生数学思考，促进教学走向深处。

在教学《小数乘小数》一课，由于学生已有了将小数乘法转化成整数乘法进行计算的初步经验，教学时，先让学生估一估3.8×3.2的积，然后尝试计算，结果呈现两种竖式。

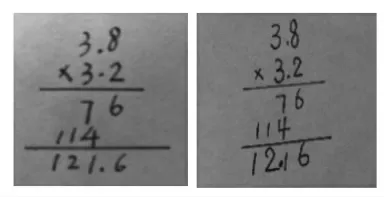
接着让学生观察两个算式并思考：这两种方法有什么相同和不同？你赞同哪种？为什么？在比较两个算式的异同时，学生很快理清都是转化成整数乘法计算，继而把关注点放到积的小数点应点在哪里。通过“赞同哪种？为什么？”这一核心问题，学生深入思考、充分交流对话、积极表达，展示自己的思维过程。

生1：我觉得第一种方法是考虑到小数点要对齐。

生2：我赞同第二种算法，因为前面估算的结果大约是12，121.6太大了，所以12.16比较合理。

生3：一位小数乘一位小数，积是两位小数。

学生大多点头表示同意这一结论。

教师乘机追问：小数加减法的结果有这样的规律吗？为什么一位小数乘一位小数，积是两位小数？停顿了几秒后有学生指出：因为都是看成整数乘法计算，其实就是把两个乘数都乘10，积就乘了100，要想使积不变，就得除以100，所以是两位小数。

紧接着让学生独立计算1.15×3.2，进一步加深对计算方法的理解。学生又联系小数点移动规律确定积中小数点位置的方法。最后概括算法时又围绕“小数乘法的关键是什么”，让学生尝试用简练的语言概括。学生互相补充，提炼出“①按整数算；②共几位点几位。”

当前课堂教学研究倡导的深度学习是一种主动的、探究式的、有意义的学习过程。上述案例教学中提问“为什么”，其实是围绕教学目标，直接把目标转化为探理型核心问题。学生围绕核心问题，通过第一次交流碰撞，主动探索积中小数点位置的确定；通过转化及迁移积的变化规律，初步确认算法的合理性；最后又用个性化的理解概括出小数乘法的计算法则。虽然是寥寥十个字，学生实则已经抓住了小数乘小数计算方法的要领，在探索和归纳的过程中，经历了深入的数学思考。

三、巧问“怎么做”：借助寻法型核心问题感悟思维策略

《义务教育数学课程标准（2011年版）》提出“四能”目标，即要发展学生发现和提出问题、分析和解决问题的能力。解决问题的策略成为小学数学教学的新焦点，策略教学是发展数学思维的重要渠道。解决问题教学以学生已有知识和经验为基础,通过把实际问题转化成数学问题，以具有挑战性、探索性、针对性的问题情境激起学生的探究欲望，并通过寻法型核心问题来驱动学生主动、深入思考，充分参与探索方法的活动，进而对解决问题的思维过程与方法进行反省认知，逐渐上升成为策略，提升学生思维的深刻性、灵活性、独创性等品质，积淀数学思想方法。

在《解决问题的策略（一一列举）》第二课时教学时，学生已体会到列举策略在解决有关实际问题时的作用，初步感知运用列举策略解决问题的基本思考过程和方法，也积累了一点运用此策略解决问题的经验。教师结合情境出示需要解决的问题，在明确可以用列举策略解决问题后，提出：“你准备怎样找出所有的比赛呢？”学生各自列举，在交流中出现了各种不同的列举方式。

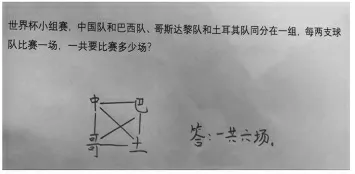
在交流完各种不同方法后，教师紧接着引导学生思考：这么多方法有没有共同之处？

生1：都是一一列举。

生2：都是按一定的顺序列举。

生3：都做到了不重复、不遗漏，找到所有的比赛。

上述教学过程围绕着“怎么做”这一核心问题，激起学生主动探索、表达，逐步培养学生的实践能力和反思意识。在后续的分析比较中，引导学生感悟列举方法的多样性，体会列举过程中合理使用列表、画图等辅助手段有助于不重复、不遗漏地列举，发展学生的有序思维，同时也让学生体会到数学知识和方法的内在联系，推动学生思维向深处发展。

核心问题是贯穿整节课或某个教学环节的关键问题，教学中应关注“是什么、怎么样、为什么”，使核心问题具有磁力，触及学生心灵深处，引发自主探究欲望；具有穿透力，能直指数学知识本质，紧扣数学思想方法；具有推动力，能引导学生持续建构，凸显知识结构体系。总之，教师应立足学生深度学习的需要，努力设计有新意、有深度的核心问题，以此提掣课堂学习，帮助学生深刻理解数学知识的本质，促进学生的深度学习，发展学生的高阶思维能力。