多维解读概念，探寻错例背后的原因——由求“运动场的周长”一题引发的思考

浙江宁波市奉化区松岙镇中心小学 汪 杰

概念教学是数学教学的一项重要内容，因此数学概念的掌握不只是简单的记住文本定义，而是要形成与概念直接联系的“整体性”的认知结构，包括相应的心智图像、对概念性质的辨认、对直观操作过程的识记、相应的范例重现等，这些就是被称之为数学概念的心理表征。其中“周长”是小学“图形与几何”领域的一个重要概念，笔者教学完“圆的认识”单元后，在周长的应用练习中发现了这样的问题。

一、错例描述

一个运动场（下图），两端是半圆形，中间是长方形。这个运动场的周长是多少？

在解决本题之前，学生已经会比较熟练地求一个圆的周长，而且本题的素材来源于学生的生活实际，对于六年级的学生来说并不难。然而反馈情况大出意外，学生普遍呈现了两种错例。

课后与其他年段的教师交流居然深有同感，虽然平时教学都很注重周长与面积的比较，如反复讲解两者的区别；讲解公式的含义；求同一个图形面积与周长练习；隔三岔五地解决问题，有一定的效果，但却不能彻底消除“病症”，而且达成一个共识：求组合图形周长的出错率明显高于求面积，“简单的周长”并没有想象中的简单。

二、概念解读

那么造成求组合图形周长困难的原因到底在哪里呢？笔者为此展开多个维度的周长概念解读，以期获得新的认识。

1.上位数学知识解读

在小学阶段，人教版数学对周长的定义是这样的：“封闭图形一周的长度，就是它的周长。”而在高等数学中比较精确的周长定义为：“环绕有限面积的区域边缘的长度积分，叫作周长。”两者定义中都包含了相同的要素“度量的对象——封闭图形的一周”“度量的结果——长度和”，但选用的描述用词却大不相同，两者相比我们可以发现：

其一，高数版定义中的“环绕”“边缘”两词很生动，形象地说明了从某一点出发，沿着周界回到起点，从而形成一条封闭的边线，其动态的过程便于学生描述，同时渗透判断一周的好办法——“跑一跑”；其二，“长度积分”比“长度”多了“积分”两字，凸显了周长不但需要度量长度，更要对度量结果进行累加。例如，三角形的周长就是围成三角形三条线段的长度总和，又如圆的周长其实是许多圆弧累加的长度总和；其三，“有限面积”与“封闭图形”两词虽然不同，但指明了周长与面积都依存于封闭图形中，有面积就一定有周长，两者相互依存，学习时人为割裂反而造成面积与周长概念互相混淆。

由此可见，从高位的视角来看待小学数学的概念定义，可以发现许多新的理解。

同时为了更好地抓住概念的本质，我们还可以从概念的特点来分析。通常在生活中我们都会碰到求篱笆总长等问题，这时需要一个固定的唯一的值来量化，这个具体的“数”就是周长。而这个“数”的获得，经历了“找一周”“度量”“求和”等一系列活动，具有清晰的“过程”性。因此，周长概念从“为了得到一个数表达周长”的结果需求出发，到经历“如何得到这个数”的操作过程，最终是“过程”和“结果”的共同体。

事实上，面积、体积等概念也具有“过程”与“结果”的两重特性，而周长作为“度量类”概念的起始学习内容，其过程性经验的积累就显得非常关键。

2.概念学习材料解读

在三年级周长概念形成阶段，教材提供了图1作为学生学习的材料，在概念的应用环节中又设计了图2作为巩固习题。

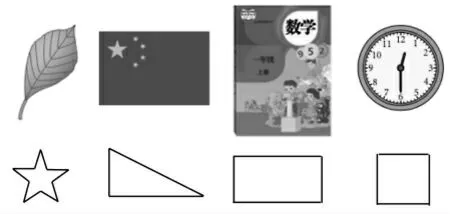
图1

做一做：

先量一量，再算出下面每个图形的周长各是多少。

图2

我们先来看图1的素材，涉及各种物体表面与平面图形，涵盖了直边、曲边与不规则的一周边线，为学生感知周长提供了丰富的活动材料。那为什么要呈现各种不同的物体表面呢？一方面教材清晰地表达了数学的知识来源于生活，学习周长需要基于学生的生活经验来展开；另一方面物体表面中有许多的干扰元素，如树叶内部有许多叶脉，钟面有数字、刻度，等等，学生在辨析“一周是什么”的过程中，逐步感悟到一周是一条“从起点回到起点的封闭边线”，这种过程性经验的积累，有助于学生形成“一周”清晰而又稳固的心智图像。

然而书本中的学材虽然丰富，但作为研究周长的典型正例却都不适宜。以教学中教师采用最多的树叶素材为例，其具有“一周边线”与“内线”的对比功能，但缺失的是感知“长度累加”的功效，因为学生既没有测量树叶边线的经验，也不具备准确测量的技能与方法，更遗憾的是没有测量长度的“真”需求。

再来看图2的巩固习题，三个图形的一周边线简单明了，学生无须“找一周”，凭借测量长度与计算求和就能获得周长，这样的过程性体验是不完整的，到后续求复杂组合图形的周长时，只懂“计算求和”，无视“一周在哪”的先天不足就会显现。

3.教材知识体系解读

为了更好地理清小学阶段周长概念的生长逻辑，笔者还整理出人教版数学有关周长知识体系表。

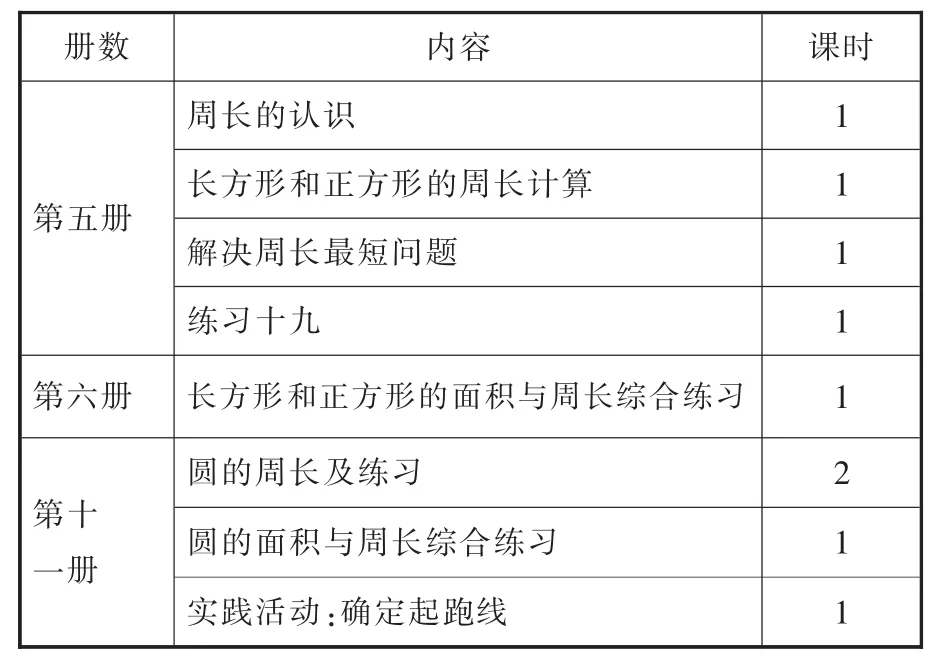
从整个体系来看，周长的概念形成阶段在三年级。首先让学生感悟到周长的研究对象和基本要素后，组织学生探究长正方形的周长，在概念应用中实现算法的优化，并建立公式模型；最后通过求图形拼组、分割后新图形的周长等综合性较强习题的操练，明晰面积与周长之间的区别，进一步凸显概念的本质。

周长概念的综合应用期在六年级，教材中设计了不少求圆周长与面积的生活实例，先让学生经历数学抽象的过程，再进行图形转化或直接运用公式解决问题。到这一阶段时，显然目标定位在数学抽象与策略优化。

比较尴尬的是四五年级，存在着一个较长时间的知识“断层期”，特别是在五年级研究多边形的面积时，整个单元注重的是面积公式的推导过程，教材既没有周长与面积公式的比较，也没有出现求组合图形周长的习题。由此经历一定量的练习后，学生自然看到组合图形就运用面积公式求值，而这种惯性思维对周长的过程性经验会产生强烈干扰。

三、归因分析

鉴于以上三个维度的概念再解读，我们不难找到错例的原因何在。

第一个错例的主因是学生对周长概念的意象不清。笔者课后与部分学生进行了访谈，学生们指着面积的区域说“一个圆的周长加上长方形的周长就可以了”，当笔者追问“那一周在哪里呢？”，学生才认识到自己错了。显然这部分学生对周长的核心要素“一周边线”“长度”心智图像模糊，导致与面积的概念表象互相干扰，对概念的辨别主要依靠观察文字描述，如看单位，找问题中的关键词“一周”“长多少”。

第二个错例的主因是学生求周长的过程性经验不足。“先找一周边线”→“测量累加求和”求周长的过程，在实际解决问题的过程中往往变成了应用公式求值的过程，这也侧面反映了我们教师在教学过程可能更注重周长值的获得，忽视了对于求周长过程性经验的整理回顾，由此学生头脑中形成的获得周长的过程记忆往往是零散的、片面的、不完整的。

综上所述，在概念教学之前，我们不妨先解读相关概念的上位数学知识，从而对其内涵有更加清晰的理解，更容易抓住本质；还可以仔细研究教材提供的学习材料，从其功能性、适切性等角度进行思辨，便于选材时扬长避短；也需要站在整个体系来看待概念的生长过程，进一步理清不同阶段所需达到的目标，由此进行适时的强化、比较、联结等，最终让概念实现稳固而又深刻的建构。