加速度计/磁强计组合弹道测量方法
2019-08-28祁克玉
孙 振,宁 波,祁克玉
(1.西安机电信息技术研究所,陕西 西安 710065;2.陆军装备部驻西安地区第四军代室,陕西 西安 710043)
0 引言
现有制导弹药技术中常见弹道测量方式有卫星定位、惯性测量。卫星定位系统能全天候提供高精度的三维位置、速度和精密时间信息。卫星定位系统是星基无线电导航系统,同无线电导航系统一样,容易受到干扰[1]。惯性测量因其高自主性、高隐蔽性的导航方式,无需从外界获取信号,即可实现导航参数的确定,不受其他工作条件的干扰和约束,因而在军用和民用领域都得到了广泛的应用,现代武器系统对惯导技术的需求越来越多[2]。
传统的惯性测量技术主要依靠加速度计测量线加速度,陀螺仪测量角速度。但陀螺抗过载能力差且高成本,不适合应用于榴弹等高动态特性的武器上。无陀螺惯性测量单元舍弃了陀螺仪,仅用抗过载能力强成本较低的加速度计实现测量功能。这种无陀螺系统非常适用于具有大动态角运动范围的载体。无陀螺惯性测量单元相比于有陀螺的系统具有相当多的优点:成本低、寿命长、高抗过载和快速启动。但传统的多加速度计组合惯性测量单元是利用比力解算得到角速度,利用对数法、开方法解算精度较低且存在奇异问题。利用比力解算出的角速度无论是采用欧拉角法、旋转矢量法还是四元数法解算出的姿态角都存在误差积累快、精度不高的问题[3]。目前二维弹道修正组件弹道测量中存在卫星定位法难抗干扰,惯导方法中陀螺抗过载低、不适用高转速,纯加速度计测量方法姿态测量误差大、有误差积累效应等问题,需要寻求抗过载能力强的弹上自主弹道测量的技术方法,以替代目前卫星和磁强计组合的测量方式。现针对高旋弹二维弹道修正组件提出了利用多加速度计/磁强计组合的全自主测量方法。
1 加速度计空间配置方案
由于要应用于高旋榴弹二维弹道修正组件平台,组件内部空间有限,尤其是轴向空间受限,因此采用扁平状的结构能节省轴向空间。选取常见的十二加速度计构型方案如图1所示。图中坐标系Oxyz是弹体坐标系,原点位于弹体质心,x轴为弹轴方向,y轴垂直弹轴向上,z轴根据右手定则确定,加速度计敏感方向如图1所示。

图1 加速度计空间配置图Fig.1 Accelerometer space configuration chart
图1中的1,2,…,12是单轴加速度计,箭头方向为敏感矢量方向。加速度计安装位置r和敏感矢量θ为:

(1)

(2)
在仅用加速度计来测量计算载体运动参数时,为了得到完整的线速度和角信息,不能将所有的加速度计都安装在质心位置,需要有部分安装在非质心位置。加速度计的数量、安装位置将决定该构型是否可行。
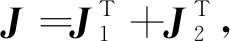
根据加速度计输出的比力f1~f12可以解算出弹体三轴角速度,
(3)
式(3)中,

(4)
利用加速度计比力解算可得到载体线加速度,结合初始位置可积分得到线速度和位置,同时可利用对数法、开方法等方法解算出角速度,再利用欧拉角法求解姿态即可得到载体三轴姿态角[3]。但此方法得到的姿态角信息误差较大,且随时间误差发散。利用BP神经网络等方法预测角速度虽误差相对收敛,但工程实现难度大,且算法复杂[4]。因此需要引入其他信息实现较准确的姿态测量。
2 多加速度计/磁强计组合惯性测量方法
针对上述问题,引入三轴磁传感器与加速度计系统组合进行弹道测量,利用加速度计来测量线加速度以解算线速度、位置及俯仰、偏航角度,利用磁强计测量滚转角,实现全自主高精度弹道测量。
2.1 线速度和位置解算方法
在无陀螺捷联惯导中,载体加速度计算公式为[5]:
(5)
(6)
以上计算出的加速度是弹体系下的,需要将其从弹体系转换到地面系,然后进行积分,可以得到地面坐标系下的载体速度和位置。
2.2 姿态角解算方法
常规的弹体姿态测量需要精确测量俯仰角、偏航角和滚转角。但二维弹道修正平台中滚转角的测量对系统修正精度影响最大,姿态解算重点是实现滚转角精确解算[5]。
对于高旋榴弹,其飞行稳定时的攻角、侧滑角非常小,可以忽略其扰动影响。假设速度方向与弹轴方向一致,姿态角可由弹轴方向确定变成速度方向确定,则弹丸的偏航角φ和俯仰角θ可由下式求得:
(7)
式(7)中,vx、vy和vz是地面系下的弹体三轴线速度,由加速度计比力解算后转换坐标系得到。
弹丸滚转角的解算原理是:在描述弹丸姿态运动时,地磁场矢量在各个坐标系下存在坐标转换,磁矢量在不同坐标系下转换的转换矩阵中存在姿态角参数,因此可以解算出姿态角。
1)发射坐标系OXlYlZl(L)
发射坐标系原点在炮口断面中心,OXl轴沿水平线指向射击方向,OYl轴沿铅直方向向上,OZl由右手法则确定。


以上三个坐标系与姿态角的关系如图2所示。
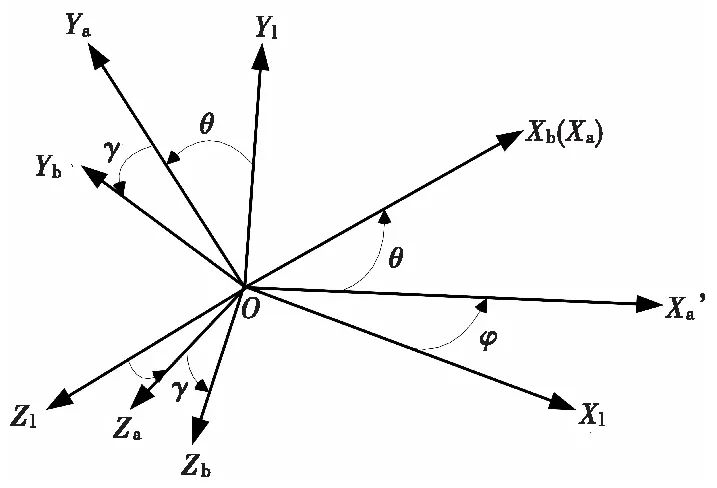
图2 坐标系与姿态角的关系Fig.2 Relation between coordinate system and attitude angle chart
设炮口断面中心处地磁矢量为H,磁偏角为D,磁倾角为I,射向角为ψ。地磁场矢量在弹体系和地面系之间的转换关系如下[5]:

(8)
由式(8)可知,坐标转换方程是线性相关方程,不能独立解出三个姿态角,只要得到三个姿态角中的一个姿态角信息,理论上可以解算出其余两个姿态角[6-7]。
地磁矢量在发射坐标系下坐标为:

(9)
根据式(9)可得到发射系下的地磁矢量。
展开式(8)解出sinγsinγ和cosγ,进而可得到滚转角解算公式为:
(10)
式(10)中,k1=(Xlsinφ+Zlcosφ),k2=(Xlcosφsinθ-Ylcosθ-Zlsinφsinθ)。
式(10)中的Yb和Zb由磁传感器测得,故可测得滚转角。但滚转角解算模型决定了需要对滚转角进行真值判定,即以下四种情况[8]:

加速度计/磁强计组合测量算法流程图如图3所示。

图3 无陀螺惯性测量单元算法流程图Fig.3 GFIMU algorithm flow chart
3 仿真验证
仿真目的:验证加速度计/磁强计组合测量精度是否达到卫星/磁强计组合测量精度水平,是否满足二维弹道修正组件制导需求(角度误差小于10°)。
利用122 mm榴弹的仿真弹道数据,分别进行三组方案的仿真:第一组仅利用多加速度计组合的方案,采用图1的方式;第二组利用卫星和磁强计组合的方案;第三组利用多加速度计/磁强计的组合方案。
装配加速度计测量样机,搭载122 mm榴弹二维弹道修正组件外场试验,得到实测加速度计比力数据和磁强计数据,利用实测数据进行仿真。样机如图4所示。

图4 加速度计/磁强计系统样机图Fig.4 Accelerometer/magnetometer system prototype diagram
仿真步骤如下:
1) 确定弹丸发射位置以及初始姿态角。
2) 确定炮口断面中心点磁矢量信息H、D、I。
3) 将122 mm榴弹二维弹道修正组件中加速度计输出作为系统仿真输入(第一组);将122 mm榴弹二维弹道修正组件中三轴磁强计和GPS实测数据作为系统仿真输入(第二组);将122 mm榴弹二维弹道修正组件中三轴磁强计和加速度计实测数据作为系统仿真输入(第三组);采样周期T=0.001 s,仿真时间64 s。
4) 将上一步比力结果代入式(6)得到加速度,数值积分得到弹丸速度和位置信息(第一、三组),卫星测量数据得到弹丸速度和位置信息(第二组)。
5) 将速度代入式(7)解算出弹丸俯仰角和偏航角。
6) 利用122 mm榴弹弹道修正组件中三轴磁强计数据和式(8)、式(9)、式(10)解算滚转角。
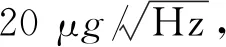
仿真结果如图5-图13所示。
仿真结果分析:对比图5-图7与图9、图11、图13,加速度计/磁强计组合测量精度误差在5°以内,且不发散,相比于仅用加速度计的系统测量精度大幅提高,且满足了二维弹道修正组件的制导精度要求。对比图9、图11、图13与图8、图10、图12加速度计/磁强计组合与卫星/磁强计组合姿态角测量误差均在5°以内,均可满足二维弹道修正组件制导需求。对二维修正组件修正影响最大的姿态角是滚转角,加速度计/磁强计组合滚转角误差最大值和方差均小于卫星/磁强计系统,因此在二维弹道修正组件中加速度计/磁强计组合可替代卫星/磁强计组合实现全自主弹道与姿态测量,且测量结果更精准。

图5 多加速度计组合俯仰角误差Fig.5 Pitch error of multi-accelerom eter system

图6 多加速度计组合偏航角误差Fig.6 Yaw angle error of multi-acceler ometer system

图7 多加速度计组合滚转角误差Fig.7 Roll angle error of multi-accelero meter system
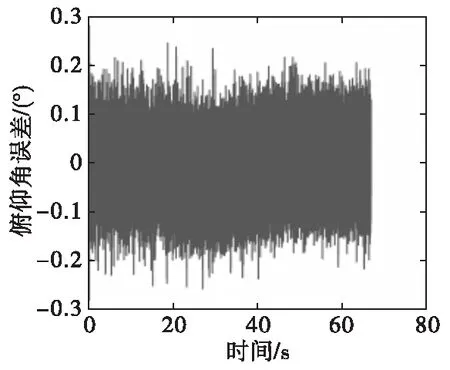
图8 GPS/磁强计组合俯仰角误差Fig.8 Pitch error of GPS/magnetometer system
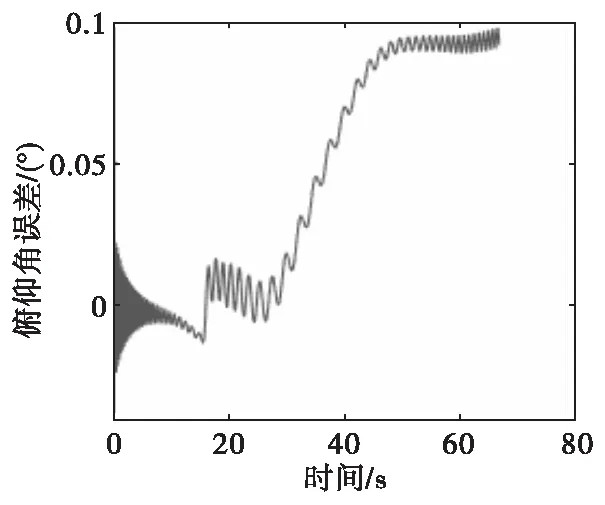
图9 加速度计/磁强计组合俯仰角误差Fig.9 Pitch error of accelerometer/magnetometer system

图10 GPS/磁强计组合偏航角误差Fig.10 Yaw angle error of GPS/magnetometer system

图11 加速度计/磁强计组合偏航角误差Fig.11 Yaw angle error of accelerometer/magnetometer system
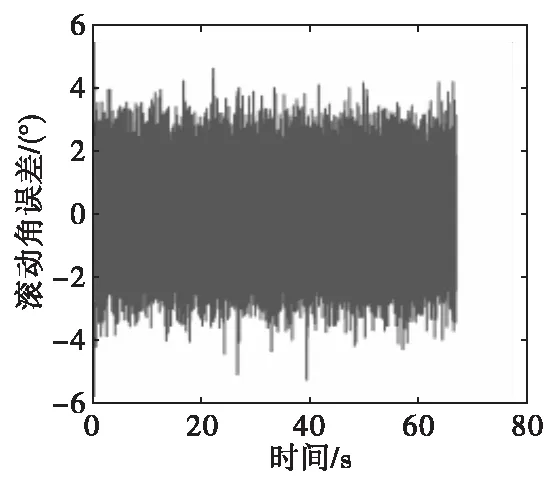
图12 GPS/磁强计组合滚转角误差Fig.12 Roll angle error of GPS/magnetometer system

图13 加速度计/磁强计组合滚转角误差Fig.13 Roll angle error of accelerometer/ magnetometer system
4 结论
本文提出了加速度计/磁强计组合的全自主弹道测量方法,建立了弹道测量仿真模型,验证了算法的可行性和准确性。该方法不依赖卫星等第三方设备,仅用加速度计/磁强计即可完成弹道测量,测量精度比纯加速度计组合系统测量精度高,且误差随时间发散程度低,理论上完成了较高精度的全自主弹道测量。制作了加速度计比力和磁强计数据采集样机,利用外场试验采集了比力、磁强计数据源进行仿真验证。仿真验证结果表明,加速度计/磁强计测量系统在不借助卫星定位的前提下能获得与有卫星测量系统同水平的精度,可满足二维弹道修正组件制导需求,有进一步的研究价值。
