多退化变量灰色预测模型的滚动轴承剩余寿命预测
2019-08-28张雨琦邹金慧
张雨琦,邹金慧,马 军
(1.昆明理工大学信息工程与自动化学院,云南 昆明 650500;2.云南省矿物管道输送工程技术研究中心,云南 昆明 650500;3.昆明理工大学机电工程学院,云南 昆明 650500)
滚动轴承是旋转机械中用途最为广泛的零部件,其剩余寿命的长短与设备运行安全、运行工况间存在着直接关联,由其引发的故障是造成设备失效的重要原因。因此,对滚动轴承剩余寿命进行预测对于预防设备失效和实现基于状态的设备维护具有重要意义。
目前,剩余寿命预测的方法主要可以分为机理建模和数据驱动建模两种类型[1]。机理建模的方法主要是指根据设备的内在运转机理及工作原理来建立设备的退化模型从而对剩余寿命进行预测[2-3];数据驱动建模的方法主要是指通过数据拟合的方式对能反映设备退化性能的主要性能变量进行拟合,并根据其变化趋势来预测设备的剩余寿命。考虑到滚动轴承的机理具有一定的复杂性,而据此构建机理模型较为困难,因此以数据驱动为支撑的方法在剩余寿命预测中应用较为广泛。文献[4]以最小量化误差为衰退指标,利用自组织映射神经网络对轴承剩余寿命进行预测。文献[5]选择改进的EMD以全寿命周期振动信号为对象进行分解,并将不同阶段的退化特征量输入灰色模型进行训练并对轴承剩余寿命作出预测。文献[6]选择飞机空气制冷机作为研究对象,应用谱峭度和最小二乘支持向量机的方法对其寿命趋势进行预测。
然而,这些模型都存在一定缺陷,只考虑了一个特征参数或单独分析了几个特征值的状况和趋势,并没有将相关的特征值作整体以及系统性的把握。本文针对此问题,提出了多退化变量灰色预测模型的滚动轴承剩余寿命预测方法。
1 多退化变量灰色预测模型与CUSUM算法理论
1.1 多退化变量灰色预测模型
灰色系统理论是探究某些既存在已知信息,同时也存在未知或无法确知信息的理论和方法。以此理论为基础,可以在离散、有限与杂乱的数据中梳理出规律,并构建相应的灰色模型,对数据的趋势与发展状况进行探究。在灰色预测分析中,最经典的模型是单一变量灰色预测模型,即通过一个变量的一阶微分方程揭示序列的变化趋势。但对于复杂工况下的预测,需同时跟踪多个特征参数的影响,并对他们进行融合。因此引入多退化变量灰色预测模型来根据多个变量的变化趋势对轴承寿命进行预测[7-8]。

(1)
式(1)中,i=1,2,…,n;k=1,2,…,m,m为每个序列的数据个数。

dX(1)/dt=AX(1)+B
(2)

记ai=(ai1,ai2,…,ain,bi)T,i=1,2,…,n,则:
(3)
式(3)中,L=(L1,L2,…,Lj,…Ln,1),
则多变量灰色预测模型的计算值为:

(4)
(5)

(6)
当n=1时,多退化变量灰色预测模型退化为单一变量灰色预测模型。
1.2 CUSUM算法理论
在实际工程中,当滚动轴承开始工作后,随着时间的增加,其状态会由正常逐渐发生退化,对于滚动轴承的剩余寿命预测而言,如果从滚动轴承起始正常无故障运转状态进行剩余寿命预测,则会出现较大误差,因此需要对早期故障点即突变点进行识别,从突变点开始进行剩余寿命预测会更为合理。基于此,引入CUSUM算法对突变点进行判断。
CUSUM算法是通过对事件的突变状态进行累积,将过程中的小偏移量累加起来,求其累积和进而判断是否发生突变。该算法要求的假定条件较少,能有效反映过程变化的灵敏性,非常适合用于滚动轴承寿命退化过程中的突变检测。其算法步骤如下所示[9]:

(7)
步骤2 令累积和Ti为:
(8)
式(8)中,i=1,2,…,n。
步骤3 找出Ti中的最大值Tmax,其对应的点的横坐标xmax就是早期故障点即突变发生时刻:
|Tmax|=max(|Ti|)
(9)
2 多退化变量灰色预测模型的滚动轴承剩余寿命预测方法实现步骤
由于单一退化变量灰色预测模型缺乏对能够表征滚动轴承退化过程的其他变量的分析考量,可能导致有效的信息丢失,使得预测的准确性与精度受到一定的限制,因此本文以对滚动轴承性能退化过程敏感的多个特征参数为基础,建立多退化变量灰色预测模型对滚动轴承剩余寿命进行预测。其预测流程如下:
1) 选取滚动轴承全寿命周期数据并提取对其退化趋势敏感的均方根、峭度、功率谱密度均值三个指标。
2) 将1)所述的三个指标分别输入多变量灰色预测模型进行预测,通过各种误差精度来计算指标权重,并根据CUSUM累积和理论判断出早期故障文件。
3) 从早期故障文件开始,选取相同间隔工作时间文件的三个特征值输入多退化变量灰色预测模型中进行训练并得到辨识参数值。
4) 结合辨识参数值对训练指标进行拟合并预测下一时刻的退化性能指标。
5) 通过多退化变量灰色预测模型建立退化性能指标与寿命之间的非线性映射关系,并对下一时刻的滚动轴承剩余寿命进行预测。
算法流程图如图1所示。

图1 滚动轴承剩余寿命预测流程图Fig.1 Flowchart of theresidual life prediction in rolling bearing
3 实验验证
3.1 实验平台介绍
笔者采用美国辛辛那提大学智能维护系统的滚动轴承全寿命周期数据进行实验[10]。图2展示了其实验平台状况,主轴上装配4个Rexnord ZA-2115双排列轴承,主轴由直流电机以皮带为媒介提供动力,每个轴承每排包含16个滚动体,所有轴承均采用油润滑,转速为2 000 r/min,通过弹性系统向轴和轴承上施加6 000 lb(2 721.5 kg)的径向载荷,借助NI DAQ 6062 E数据采集卡采集数据,所有数据均为加速疲劳实验。本文选取的数据集采样频率为20 kHz,数据采集间隔时间为10 min,采集数据次数为984次,在每组数据中,采样点的数量为20 480个,在实验的末尾,轴承1在持续运转约163.83 h时,出现了失效问题,具体表现为外圈损伤严重,图3描述了其从正常运转到外圈故障失效的全寿命过程时域波形图。

图2 轴承全寿命周期数据实验平台Fig.2 Experimental platform for lifetime data of rolling bearing
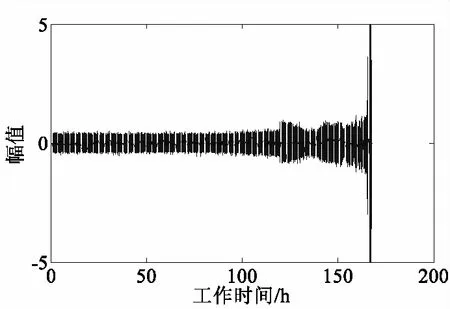
图3 轴承全寿命周期数据时域波形图Fig.3 Time domain waveform diagram of lifetime data
3.2 指标选取依据
滚动轴承在运作过程中局部出现故障时,其振动信号中不仅包含故障引起的瞬态冲击信息,还存在轴转频、倍频等谐波成分和噪声,以致其振动信号的能量和波形产生一定的变化。基于此,在训练样本的选择上,不能直接以振动信号的振幅特征为准。在实践操作中,主要的统计特征包括峰值、绝对平均值、均方根、波形系数、峰态因子、脉冲因子、裕度因子、偏度、峭度、功率谱密度均值等。结合现场实践状况[11-14],本文选取RMS(均方根值)、峭度、功率谱密度均值三个特征来描述滚动轴承整个寿命周期的变化趋势:
1) 均方根值:即有效值,由于均方根值是对时间的平均,所以对存在表面裂纹且表现出无规则振动波形的故障表现出较显著的敏感特性,针对故障测量值可做出恰当的评价[15],描述为:
(10)
2) 峭度:峭度是反映波形尖峰度的归一化累积量。当滚动轴承在无故障条件下运行时,其所表现出的振动信号幅值基本是符合正态分布规律的,峭度指标值K≈3。当滚动轴承局部表现出故障时,因故障带来的冲击,振动信号概率密度会呈现出显著异常的增加,信号幅值分布不会再贴合正态分布,相应的峭度值会显著增大,由此可以将其作为有效反映轴承是否存在故障的指标[16]。
峭度指标可表示为:
(11)
3) 功率谱密度均值:以功率谱变化(是否有额外谱峰)为依据,可以对故障是否存在作出科学判定。而功率谱密度均值则是对每段数据作采集,并依次完成功率谱密度求解,累加平均之后,其结果即定义为功率谱密度均值[17]。
将自相关函数Rx(τ)的傅里叶变换通过下式作具体描述:
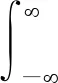
(12)
Sx(f)即为x(t)的功率谱密度函数。则其均值为:
(13)
式(13)中,n=1,2,…,n表示数据分段数。
分别选取上述三个指标:均方根值、峭度值、功率谱密度均值,并计算采集的每组数据的三个指标量化到区间[0,1]的归一化值(共984组数据文件)绘制出如图4—图6所示的描述全寿命周期数据变化趋势的各个特征图。当轴承表面刚开始出现故障时,形成小的剥落或裂纹,均方根、峭度和功率谱密度均值随之逐渐变大,之后由于连续的滚动接触,三个指标均经历一段平滑阶段,当损伤扩展到更大范围时,冲击再次变大,三个指标持续攀升且攀升幅度明显增大,此时轴承出现严重故障并使机械设备无法继续运转[10,18]。由图3—图6均可知,轴承前期并没出现故障,如果根据整体周期数据进行预测并不合理,因此需要对最早出现故障的文件标号数进行判断。

图4 均方根特征归一化趋势图Fig.4 Normalization trend of root mean square

图5 峭度特征归一化趋势图Fig.5 Normalization trend of kurtosis

图6 功率谱密度均值特征归一化趋势图Fig.6 Normalization trend of mean power spectral density
3.3 滚动轴承早期故障识别
由于上述三个敏感指标对滚动轴承寿命数据退化情况的表征不同,依据均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方百分比误差(MSPE)、均方根误差(RMSE)这五种误差来计算不同特征值所占权重[19],分别将三个特征值输入多退化变量灰色预测模型之中,并根据权重占比来综合判断其最早出现故障的文件。
(14)
(15)
(16)
(17)
(18)
式(14)—式(18)中,Q0代表原始值,Qm代表预测值,N为样本组数。

(19)
式(19)中,i为第i个特征,N代表特征总数,本文取N=3。
由上式分别计算出峭度、均方根值、功率谱密度均值在综合指标中所占权重,如表1所示。根据不同特征的权重计算出综合指标并绘制出如图7所示的经平滑处理(Moving Average, MA)后的归一化综合指标退化趋势图,平滑处理如式(20)所示。

(20)
式(20)中,Ns表示去掉均值后的数据总数,s表示存在于子矩阵中的数据数,一般情况下为奇数且s≪
Ns,dn表示原始综合指标中的第n个指标值,man为经MA处理后的新指标值。

表1 三个特征在综合指标中所占权重表
由文献[20—22]可知,故障均发生于400号文件以后,计算出前400号文件的综合指标均值,如图7中直线所示。根据综合指标线与均值线相交部分的放大图可知,突变文件大概位于400—600号文件中间,根据1.2节介绍的CUSUM算法,以600号文件为界,绘制出累积和曲线图如图8所示,可知当文件标号为532号时,曲线发生突变。
结合图9绘制出的532号文件前后文件的包络谱变化图,可以更清楚地显示出532号文件处故障还未明显发生,在533号文件处出现早期故障,在534号文件时故障表示明显,由此可以判定轴承从533号文件开始发生故障,即533号文件为早期故障点(对应时间是:轴承已经工作88.67 h时)。

图7 归一化综合指标退化趋势图(经平滑处理)Fig.7 Degradation trend of normalized comprehensive index (smoothed)

图8 累积和曲线图Fig.8 Cumulative sum curve

图9 文件包络谱Fig.9 Envelope spectrum
3.4 滚动轴承剩余寿命预测
由于已判断出全寿命周期数据是从533号文件开始发生故障,则根据故障发生规律和图10所示,分别从早期故障点533号文件和第一次出现明显故障表示(即第一个波形尖端)的704号文件进行寿命预测。从533号文件开始,每隔20个文件取一次数据,共取16组数据的三个退化变量值作为训练样本,并将其输入多退化变量灰色预测模型,分别获取预测辨识参数,预测之后7组数据的寿命值。从704号文件开始,每隔20个文件取一次数据,共取9组数据的三个退化变量值作为训练样本,同样以上述方法预测后6组的寿命值。预测结果分别如图11、图12所示,由图可知,从早期故障点开始进行预测,其特征值经历了整体的故障变化趋势,预测结果与实际寿命值误差不大,而从明显出现故障表示的故障点开始预测,由于其在初期的故障后,经历一段时间的平稳过渡阶段再进入深度故障期(即特征值出现下降再上升的过程),则预测的后期会出现较大误差,因此本文取早期故障点的特征值为初始特征输入多退化变量灰色预测模型中进行剩余寿命的预测。

图10 寿命预测故障点提取图Fig.10 Fault point extraction for life prediction
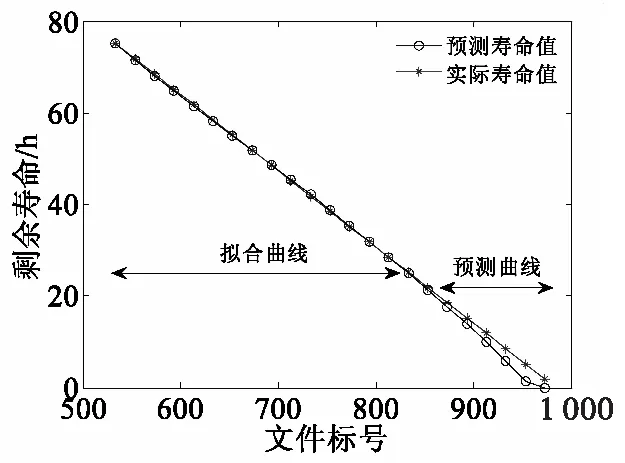
图11 多退化变量灰色预测模型寿命预测对比图(533号文件起)Fig.11 Life prediction comparison diagram of grey prediction model with multiple degenerate variables (from No.533)

图12 多变量灰色预测模型寿命预测对比图(704号文件起)Fig.12 Life prediction comparison diagram of grey prediction model with multiple degenerate variables (from No.704)
3.5 不同预测模型误差精度对比
为了对比和评估预测结果,将灰色预测模型(多退化变量与单一变量)、SVR(支持向量回归)预测模型、BP神经网络预测模型的分析结果作进一步对比,对比图如图11、图13、图14、图15、图16所示(由于预测已工作时间可能出现超过实际寿命值的情况,因此对于剩余寿命为负值的情况全部设置剩余寿命为0),其中图14为图13预测曲线部分(即虚线部分)的局部放大图。分别计算出各预测寿命曲线与实际寿命曲线相应的MSE,MAE,MAPE,MSPE,RMSE与NSE,将它们作为评价模型优劣的指标。其中NSE指纳什系数,该系数是用来反映模型质量的参数值,若纳什系数越接近于1,则证明模型质量越优[23],纳什系数表示为:

图13 单一变量灰色预测与多变量灰色预测对比图(533号文件起)Fig.13 Comparison diagram between grey prediction with single variable and multiple variables(from No.533)

图14 单一变量灰色预测与多变量灰色预测对比局部放大图Fig.14 Local enlarged diagram of comparison between grey prediction with single variable and multiple variables
(21)
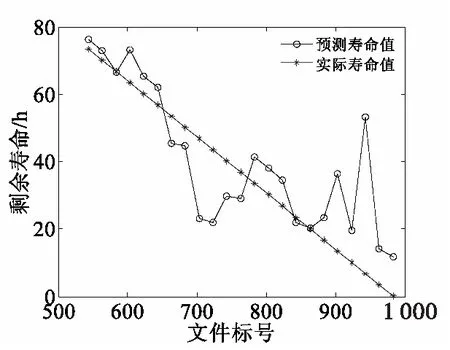
图15 BP神经网络预测模型寿命预测对比图(533号文件起)Fig.15 Comparison diagram of BP neural network model for life prediction(from No.533)
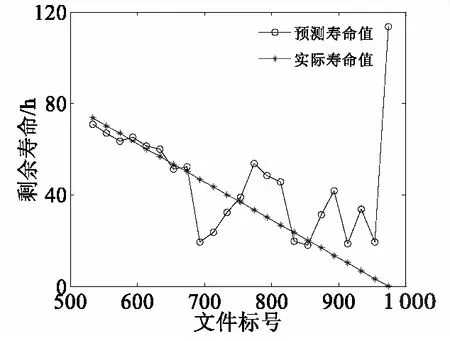
图16 支持向量回归预测模型寿命预测对比图(533号文件起)Fig.16 Comparison diagram of SVR model for life prediction(from No.533)

图17 多退化变量灰色预测曲线95%置信区间图Fig.17 95% confidence interval diagram of grey

图18 BP神经网络预测曲线95%置信区间图Fig.18 95% confidence interval diagram of BP

图19 SVR预测曲线95%置信区间图Fig.19 95% confidence interval diagram of SVR prediction curve with multiple degenerate variables neural network prediction curve prediction curve

预测数据组数1234567实际已使用寿命/h142.000 0145.333 3148.666 7152.000 0155.333 3158.666 7162.000 0单一变量灰色预测(峭度)预测已使用寿命/h140.994 4143.846 0146.605 6149.269 3151.833 2154.294 4156.650 4相对误差/%0.7081.0231.3861.7972.2532.7563.302单一变量灰色预测(均方根)预测已使用寿命/h140.903 1143.689 1146.368 0148.935 5151.388 2153.723 2155.938 6相对误差/%0.7721.1311.5462.0162.5393.1163.742单一变量灰色预测(功率谱密度均值)预测已使用寿命/h138.974 8141.231 9143.352 7145.339 4147.195 3148.923 9150.529 3相对误差/%2.1302.8223.5744.3825.2396.1407.081多变量灰色预测预测已使用寿命/h142.471 3146.143 2149.932 8153.886 8158.063 4162.532 3163.83 相对误差/%0.3310.5570.8511.2411.7572.4361.129

表3 三种模型寿命预测值与实际寿命值误差对比表
图17—图19分别展示了三种预测模型预测结果曲线的95%置信区间。由图中可知,虽然三种模型的预测结果均处于95%置信区间内,但BP神经网络预测模型和SVR预测模型所预测出的结果表现出较大的离散性,而多退化变量灰色预测模型则呈现出较高的精度。单一变量灰色预测模型与多变量灰色预测模型的相对误差如表2所示。三种预测模型和灰色预测模型中的多退化变量预测与单一退化变量预测对比的各种误差评价指标计算结果如表3所示。从表2、表3中可以看出多退化变量灰色预测模型预测结果能更好地逼近真实寿命值,各种误差均优于单一变量灰色预测和其他两种预测模型,而能表征模型质量的参数纳什系数则高于其他两种预测模型。因此,结合了多个退化变量的灰色预测在小样本条件下预测轴承寿命更优于单一变量灰色预测,而灰色预测模型,则要优于SVR预测模型与BP神经网络预测模型两类模型。
4 结论
本文提出了多退化变量灰色预测模型的滚动轴承剩余寿命预测方法。该方法结合多个表征轴承退化趋势的特征参数与早期故障突变点对滚动轴承进行早期故障识别,并利用轴承寿命与特征参数之间的映射关系建立多退化变量灰色预测模型对滚动轴承剩余寿命进行预测。仿真实验结果表明,本文所提取的参数集能够有效表征滚动轴承退化趋势,多退化变量灰色预测模型的预测精度及可靠性均优于单一退化变量灰色预测模型、BP神经网络预测模型及SVR预测模型,对滚动轴承的剩余寿命研究具有重要的指导意义。
