弹性体导弹自适应减振跟踪控制算法

何阳光,李小兵,赵思源,熊思宇

(空军工程大学防空反导学院,陕西 西安 710051)

0 引言

在现代战争中,高性能的导弹对战争的胜负起着十分重要的作用,因此,提高导弹的飞行速度、射程与机动性等性能越来越迫切。为了提高导弹的速度与机动性,导弹的外形便趋于细长化设计。通常把长径比大于15的导弹称为大长径比导弹或弹性体导弹,大长径比导弹相比于过去的导弹,由于弹性特征十分明显,除了要解决参数摄动、干扰和不确定性等问题,还要考虑弹性振动的抑制。否则有可能会影响弹上设备的正常工作,甚至造成损坏。

解决不确定性问题,尤其是非匹配不确定性问题,常用的方法为反演控制[1],但单纯的反演控制存在“计算爆炸”问题,比较好的解决办法是引入一阶低通滤波器,即动态面控制[2]。除了反演控制以外,滑模控制方法对匹配不确定性具有很强的鲁棒性[3],因此,可以将两者结合,获得更好的控制效果。随着干扰观测器的提出,利用干扰观测器来估计系统中的干扰和不确定性成为解决非线性系统控制问题的一个新方法[4]。针对振动抑制问题,采用常规的鲁棒控制类方法仅能保证系统的稳定性,并不能实现振动的有效抑制[5],弹上设备依然处于恶劣的工作环境中。为了解决这个问题,学者们作了大量研究,Sahjendra[6]针对模型未知的弹性飞行器的大角度机动问题设计了自适应控制器,并引入模态速度反馈补偿器抑制弹性振动,取得了较好的控制效果。此外,Zhen Yu[7]和Rickey[8]等分别采用自适应位置反馈和模型预测的方法实现振动的抑制,但以上文献中均将刚体运动与弹性振动分离,使用了作动器产生横向控制力来抑制振动,这样将会增加硬件结构的复杂性。张雷[9]等人采用两自由度H控制方法,把振动模态引入到性能函数中,达到振动的主动抑制,但没有考虑弹性振动对刚体运动的影响,所设计的控制器较复杂,且对模型精度有一定要求。Wu Guanghui[10]对弹性高超声速飞行器设计了基于非线性干扰观测器的鲁棒自适应反演控制器,加快了振动的衰减速度。采用类似方法的还有Wang Na[11],他们都是将弹性模态视为干扰,利用观测器估计出弹性模态的值,但所用的弹性高超声速飞行器模型中弹性振动改变的是模型的参数进而影响系统状态的变化率,并没有直接改变系统状态的大小,因此,刚体运动与弹性模态的耦合程度低,当弹性振动直接改变系统状态的大小时,弹性模态的抑制效果一般。Ahmad[12]设计了基于神经网络的主动振动抑制器,利用神经网络强大的非线性逼近能力克服弹性振动。本文针对受非匹配不确定影响的弹性体导弹弹性振动与刚体运动耦合问题,提出一种基于非线性干扰观测器的自适应反演控制算法。

1 模型描述

1.1 刚体运动模型

大气层内导弹俯仰/偏航通道非线性刚体模型为[13]:

(1)

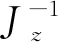
1.2 弹性振动模型

在建立弹体弹性振动模型之前,先给出弹性坐标系的定义:坐标系的原点O选择在弹头顶点上,Ox轴与刚体弹轴重合,由弹头指向弹尾,Oy轴在俯仰平面内,与Ox轴垂直并指向上方,Oz轴与Ox轴和Oy轴垂直,并形成右手直角坐标系。将导弹视为两端自由的欧拉梁,以俯仰通道为例,弹体横向振动的方程为：

(2)

式(2)中,y(x,t)为表征梁弹性变形的函数,m(x)为质量分布函数,EI(x)为刚度分布函数,Wy(x,t)为梁受到的侧向力,边界条件为：

此边界条件表示梁两端的弯矩和剪力都为零。

弹性变形函数y(x,t)的表达式为：

(3)

式(3)中,qi(t)为第i阶振型的广义坐标,Φi(x)为第i阶模态振型函数,将式(3)代入式(2),采用分离变量法得到如下广义坐标方程：

(4)

式(4)中,ξi、ωi分别表示第i阶振型的阻尼比和固有振动频率,Qi为第i阶振型的广义力,Mi为第i阶振型的广义质量,且有：

(5)

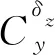
Φi(x)=ai(sinhkix+sinkix)+coshkix+coskix,

弹性变形会引起俯仰角发生变化,产生一个附加的角速度,由弹性振动产生的附加俯仰角速度为：

(6)

偏航通道振动模型与俯仰通道类似,为简化计算,本文仅考虑前两阶弹性振动模态,结合式(4)和式(6),下面给出导弹俯仰/偏航通道弹性振动模型

(7)

式(7)中,qzi(t)，qyi(t)分别表示俯仰和偏航通道第i阶振动的广义坐标,Qzi(t)，Qyi(t)，Mzi，Myi分别表示相应的广义力和广义质量,ωzi0，ωyi0，ξzi，ξyi表示对应的振动频率和阻尼比。

1.3 综合模型

由于弹性体导弹的弹性特征明显,在受到外界干扰时,容易发生弹性振动,从而改变弹体的姿态角并在一定程度上影响弹体的气动特性。把振动对气动特性的影响视为参数摄动,则结合式(1)和式(7)可以得到弹性体导弹俯仰/偏航通道综合模型为：

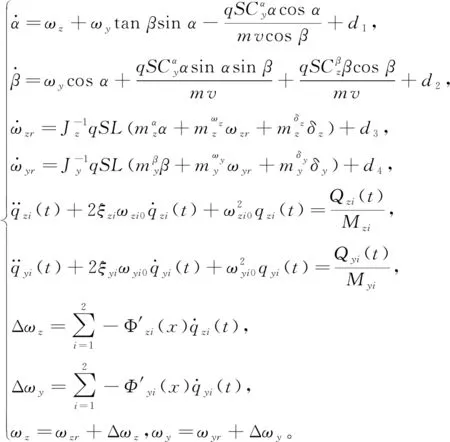
(8)

式(8)中,ωzr，ωyr分别为刚体俯仰和偏航角速度,为便于分析,把振动计入到干扰中,取系统状态为x1=[α,β]T,x2=[ωzr,ωyr]T,未知干扰和振动不确定性为D1、D2,控制量为u=[δz,δy]T,则弹性体导弹模型状态空间表达式形式为：

(9)

式(9)中，

假设1 干扰di及其一阶导数有界。

2 自适应减振控制算法

2.1 非线性干扰观测器

由于系统中包含干扰项,因此,需要设计干扰观测器对干扰值进行估计,考虑如下一阶不确定系统:

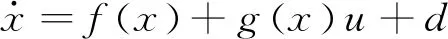
(10)

式(10)中,x∈R为系统状态变量,f(x)，g(x)为连续的函数,u∈R为控制输入,d∈R为未知干扰。针对上述不确定系统,干扰观测器设计为：

(11)

(12)

式(12)中,O(·)表示高阶无穷小,φ=(1-ϑ)/ϑ,ϑ∈(0,min(τ/(τ+n),1/2)),n≥2。

证明 :分两种情况证明。

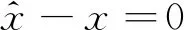
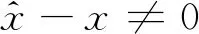
并且有:

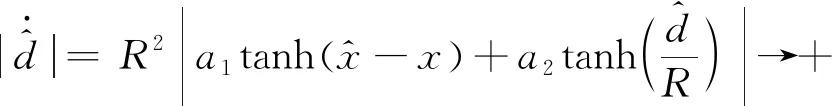
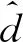
(9)

利用文献[15]设计的微分跟踪器,取n=2,则微分跟踪器的形式变为：

(13)

2.2 反演控制器设计

首先定义式(9)中每个子系统的跟踪误差

zi=xi-xid,i=1,2

(14)

式(14)中,xid为每个子系统的虚拟控制量。下面分两步进行控制器设计。

步骤1 对式(9)的第1个子系统跟踪误差进行求导,可得：

(15)

反演法控制需要对虚拟控制量进行求导。为避免求导所引起的复杂计算,采用式(13)所示微分跟踪器对x2c的一阶导数进行估计,得到可执行的指令x2d。

(16)

步骤2 对第2个子系统跟踪误差进行求导,可得:

(17)

假设2 干扰估计误差E1、E2以及虚拟控制指令x2c的导数估计误差E3均有界,即存在未知正数ηj满足‖E1‖≤η1，‖E2‖≤η2，‖E3‖≤η3,j=1,2,3。

下面对系统稳定性进行分析,选取Lyapunov函数

(18)

对式(18)进行求导可得：

因此,通过选取较大的hi,可保证系统状态跟踪误差收敛到一个足够小的邻域内。

2.3 自适应律设计

上面设计的控制器对刚体模型具有较好的跟踪控制效果,但是当系统出现弹性模态与刚体运动耦合时,并不能有效抑制弹体的振动。通常情况下,为了提高控制器的性能,控制器的增益应尽可能地高,但高的增益会激发弹体的弹性模态,减慢振动衰减的速度,甚至引起振动发散。因此,下面通过设计自适应律实时地调整控制器的增益,在刚体运动与弹性振动出现耦合时减小弹性模态对舵机的影响,以实现姿态跟踪与振动抑制的目的。

自适应控制律的输出是自适应参数ki,利用实际弹体与参考模型的相关状态信息,根据系统状态的变化,动态调整控制器的增益,降低弹性模态对刚体运动的耦合影响,提高系统的控制系能和鲁棒性。自适应律包含状态误差信号滤波项和一阶溢出项,自适应律的表达式如下：

(20)

式(20)中,bi为误差信号滤波项的增益,ci为溢出项增益,且bi、ci都大于零,-biyi为状态误差信号滤波项,-ci(ki-1)为溢出项。误差信号滤波项的输出信号yi是对实际弹体与理想参考模型的状态误差信号进行整流滤波得到的,参考模型选取为无不确定性和干扰的弹体刚体模型。yi的表达式如下：

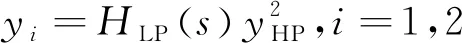
(21)

式(21)中,HHP(s)=s/(s+300)为线性高通滤波器,HLP(s)=3/(s+3)为线性低通滤波器,eir=‖xi-xir‖为实际弹体与理想参考模型之间的状态误差信号,xir为参考模型的状态。由式(21)可以看出,由于振动信号相比于刚体运动属于高频信号,经过式(21)的处理得到的yi的值反映了振动的强度,整流过程中存在信号平方项。因此,yi的值总是大于零的,而yi在自适应律中前面为负号,所以误差信号滤波项对自适应参数ki的影响总是使ki减小。结合式(20)来看,当振动逐渐衰减时,yi的值将变为0,即式(20)右边第一项为0,如果没有干扰影响,自适应参数ki=1。为防止ki的值减小为负值导致系统不稳定,将自适应律修改为：

因此,控制律式(15)和式(17)可修改为：

将新的控制律代入式(19)得：

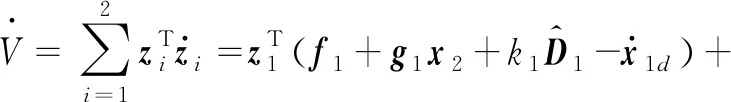
因为ki>0,Lyapunov函数的收敛性与上节相同,所以增加自适应律以后系统仍然是稳定的。

3 仿真分析

为了验证本文所提出算法的有效性,这里利用Matlab/Simulink环境进行仿真。设置仿真初始条件为:导弹初始姿态角[α,β]T=[0,0]Trad,初始姿态角速度[ωz,ωy]T=[0,0]Trad/s,参考指令和干扰设置为:

干扰观测器参数和自适应律参数如表1所示。振动阻尼比为0.02,振动频率为24 Hz,下面仿真时分两种情况进行。

表1 控制参数

情形一:振动广义坐标的初值为0,验证控制器在无振动情况下的控制性能。由于无振动情况下自适应参数k的值趋近于1,因此自适应律此时的作用很小,在受到干扰的情况下基于NDO的反演控制器应具有比较好的控制性能,保证导弹平稳飞行。施加正弦干扰得到的仿真结果如图1—图3所示。

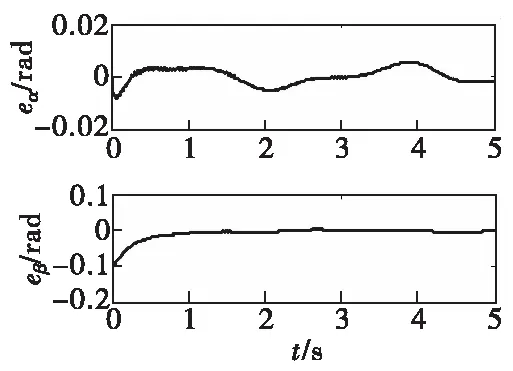
图1 攻角/侧滑角跟踪误差Fig.1 Angle of attack/sideslip angle tracking error

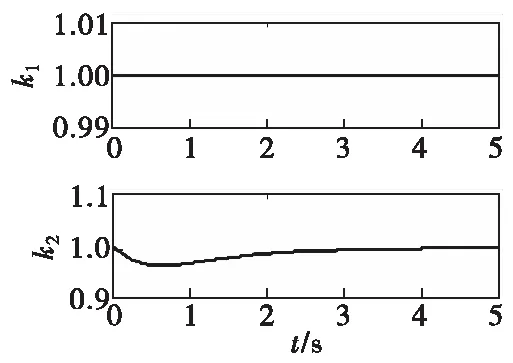
图2 自适应参数Fig.2 Adaptive parameters

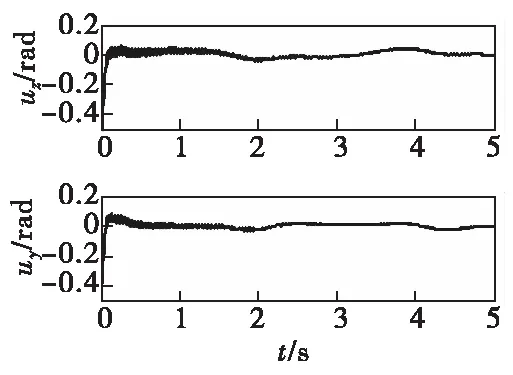
图3 俯仰/偏航舵偏角变化Fig.3 Deflection of pitching/yaw rudder angle

图1所示为攻角与侧滑角跟踪误差,其中攻角跟踪误差不超过0.006 rad,侧滑角跟踪误差不超过0.003 rad,稳定在一个很小的范围内,说明控制效果良好。图2所示为自适应参数k的变化。由于振动初始值设置为0,所以整个过程中振动非常弱,自适应参数近似等于1,自适应律对反演控制器的影响很小,可以忽略。由于侧滑角初始值和参考指令初值有较大的初始误差,导致舵偏角变化较大,激发了弹体的弹性模态,所以,图3中舵偏角存在持续的小幅振荡。

情形二:振动广义坐标的初值为0.01,验证控制器在振动情况下的控制性能。仿真结果如图4—图6所示。

图4和图5分别为俯仰/偏航通道的姿态角跟踪误差、一阶振动广义坐标和舵偏角指令,从图中可以看出,加入自适应律以后姿态角振动衰减速度明显加快,并且舵偏角指令和一阶振动广义坐标也明显减小,说明自适应律起到了很好的振动抑制作用。图6所示为自适应参数的变化,结合图4和图5可知,振动幅度比较大时,自适应参数减小以降低弹性模态与刚体运动的耦合影响,振动衰减到一定程度后自适应参数逐渐回归到1。另外,由于该方法是通过减小控制器增益来实现振动抑制的,因此,控制器的动态性能会受到影响,从图4(a)和图5(a)可以看出,尽管加入自适应律以后姿态角跟踪误差振动衰减更快,但刚体姿态角误差收敛变慢。

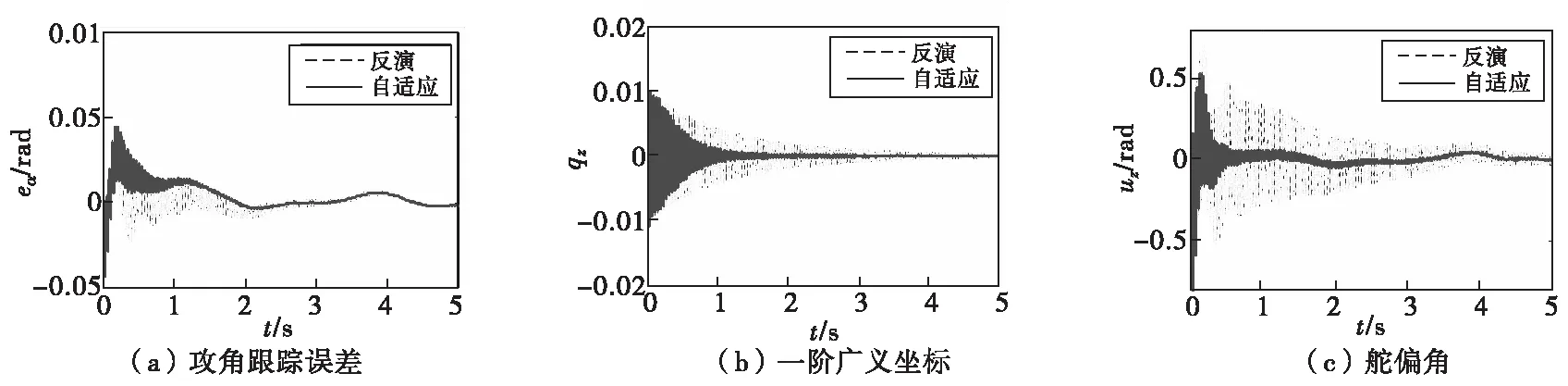
图4 俯仰通道Fig.4 Pitching channel

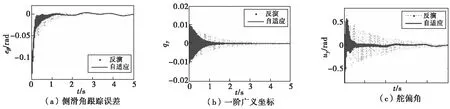
图5 偏航通道Fig.5 Yaw channel

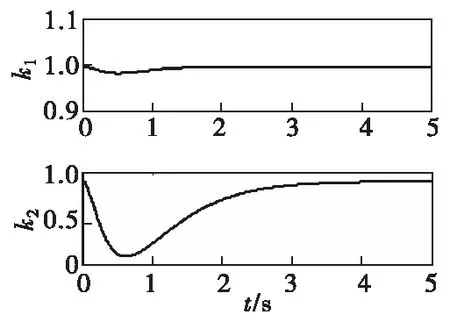
图6 自适应参数Fig.6 Adaptive parameters

4 结 论

本文针对带有非匹配不确定项的弹性体导弹姿态跟踪与振动抑制问题,提出了一种基于非线性干扰观测器的自适应反演控制算法,利用干扰观测器估计出干扰与不确定性,并通过自适应律动态调整控制器增益,可以有效克服干扰与弹性振动对系统稳定性的影响。仿真结果表明，所提出的控制算法能够有效抑制弹性振动的耦合影响,并实现导弹姿态的稳定跟踪。由于自适应律对控制算法增益的调节是与原控制算法增益直接相乘,因此,并未改变原有控制系统的设计原理,易于在工程中实现。