归纳与演绎，数学建模的“左膀右臂”

黄莲花

数学作为一门应用性很强的科学，在实际生活中的应用广泛，这种应用的广泛性靠的是数学模型。模型是把现实生活中的数量关系和图形关系抽象成概念和符号，它们作为数学研究的对象，推进了数学自身的发展。而数学自身的发展得益于归纳推理及演绎推理，依靠推理，数学才具有了严谨性。由此，小学数学建模应该重视归纳推理与演绎推理的教学，促进小学生建模意识的形成，最终提升其数学核心素养。

一、归纳推理——激发创新意识

小学数学建模教学，是从现实情境中抽象出数学问题，围绕着研究对象所呈现的数量关系、变化规律或空间形式，建立数学抽象层面的符号化结论。这个过程，归纳推理发挥着关键作用。所谓的归纳推理，就是从特殊到一般的推理方法，通过观察某类事物中部分对象以发现某些相同的性质，从而推导出该类事物具有这种性质。由此可以看出，模型建立的过程中，首先，寻找相关的特殊实例，使之成为教学研究的一类对象，这是归纳推理的重要内容;其次，引导学生发现这一类对象的共性之处，进而推理概括出符号化结论，即数学模型，这是归纳推理的重要结果。归纳推理的过程，猜测、验证、举例、观察、发现、归纳，学生在经历这个过程中，不仅由已知发现了未知，而且激发了学生主动思考、主动创新的意识。

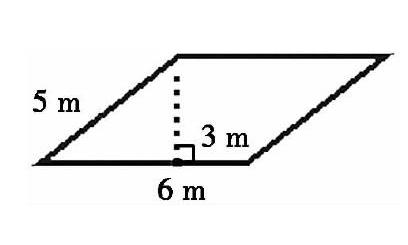
例如，教学人教版五上“平行四边形的面积”一课。学生从现实情境中抽象出数学问题“这个平行四边形的面积怎么求”之后，可进入如下几个环节的探究。

（1）验证本案例中的两种猜测“6×5”或“6×3”。引导学生先数方格，用剪拼法进行验证后，再借助填写表格和观察数据，不但发现“6×3”是正确答案，而且发现这个平行四边形的面积正好是底乘高的积。

（2）猜测平行四边形的面积计算方法。此时，笔者追问：“看来这个平行四边形的面积与它的底乘高的积有关系。是不是所有的平行四边形的面积都可以用底乘高计算呢？你有什么好办法验证下？”

（3）多个案例验证平行四边形的面积计算方法。引导学生数一数另外3个平行四边形的面积，并填写表格。（笔者通过多媒体展示方格纸图，并在图上出示标有底和高的平行四边形3个，图略）

（4）概括得出平行四边形的面积计算公式。此时，学生通过观察表格中面积与底和高之间的关系，可以推导出平行四边形的面积等于底乘高。

上述四个环节的教学，学生经历了两次猜测，两次验证，借助数方格和观察数据，学生从所举出的案例中，发现了每一个平行四边形的面积与它的底和高之间存在着一定的关系，即“面积=底×高”。由此，完成了归纳推理的过程。这样的设计，学生是通过对一个个不同實例的思考、操作、观察、分析，发现实例间的共性，进而推理得出结论的，学生的主动性、思考性都得以彰显，创新性得到培养。

二、演绎推理——培育科学精神

演绎推理是从一般到特殊的推理方法，其一般模式包括：大前提——已知的一般原理，小前提——要研究的论断，结论——根据一般原理，对特殊情况作出的判断。演绎推理在于证明结论而不在于发现结论，引导学生经历演绎推理的过程，可以让学生感受到数学结论的严谨性，培育敬畏科学的精神。

例如，在通过归纳得出平行四边形的面积等于底乘高后，教学不应止步于此，还需要完成如下几个环节的论证过程。

（1）继续追问，引导质疑。问题：仅仅举几个例子，就能确定所有的平行四边形面积等于底乘高吗，还是要继续举例，越多越好？或是有更好的方法？

（2）运用转化的方法探究。这个过程要处理好几个问题：一是为什么要将平行四边形转化为长方形？二是如何转化？三是转化前后图形各部分之间什么变了，什么不变？

（3）推导出面积公式。学生反馈交流后，围绕着怎样得出平行四边形的面积计算公式这一主旨，就有了演绎推理三段论的过程：长方形的面积等于长乘宽（大前提），平行四边形的面积等于转化后的长方形的面积，平行四边形的底和高相当于长方形的长和宽（小前提），所以，平行四边形的面积等于底乘高（结论）。

归纳得出的概念可以真也可以假，如何让学生领悟和感受真假结论是教学中的重点。从上述片段教学中可以看出，引导质疑是一个好的方法，通过寻找一个更好的解决途径，借助已知与未知间的关联，推断出未知，确保结论的正确性。从中学生也能体会数学思维的逻辑条理，学习科学方法，培育科学精神。

三、两者并举——积累活动经验

小学数学建模教学旨在培养学生的建模意识，形成建模思想，积淀数学基本活动经验。积淀数学基本活动经验，需要亲身经历和感悟归纳推理和演绎推理的过程，从而形成一定的思维模式，建立一定的数学直观。归纳推理在于由已知发现未知，演绎推理在于验证结论。归纳推理，本质上是从经历过的东西推断没有经历过的东西。经验不是靠教出来的，而是亲身经历过程，自己感悟出来的。当然，亲身经历过程未必有感悟，必须是这个过程有发生“故事”或者“事故”，引发了学生的思考，吸取了教训，才成为了经验。因此，这里的“故事”或者“事故”就成为了教学的焦点。

例如，情境创设蕴含实例与非实例问题，即上述猜测的两种答案“6×3”（底×高）或“6×5”（邻边×邻边），可看成是学生经历归纳过程中的一个“故事”。因为这个“故事”，维系了学生已有的经验，依据“长方形的面积=长×宽，长与宽是相邻的边，同时又是互相垂直的两条边”这个经验，推断出上述的两种答案。通过验证，借助方格纸中的“剪切法”又是另一个“故事”，经历这个过程，学生获得了新的经验，一是感悟到了平行四边形的面积不是与相邻的边有关，而是与相互垂直的两条边有关;二是积累了“面积就是面积单位的累加”的这一内涵的直观感知;三是为后面的演绎推理蕴伏了方法经验。接下来的再猜测再验证更是一个“故事”，学生获得了归纳的经验，形成“从特例入手，尝试性归纳探索一般规律或结论”的思维方式。最后，借助演绎推理过程验证归纳得出的结论;进而再推广到另外一些特例中去，获得实践活动的经验。

归纳与演绎，两者同样重要。经历归纳与演绎的过程，就是自主体验、感悟和积累“创新”与“逻辑”经验的过程，长期积累形成经验后，就会成为自己独特的思维模式，最终演变为一定的数学直观，从而在遇到类似的问题或新的问题时能下意识地回忆或联想，能作出一定的直观判断。归纳与演绎恰似建模的“左膀右臂”，在建立数学模型的过程中起着举足轻重的作用。

（作者单位：福建省厦门市文安小学   责任编辑：王振辉）