汽车座椅骨架固有频率的不确定度研究

余慧杰，许 飞，张鑫侃

（上海理工大学 机械工程学院，上海 200093）

汽车在行驶过程中受到各式各样的路面激励，这些激励通过车身地板最终传递到座椅上，从而使座椅产生抖动和异响。因此，对汽车座椅骨架固有频率的研究是改善车辆驾驶舒适性的一个重要方面。从上个世纪以来，研究人员开始对结构固有频率的不确定度进行了大量的研究，并取得了丰富的成果。P.Langer等[1]提出了一种区间随机方法，证明了几何不确定性相比材料参数对固有频率的影响更大，但是作者忽略了结构大范围波动可能造成的影响。X.G.Hua等[2]提出一种改进的摄动方法，利用随机性测量的模态参数，对结构参数进行统计识别，但是这种方法计算出的结果准确度较差，缺乏实用价值。Gilles Tondreau等[3]将随机子空间识别法应用到固有频率的不确定性上，证明了在简单结构中几何参数不确定时，固有频率呈现非正态分布，但是作者研究对象的结构都是简单梁结构，没有对复杂系统进行分析。汽车座椅骨架作为一种结构复杂、易于测量的结构，其固有频率受到多种不确定因素的影响，在工程上对其研究较少。

基于上述问题，本文针对汽车座椅骨架提出了一种有效的固有频率的不确定度研究方法。文中先是确定对座椅骨架固有频率有重要影响的主要因素，然后基于响应面代理模型，对汽车座椅骨架前3阶固有频率的不确定度进行研究，最后，讨论设计变量不同种分布对固有频率的影响。文中形成比较完善的座椅骨架固有频率不确定度的分析流程与方法。

1 建立有限元模型

对座椅骨架固有频率进行不确定度分析，首先要建立整椅有限元模型。由于座椅所有结构都由具有一定厚度的板筋件组成（如图1（a）所示），所以采用抽取中层面的处理方法。在有限元软件中用壳单元对薄壁件进行数学离散，建立详细的有限元模型（如图1（b）所示）。

图1 座椅骨架模型

有限元模型建立后，通过对真实的座椅骨架进行模态实验，获取座椅的振型和固有频率，修正和完善有限元模型。

2 不确定度模型

研究汽车座椅骨架的固有频率的不确定度，需要进行多次实验，假设对座椅骨架进行n次模态实验，得到这n次测量数据的平均值，标准不确定度为平均值的标准差。通过贝叶斯理论进行数学建模，见式（1）

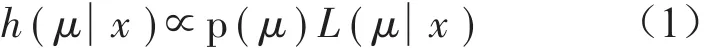
在工程中，常常用测量均值μ的后验密度函数h(μ|x)的期望E[h(μ|x)] 来表示被测量真值的估计值，用标准差来表示标准不确定度。通过对座椅骨架进行多次试验，经过数据处理得出先验均值μ0和均值的先验标准差τ，并设测量数据服从正态分布，得出

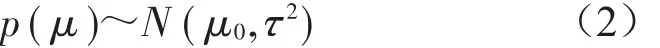
所以均值μ的先验密度函数为

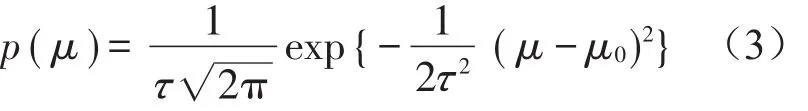
假设当前测量样本为X=（x1,x2…,xn）T，则样本的均值为

样本的标准差估计值为

则当前样本的联合密度函数为

将式（3）和式（5）代入式（1）中得出后验分布为

式中：

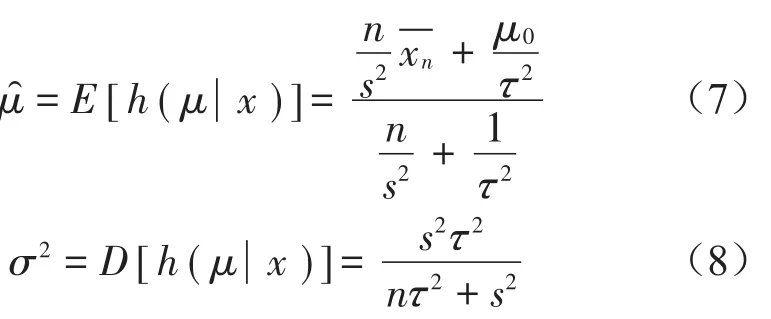
μ^为被测量值的估计；σ为标准不确定度。

3 座椅频率的不确定度研究方法

3.1 技术路线

为了对汽车座椅骨架固有频率的不确定度进行研究，需要进行试验设计，利用试验设计对影响汽车座椅骨架固有频率的所有因素进行筛选，之后利用筛选出来的设计变量构建响应面代理模型，最后，基于验证后的响应面代理模型对汽车座椅骨架固有频率的不确定度进行研究，并输出不确定度值。具体技术路线如图2所示。

3.2 模态影响因子筛选

由于影响座椅骨架固有频率的因素较多，为了能够将汽车座椅骨架中所有影响因素加以考虑，需要进行试验设计，从而筛选出有重要影响的因子重点考察。将座椅模型中的所有参数，包括各部件的厚度、材料弹性模量、泊松比、密度、弹簧单元6个方向刚度等作为输入设计变量，使用哈莫斯利设计方法进行首轮筛选[4]，获得前3阶固有频率的灵敏度分析图。图3给出各参数对座椅第1阶固有频率的灵敏度图，各参数的斜率越大表示对固有频率的影响越大。

通过筛选，选择座椅骨架的弹性模量、坐盆左侧板骨架厚度、导轨滚珠Z向旋转刚度3个影响因子作为设计变量，之后进行响应面拟合。

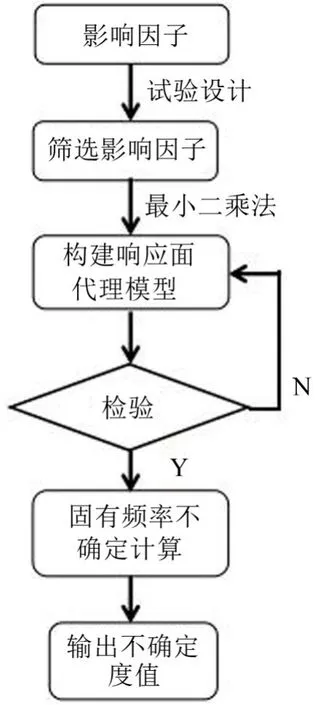
图2 不确定度分析流程图

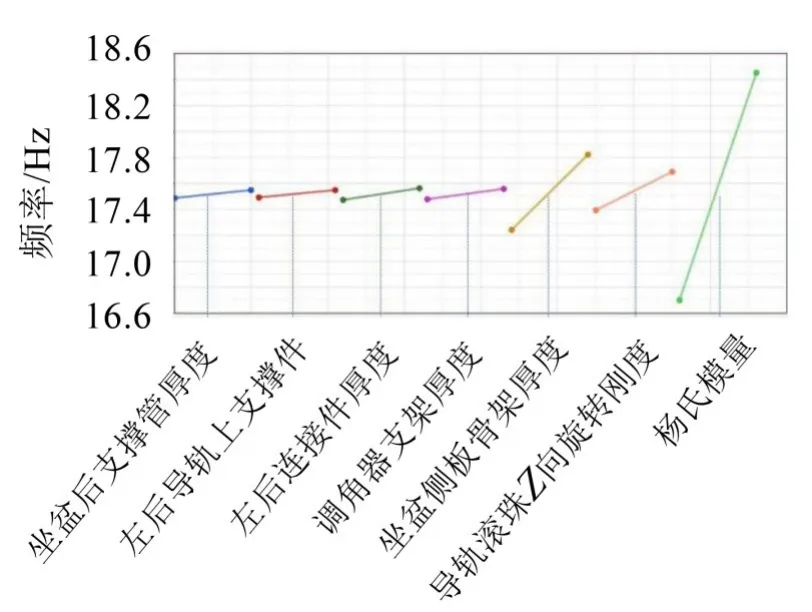
图3 第1阶固有频率灵敏度图

3.3 响应面拟合

建立响应面代理模型，就是在满足一定精度条件下，求解可以替代真实模型的响应函数，进而为快速研究不确定性、敏感性及方案优化服务。响应面代理模型是基于响应值与训练样本之间的最小二乘法拟合结果[5]。这个代理模型适用于表征真实模型的全局趋势，从而忽略局部震荡误差。常用的代理模型建模方法有多项式响应面法、Kriging法、径向基函数法等。在对汽车座椅进行不确定度研究时，考虑到拟合的精度和效率，采用二次多项式响应面模型，其数学表达式如下

公式中：f(x)为待求值；xi、xj为自变量；β0、βi、βij、βii是对应于各自变量的系数；ε是随机误差，即代理模型中的响应值与真实模型值之间的误差。根据训练样本进行建立代理模型时，基于最小二乘法可求得系数β，以满足代理模型与实际模型之间的响应偏差最小化。

在建立响应面代理模型时，采用1200组运用哈默斯利采样算法得到的样本组合，运用最小二乘法方法构建出高精度的响应面，最终得到3个设计变量与前3阶固有频率之间的响应面，之后对响应面进行拟合精度检验，将另一组样本点代入响应面并计算其误差，进而得到评价响应面精度的确定性系数为0.98242，均方根误差为0.06173。通过对比发现确定性系数大于0.92，均方根误差较小，从而证明响应面拟合效果较好。

3.4 基于响应面的固有频率不确定度研究

在响应面代理模型基础上，研究变量随机分布对前3阶固有频率的影响，最终完成对汽车座椅骨架固有频率的不确定度评价。假设设计变量满足正态分布，采用哈莫斯利法在响应面代理模型上进行模态提取计算，通过对设计变量进行104次设计组合，进而得到设计变量满足正态分布条件下，前3阶固有频率的估计值、不确定度值。为了检验前3阶固有频率估计值的正确性，通过模态实验获取座椅骨架实物模型的前3阶固有频率，通过对比研究结果，发现基于响应面代理模型计算出来的前3阶固有频率的估计值与试验值较为接近，最终确定研究的正确性。表1给出了前3阶固有频率的试验值、估计值和不确定度值。

表1 前3阶固有频率不确定度统计表/Hz

从结果中可以看出，固有频率的估计值与试验值十分相近，这说明响应面模型的精度满足要求。利用上面的这些参数，最终可以对前3阶固有频率集中趋势和离散程度进行评测。

4 设计变量满足不同分布讨论

由于工程实际中设计变量的分布除正态分布之外，也有可能存在均匀分布或三角形分布，为使不确定模型更具一般性，有必要讨论设计变量满足这2类分布的情况。通过将设计变量依次设为均匀分布和三角形分布，在响应面代理模型上进行104模态提取计算，进而计算前3阶固有频率的估计值、不确定度值。之后对设计变量为2种分布状态下的前3阶固有频率样本分布进行正态性检验，采用单样本Kolmogorov-Smirnov检验法，计算出相应的渐近显著性值。通过对比统计，最终完成不确定度评估。

表2为设计变量满足均匀分布和三角形分布状态下，前3阶固有频率的估计值、不确定度值和渐近显著性值。通过与表1进行对比研究，发现设计变量为上述3种分布状态下的前3阶固有频率的估计值和不确定度值相差较小,渐近显著性值均大于0.05，前3阶固有频率的样本分布总体符合正态分布。研究最终证明，设计变量分布不同对前3阶固有频率的估计值和不确定度值影响较小，前3阶固有频率的样本分布始终为正态分布。

表2 前3阶固有频率不确定度值和正态性检验表

5 不确定度结果验证

为了对研究结果进行验证，进一步提高研究的可信度，采用一种基于DOE和蒙特卡洛法的不确定度研究方法来验证。首先对汽车座椅骨架进行106次试验设计，得到106组样本数据，之后利用蒙特卡洛法对这106组样本数据进行不确定度分析，最终得到座椅骨架前3阶频率的估计值和不确定度值。

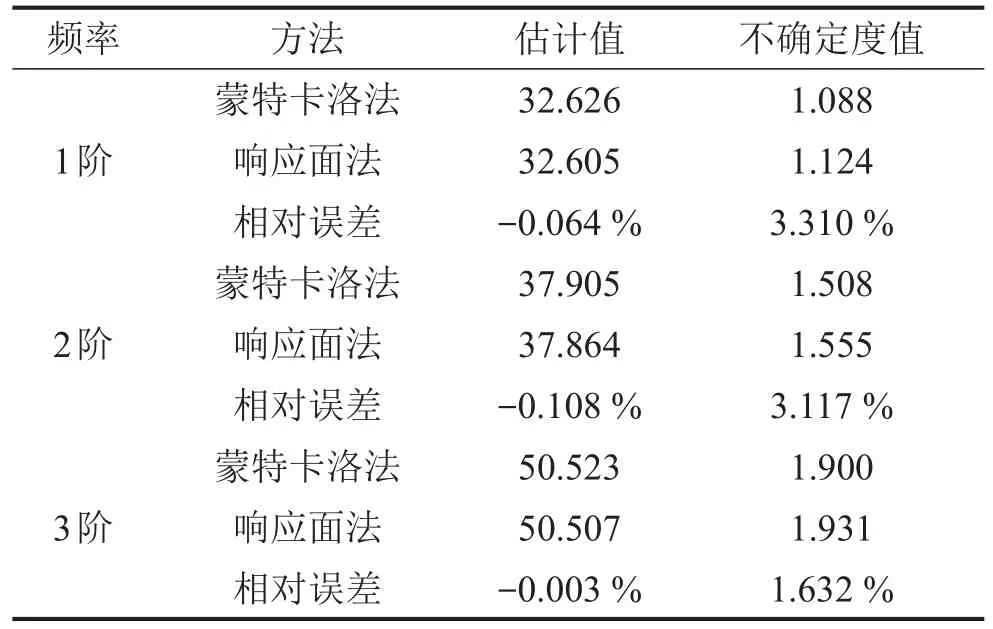
表3 前3阶固有频率不确定度统计表/Hz

表3为设计变量满足正态分布条件下，基于响应面法和蒙特卡洛法得到的汽车座椅骨架前3阶固有频率的估计值和不确定度值。通过对比2种方法的计算结果，发现基于蒙特卡洛法获得的前3阶固有频率的估计值、不确定度与基于响应面法计算出来的结果相差较小。因此可认为得到的结果可靠度较高，分析模型合理，最终分析结果可信。

6 结语

本文提出了一种基于响应面的模态不确定评价方法，首先建立汽车座椅骨架有限元模型，通过试验设计筛选出对前3阶固有频率影响较大的设计变量，构建响应面代理模型，之后基于响应面代理模型计算出前3阶固有频率的估计值和不确定度值。最后，为了对研究结果进行验证，采用一种基于试验设计和蒙特卡洛法的不确定度研究方法，最终完成对汽车座椅骨架固有频率的不确定度研究。

研究发现，设计变量的分布不同对前3阶固有频率的影响较小，设计变量不同分布时每1阶固有频率估计值和不确定度值差距较小，对响应的结果影响有限，固有频率的分布始终为正态分布。所以，设计变量的分布不同对于固有频率的最终分布影响效果不显著。研究结果为确定样本不同分布对固有频率的影响提供了理论指导。