无限大单板和空腔双板隔声量研究

黄梦情，陈美霞

（华中科技大学 船舶与海洋工程学院，武汉 430074）

无限大以及有限大单板和空腔双板结构[1-2]是隔声领域中常用的研究对象，比较有代表性的是单双层墙的隔声性能和质量定律[3-4]。

波传递法是一种非常经典的计算无限大板隔声量的方法[3]。它可以计算单层板、双层板甚至是多层板的隔声量[5-6]，但该方法也有自身的局限性[4]。当中间固体层比较薄时，可认为中间层中只有纵波传递，此时波传递法才能适用于斜入射。

除波传递法外，还将介绍另一种方法，这里将它称为“结构弯曲波法”。结构弯曲波法是将板的横向位移采用无限大板的形式[7]表示，再结合相应的法向速度连续性条件，代入板的振动控制方程，最后求解得到板结构的隔声量。

本文将采用波传递法和结构弯曲波法对无限大单板和双板的隔声量进行研究，得出2种方法的等效条件并对隔声量曲线的谷值点进行分析。

1 波传递法理论推导

1.1 无限大单板隔声的波传递法理论推导

在图1中，d表示媒质层Ⅱ的厚度。

沿空间任意方向行进的平面波表达式为

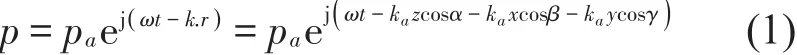
因此媒质Ⅰ、Ⅱ和Ⅲ中的声场可表示为：

媒质Ⅰ：入射波α=θi，β=90°-θi，γ=90°

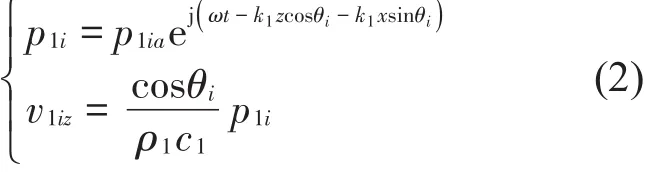
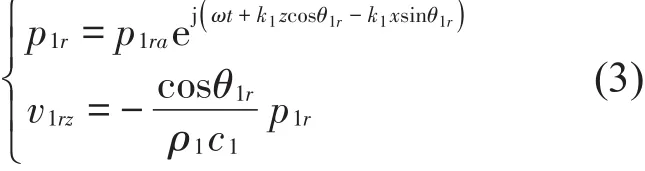
媒质Ⅱ：折射波α=θ2t，β=90°-θ2t，γ=90°

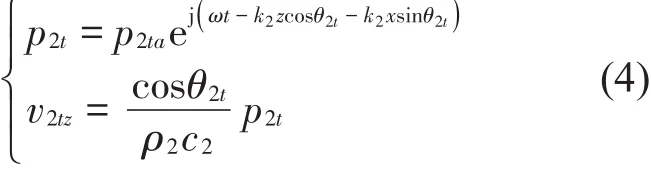
反射波：α=π-θ2r，β=90°-θ2r，γ=90°

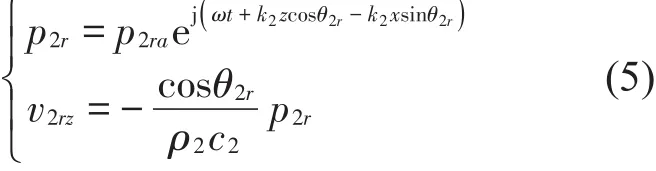
媒质Ⅲ：折射波α=θ3t，β=90°-θ3t，γ=90°

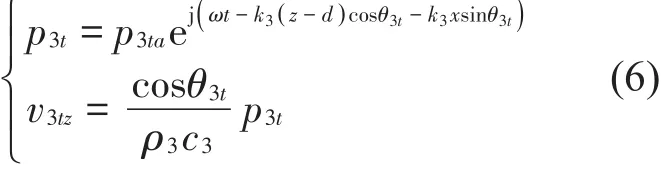
结合z=0和z=d处的声压连续与法向质点速度连续条件以及声波反射和折射定律，可得声压透射系数

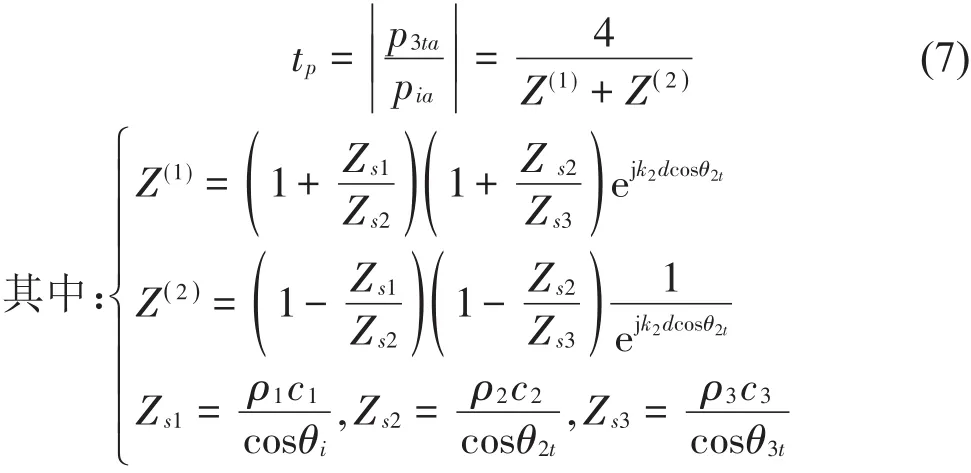
从而可得出声强透射系数tI

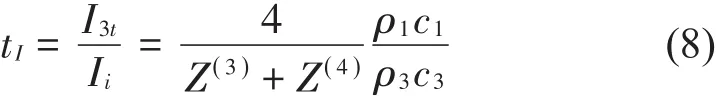
式中：

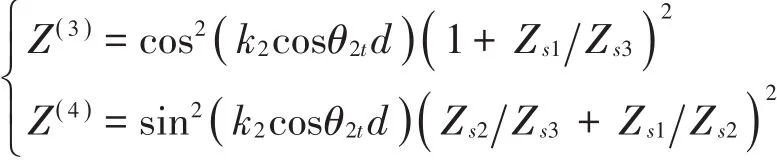
采用透射系数的倒数，并用分贝表示隔声量可得

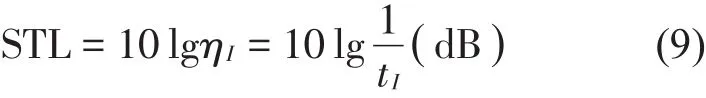
1.2 空腔双板隔声的波传递法理论推导

在图2中，d表示媒质层Ⅱ和Ⅲ的分界面，D表示媒质Ⅲ和Ⅳ的分界面。

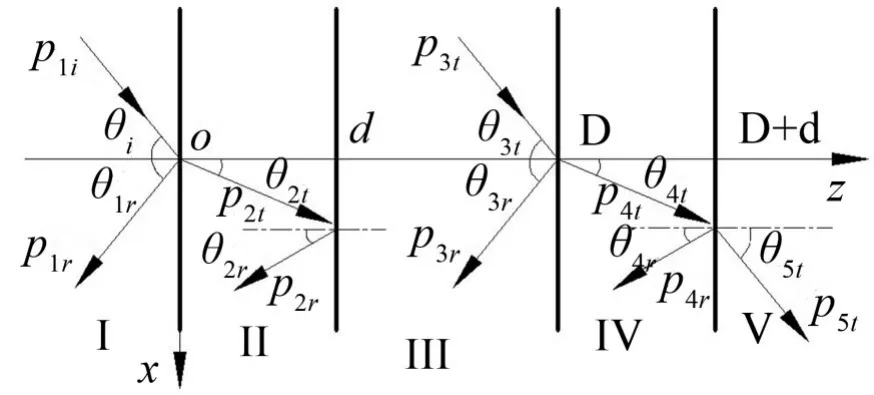
图2 空腔双板的波传递法示意图

针对图2所示的无限大空腔双板，波传递法的理论推导过程基本与1.1小节类似，因此对于声波透过空腔双板，计算得到的声强透射系数tI可表示为

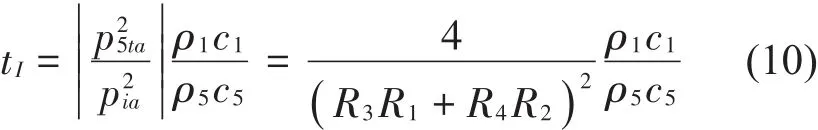
其中：R1、R2、R3和R4分别表示为

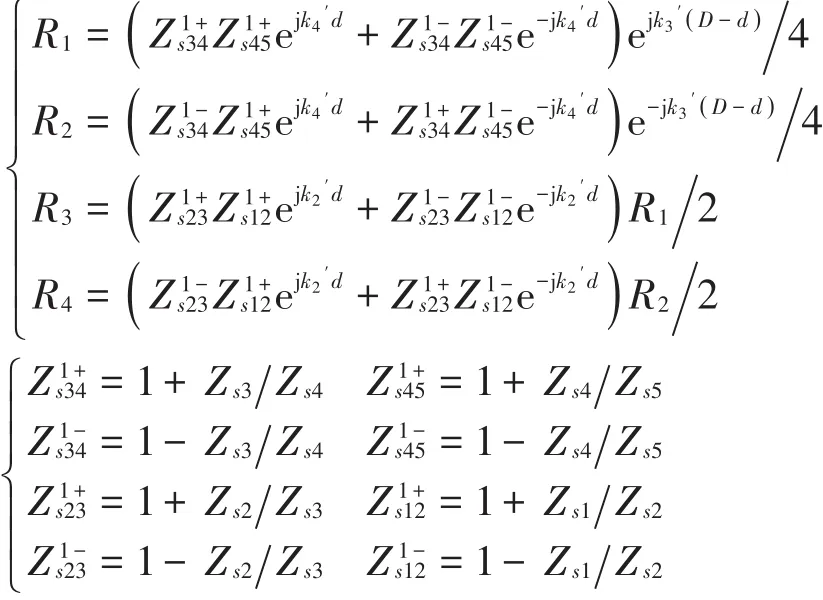
上式中的波矢分量k′和法向阻抗Zs的具体表达式为

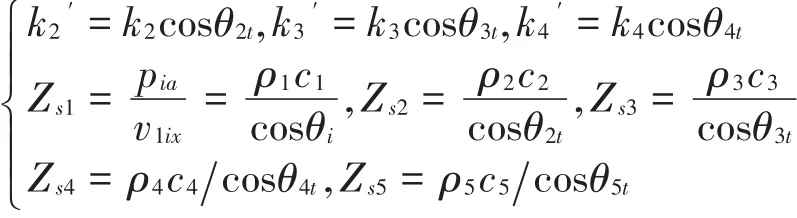
2 结构弯曲波法理论推导

2.1 无限大单板的结构弯曲波法理论推导

对于斜入射平面简谐声波，它的声压速度势函数可表示为

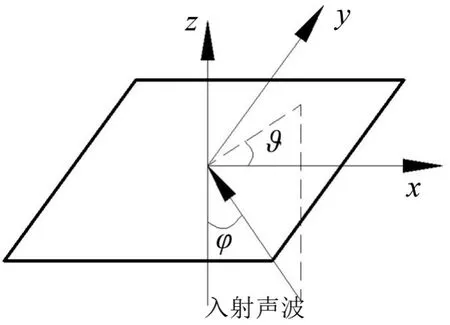
图3 无限大单板的结构弯曲波法隔声示意图（空间视图）

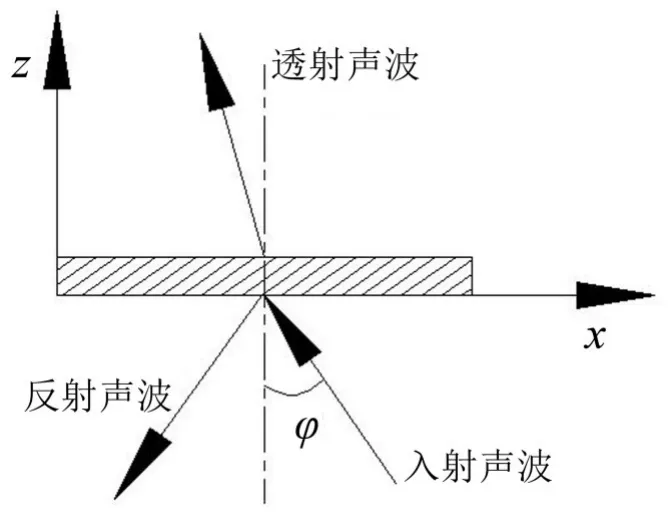
图4 无限大单板的结构弯曲波法隔声示意图（正视图）

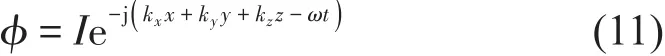
在式(11)中：I为幅值，ω为角频率，kx、ky和kz分别为入射声波在x、y和z方向上的波数分量：kx=k0sinφcosϑ，ky=k0sinφsinϑ，kz=k0cosφ。其中k0=，为入射域中声波的波数，c0为声波在入射域中的声速，φ和ϑ分别为俯仰角和方位角。

在入射声波的激励下，无限大薄板结构发生振动，向外辐射声波，其声振耦合振动控制方程为

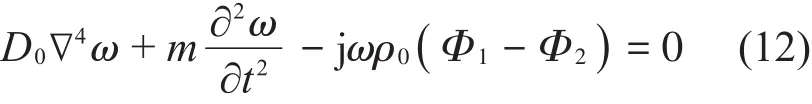
上式中ρ0为空气密度；ω、D0以及m分别为无限大板的横向振动位移、弯曲刚度和面密度。

入射声场和辐射声场的速度势函数可分别表示为

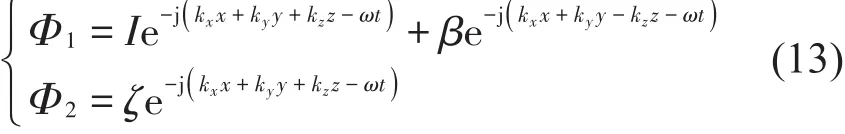
上式中入射声场中包含了入射声波和反射声波的速度势。

同时，将无限大薄板的横向位移表示为

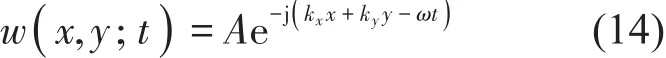
空气和薄板交界面处的边界条件为空气质点和板质点的法向速度相等，相应的连续条件为：在z=0处有

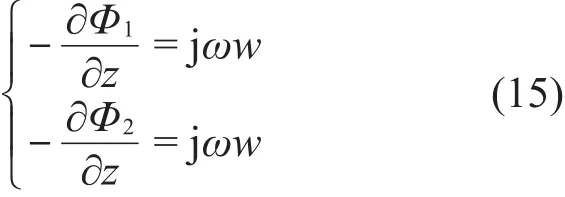
将式(13)代入式(15)中可得系数幅值关系式

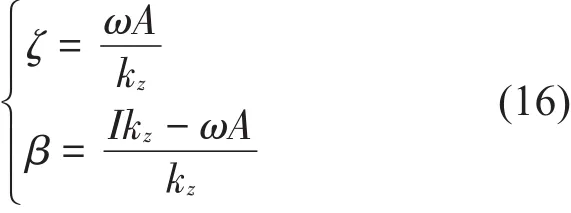
将式(13)和式(14)代入式(12)中，可得

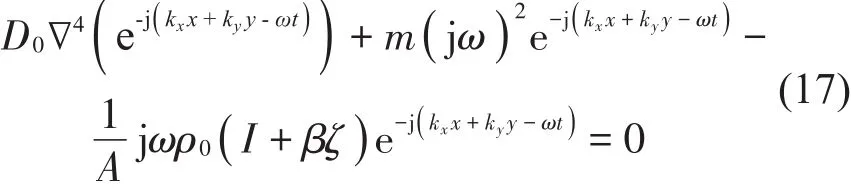
再将式(16)代入式(17)中，可进一步简化为

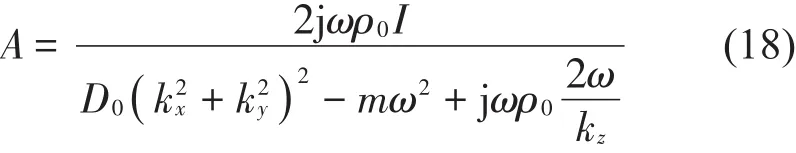
将式(18)代入式(13)，便可以得到入射声场和辐射声场的速度势。声压速度势和声压的关系为

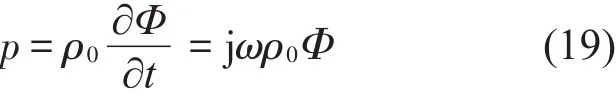
根据式(13)和式(19)，入射和辐射波的声压为

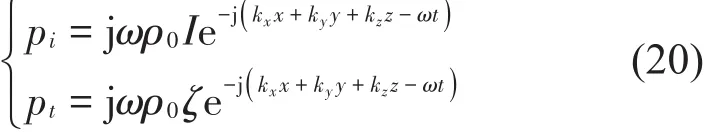
由于左右两侧均为空气，故声强透射系数tI可表示为

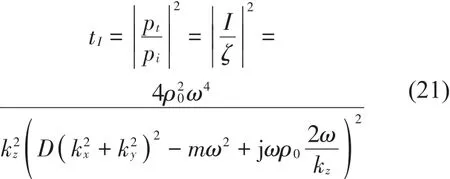
2.2 空腔双板隔声的结构弯曲波法理论推导

在入射声波的激励下，无限大空腔双板发生振动，并向外辐射声波，其声振耦合振动方程为

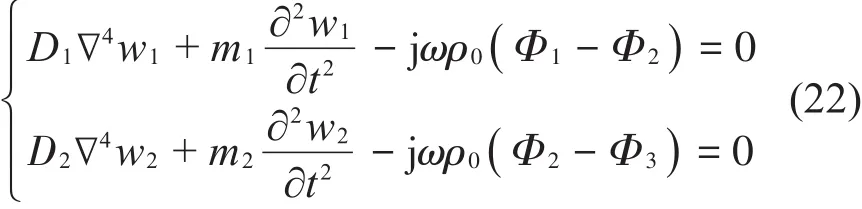
上式中：ρ0为空气密度以及分别为入射板和辐射板的横向振动位移、弯曲刚度和面密度。

入射声场、空腔声场和辐射声场的速度势函数可分别表示为

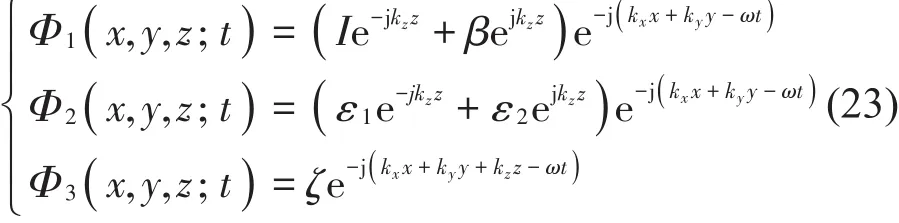
同时，无限大双板的横向位移可表示为

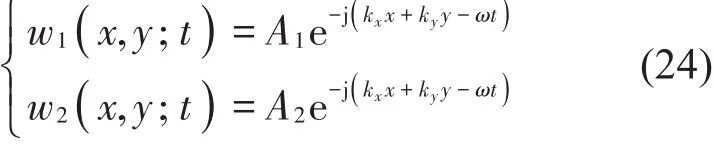
结合z=0和z=H处的连续性条件

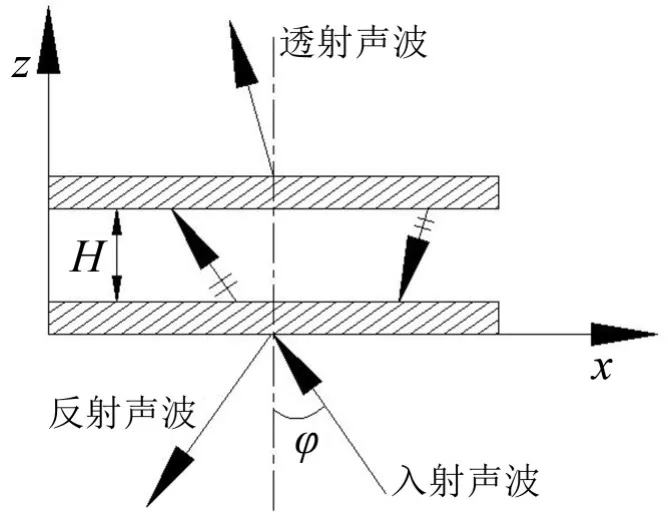
图5 结构弯曲波法的空腔双板隔声示意图

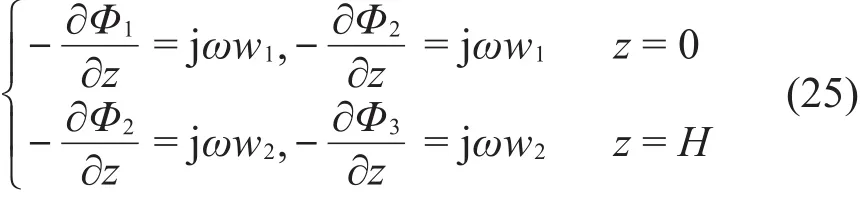
将式(23)代入式(25)中可得到如下的系数幅值关系式

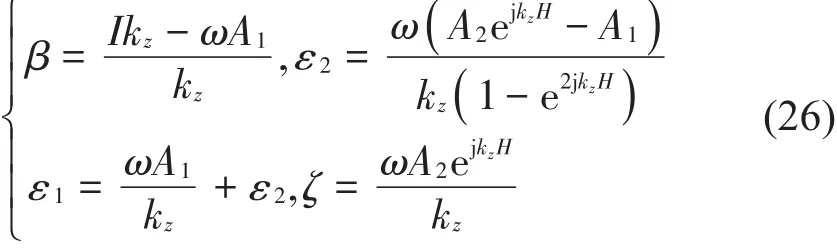
将式(23)和式(24)代入式(22)中，可简化振动控制方程

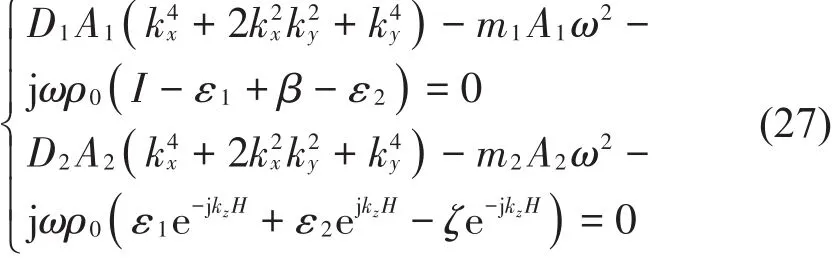
将式(26)代入式(27)，可将其进一步化简为

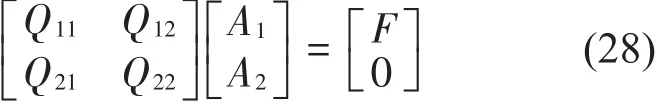
其中

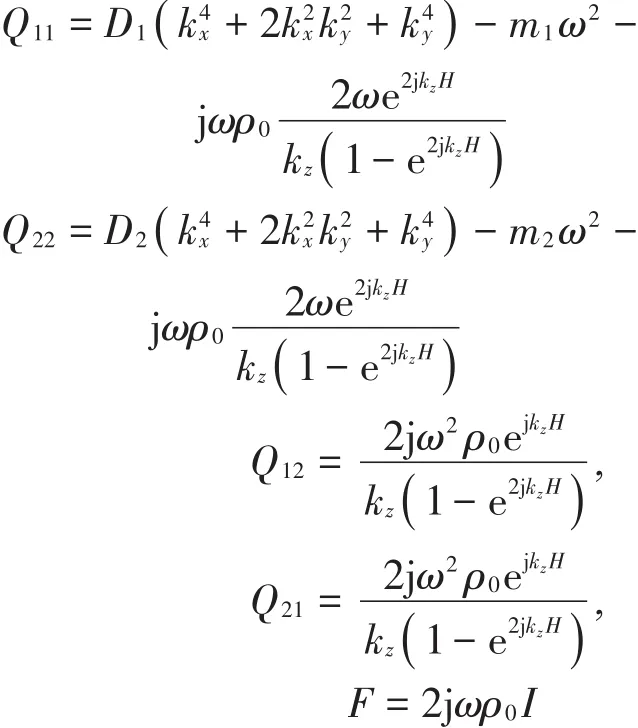
最后的声强透射系数为

3 无限大单层板隔声量对比分析

3.1 计算无限大单板隔声量的2种方法对比

单板采用铝材料，密度为2700 kg/m3，纵波声速为6260 m/s，泊松比为0.33，弹性模量为70×109N/m2，板厚取为0.01 m，两边介质都是空气，密度为1.21 kg/m3，声速为343 m/s，分别针对声波垂直入射以及30o和70o斜入射3种情况，得到对比结果如图6、图7和图8所示。

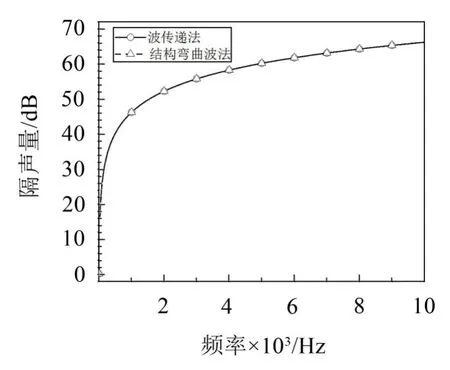
图6 基于波传递法和结构弯曲波法的单层板结果对比图（声波垂直入射，10000 Hz）

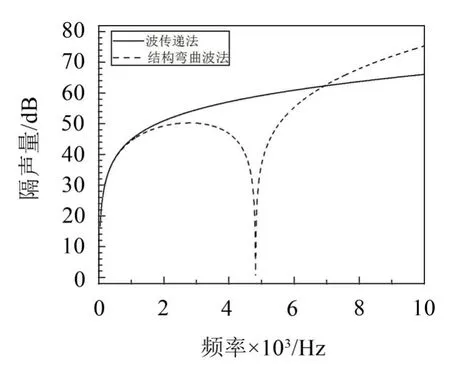
图7 基于波传递法和结构弯曲波法的单层板结果对比图（声波30o斜入射，10000 Hz）

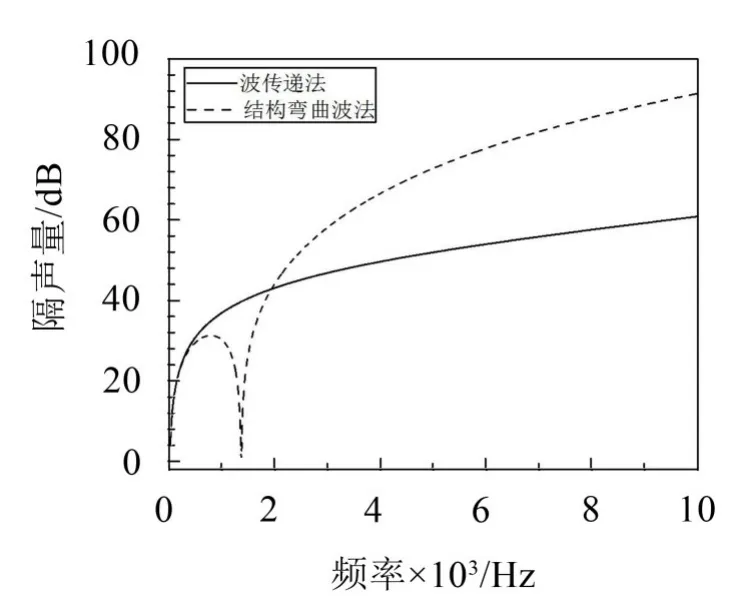
图8 基于波传递法和结构弯曲波法单层板结果对比图（声波70o斜入射，10000 Hz）

从图6、图7和图8中可以看出：当声波垂直入射时，基于波传递法和结构弯曲波法的计算结果在0～10000 Hz范围内，吻合得很好；当声波斜入射时，在低频范围内，两种方法吻合得比较好，但是进入中高频时，会出现板的吻合频率，2种方法计算的隔声量曲线吻合得很差。

同时，在声波斜入射的情况下，波传递法无法捕捉到板的吻合频率，而结构弯曲波法可以捕捉到板的吻合频率。这种情况下，基于结构弯曲波法的计算结果更准确一些。

3.2 声波垂直入射时2种方法的等效条件

声波垂直入射时，基于波传递法和结构弯曲波法计算出的隔声量曲线几乎重合，但是这2种方法的理论机理是不一致的，因此本小节将探讨2种方法的等效条件。

将2种方法的变量进行统一处理后，声强透射系数可分别表示为

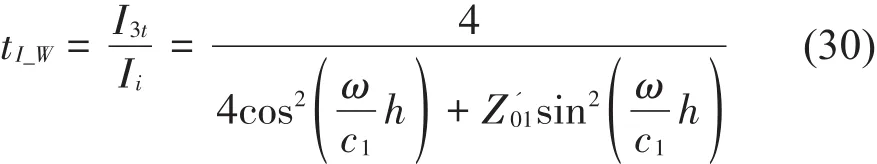
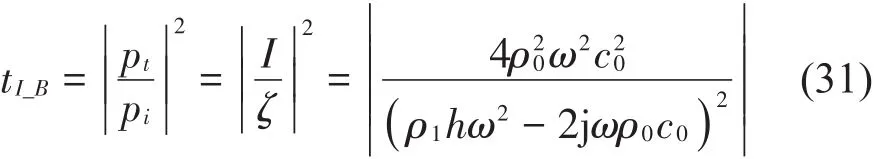
在式(30)和式(31)中，ρ0和c0为空气的密度和声速；ρ1和c1为板的密度和声速；h为板厚；ω为入射声波圆频率；tI_W和tI_B分别表示基于波传递法和结构弯曲波法的声强透射系数。

根据式(30)和式(31)，化简得

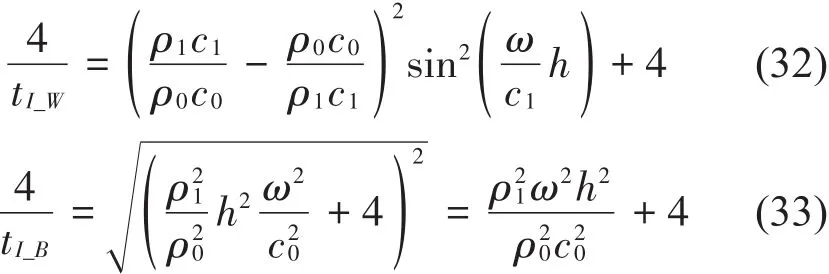
将式(32)和式(33)进一步化简，得出等效条件

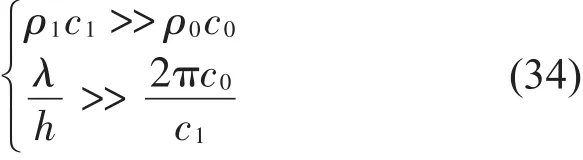
在式(34)中λ表示入射声波的波长。从式(34)中可以看出：当板的特性阻抗远大于空气的特性阻抗，同时入射波长与板厚的比值远大于空气声速与板中声速之比的2π倍时，波传递法和结构弯曲波法计算出的隔声量曲线基本是吻合的。此时，在声波垂直入射条件下，2种方法是等效的。

当入射声波频率非常高时，入射波长与板厚的比值变得很小，不再满足的条件时，这种情况相当于板厚变得很大，薄板条件不再满足，板厚对声波的传递影响很大，破坏了结构弯曲波法的成立条件。对于波传递法而言，声波的波长短一些，相当于介质层变厚，这依旧满足声波在介质交界面处和介质层中的传递条件，因此高频声波对波传递法的影响较小，它计算出的隔声量基本可靠。

当不满足ρ1c1＞＞ρ0c0条件时，也即周围流体对板的反作用变得很显著，这时不能忽略周围流体对板的影响，同时板自身也可能不再满足薄板条件。例如：较厚的复合材料板在空气中的隔声；有机玻璃板在水中的隔声；特性阻抗相差不大的各层板之间的隔声。在这种情况下，结构弯曲波法的计算结果存在不准确性，而波传递法依旧能适应这种变化。

3.3 无限大单板隔声量的谷值分析

当声波斜入射时，无限大单板的隔声谷值点对应的频率为板的吻合频率。薄板吻合频率[8]为

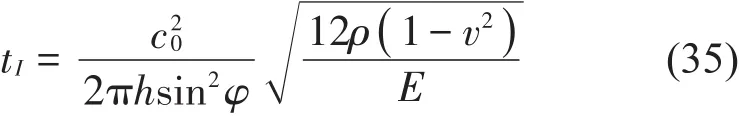
在式(35)中E和v为板的弹性模量和泊松比。

根据式(35)，计算出无限大单板的吻合频率为4810 Hz(30o)和1362 Hz(70o)，与图7和图8中的隔声谷值对应的频率4810 Hz(30o)和1362 Hz(70o)完全一致。

上面的计算对比说明：在声波斜入射时，采用结构弯曲波法能够捕捉到薄板的吻合频率。

4 空腔双板隔声量对比分析

4.1 基于2种方法所得的空腔双板隔声量对比

双板均采用铝材，密度为2700 kg/m3，纵波声速为6260 m/s，泊松比为0.33，弹性模量为70×109N/m2，板厚为0.002 m，中间层厚度为0.0215 m，两边和中间为空气，密度为1.21 kg/m3，声速为343 m/s，分别针对声波垂直入射以及30o和70o斜入射3种情况，得到如下的对比结果：

在图9、图10和图11中，实心圆代表“板-空腔-板”的共振频率；实心矩形代表空腔的驻波共振频率；实心三角形代表板的吻合频率。

从图9中可看出：当声波垂直入射时，波传递法和结构弯曲波法得出的隔声量曲线基本吻合。

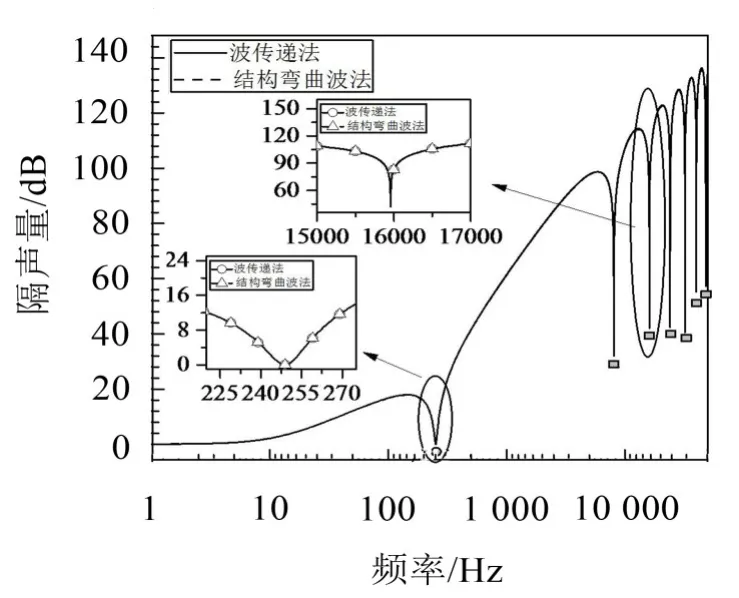
图9 基于波传递法和结构弯曲波法的双层板结果对比图（声波垂直入射，50000 Hz）

当声波斜入射时，在低频范围内，波传递法和结构弯曲波法的计算结果吻合得比较好；当进入中高频范围内时，出现驻波谷值和板的吻合频率隔声低谷，2种方法计算出的隔声量曲线不再吻合。波传递法可以捕捉到“板-空气-板”共振频率和驻波频率，但是无法捕捉到板的吻合频率，而结构弯曲波法可以捕捉到以上3种隔声谷值的频率。

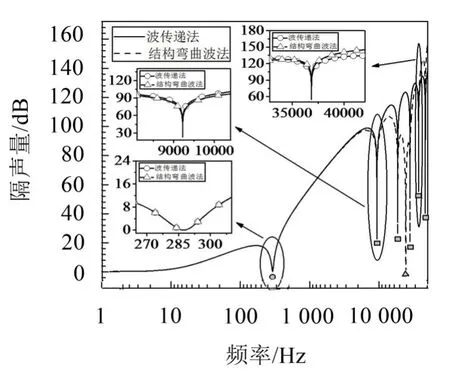
图10 基于波传递法和结构弯曲波法双层板结果对比图（声波30o斜入射，50000 Hz）

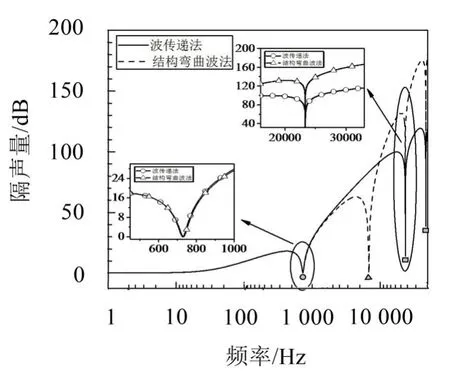
图11 基于波传递法和结构弯曲波法的双层板结果对比图（声波70o斜入射50000 Hz）

4.2 声波垂直入射时2种方法的等效条件

对于无限大空腔双板结构，声波垂直入射时的等效条件和无限大单板的等效条件一样，如式(34)所示。当不满足垂直入射的等效条件时，分别采用波传递法和结构弯曲波法计算空腔双板结构的隔声量，2种方法得出的隔声量曲线不能完全吻合。

4.3 空腔双板隔声量的谷值分析

首先，分析“板-空腔-板”共振频率，即实心圆标记出的谷值频率。当声波穿透没有任何连接结构的无限大空腔双板结构时，中间密封的空气腔对声传播起了重要的作用。此时，可将中间密封的空气层近似视为一个弹簧，它能够将入射板的振动传递到辐射板。中间空气层的等效刚度[3,9]为

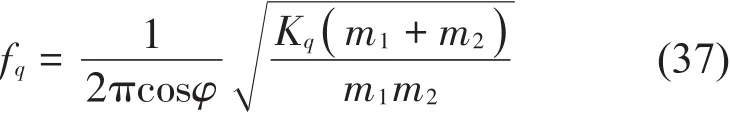
根据式(37)，计算出“板-空腔-板”的共振频率：249 Hz(0o)、287 Hz(30o)和728 Hz(70o)；采用本文2种方法计算的值为249 Hz(0o)、287 Hz(30o)和728 Hz(70o)；两者的结果完全吻合。从前面的计算结果可看出：波传递法和结构弯曲波法均能准确地计算出“板-空腔-板”的共振频率。

接下来，分析空气腔的驻波频率，即实心矩形标记的谷值频率。空气腔中的驻波频率可以由驻波的发生条件求得

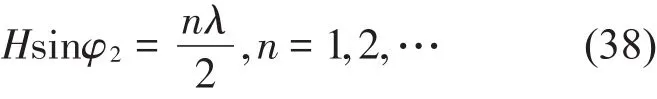
在不同入射俯仰角下，“板-空腔-板”的共振频率是不一样的，该共振频率的计算公式为[10]

其中：φ2为中间层的透射波与板面的夹角，这里用入射声波的入射角φ近似代替

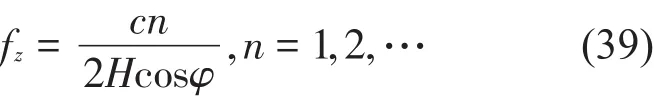
根据式(39)可计算声波入射角不同时的驻波共振频率。取2个共振谷值作对比，式(39)的理论计算值为 18421 Hz(30o，n=2)、23322 Hz(70o，n=1)；结构弯曲波法的计算结果为18432 Hz(30o，n=2)、23320 Hz（70o，n=1）；波传递法计算的结果为 18426 Hz(30o，n=2)、23350 Hz(70o，n=1)。从上面的对比结果可看出：波传递法和结构弯曲波法均能指示出空气腔的驻波共振频率。

最后讨论空腔双板模型中板的吻合频率，即实心三角形标记出的谷值频率。这里，同样根据无限大单板吻合频率的计算式(35)，可得到空腔双板的吻合频率为24051 Hz(30o)和6809 Hz(70o)，与图10和图11中的隔声谷值频率点24056 Hz(30o)和6809 Hz(70o)基本一致。

5 结语

对于无限大单板和空腔双板2种结构，当声波垂直入射时，基于波传递法和结构弯曲波法的隔声量计算结果几乎一致；当声波斜入射时，由于板弯曲波的影响不能忽略，因此基于结构弯曲波法计算出的隔声量更准确一些。波传递法和结构弯曲波法均能捕捉到“板-空腔-板”共振频率和驻波共振频率。同时，结构弯曲波法还能捕捉到板的吻合频率，而波传递法不能捕捉到该频率。

综上，针对薄板结构，当声波垂直入射且满足等效条件时，采用波传递法和结构弯曲波法计算得到的隔声量基本是一致的；当声波斜入射时，波传递法的计算结果在稍中高频范围内显得不可靠，主要是因为波传递法没有考虑板结构弯曲波的影响，所以结构弯曲波法的计算结果相对可靠一些。