立体几何中的角度会这样考查

陈国林 叶智群

(江西省南昌市东华理工大学理学院 330013)

纵观每年考题，关于立体几何中对于角度的考查是最为频繁，其实解决这一问题并不难，下面我们具体分析立体几何中各种角度之间的考查情况.

一、对空间中的两条直线间的夹角进行考查

(1)求三棱锥C-O1A1B1的体积；

(2)求异面直线B1C与AA1所成的角的大小.

解析(1)由题意可知，圆柱的高h=1，底面半径r=1．

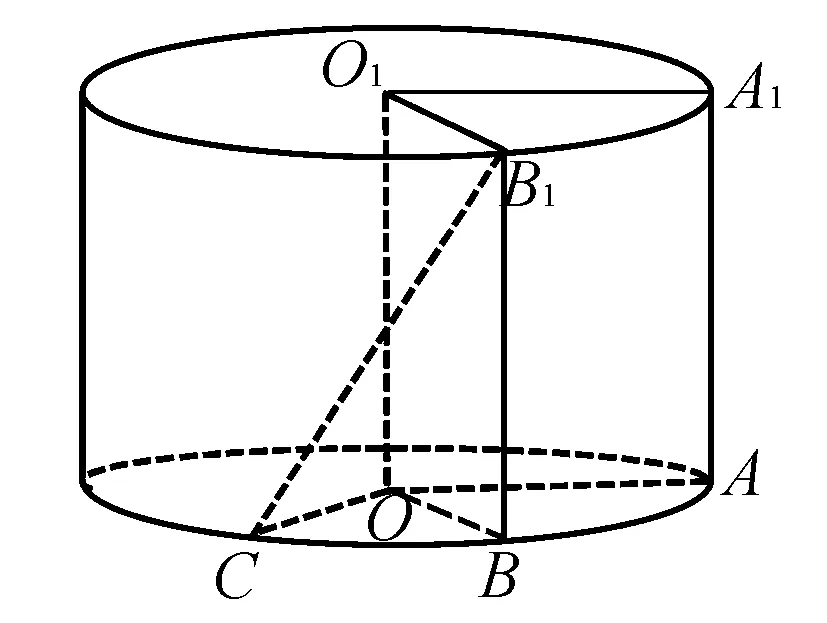
因为B1B⊥平面AOC，所以B1B⊥CB．

二、对空间中的线面角进行考查

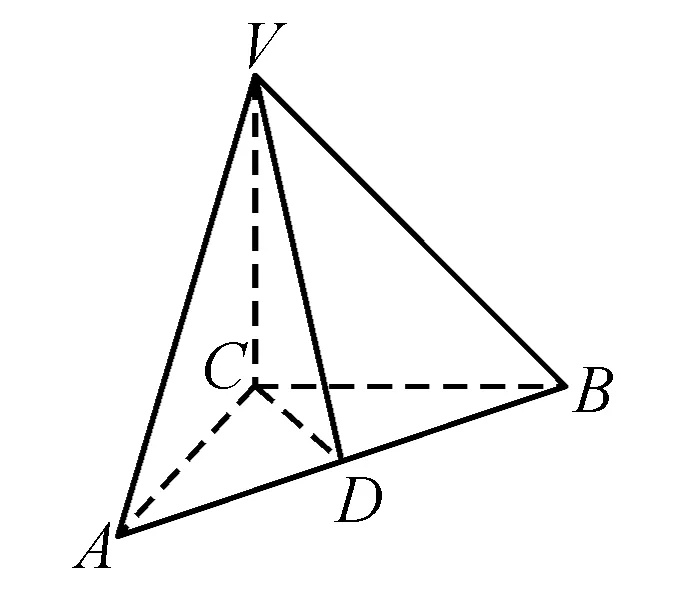
(1)求证：平面VAB⊥平面VCD；

解析(1)证明：∵AC=BC=a，∴△ACB是等腰直角三角形．又D是AB的中点，

∴CD⊥AB.又VC⊥底面ABC，∴VC⊥AB.

于是AB⊥平面VCD.又AB⊂平面VAB，

∴平面VAB⊥平面VCD.

(2)在平面VCD内过点C作CH⊥VD于H，则由(1)知CH⊥平面VAB.

设∠CBH=φ，在Rt△BHC中，CH=asinφ，

三、对空间中的面面角进行考查

(1)证明：MN∥平面PCD；

解法2：连接PM，因为AB=AC=1，点M分别为BC的中点，则AM⊥BC.

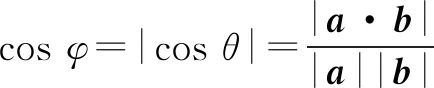
2)直线和平面所成角的求法

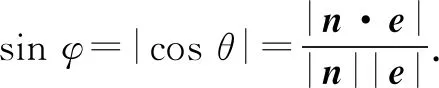
3)求二面角的大小

(2)如图②和图③，n1，n2分别是二面角α-l-β的两个半平面α，β的法向量，则二面角的大小θ=〈n1，n2〉或π-〈n1，n2〉.