评析 “气缸”知识点

商文洪

(江苏省苏州市吴江区汾湖高级中学 215211)

一、平衡问题

例1一圆形气缸，上盖一个重量不计的不漏气活塞.在活塞和缸底装有一根轻质弹簧，封闭着压强为p0的空气，(如图1所示)．气缸浮在水面时，以水面到活塞距离a，缸底到水面距离b，活塞面积S，弹簧倔强系数为k，水的密度为ρ.设将气缸缓慢地按入水中，当活塞距水面深度为多大时,气缸仍可能浮在水中．(气缸在浸入水的过程中温度不变,大气压强为p0)．

解当气缸浮在水面时，气体压强p1=p0.体积V=(a+b)S．且气缸的重量等于浮力，即Mg=ρgbs.设按入水中深度距水面为h时仍能浮在水中，此时气体体积V2=bS．由平衡条件得p0S+ρghS=p2S+ka,即p2=p0+ρgh-ka/s.根据玻马定律plVl=p2V2有p0(a+b)s=(p0+ρgh-ka/s)bS,解得h=(p0as+kab)/ρgbs.

点评从例题求解不难可以发现，解题的关键是对气缸进行正确的受力分析，通过平衡条件找出压强与其他物理量的关系，再用气态方程解得．

二、动力学问题

例2放在光滑地面上的气缸，缸体质量为2千克,活塞质量为1千克(如图2所示)．静止时活塞距缸底10cm，活塞面积为100cm2，外界大气压p0为1×105帕．现用水平推力F向左推活塞，活塞和气缸以共同的加速度向左加速运动，这时活塞和气缸底的距离变为8厘米，在不计活塞和气缸摩擦、不漏气及温度不变的条件下，求水平推力F.

例3如图3所示，气缸质量为8kg,活塞质量是2kg,活塞横截面积100cm2.当绳索松驰时，缸底空气柱长为0.5m，大气压强p0为1×105帕.活塞摩擦不计，g取10m/s2,现用160N的外力F通过滑轮拉气缸离地，求最后气缸内空气柱长度.

解当绳子松驰时，缸内气体压强p1=p0+mg/s体积V1=l1S.用力拉气缸使其离地时，由于F>(M+m)g故气缸整体向上加速，稳定后作向上的匀加速直线运动.对整体和活塞分别用牛顿第二定律得

F-(M+m)g=(M+m)a及F+p2S-p0S-mg=ma

解得p2=p0-[MF/(M+m)s]

根据玻马定律，p1V1=p2V2有(p0+mg/S)l1S=[p0-MF/(M+m)s]·l2S

解得L2=[(p0+mg/s)l1]/[p0-MF/(M+m)]

代入数据得l2=0.58m.

点评以上两例题可知此类气缸问题的解法是“整分结合”即先对气缸整体分析，后隔离活塞分析.利用牛顿第二定律分别列方程求解，得气体压强p与力之间的关系，这样问题就迎刃而解.

三、守恒问题

例4一水平放置在光滑面上的气缸，用活塞封有部分理想气体，气缸和活塞的质量都是m.如图4，现给活塞施一个向左冲量，大小为I使其向左运动，则在以后的运动中被封闭气体内能改变的最大值是多少.

解先根据动量定理，在给活塞冲量I，活塞产生的速度v=I/m,然后活塞向左运动，由于气体作用，活塞做减速运动，气缸作加速运动.当两者速度达到某一值时，气体压缩最大，内能改变也最大，活塞和气缸速度变化过程中，系统的动量和能量守恒.

把v=I/m代入解得ΔE=3I2/8m.

例5如图5所示，一封闭气缸上部为真空下部是一定质量的理想气体.中间活塞重为G，可在气缸内做无摩擦的滑动，距底高为h，气缸底部有一根电阻为R的电阻丝，现加上交流电u=Umsinωt,经时间t后活塞高度变为h′.试求：(1)气缸的内能改变多少？(2)气体的末温度T(设气体初温为T).

解(1)当电阻丝加热t秒放出的热量

又因为气缸上部为真空，所以F=G，故气体体积增大时是恒力做功，即W=Fs=G(h′-h).

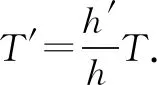
点评运用能量守恒的观点是解决热力学现象的基本方法之一.遇到上述气缸问题，需注意模型的识别，找出新旧模型之间的联系和本质区别，有些气缸问题表面看好象是气体性质问题，其实质应用能量守恒规律解决.

四、多缸问题

例6如图6所示，密封绝热容器中盛有27℃ 1个大气压的理想气体，现将容器中间用两个绝热而能自由滑动的活塞将容器分成A、B、C三个相等部分，每部分的体积均为V0．当A部分加热到227℃，B部分加热到327℃，C部分不变，则C部分体积是多少?

解加热重新平衡后，三部分压强仍然相等pA=pB=pC由理想气体状态方程可得

例7水平放置的固定气缸A、B内用活塞密封的空气压强都是p0，温度T0，体积分别为V1和V2.两个活塞的面积分别为S1和S2，用连杆连在一起，连杆所在空间真空.现将A筒空气加热到T1，B筒保持不变，求平衡时A筒内气压多大?

解对A容器，由理想气体状态方程得p0V1/T0=pAV1′/T1

对B容器，由玻-马定律得p0V2=pBV2′重新平衡后，对连杆和两活分析有

pAS1=pBS2

又变化前后气缸内气体的总体积不变，即V1+V2=V1′+V2′

多缸问题可以用“一分为二”、“合二为一”的方法去解.“一分为二”就是分别研究气缸内各部分气体状态参量的变化，找出它们各自遵守的规律；“合二为一”就是通过研究各部分气体间的关系，找出它们之间的物理和几何条件.如各部分压强相同，变化有前后总质量不变，容器总体积不变等等.最后联合求得.