生态城市发展质量评价方法研究

彭定洪,黄子航

(昆明理工大学质量发展研究院，云南 昆明 650093)

0 引言

自1971 年联合国教科文组织首次提出生态城市的概念以来，生态城市成为缓解全球生态危机的重要对策之一,受到相关政府部门与学术界的广泛关注。在对生态城市的研究中,对其发展质量进行评价是衡量城市规划、城市建设及管理成效的主要依据。鉴于指标体系的构筑和评价方法的选择是综合评价的两大核心，因此,结合生态城市建设的内涵和特点，对生态城市发展质量的评价指标和评价方法的探索成为国内外学者关注的焦点。柳映潇[1]利用物元可拓模型和ARIMA方法对贵阳市生态城市建设现状进行测度；翁翎燕[2]在全排列多边形图示法的基础之上对生态城市评价方法进行研究；Tang[3]从改进的TOPSIS方法、ESTI的层次动态模型和灰色关联度模型入手，进行了生态城市可持续发展的评价方法探索；Piwowarski[4]又根据VIKOR与TOPSIS的核心内涵，发展了欧洲城市可持续发展的评价方法。通过对以上研究成果的分析，在有关生态城市评价方法的研究中，以TOPSIS、ARIMA以及VIKOR等评价方法的应用尤为广泛，其主要原因是以距离测度为核心的评价方法，不仅可以考虑指标体系的结构以便于进行计算，而且可以根据距离差异体现出问题的不足之处。但经过其多年的发展，众多学者逐渐发现，此类方法极端参考解的选择，在应用中通常与实际情况并不相符。尤其在生态城市的评价中，其需要兼顾的经济发展与绿色环保本身就属于相互冲突的指标，极端的正负理想解就无法满足其参考解的选择。因此本研究提出了一种犹豫模糊EDAS评价方法，用以解决指标间相互冲突难以调和的问题。基于平均解的距离评价法由Ghorabaee[5]于2015年提出，该方法的优点在于将评价标准由极端的正负理想解更换为更具有实际意义的平均解，在参数难以调和的情况下，折中的平均思想显然更加符合实际利益。由于其显著的实用价值，该方法随即演变出了区间模糊EDAS[6]、2-type模糊EDAS[7]等拓展版本。但应用到生态城市的评价问题中时，以上的拓展版本还不足以应对在群体决策中难以达成专家共识这一缺憾，且在统计多年的发展数据时，经常会遇到数据缺失的问题。为了保证原始数据的真实性，本文选择可以将离散信息点作为计算元素的犹豫模糊集作为数据基础。并在此基础上将可以体现指标间相互联系的CRITIC客观权重确定法与其相拟合，提出了犹豫模糊EDAS-CRITIC法，作为生态城市发展评价的评价方法。

本文从生态城市建设中经济与环保相互冲突的特点入手，深入探讨问题产生的根本原因及指标体系内部相互制约的影响关系，综合考虑影响结果的根本因素，选择以人与自然协调性为出发点的DPSIR模型进行指标体系构建。发展了一种在考虑相关反馈特性的框架下，能够解决协调冲突指标的生态城市发展质量综合评价体系。

1 生态城市发展质量指标体系构建

1.1 DPSIR评估框架

DPSIR[8-10](驱动力—压力—状态—影响—响应)概念框架是由OECD和UNEP共同建立的一种对环境质量和生态系统进行评估的框架。该模型从系统的角度看待人和环境的反馈关系，将发展、人类健康、资源以及环境有机整合在一起，利用它们之间相互影响的关系引导其和谐共生。该模型还可以根据框架本身强烈的因果联系，清晰解释经济和环境之间的逻辑性，能够准确全面地对不同层面下各个指标间的反馈机制进行监测，以便能够解释经济与环境之间的内在逻辑关系，有利于从整体性角度反映城市生态发展质量。

在针对生态城市发展质量的评价问题中，本文所提出的DPSIR评价体系中，驱动力 (经济水平)是指引起资源与环境变化的内在原因，主要是社会经济活动中的内在动力与发展趋势；压力 (环境问题、社会问题)是指日常生活对周边资源和环境的影响，它是导致生态环境变化的直接原因；状态 (城市发展状态)是生态环境在驱动力和压力之下，整个社会、环境所呈现出的各种状况；影响 (城市发展评价指数)表示区域内各生态系统的各种状态对社会和环境的反馈结果与影响程度；响应 (政府政策)指为实现社会经济可持续发展而采取的积极有效的措施和对策。

1.2 构建生态城市发展质量评价指标体系

目前，我国对生态城市发展质量的相关研究已经引起了众多学者的重视，其中秦伟山[11]等基于制度等五个层面，构建了含有 35 项指标的评价体系对生态城市建设质量进行测度分析；罗辉[12]等通过发展水平指数模型、系统协调度指数模型和绩效模型，构建了生态文明建设评价指标对昆明生态文明建设进行评价；李从欣[13]从国土资源空间开发、资源节约利用、生态环境保护、生态协调和生态制度执行五个层面构建评价指标对省域生态文明建设进行综合评价；甘彩云[14]从 “五位一体”出发，归纳分析了厦门市生态文明建设状况，并据此提出了相应对策建议；David[15]又以P-S-R为框架，通过考虑指标间存在的相关性，进而构建了生态城市评价指标体系 (见表1)。为了反映我国生态城市建设质量，分析发展中的问题与障碍，并正确引导生态城市的规划与发展，本研究在分析众多研究成果的基础上，以DPSIR为评估框架建立生态城市发展质量评价体系，见图1。

表1 生态城市发展质量评价指标体系

资料来源：根据参考文献[11-15]整理。

图1 生态城市发展质量评价指标关系

2 研究方法

2.1 犹豫模糊EDAS评价模型

自模糊集[16]理论诞生至今，已被广泛应用到各类研究领域。随着社会的快速发展，客观事物的复杂性以及人们所掌握知识的局限性，致使学者们逐渐扩展了模糊集，出现了区间模糊集[17]、直觉模糊集[18]和区间直觉模糊集[19]等理论。但近年来，学者逐渐发现人们在进行决策时，经常会犹豫不决而且不能相互说服，致使决策难以达成一致。于是，Torra提出了一种模糊集拓展形式，即犹豫模糊集[20，21]。犹豫模糊集的隶属度并不是一个确定的值或服从某种分布，而是几个可能的隶属数值，这一特点显然更有利于解决数据不具有明显规律性的生态城市评价问题，且在处理评价过程中的群体信息时可有效避免因集结算子导致的信息丢失。

在以妥协思想为核心的多准则决策方法中，以TOPSIS[22]和VIKOR[23]的应用最为广泛，其核心都在于选择距离正理想解最近、负理想解最远的方案为最优选项。然而在实践中，我们总会遇到类似于生态城市评价问题中出现的评价指标相互冲突的问题，这就很难寻找到符合每一个指标的最优解，也就很难寻找到距离最为理想的备选方案。为了解决这一问题，本文根据犹豫模糊集EDAS方法，选择以平均解代替正负理想解，通过计算备选方案与平均解的正向距离和反向距离以表征各个备选方案之间的差距与优劣之处。选择正向距离值最大、负向距离值最小的方案，以此所得的最优选项不仅在效果上高于平均解，更可以避免因指标冲突而无法准确判断最优方案的问题。

2.2 犹豫模糊CRITIC客观权重确定法

除了指标具有冲突性这一问题外，DPSIR框架中指标间相互影响的因果关系也是评价生态城市问题的重点之一。目前在权重确定方法中应用较为广泛的专家评价法虽然都可以通过计算得出权重值，但只是给出了主观的指标权重，没能考虑到客观层面各个指标间的相互联系和相互影响，从而忽略了指标间本身存在的客观因素。而CRITIC[24]是一种通过计算指标绩效值与信息含量确定客观权重的计算方法，通过计算指标的变异大小和指标间的冲突性来综合确定指标的客观权重。因此，选择 CRITIC 法用以确定客观权重更加符合DPSIR框架中指标之间相互影响的特点。纵观多种研究成果，还没能提出一种犹豫模糊CRITIC法，本文将开展这项工作。

2.3 背景知识

定义1[22]令X为一给定的集合，M={u1,u2,…,un}为给定集合的N个隶属函数,则有关隶属函数的犹豫模糊集，即HM定义为:

HM={〈x,hM(x)〉|x∈X}

其中，hM(x)=∪u∈M{u(x)}是值域位于[0,1]上的一个集合,表示集合中X的元素x属于集合HM的若干种可能隶属度。为了表述方便,把有限论域X上的全体犹豫模糊集记为HFS(X),称hA(X)为A的犹豫模糊元,简写为hA。

定义2[22]对于任意两个犹豫模糊元h1、h2,它们的基本运算法则如下：

定义3 设ha、hb是任意两个犹豫模糊元，则犹豫模糊元ha、hb之间的距离公式为:

定义4[22]定义函数Θ:[0,1]N→[0,1],在参考集合X中犹豫模糊集X由N个犹豫模糊元组成 (H={h1,h2,…,hN}是在集合X上的一个犹豫模糊集)，在集合X中的一个扩展函数Θ在犹豫模糊集H中对每一个x都有：

ΘH(x)=∪γ∈{h1(x)x…xhN(x)}{Θ(γ)}

下面以一个简单的例子进行说明：

假设h1={0.5,0.6,0.7},h2=(0.5,0.6)，计算h1和h2的均值：

AMh1,h2=∪γ∈{h1×…xhN×}{AM(γ)}=

{AM(0.5,0.5)}∪{AM(0.5,0.6)}

∪{AM(0.6,0.5)}∪{AM(0.6,0.6)}

2.4 评价步骤

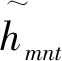
步骤二：确定二级指标权重。下面就EDAS方法中所需要确定的指标权重使用CRITIC法进行计算：

表2 决策矩阵示意

(1)对评价指标进行标准化处理。在评价体系中成本型指标和利润型指标具有不同的最优状态，为了能够准确地对评价对象进行评估，需要对指标进行标准化处理，以便进行统一计算。

对于效益指标，即指标值越大评价就越好的指标：

(1)

对于成本指标，即指标值越小评价就越好的指标：

(2)

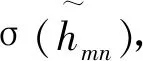
(3)构建相关系数矩阵。在本文所提出的CRITIC法中，主要运用相关系数刻画不同指标评价值之间的变化趋势。本文针对二级评价指标，构建线形相关系数矩阵R(见表3)。由于所给出的评价值为犹豫模糊数，传统的相关系数不能满足本文的需求，因此受Hausdorff距离测度思想启发，本文重新定义了一种犹豫模糊相关系数，该系数既可以避免主观增添HFE中元素，也不需要对HFE进行顺序排列。

定义5 设X为参考集，hA与hB为在集合X上两个给定的HFE，则犹豫模糊相关系数C(hA,hB)为：

其中，#hA为hA中元素的个数，#hB为hB中元素的个数。

表3 犹豫模糊相关系数矩阵

(4)计算信息量。即对二级指标cmn所包含的信息量Hmn进行计算：

(3)

(5)计算犹豫模糊权重。在这一步中，默认指标所含信息量的大小即为指标的犹豫模糊权重，其指标信息量的标准化将在后面的步骤中进行处理。当Hmn越大时表明指标cmn所含的信息较多，对应的权重就应该越高：

wmn=Hmn

(4)

式中，wmn表示二级指标cmn的权重，Hmn代表指标cmn所包含的信息量。

步骤三：通过计算评价指标的评价值，构建平均解矩阵AV：

AV=[AVn]1×n

(5)

其中：

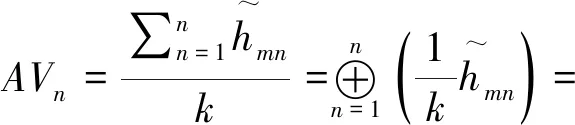
(6)

若cmn为利润型指标，则：

PDAmnk=

(7)

NDAmnk=

(8)

若cmn为成本型指标,则：

PDAmnk=

(9)

NDAmnk=

(10)

从客观评价值的角度来看，所构建的正向距离矩阵 (见表4)表示为在生态城市质量评价指标体系中，部分指标超出平均参考解的数值；负向距离矩阵 (见表5)表示为在生态城市质量评价指标体系中，部分指标低于平均参考解的数值。另一方面，从主观感性心理角度分析，也同样可以将其视为在对城市进行评价时，高出均解参考解看作收益，即为考虑了专家组对这一城市发展质量的满意程度；低于均解参考解看作损失，为专家组对其失望不满的程度。

步骤五：将步骤四中所得到的距离矩阵PDAmak和NDAmak中的距离分量进行求和计算得：

(11)

(12)

步骤六：计算所有备选方案的评估得分ASk。

(13)

(14)

(15)

在公式 (15)中，求得0≤ASk≤1。此处的平均思想也同样体现了在生态城市质量评价过程中，平衡冲突指标及折中满意与失望的思想。

步骤七：根据计算所得的评估得分ASk对备选方案进行排序。其中，得分最高的方案为最优选项，并且可以根据得分对备选方案划分等级，明确优劣。

在图2所给例子中共有4个备选方案和两个利润型指标，每个方法在不同指标下的PDA和NDA计算值都会显示在图中。如果一个方案的PDA>0，相应的NDA值=零。当NDA>0时，也有PDA = 0。可以看出在两个指标上都有PDA值的A3是最好的，而在这两个标准上有NDA值的A2是最差的选择。对于A1和A4的排名，我们还根据所提出的方法获得评估分数。

表4 正向距离矩阵

表5 负向距离矩阵

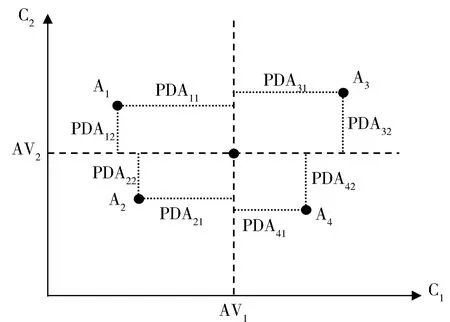
图2 犹豫模糊EDAS方法评价示意图

3 算例实证与对比分析

3.1 研究区域概况

云南省地处我国西南，是一个自然景观丰富，城市建设环保的省份。其经济发展的主要支柱就是以自然山水为主的旅游业，这就致使云南省的经济发展是可以和绿色环保相互协调、相互依存的。正是因为认识到了这一优势，云南省各市的发展也一直是以建设生态城市为目标。但在生态城市的建设过程中，云南各市始终都没能形成一个完备的建设评估体系，自然也就无法衡量其发展质量及找出发展短板。因而，本文选取云南省内建设较好的昭通、曲靖、昆明、玉溪四个城市为例，根据本文构建的综合评价体系，衡量其生态城市发展质量，并找到发展过程中的不足之处。

3.2 数据来源

在本研究中，根据所构建指标体系给出的评价指标，除了GDP增长率、人口密度及经济发展指数等客观数值由 《云南统计年鉴2010—2015》和 《中国统计年鉴2010—2015》给出外，余下数值均为主观评价值。为了保证主观评价值的客观性与真实性，本评价活动邀请来自环保厅和高校研究机构的五名资深专家组成评估组，为四个城市A1、A2、A3、A4进行打分。其中整体环境压力指数这一指标选择以5年的数据为基础，通过加权计算的方式得到具有代表性的数值。

3.3 评价步骤

得到标准化后的决策矩阵建立犹豫模糊决策矩阵D：

步骤二：运用犹豫模糊CRITIC法计算犹豫模糊指标权重。

得到一级指标和二级指标的犹豫模糊权重，将一级权重与二级权重相乘得到最终权重:

根据步骤三构造平均解矩阵AV:

AV[(0.34,0.37),(0.34,0.33,0.34),(0.72,0.73),(0.60,0.58),(0.43),(0.55),(0.44,0.47,0.46),(0.61),(0.48,0.52),(0.56),(0.35),(0.51,0.56),(0.52,0.34),(0.60),(0.73),(0.66,0.54),(0.54),(0.49,0.50,0.79)]

步骤四：利用公式 (6)～ (10)得出正向距离矩阵与负向距离矩阵:

通过计算得到的正向距离矩阵可以发现，昆明市的18个评价值中有5个与正向均解的距离均为最突出，玉溪市和曲靖市在经济衡量指标上与之存在部分差距，但在绿色衡量指标中玉溪市与昆明市之间并无明显差距。

最后通过公式 (11)～ (15)得出ASk并进行排序，经过计算得到:

AS1=0.5538,AS2=0.5688.AS3=0.6736,AS4=0.6715。因此，AS3>AS4>AS2>AS1证明，第三个城市是发展质量最好的生态城市。

通过对以上评价结果的分析可以得出：①通过计算过程与原始数据来看，昆明市的绿色、环保类指标得分值与玉溪市不相上下，与曲靖市与昭通市存在差距。之所以会在排名上出现差距，主要是玉溪市的经济发展相较于昆明市比较弱势，经济发展指数与政府治理指数也都偏低，综合之下昆明市的总体发展态势领先于其他三市。②从四个城市的排序及评估得分可知，昆明市与玉溪市同属于建设质量较好的生态城市，昭通市与曲靖市属于发展质量一般的第二梯队。主要原因均为经济发展的迟缓，绿水青山同为云南省各市的环保优势，但如何在不损坏的基础上使其成为经济成长的动力，正是昭通市与曲靖市的城市建设难点之一。③单一的旅游产业建设也同样是云南各市的经济发展指数普遍偏低的原因之一，应利用绿色资源，综合发展多结构、多框架的产业经济，也同样可以提高生态城市的发展质量。

3.4 对比分析

本文提出的犹豫模糊EDAS方法是在TOPSIS方法的基础上进一步体现妥协思想，使用平均解替代正负理想解作为评估标准，用以解决生态城市发展质量评价问题中出现的指标冲突问题。除此之外，本文还将该方法与妥协思想的另一代表方法VIKOR相对比，证明犹豫模糊EDAS方法在生态城市发展质量评价中的优越性。因篇幅限制仅给出犹豫模糊TOPSIS和犹豫模糊VIKOR方法的排序结果。

(1)Xu[25]等提出了一种在犹豫模糊环境下的TOPSIS方法，根据本文所给出的评价值利用该方法进行计算，得到这四个城市的贴近度以及排序结果：CC1=0.5027,CC2=0.4135,CC3=0.4022,CC4=0.5156，可得A4>A1>A2>A3。由此可以发现，在犹豫模糊TOPSIS方法计算下得出的最优城市为A4。通过对指标的分析可以发现，A3虽然在经济发展上逊于A4,但在绿色环保方面却在所有城市中是最为突出的。由此可知犹豫模糊TOPSIS方法在取理想解时采用了极端取法，导致在判断指标冲突性的问题时会出现极端的偏向一面的情况，无法给出兼顾多面的评价结果。且在Xu提出的方法中采用添加HFE和降序排列的方式进行处理，这也同样导致结果的偏差。

(2)Liao[26]等提出了一种适用于犹豫模糊集的VIKOR方法，该方法也是同样遵循妥协原则的多准则决策方法。针对本文所提出的评价问题应用该方法进行评价得出：CC1=0.3742,CC2=0.3213,CC3=0.4759,CC4=0.4033，排序结果为A3>A4>A1>A2。根据结果分析可得犹豫模糊VIKOR方法所得出的最优城市与次优城市都为A3与A4。从指标的评价值中也可以看出A3的经济发展水平排名靠前，环保指标也优于A2。从DPSIR兼顾性的角度综合分析，A3确为发展质量最高的生态城市，证明本研究所提出的方法具有一定的准确性。

4 结论

(1)通过对云南省生态城市发展数据的收集与分析，根据生态城市建设目标的要求，结合专家咨询与发展需要，建立了系统、科学的生态城市发展质量评价指标体系。并运用犹豫模糊CRITIC法确定指标权重，以犹豫模糊数为基础构建评价矩阵，形成了可以解决冲突指标问题的犹豫模糊EDAS-CRITIC综合评价模型。并进行对比分析，证明研究方法的准确性与合理性。

(2)以云南省为例，通过对四个城市的GDP增长率、经济发展指数以及建成区绿地覆盖率等指标进行调查、收集、研究分析该城市的文献资料，根据生态城市发展质量评价体系，应用EDAS-CRITIC评价模型进行评价，得出排序结果。说明云南省内生态城市建设质量最高的城市为昆明市，其次为玉溪市，与城市发展现状相符。验证了该评价理论的系统性、可行性与实用性，可为其他生态城市的规划建设提供评价依据。