一种带弹托的尾翼稳定装置的设计及动力学仿真分析*

刘瑞卿，杨 力，陈红星，赵雨馨，张培建，鱼 博

(西安现代控制技术研究所， 西安 710065)

0 引言

尾翼稳定装置是制导炮弹的重要组成部分。制导炮弹在炮膛内点火发射时，尾翼处于折叠状态并被约束；当炮弹出炮口之后，尾翼张开并赋予炮弹飞行所需的主要升力和稳定力矩。设计尾翼稳定装置时，除了要保证强度可靠外，还需确保尾翼在炮膛内锁定不张开，以防划伤炮管；出炮口后迅速张开到位并被锁定。

制导炮弹的尾翼稳定装置一般有带弹托式，采用惯性块解锁尾翼式，以及利用气缸压力张开尾翼式等几种方式。带弹托式尾翼稳定装置的优点是炮弹在膛内发射时，弹托将尾翼机构包裹，从而能有效减少火药气体带来的烧蚀冲刷作用，提高结构的抗高温、高压和高过载能力。此外按尾翼机构是否被完全包裹又可分为全包式和半包式。美国海军155 mm制导炮弹采用全包式非金属弹托，当炮弹出炮口之后，弹托被炸裂成碎片并散向四周，尾翼随之张开。

国内学者对尾翼的解锁和张开过程做了大量研究，但对带弹托式尾翼稳定装置的研究却并不多见。焦志刚等[1]、蔡灿伟等[2]通过研究气缸压力张开式尾翼机构，分别得到了求解气缸压力变化的数学模型和数值方法。甑文强等[3]、崔二巍等[4]建立了折叠翼展开的数学模型，并对翼的张开和锁紧进行了动力学仿真分析。此外文献[5-7]也采用不同的方法对折叠弹翼的张开过程进行了仿真分析。

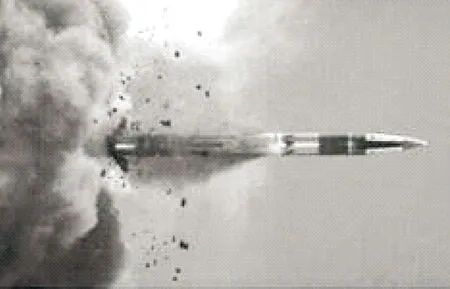
图1 美国海军155 mm制导炮弹出炮口瞬间

文中借鉴气缸式尾翼张开的原理，以某大口径线膛炮为发射平台，设计了一种带金属弹托的半包式尾翼稳定装置。仿真结果表明，炮弹出炮口之后弹托能正常分离，尾翼能够张开到位并被锁定。

1 尾翼稳定装置的设计

尾翼稳定装置模型见图2～图4，它的工作原理是：发射前，弹托将尾翼限位并使之处于折叠状态，弹托与尾翼座之间留有空腔形成气室并由4个螺钉连接(图2)；炮弹在膛内运动时，高压燃气经过弹托上的小孔进入气室，使气室内的压强升高；当炮弹出炮口后，利用气室内外的压强差将螺钉拉断，实现弹托分离；随后尾翼依靠惯性力绕翼轴旋转张开(图3)；张开到位时，销在弹簧力的作用下插入尾翼上的销孔中将其锁定(图4)。

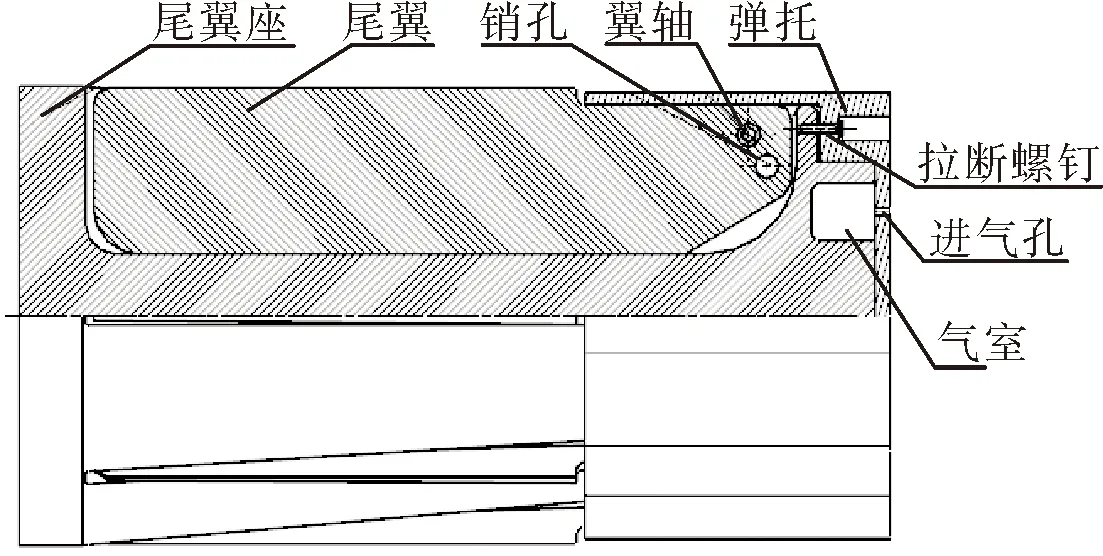
图2 膛内尾翼折叠状态

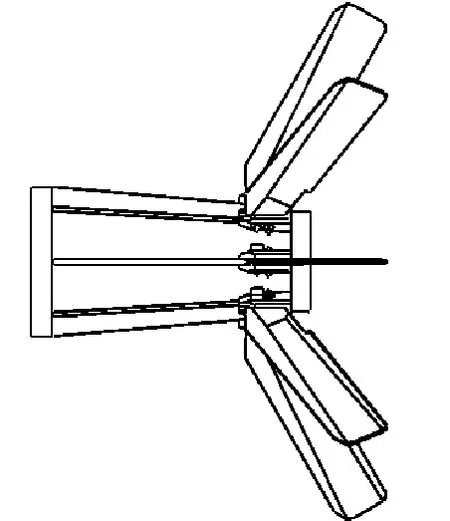
图3 尾翼张开

图4 尾翼锁紧机构

2 弹托分离计算

2.1 气室充放气模型

分析气室内的压力变化规律，实质上是研究气流经小孔的流动问题，通常做以下假设：气体为理想气体；流动过程为定常，且绝热；气室容量相对炮膛较小，气体流入流出气室对膛压的影响可忽略不计[8]。

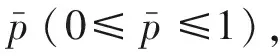
(1)

式中:φ为流量系数，其值与压力及小孔结构有关，一般取0.85～0.95；s0为小孔截面积；γ0为与气体绝热指数γ有关的参量。

(2)

对于膛内火药气体，有：

(3)

式中:R为气体常数;f是火药力(N·m/kg);τ是火药气体温度与火药爆温的相对量，一般取其平均值(约0.8)。将式(2)、式(3)代入式(1)得：

(4)

(5)

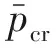
(6)

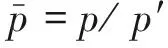
由于气室的容积V是固定的，在时间段dt内有Qdt气体流入或流出，引起的密度变化，进而引起气室内能的变化。由热力学第二定律即可求出气室压力的变化，计算过程及后效期的压力规律详见文献[9]。

2.2 气室压力及弹托分离计算

通过测得的弹丸内弹道离散数据点及气室的参数，采用MATLAB编写计算程序，即可求得气室内压力随时间的变化规律。计算模型气室容积为0.12 L，进气孔直径为3 mm，个数为2，仿真得到的膛压及气室内压力随时间的变化规律见图5。

从图5中可得，在膛内点火发射后，膛压和气室内压力都随时间增大，分别在第14 ms和18 ms时刻达到最大值，之后压力都降低，在27 ms时炮弹出炮口，此后膛压迅速降低至0。整体上表现为气室内压力曲线“滞后”膛压曲线，二者的变化趋势与文献[1-2]中的一致，表明文中计算的正确性。

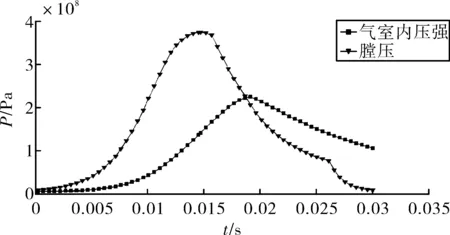
图5 膛压和气室内压力随时间变化规律

设计弹托时，需确保在膛内弹托不分离，即螺钉不被拉断；炮弹出炮口后螺钉被拉断，弹托分离。仅考虑炮弹沿炮管的直线运动，规定炮弹的运动方向为正方向，对弹托进行受力分析，可得：

p·S-p′·S′+F=ma

(7)

式中：S为膛压作用面积；S′为气室内压力作用面积；F为弹托与尾翼座之间的作用力；m为弹托的质量3.0 kg；a为加速度，最大值9 000 g，这里认为a的变化规律与膛压一致。于是得到F随时间的变化关系。

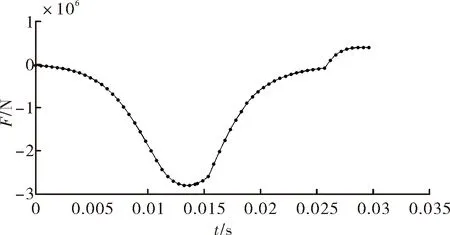
图6 F随时间的变化关系

从图6可得，在膛内(27 ms之内)F<0，即与上述规定的正方向相反，故炮弹在膛内运动时，弹托与尾翼座互相挤压，螺钉不受拉力，因此在膛内弹托不会分离。炮弹出炮口后Fmax=4×105N，其值大于所有螺钉的最大拉力载荷之和，因此炮弹出炮口后，螺钉将被拉断，弹托分离。

2.3 气室参数对气室压力的影响分析

2.3.1 气室容积对气室压力变化的影响

为研究气室容积对气室压力变化的影响，保持进气孔直径3 mm和个数2不变，分别取气室容积为0.04 L、0.12 L、0.2 L和0.8 L，得到气室压力和F变化规律曲线，如图7、图8所示。

由图7可知，在气室容积V由0.04 L增大为0.8 L的过程中，气室内压强随时间增大变慢，压强的最大值减小，气室压力曲线滞后膛压曲线的效果越来越明显。整体上表现为气室容积越小，充气放气越快；气室容积越大，充气放气越慢。

图7 气室容积对气室压力影响的规律曲线

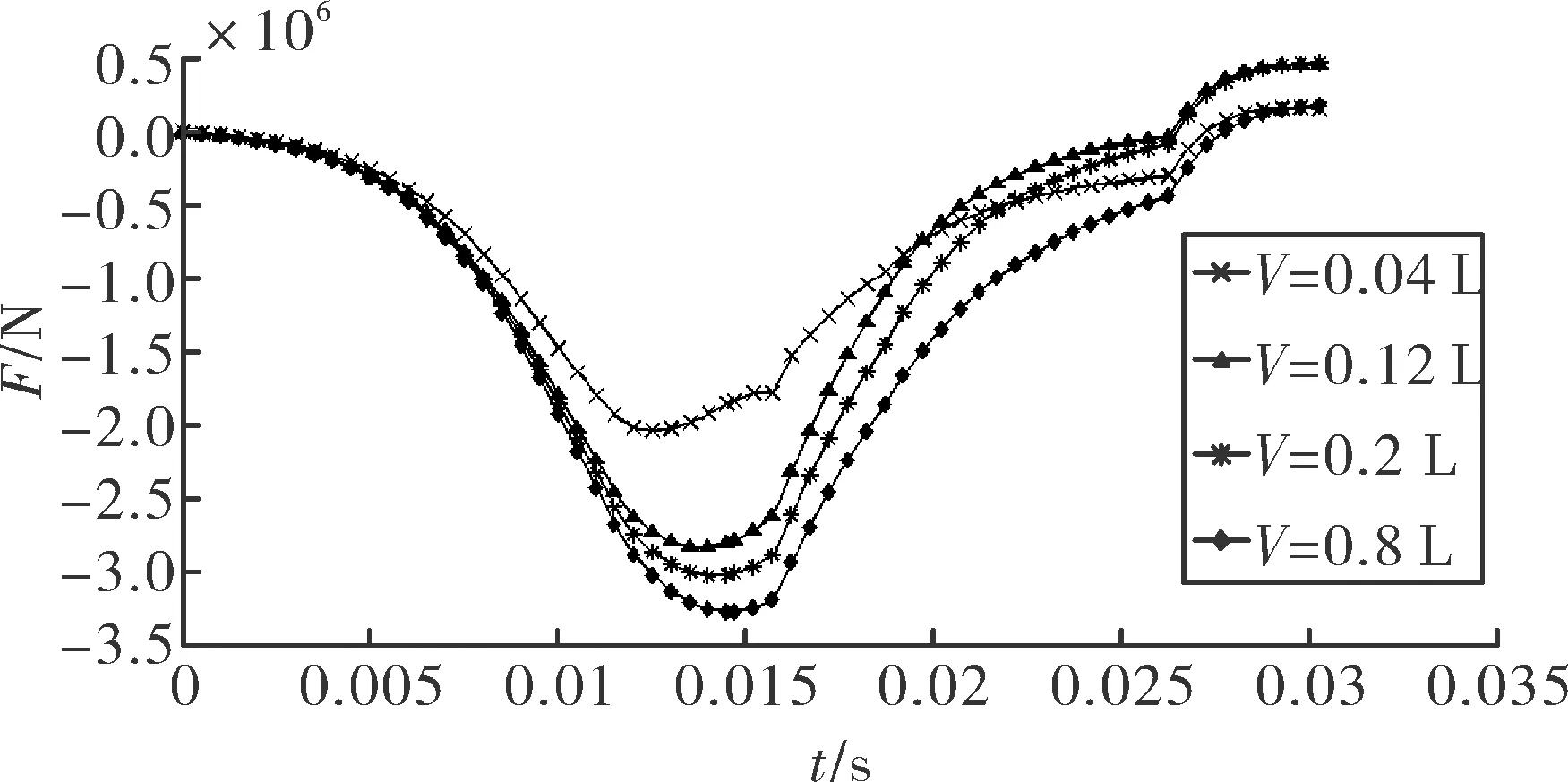
图8 气室容积对F影响的规律曲线

由图8可知，气室取不同的值时，在膛内(27 ms之内)F均为负值，因此弹托不会分离；出炮口后F的值与气室容积的对应关系见下表1。

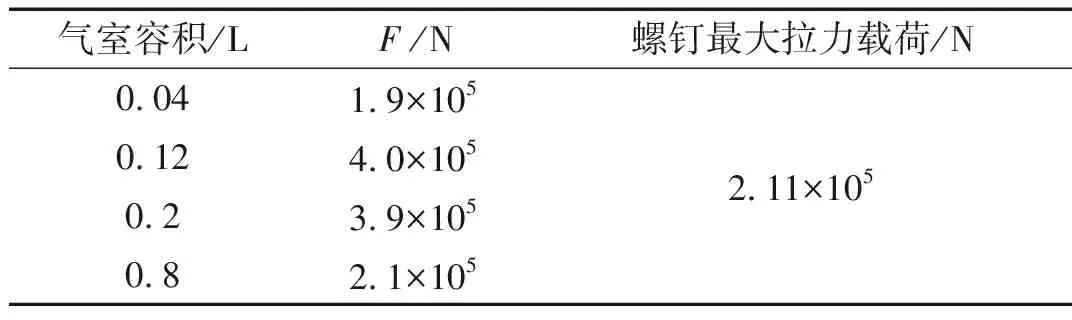
表1 F与气室容积的关系

分析表中数据可知，当V取0.12 L或0.2 L时，出炮口后F的值大于螺钉的最大拉力载荷，即螺钉被拉断，弹托能够分离；反之当V取0.04 L或0.8 L时，出炮口后F小于螺钉的最大拉力载荷，即螺钉不能被拉断，弹托不能分离。

2.3.2 进气孔横截面积对气室压力变化的影响

进气孔横截面积由进气孔的个数和单个孔的直径来决定。为研究进气孔横截面积对气室压力变化的影响，保持气室容积V=0.12 L不变，这里进气孔个数取为2，单个进气孔的直径分别取为0.8 mm、3 mm、3.6 mm和6 mm，得到气室压力和F变化规律曲线，如图9、图10所示。

由图9可知，在进气孔直径d由0.8 mm增大为6 mm的过程中，气室内压强随时间增大变快，压强的最大值增大，气室压力曲线滞后膛压曲线的效果越来越不明显。整体上表现为进气孔直径越大，气室充气放气越快；进气孔直径越小，充气放气越慢。

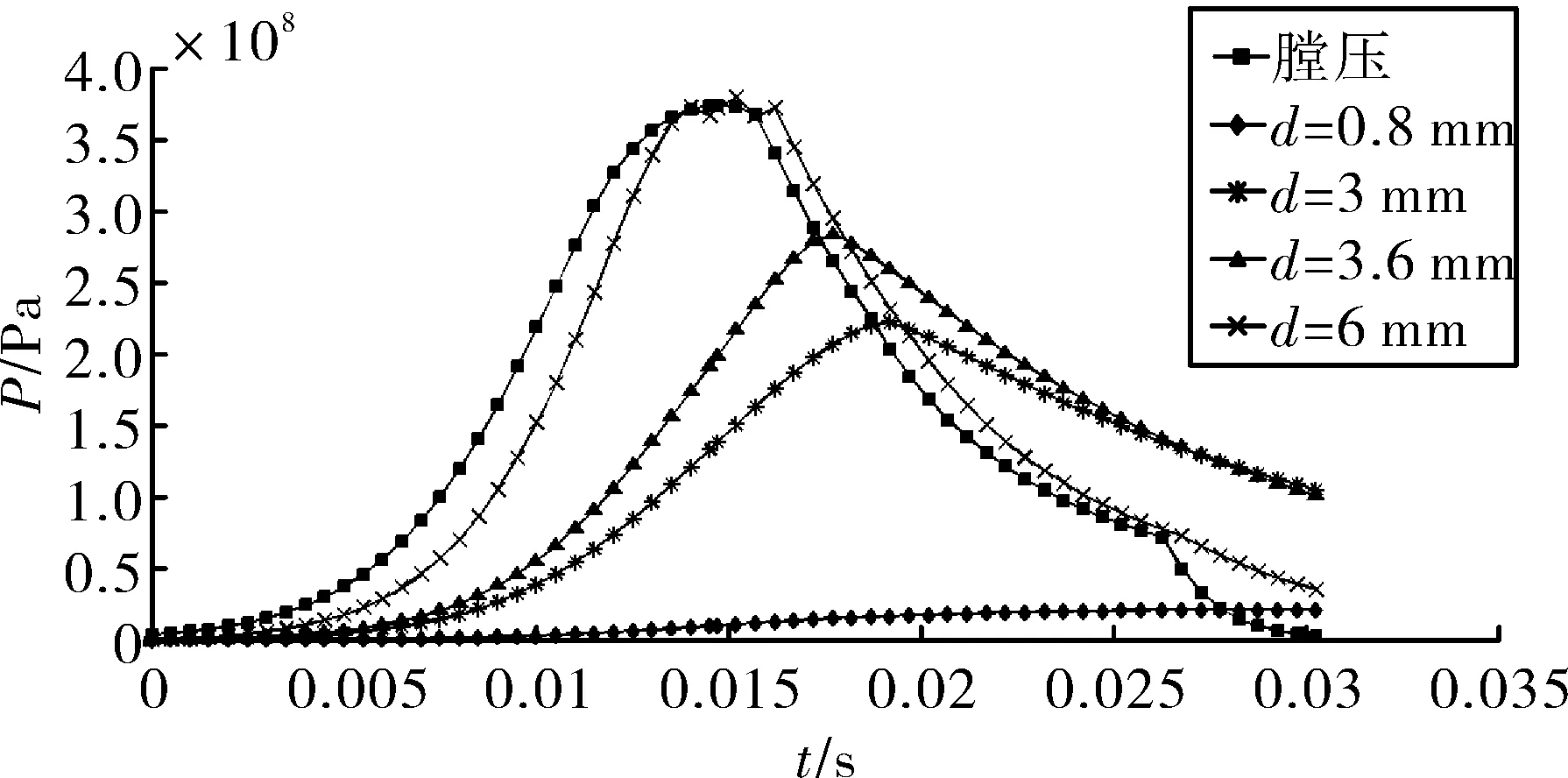
图9 进气孔直径对气室压力影响的规律曲线

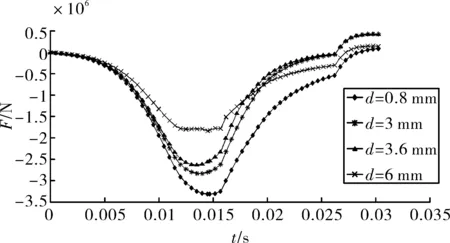
图10 进气孔直径对F影响的规律曲线

由图10可知，进气孔直径取不同的值时，在膛内(27 ms之内)F均为负值，因此弹托不会分离；出炮口后F的值与进气孔直径的对应关系见表2。

表2 F与进气孔直径的关系

通过分析表中数据可知，当d取3 mm或3.6 mm时，出炮口后F的值大于螺钉的最大拉力载荷，即螺钉被拉断，弹托能够分离；反之当d取0.8 mm或6 mm时，出炮口后F小于螺钉的最大拉力载荷，即螺钉不能被拉断，弹托不能分离。

综上，在确定火炮和发射药号的前提下，气室容积以及进气孔横截面积太大或太小，都可能导致出炮口后连接螺钉不能被拉断，弹托不能分离，造成发射失败。因此合理地设计气室容积的大小，进气孔的个数和直径以及它们之间的匹配关系就显得尤为重要了。

3 尾翼张开动力学仿真分析

尾翼张开性能关系着炮弹发射后能否正常飞行，是设计尾翼的重要指标，主要包括张开速度快、一致性好、锁死不回弹[4]等。

3.1 动力学模型的建立及仿真

基于Adams多体动力学分析软件，设定初始条件，并依据尾翼张开和锁紧的原理，添加相应的约束和运动副[3]，建立尾翼张开和锁紧过程的动力学仿真模型。

将惯性系炮弹作为参考系，对尾翼张开过程进行受力分析，可以得到以下关系式：

(8)

式中:M1、M2、M3分别为尾翼座、销、翼轴对尾翼的摩擦力矩，T为气动力矩，R为炮口处火药力对尾翼的力矩，J为尾翼绕翼轴的转动惯量。以线膛炮为平台发射的弹丸出炮口后具有一定的转速，仿真条件为转速20 r/s；锁紧簧的预紧力58.9 N，刚度6 200 N/m；销与尾翼之间动摩擦因素0.1，忽略气动力及炮口火药力作用的影响，得到的仿真结果如图11～图13。

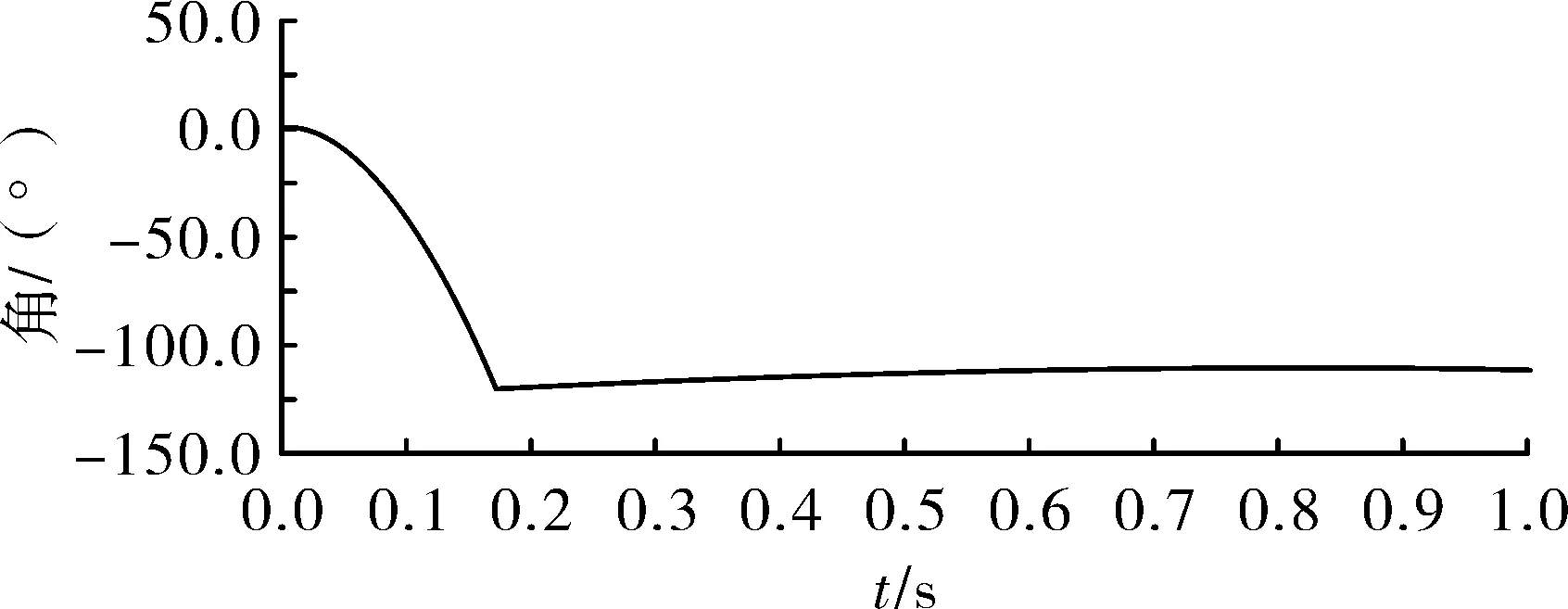
图11 尾翼张开角度随时间变化曲线

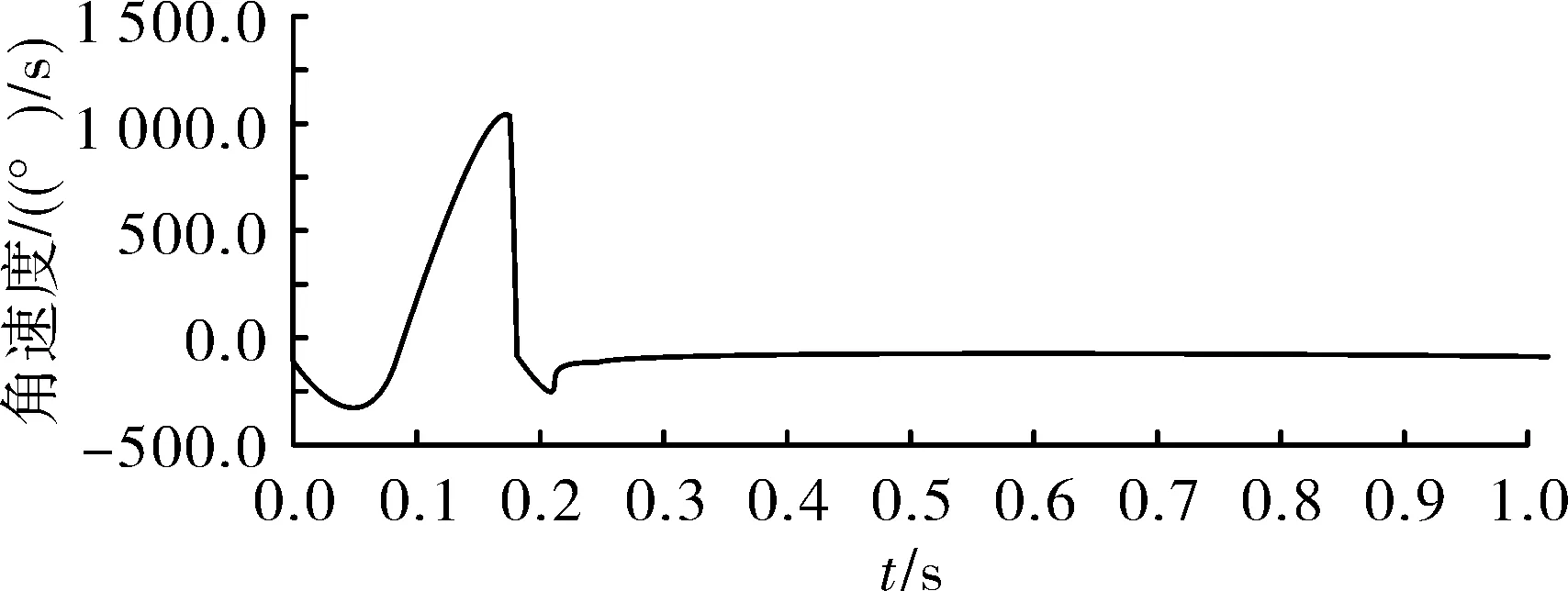
图12 尾翼张开角速度随时间变化曲线

图13 尾翼与销接触力曲线

由图11～图13得知，尾翼质心绕转轴转动了120°，这与理论上前折后张并后掠30°的尾翼应转过的角度保持一致；尾翼绕转轴转动的角速度逐渐增大，最大值为3 r/s，在0.2 s处急剧减为0，即尾翼不再绕转轴转动；开始仿真后，尾翼与销之间的接触力保持为一个较小的值，这是尾翼与销之间的滑动摩擦力，在0.2 s处附近接触力急剧增大到峰值为362 N，之后迅速减小为0，表明此时锁紧销已经插入到尾翼上的销孔中并将其锁定。综上分析，此尾翼稳定装置在当前的仿真计算条件下，尾翼能够正常张开并被锁定。

3.2 转速对尾翼张开的影响

工程经验表明，在忽略气动力和炮口火药力作用影响的前提下，出炮口后影响尾翼张开的最主要因素是弹体的转速。基于上述仿真计算的条件，这里分别仿真弹体转速为15 r/s、18 r/s、20 r/s尾翼的张开过程，保持锁紧簧刚度6 200 N/m，销与尾翼之间动摩擦因数0.1不变，仿真结果见图14～图16。

图14 不同转速下尾翼张开角度随时间变化曲线

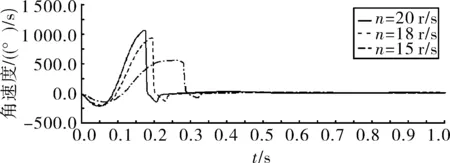
图15 不同转速下尾翼张开角速度随时间变化曲线

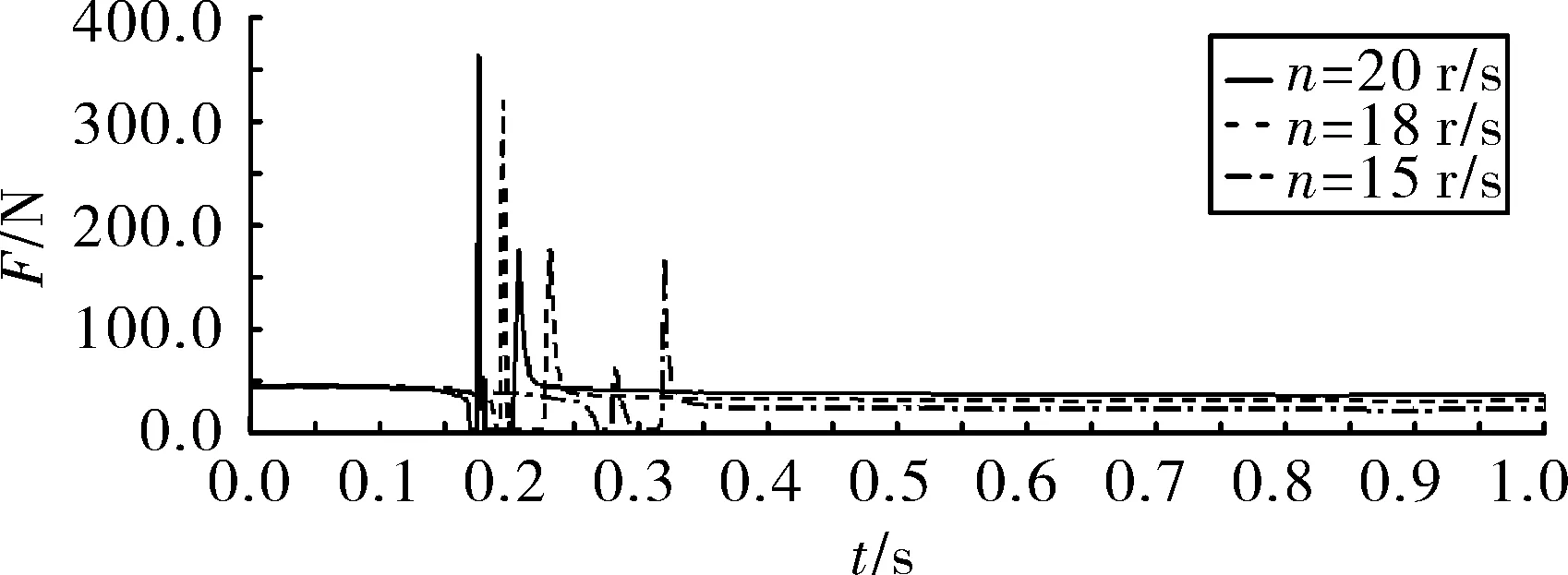
图16 不同转速下尾翼与销接触力曲线

由图14～图16可以得出，对应转速为15 r/s、18 r/s、20 r/s，尾翼张开转过的角度均为120°，尾翼与销接触力最大值分别为168 N、317 N、362 N，锁紧所用时间分别为0.32 s、0.23 s、0.2 s，3种转速下尾翼均能被锁定。因此弹体转速的大小显著地影响着尾翼张开的快慢，随着转速的增加，尾翼张开加快，张开时间减小，锁紧时尾翼与销接触力增大，因而对销的抗剪强度要求也相应的提高。此外，影响尾翼张开过程的因素还有锁紧簧预紧力、锁紧簧刚度、尾翼和销之间的动摩擦因素以及尾翼和尾翼座之间的配合间隙等，有待进一步深入探讨。

4 结论

文中以某大口径线膛炮为发射平台，借鉴气缸式尾翼张开的原理，设计了一种带金属弹托的半包式尾翼稳定装置，在阐述了此尾翼稳定装置工作原理的基础上，建立了气室充放气模型和尾翼张开锁紧的动力学仿真模型，并分析了影响弹托分离和尾翼张开的因素，得到以下结论：

1)文中设计的尾翼稳定装置在炮弹出炮口之后弹托能正常分离，尾翼能够张开到位并被锁定；

2)气室容积和进气孔横截面积的大小以及它们之间的匹配关系将决定弹托能否分离；

3)弹体的炮口转速显著地影响着尾翼的张开及锁紧性能；

4)文中的工作可为尾翼稳定装置的设计提供一种新的思路。