战术级捷联惯导方位装订的半自主对准*

崔 潇，秦永元，杨小康，梅春波

(1 西北工业大学自动化学院， 西安 710129； 2 西安现代控制技术研究所, 西安 710065)

0 引言

常规火箭弹采用捷联惯导进行制导改造后，可显著增加有效射程、打击精度大幅提高，制导火箭弹在世界各国得到了广泛的应用，成为火箭弹发展的主要趋势[1-2]。

由于战术条件和弹载捷联惯导自身器件精度的限制，火箭弹无法单纯依靠自身完成初始对准，一种方案可采用依靠发射车装备的高精度惯导进行传递对准[3]，但是需要发射架进行俯仰、回转机动，对准精度也受到时空同步等因素影响；另一种方案采用方位装订，以速度+方位为量测的卡尔曼滤波对准方案[4]。两种对准方案均涉及滤波器设计，存在收敛时间长以及受初始条件参数影响等影响。因此，研究基于方位装订的捷联惯导快速初始对准具有较大工程应用价值。

1 坐标系定义

为便于分析，定义如下坐标系：

1)弹体坐标系b：原点位于弹体质心，xb、yb、zb分别为沿弹体的前、上、右，xbybzb构成右手直角坐标系；

2)当地水平坐标系H：原点位于弹体所在点，xH为xb在当地水平面内的投影，zH沿当地地垂线，向上为正，yH与xH、zH构成右手坐标系。

3)当地地理坐标系g：原点位于载体所在点，yg轴沿地理垂线指向上，xg、zg轴在当地水平面内且xg沿当地经线方向指向北，zg沿当地纬线切线方向指向东，即“北天东”地理坐标系。

2 水平自对准

2.1 水平姿态矩阵

设对准时刻导弹的航向角为ψ(北偏东为正)，俯仰角为θ，横滚角为γ，则:

(1)

(2)

图1 地理坐标系与载体坐标系转换关系图

(3)

2.2 T2周期内的水平姿态四元数计算

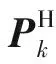
tk=kT2=kNT1

(4)

上述时间周期关系如图2所示。

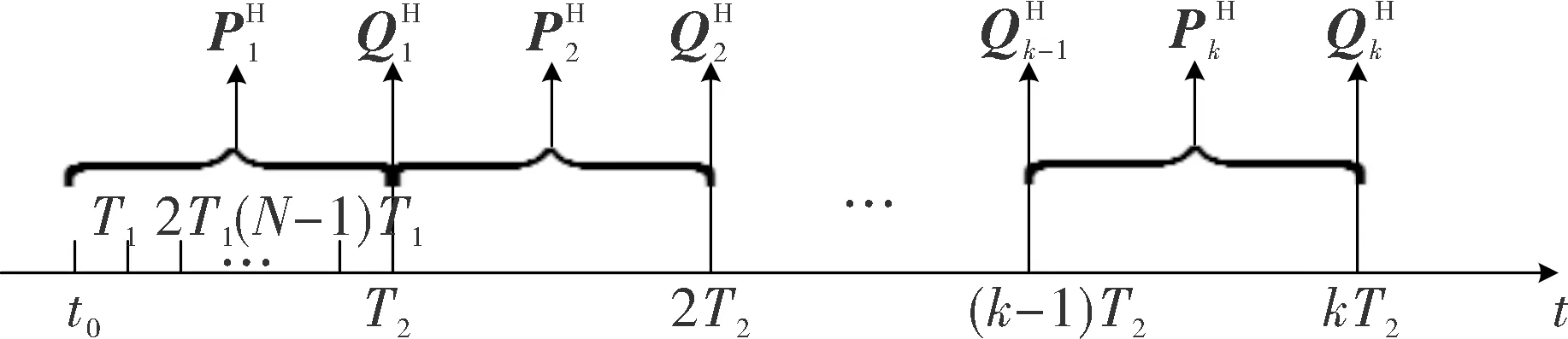
图2 T1周期、T2周期、水平姿态四元数间的关系

忽略弹体晃动，则加速度计输出为：

(5)

即

(6)

假设加速度计输出经过I-F变换。记在第k个T2周期内，第n个T1周期内的加速度计输出积分为δVxk(n)，δVyk(n)，δVzk(n)，即有：

(7)

则在第k个T2周期内加速度计输出的积分为：

ΔVxk=NT1gsinθ=T2gsinθ

(8a)

ΔVyk=NT1gcosγcosθ=T2gcosγcosθ

(8b)

ΔVzk=-NT1gsinγcosθ=-T2gsinγcosθ

(8c)

记

(9)

由于加速度计存在测量误差，弹体存在晃动干扰，所以gk≈g·T2。

记

(10)

则由式(10)得：

(11a)

(11b)

(11c)

(11d)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

由式(19)、式(21)、式(23)得：

(27)

2.3 tk时刻的水平姿态四元数计算

(28)

2.4 引入外基准航向后的姿态四元数

设tk=kT2=kNT1时刻水平对准结束，外基准引入的航向角为ψ，则与ψ对应的四元数为：

(29)

由于

(30)

根据姿态阵的矩阵乘与四元数乘之间的关系，得与式(29)对应的姿态四元数为：

(31)

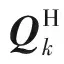
3 陀螺漂移估计

考虑如下四元数更新离散方程：

(32)

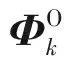
由文献[5]已知：

(33)

则

(34)

式中:Δθx、Δθy、Δθz为在[tk,tk+1]时间间隔内的角增量。

假设陀螺输出为：

(35)

记

(36)

则误差转移矩阵ΔΦk可以表示为一个矩阵幂级数，幂级数第n项为Ο(‖δωkΔt‖n) ，如果只考虑一阶近似，则:

ΔΦk≈M(δωk)Δt

(37)

式中:

(38)

将式(36)、式(37)代入式(32)，可得:

Qk+1=ΦkQk-ΔtM(δωk)Qk

(39)

定义矩阵:

(40)

则容易得:

M(δωk)Qk=Ξ(Q)δωk

(41)

则式(39)可写为:

(42)

式中：wk为四元数更新误差，是陀螺测量误差的函数。

对于战术级惯导，陀螺启动常值漂移很大，若仅仅考虑陀螺仪的常值漂移δωk≈εb，则可得：

(43)

4 仿真分析

为进一步检验文中所提的半自对准方法的性能，进行了摇摆基座下对准的仿真。

4.1 仿真条件

1)弹体绕俯仰轴、横滚轴和方位轴的摇摆运动，可看作由一系列幅值和频率相近的正弦波来描述：

(44)

式中：θ、γ、φ分别为绕俯仰轴、横滚轴和方位轴的摇摆角度；θm、γm、φm分别为摇摆角度幅值；ωθ、ωγ、ωφ为摇摆的角频率；θ0、γ0、φ0为摇摆的初始相位。

表1 摇摆参数设置

2)惯导参数设置：

表2 惯导参数设置

3)惯导采样周期：0.01 s(即T1)；T2=0.1 s。

4.2 仿真结果

根据4.1设置的仿真条件，仿真结果如图3～图5所示。

图4 摇摆基座对准估计结果(不同陀螺常值漂移)

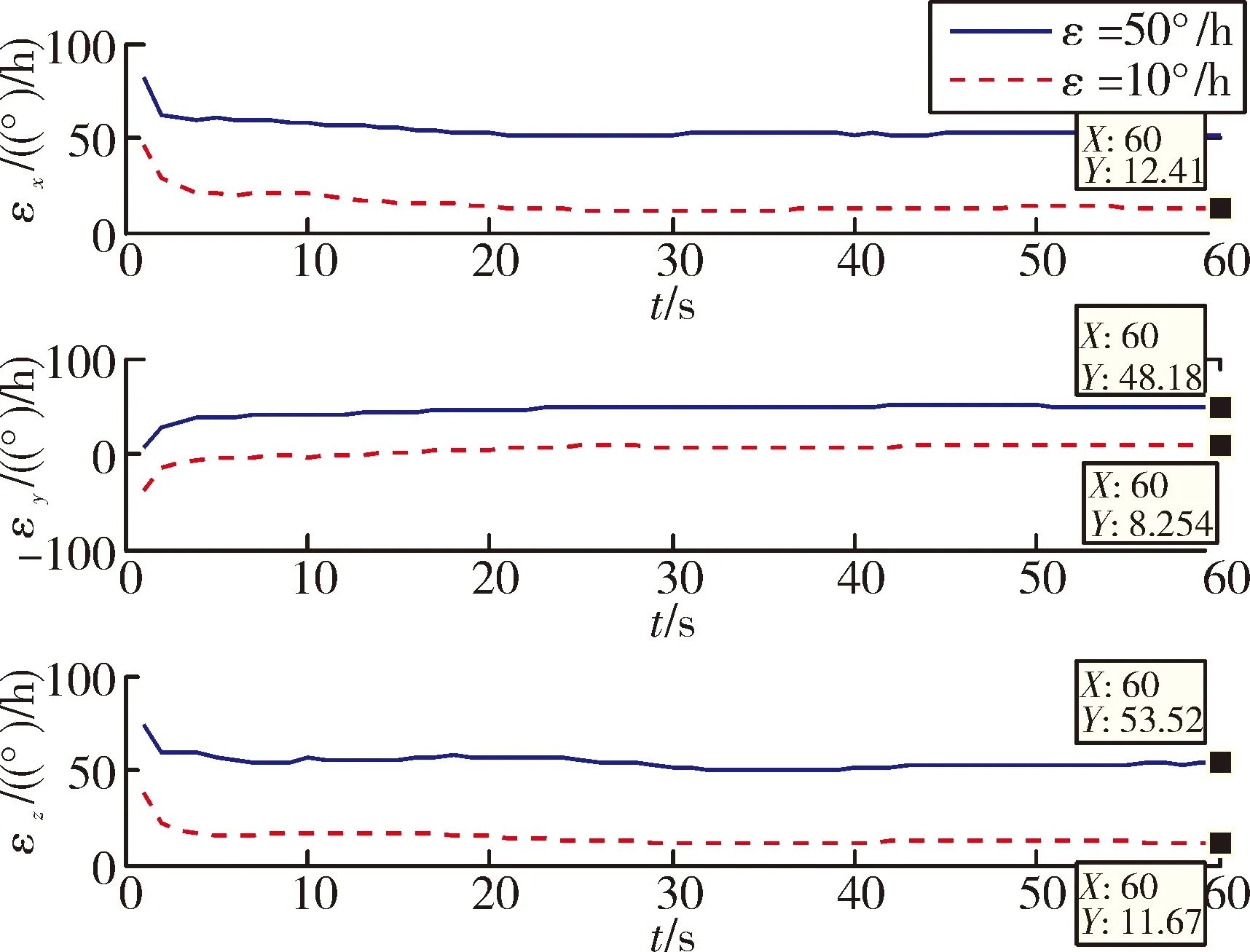
图5 陀螺漂移估计结果(T2=0.1 s)

图3中实线表示真实姿态曲线，虚线表示对准结果，从图3中可以看出，由于航向角由外部装订，基本无误差，水平自对准姿态可以跟踪真实姿态，只是存在时间延迟，对比不同T2的结果，T2周期越大，造成的延迟也越大，所以，实际工程中，根据加速度噪声大小、弹体晃动幅度及频率等因素，适当调整T2周期。

为了验证不同陀螺常值漂移对算法的影响，图4给出了不同陀螺漂移下的对准结果，从图4中可知，陀螺常值漂移不影响水平对准结果，结果和前面的分析一致。图5给出了在同一更新周期T2下对陀螺漂移的估计结果，可知算法可以对陀螺常值漂移进行粗略估计，估计精度且与漂移大小无关。

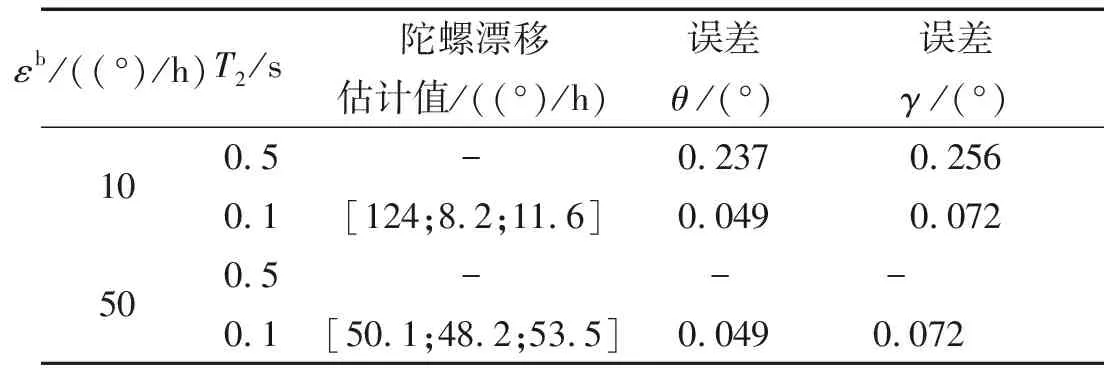
表3 对准结果统计

表3总结了对准结束时刻的对准精度。从表3中可知，减小更新周期T2对准精度也随之提高，当T2=0.1 s时，对准精度在0.1°以内，而陀螺常值漂移大小不影响姿态对准结果。

5 结论

仿真结果表明：文中给出的战术级捷联惯导方位装订的半自主对准方法在对准的同时，还可对陀螺常值漂移进行粗略估计，但加速度计零偏无法得到估计。与传统基于卡尔曼滤波对准方法相比，文中的方法具有运算简单、计算量小和便于工程应用的优点，为火箭弹的对准提供了参考。