水下探测直升机噪声衰减规律的研究*

王显强，任 波，李天姣

(沈阳理工大学装备工程学院， 沈阳 110159 )

0 引言

在现代战争中，直升机凭借其低空、超低空的优势，能有效地探测到潜艇，对潜艇有着致命的威胁。面对直升机这一威胁，虽然防空导弹系统基本已经成熟，但是要全部装备潜艇，我国还有很长的路要走，而且我国海岸线较长，领海大部分是深度小于600 m的浅海区域，而浅海的深度不利于潜艇的隐蔽。

直升机在海面上侦查时低空飞行且速度慢，甚至是悬停在海面上。这时潜艇在水下就可以通过对直升机噪声信号的探测识别来有效地打击直升机。潜艇要想在水中利用接收到的直升机噪声信号先一步探测和识别空中的目标，就要先了解直升机噪声信号从空气中传播到海水中的衰减规律，这样就能更简便迅速的探测识别信号。

1 建立直升机噪声声源

低频声波可以在浅海进行远距离的传播。而直升机噪声频率范围一般在10～80 Hz[1]，是一种低频声波，且其主旋冀旋转噪声的基频能量较强，其线谱能量一般在16～180 dB。

直升机的噪声声源可以看做是点声源，波面为球面波，噪声基频可以用瞬态震源来模拟。瞬态震源可以近似的看做围绕一个固定主频左右包含了一定频率范围的脉冲信号。采用雷克子波模拟瞬态脉冲式震源，其表达式为:

F1(t)=A·[1-2·(π·f)2(t-t0)2]·e-(π·f)2(t-t0)2

(1)

式中：A为幅值;f为主频;t0为时移。

取A=1，f=80 Hz，则震源如图1、图2所示。

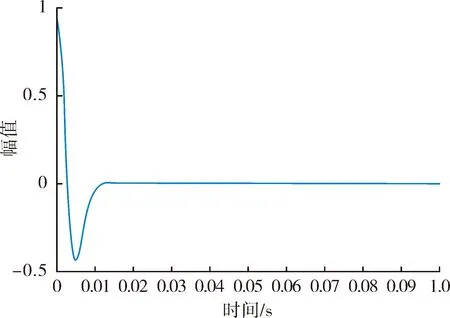
图1 瞬态震源时域图

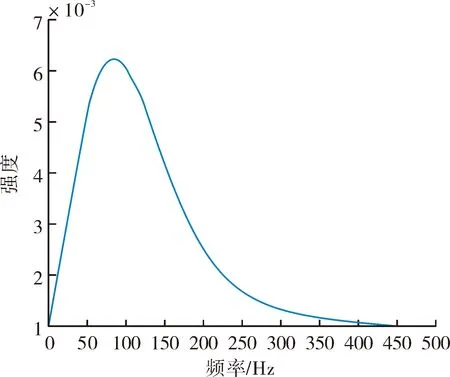
图2 瞬态震源频域图

2 建立直升机噪声传播模型[2]

反潜直升机在海面进行反潜活动时，一般距离海面10～50 m。用有限元方法建立模型时，声源高度为10～50 m，海水深度为600 m。由于声源和空气、海水模型有对称性，可以建立四分之一模型。对于远海区域部分和海底，可以将模型边界面设置为无反射边界条件，空气和海水的接触面设为自然接触。采用雷克子波模拟的瞬态脉冲式震源作为声源，施加于空气模型上表面的任一顶点，作为点声源。所建部分模型如图3、图4所示。

图3 声源距离海面为10 m的模型

图4 声源距离海面为50 m的模型

3 声波在空气中的传播规律

直升机噪声源距海面为h，声呐距海面为d，直升机水平距离为r，设空气的密度为ρa=1.25 kg/m3，空气中的声速为ca=334.0 m/s，海水的密度为ρw=1 000 kg/m3，海水中的声速为cw=1 500 m/s，声波的入射角为θi，反射角为θr，透射角为θt，入射波声压为pi，反射波声压为pr，透射波声压为pt，海水与空气密度之比m=ρw/ρa，空气与海水中的声速之比n=ca/cw，如图5。

图5 声波水空界面传播示意图

点声源在空气中以球面波的形式传播，球面波的能量流在没有损耗时，是随着离开声源距离的平方成反比例地减少，由于粘性的损耗引起了另外的衰减。点声源在r处的声强或通过单位面积的平均功率[3-4]为：

(2)

球面声波的声强为：

(3)

用有限元的方法，建立直升机噪声在空气和海水的传播模型，并进行仿真分析。图6是球面波在空气中传播了0.1 s时的纵截面图，波形为半圆形。图7是球面波到达水空界面时，在界面处的传播图，波形为向外扩散传播的同心圆。

图6 0.1 s时点声源在空气中传播

图7 0.17 s时球面波在水空界面处传播

图8 0.17 s时声波折射到水面平面图

图9 0.17 s时声波传播纵面图

球面波传播到水空界面时，部分声波会透过水空界面进入到海水中，其余的则被反射回空气中。比较图7和图8，可以明显看出声波在水空界面处有能量损耗。透射进入海水的声波则在海水中继续传播，如图9所示。

4 声波在水空界面的衰减规律

声波在传播时，不仅受到几何扩散带来的能量衰减，同时还受到界面耗散的衰减作用。设R为声波反射系数，V为声波折射系数，对平面波在海水与空气中的传播规律[3-4]研究得到:

(4)

假定入射波声压振幅为1。则：入射声波声强Ii=(2ρaca)-1，反射声波声强Ir=R2(2ρaca)-1，折射声波声强It=V2(2ρwcw)-1。当声波垂直入射到海面时，则式(4)的反射系数、折射系数可简化为：

(5)

介质分界面能量传播规律为：

(6)

将海水和空气密度及声速比例系数代入式(6)可得：

It=1.1×10-3Ii≈10-3Ii

(7)

由式(7)可知，当空气中目标辐射噪声由空气向海水垂直入射时，只有约1/100 0的能量能够穿过空气与海水界面传播到海水中[5]。由噪声级数学模型SL=170.8+10lg(I·S)+DI(S为入射声波所覆盖的面积)得：

SLt=170.8+10lg10-3Ii·S+DI=

170.8+10lgIi·S-30+DI=SLi-30

式中：SLi和SLt分别为声波的入射噪声级和折射噪声级。声波从空中垂直传播到海水的过程中噪声级传播损失大约为30 dB。

图8是点声源距离海面10 m处，声波在空气和海水中传播的能量衰减曲线。在0.026 s左右的时候，空气中的声波到达水空界面，陆续到达水空界面的球面波经过界面的反射和折射，最后大约有千分之一的能量通过水空界面折射进入海水中，其余大部分的能量则被折射回了空气中。

图9是点声源距离海面50 m处时，声波传播时能量衰减曲线。声波在0.15 s左右时到达海面，球面波经过水空界面时，大部分的能量被折射回空气中，大约有千分之一的能量透射进入了海水中。

从总能量来看，球面波在经过水空界面后，只有千分之一的能量会进入到海水中，噪声级能量损失为30 dB。

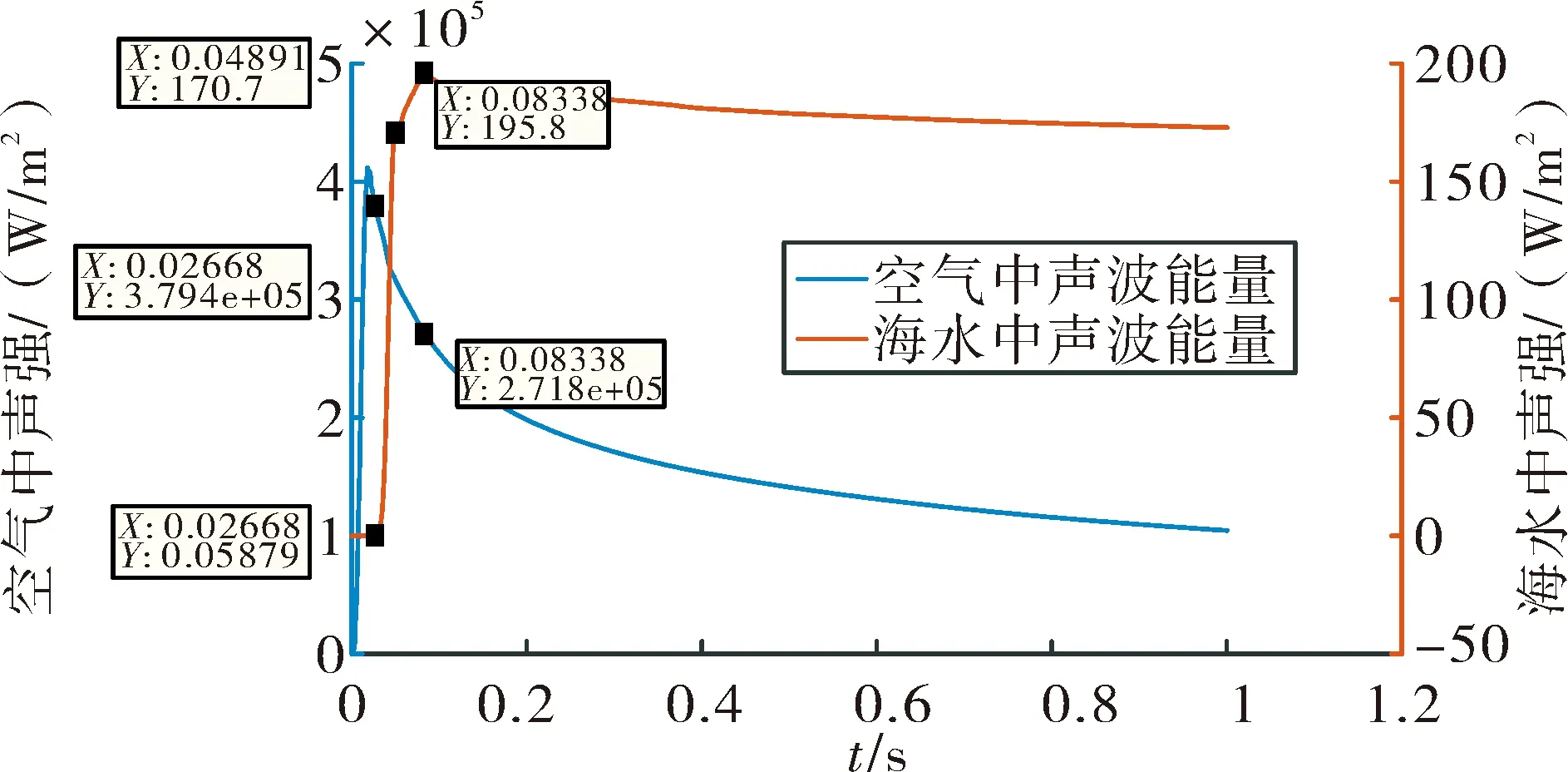
图10 空气和海水中声强变化

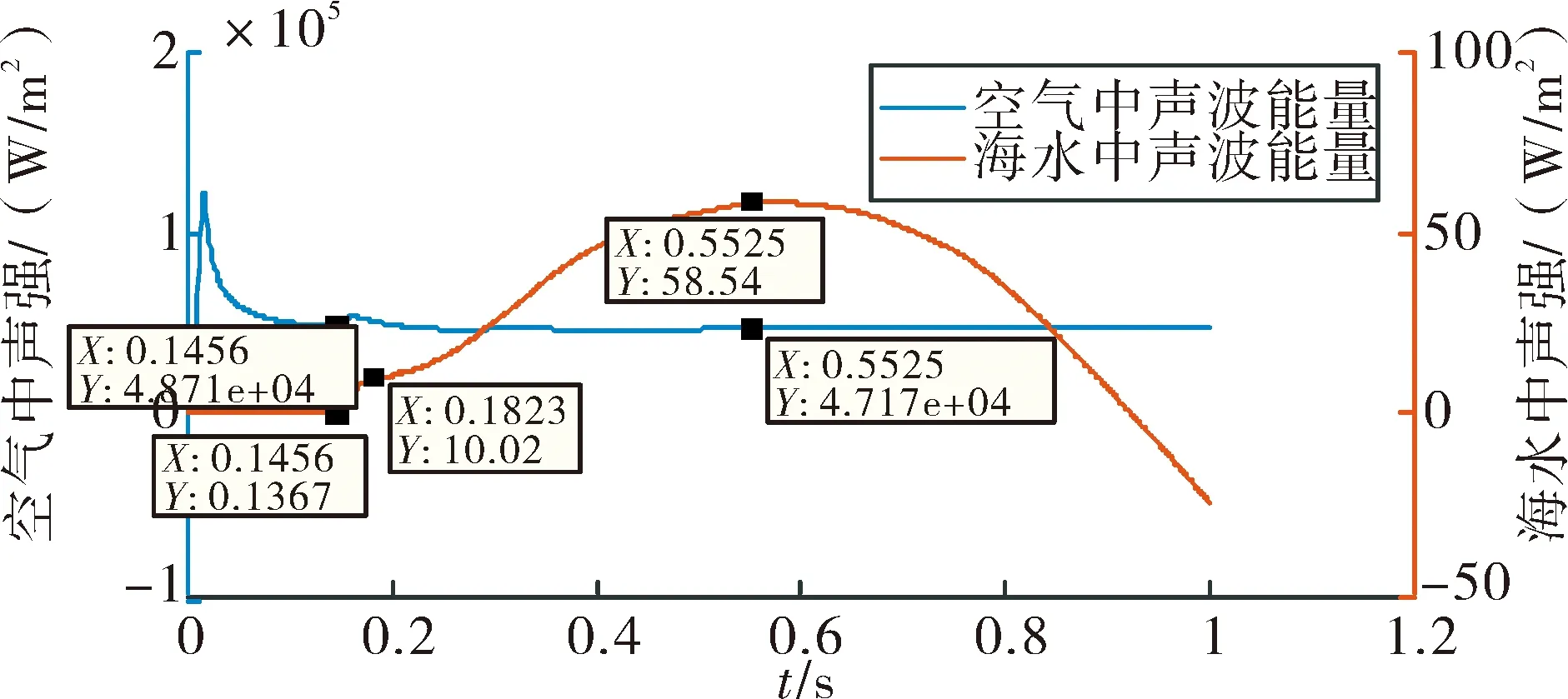
图11 空气和海水中声强变化

平面波的透射临界角为12.8°，也就是说平面波入射角小于临界角时，平面波才能有部分声波透射进入海水中；当入射角大于临界角时，声波会发生全反射，全部被折射回空气中。

球面波的波面是球面，当球面波传播到海面时，如果把某一单位面积的球面波看成是几个平面波的叠加，那么这些叠加的平面波总会与海面存在夹角。根据平面波在水空界面衰减规律，球面波入射角度越大，与海面的夹角越大，其能量衰减的就越多。

声源正下方垂直入射的能量如图12和图13所示。图12表示的是空气中声波垂直入射时能量，垂直入射点能量大约为1.66×102W/m2。图13是垂直入射的声波透射进海水时的能量,垂直透射点能量大约为7.867×10-2W/m2。透射时大约损耗了30 dB的噪声级能量。

图14和图15分别是在水空界面两侧水平距离垂直入射点50 m、80 m、100 m处取得的6个点的能量变化曲线。在50 m处，能量比值为1.5×104；在80 m处的能量比值为1.7×104；在100 m处的能量比值为5.2×104。所以在球面波传播所覆盖的半径为100 m的圆面内，任意某一点声波透射界面时能量损失大约在30～50 dB。

图12 声波垂直入射空气中能量

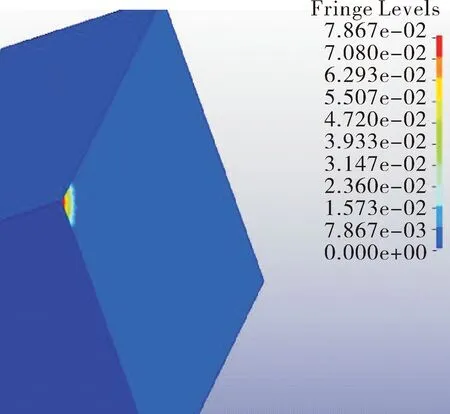
图13 声波垂直透射海水中能量

图14 水空界面附近空气声强变化

5 声波在海水中的传播规律

直升机噪声部分声波会透过水空界面进入到海水中，并在海水中传播。用有限元的方法建立声源距离水面50 m的模型并进行仿真，其结果如图16、图17所示。

图16表示的是0.26 s时声波在海水中传播情况。由于球面波的波面为球面，到达水空界面的时间不同，水平距离不一样，所以声波先后折射进入海水中，在海水中声波以一种弧形面传播。图17所示的是0.52 s的时候声波传播的纵截面图。可以看出有部分声波将要传播到海底了。

图16 0.26 s时声波在海水中传播

图17 0.52 s时声波在海水中传播

低频声波在浅海具有良好的传播特性，假定在浅海短距离内声波传播时，海洋介质参数基本不变。根据射线声学的理论，声波在水中的声场公式[3]为：

(8)

式中：pq为声呐处的声压;p为距离点声源单位距离处的声压。因为推导衰减公式时，不仅忽略了环境因素，而且还进行了近似取值，但其所得出的衰减规律跟仿真出的声波在海水中的衰减规律相吻合。并且仿真得出的衰减规律，跟用简正波法求解出的声波在海水中的衰减规律也相符合。

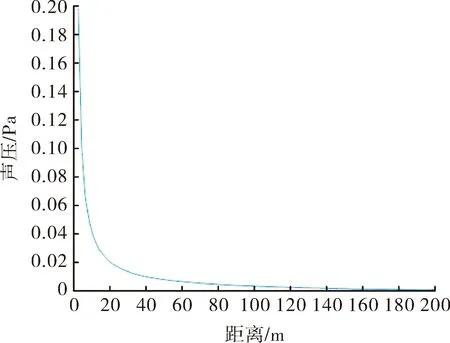
图18 公式曲线

图19 仿真曲线

6 结束语

反潜直升机由于其探测设备的原因，直升机在探测潜艇时需要尽可能的接近海面，有时甚至近距离悬停在海面上。近距离的直升机噪声为潜艇探测识别到直升机提供了优势。在浅海区域，当直升机噪声信号通过水空界面时，透射面积大，大约有千分之一的总能量能够透射进海水中，其噪声能量级衰减了30 dB。能量的衰减跟声波入射角度成正比，声波入射角越大，能量损失的就越多。通过水空界面，透射进来的声波可以传播到浅海海底，传播范围较大，潜艇在一定距离内可以用声呐等设备对该信号进行探测，来识别空中的直升机，实现对直升机的反潜。