基于转移自洽和偏好连接的链路预测算法研究

陆圣宇，史 军，刘 宝，姚金魁，金 毅

(江南计算技术研究所，江苏 无锡 214083)

0 引 言

复杂网络从宏观角度分析，是具备自组织、自相似、小世界、无标度中部分或全部性质的网络。近年来，复杂网络不仅仅作为数据的表现形式，更代表着数据科学、网络科学的主要研究方向，基于数据的复杂系统的数学模型正以一种全新的视角快速发展[1]。许多复杂系统都可以抽象成一种复杂网络进行分析，比如常见的电力网络、航空网络、交通网络、计算机网络以及社交网络等，其研究价值日益凸显。

链路预测[2]是复杂网络中的高效建模分析方法，通过基于网络节点的属性信息和网络拓扑结构信息而展开。链路预测主要有两个研究方向[3]，一是对客观存在但仍然未知的网络拓扑链路进行预测，二是对未来将要发生连接关系的网络拓扑链路进行预测。

作为数据挖掘领域的研究模式之一，早期链路预测重点倾向于基于机器学习、马尔可夫链[4]等方向。这些通过获取节点属性等外部信息来建立起高效预测优势，例如综合网络拓扑结构信息与网络节点属性开展预测，或者通过对节点属性定义节点对的相似性程度开展预测。但在多数情况下，对节点属性信息的获取存在明显困难[2]。因此，在不使用节点属性信息的前提下，通过获取纯粹的网络结构信息来定义相似性指标，成为当前链路预测的一种主流方法。其核心在于选择定义网络中节点间的相似性度量指标，一个重要假设前提就是两个节点之间相似性越大，相应两个节点之间存在链接的可能性就越大[5]。

在其他的链路预测算法中，当前主要有基于似然分析的方法和机器学习方法。在基于似然分析的方法中，有通过族谱树进行网络层次划分的层次结构模型[6]，将节点聚类组成集合进行预测的连边的随机分块模型[7]和根据网络中封闭回路数定义网络似然的闭路模型[8]。在机器学习方法中，针对链路预测主要有基于特征分类、概率图模型和矩阵分类[9]，都是需要有监督的机器学习方法。

文中重点从节点度数和相似性传递的角度分析二者在链路预测过程中的影响，将基于节点度数的偏好连接相似性矩阵作为转移自洽相似性指标的直接相似性输入，通过矩阵求逆的方式求解对应的转移相似性，并通过调节直接相似性与转移相似性比例参数ε，优化最终链路预测结果的AUC值。然后就基于网络结构相似性的指标算法进行简要介绍；通过比较算法的特性，从基于偏好连接相似性和转移自洽相似性指标出发，构造TSPA相似性指标算法；最后结合经典复杂网络数据集进行对比分析实验。

1 基于结构相似性的链路预测指标

基于结构相似性的指标代表了通过节点之间的结构信息(例如节点的度、最近邻居、二阶邻居等)进行加权计算获得的相似性指标。当计算得到的相似性指标越大，那么该节点对之间产生连边的概率也越大。当前大部分基于结构相似性的链路预测相似度都从共同邻居算法的思想出发，其主要优点是共同邻居信息的获取较为容易且计算复杂度低。

1.1 CN指标

在基于共同邻居的相似性指标集合中，CN指标(common neighbors)最早来自于Lorrain等[10]提出的社交网络中的个体结构等价性，通过观察，如果特定的节点对所共有或共享的外部节点数量较多，则判断特定节点对之间存在高度的同质性。Kossinets[11]在社交网络的分析研究中发现，共同朋友越多的人成为好友的潜在可能性越大。Newman[12]同样在科学家合作网络中发现，存在更多共同的第三方科研合作者的科学家之间，在未来进行同一科研合作项目的可能性更大。

CN指标如下：

suv=|Γ(u)∩Γ(v)|

(1)

其中，Γ(u)∩Γ(v)表示节点u与节点v所共有的邻居节点集合。

1.2 考虑共同邻居与节点度综合计算的指标

在CN指标的基础上，对CN指标所定义的相似性结合节点度等参数进行额外步骤计算，衍生出Salton指标、Jaccard指标等8种相似性指标。

(1)Salton指标[13]。

Salton指标在CN指标的基础上，计算过程融入了特定节点对的度参数，Salton指标也称作余弦相似性。

Salton指标如下：

(2)

其中，ku和kv为节点u、v的度。

(2)Jaccard指标[14]。

Jaccard指标在CN指标基础上，除以节点对u、v邻居并集的势。

Jaccard指标如下：

(3)

(3)Sorensen指标[15]。

Sorensen指标将CN指标的相似度值乘以2再除以节点对u、v的度之和。

Sorensen指标如下：

(4)

(4)HPI[16]与HDI[5]指标。

HPI(hub promoted index)大度节点有利指标主要用于新陈代谢网络研究，该指标认为节点对之间的相似度与二者度数中较小者成反比。HDI(hub depressed index)大度节点不利指标则认为节点对之间相似度与二者度数中较大者成反比。

HPI指标如下：

(5)

HDI指标如下：

(6)

(5)LHN-I指标[17]。

Leicht，Holme与Newman基于共同邻居思想提出了LHN-I指标，如下：

(7)

其中，节点u、v的度数乘积与相似度成反比。

1.3 考虑邻居度数的指标

在特定节点对的共同邻居中，拥有大节点度数的共同邻居，对特定节点对产生的影响、辐射往往会小于小节点度数的共同邻居。在该思想的基础上，先后出现了预测性能较好的AA指标和RA指标。

(1)AA指标[18]。

在AA指标中，根据共同邻居节点的度，为每个共同邻居节点赋予一个权重值，该值等于共同邻居节点度的对数分之一。然后将权重值累加，获得特定节点对之间的相似度。

(8)

(2)RA指标[19]。

周涛等受网络资源分配过程的启发，提出RA指标(resource allocation)。在RA指标中，权重值由AA指标中度的对数分之一的权重值变换为度数分之一。

(9)

RA指标与AA指标通过对共邻节点度进行权重差异化处理，主要体现在RA指标中为1/k递减，而在AA指标中为1/logk递减，因此当网络中的平均度很小时，AA与RA指标的计算结果近似一致。

1.4 考虑偏好连接的指标

在PA指标[20]中，在节点v和节点u之间产生无向边的概率，应该正比于节点u、v的度ku、kv之积。因此，在预测网络过程中，大度节点之间更加倾向于产生连接关系。PA指标在预测非常稀疏的路由网络中，效率与准确率都非常高。

suv=ku·kv

(10)

1.5 考虑自洽转移相似性的指标

孙舵等[21]在研究推荐系统时提出了转移相似性的概念，通过假设节点之间相似性可以传递来刻画节点之间的间接相似程度。该方法可以更加高效地利用已知的结构信息。以节点A与节点B相连，节点B和节点C相连的简单图为例，节点C、节点A分别与节点B之间建立相似性，B和C之间也建立了相似性，通过B的相似性传递，A与C之间也可能存在潜在的相似性联系。

TS指标如下：

(11)

其中，等号右侧第一项为间接相似性；等号右侧第二项suy为输入任意一种相似性指标得到的直接相似性；ε为可调参数，用以调节直接与间接相似性的比例。当直接相似性suy定义为邻接矩阵时，转移相似性矩阵可以等价表示如下：

STr=(I-εS)-1S

(12)

该方法由于需要原始相似性指标作为测度输入、涉及矩阵逆运算，算法客观上存在计算开销大的缺点。

2 一种基于转移偏好自洽相似性的链路预测方法

2.1 TSPA指标

上一节介绍了链路预测的常用相似性指标，在充分考虑节点度信息与网络结构信息的基础上，文中是将转移自洽相似性与偏好连接方法相整合，提出一种新的链路预测方法—基于转移偏好自洽相似性的链路预测方法(transferring similarity based on preferential attachment，TSPA)。

首先结合PA算法只考虑到了节点对的度数影响，且度数越高，二者连边概率越大。整合进TS方法，为把传递相似信息纳入，将PA方法与TS方法相结合，得到基于转移偏好自洽相似性的TSPA方法，定义如下：

(13)

通过变形，等价表示如下：

(14)

TSPA相似性理解可以从两个角度展开，一个是节点对之间已经存在的连边关系，另一个则是通过节点对的共同邻居的局部结构传递而具备的间接相似性。TSPA方法整合了PA与TS方法，在传统PA方法中只通过计算两个节点度数之积来建立相似性比较，而对间接的相似性信息没有充分加以利用。TSPA方法通过中间节点的传递特性，针对性克服了结构信息利用不充分的缺点。同时，TSPA方法中通过对ε参数的调优，可以看到中间节点相似性传递对特定节点对的影响大小，结合不同特性的网络，通过调节ε可以看到不同的预测结果。

2.2 TSPA算法设计

根据上一节描述，TSPA方法的算法描述如下：

输入：特定网络邻接矩阵M；

输出：相似性矩阵S，其中Su,v表示特定节点u、v产生连边关系的相似性得分，Su,v越大表示连边可能性越高，若Mu,v=1，则表示已经产生连边关系，在Su,v中直接置0。

算法步骤：

(1)构造列向量存储每个节点对应的度：

deg_row=sum(M,2)

将邻接矩阵M中每一行求和，即为每个节点对应的度的列向量。

(2)将列向量Deg乘以其转置，得到PA方法的相似性矩阵Sim：

Sim=deg_row * deg_row'

(3)结合PA测度输入，计算传递相似性矩阵：

S=(I-ε*Sim)-1*Sim

(4)删去S中值为1的已存在边元素：

S=S-S⊗M

在步骤4中，⊗表示两矩阵对应位置元素相乘,对应Matlab中的矩阵“.*”运算规则。

3 实验与分析

实验将现有的CN共同邻居算法、RA资源分配算法、PA偏好连接算法和提出的TSPA算法应用到复杂网络链路预测中的经典数据集，通过分析比较各算法对应的AUC值，对各算法预测性能进行对比分析。

3.1 实验数据集

实验采用7个复杂网络预测常用的数据集[2]，Router为Internet中路由器层次的网络，节点表示路由器，连边表示两路由器通过光纤等方式直连进行数据包交换；USAir为美国航空网络，每个节点对应一个机场，机场间若存在直达航线则表示存在连接关系；Yeast为蛋白质相互作用网络，节点为蛋白质大分子，若蛋白质之间存在相互作用关系则认为存在连接关系；PB为美国某政治论坛博客网络，博主为网络节点，如果博客间存在超链接关系则认为两个博主之间存在连接关系；NS为发表过复杂网络为主题的科学家合作网络，科学家为网络节点，如果科学家之间存在论文合作关系，则认为科学家之间存在连接关系；C.elegans为线虫的神经网络，节点由线虫的神经元表示，神经元的突触或者间隙连接存在，则认为神经元之间存在连接关系。

表1将7个复杂网络经典数据集以统计量的形式展现出来,其中N为网络节点数量，M为网络的边数，K为网络平均度，C为聚类系数，D为网络直径，L为平均最短路径。

表1 用于链路预测实验的网络基本统计特征

下面通过可视化的形式，展示测试的7个复杂网络中的路由器Router网络和PB博客关系网络的拓扑结构。具体如图1和图2所示。

图1 Router网络

图2 PB网络

3.2 评价指标

在链路预测算法评估中，存在AUC、精确度(precision)、排序分(ranking score)三个评价指标。精确度指标首先需要确定一个值L，L表示根据特定算法获得的前L个预测结果，然后在前L个结果中对比真实链路情况，找出准确预测的链路个数m，最终m/L的值即为精确度。精确度越大，则算法的准确度越高。排序分则考虑了测试集中边在最终排序总结果中的位置，取re为测试边在排序中的名次，集合H为未知边集合，则单条测试边排序分为RSe=re/|H|。遍历所有测试边进行累加求均值，即可得到最终的排序分，排序分越小，说明算法准确度越高。

AUC指标[22]在链路预测、机器学习等领域应用广泛。AUC指标从整体上把握衡量算法的精准程度，相比Precision指标[23]仅考虑前L条边的预测准确程度和Ranking Score指标[24]更多考虑所预测边的排序情况，AUC综合衡量算法的准确程度与实用性更强。

3.3 实验过程与结果

在实验过程中，将复杂网络经典数据集进行随机划分，训练集占总边数的90%，测试集占总边数的10%，每个数据集进行100次独立实验。在训练集计算过程中，通过先获取数据集节点对间的Sim相似度矩阵，然后通过相似度矩阵测算各类边的连边概率，得到AUC值，并结合独立实验次数，得到最终的AUC均值。

网络基本统计特征如表2所示。

表2 用于链路预测实验的网络基本统计特征

从不同种类算法的横向角度比较，TSPA指标在路由网络、航空网络、蛋白质网络、政治博客网络中取得了较好的预测结果。TSPA在和RA、CN这两个基于网络结构相似性预测性能较好的指标对比中，在路由网络这种低网络平均度、低网络聚类系数的环境下，取得了明显的预测优势。

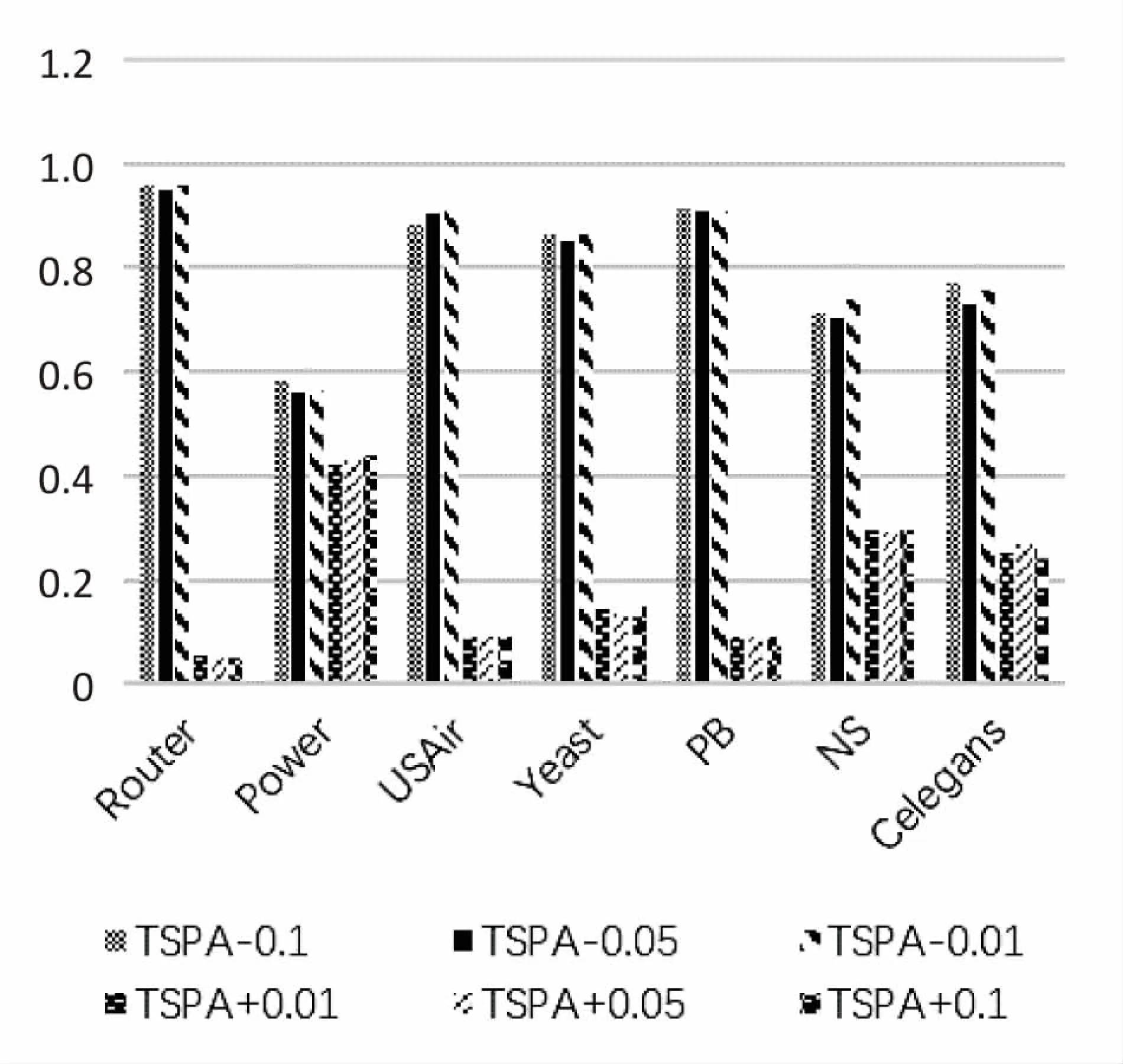
图3 TSPA取不同ε参数的AUC值

在TSPA指标与同源的PA指标类比中，在选取的三个ε参数(-0.1、-0.05、-0.01)中，分别在7个真实网络的预测中取得了对PA指标的5、1、6个网络的预测优势。即便在预测情况较低的参数(-0.05)下，剩余6个网络预测AUC值也和PA指标结果非常接近，体现了TSPA指标较传统PA指标的预测稳定性。具体如图3和图4所示。

图4 TSPA与其他方法的AUC值对比

通过将基于偏好连接方法获取的网络度结构信息，与转移自洽相似性方法相整合，形成的全新TSPA指标在真实网络预测中得到了有效验证。预测的AUC准确度结果在与一众经典链路预测指标对比中，建立了针对具体特征网络的预测优势，并通过ε值的对比分析，表明如果将ε值调整为正数，将对TSPA指标中最终预测结果产生反向降低AUC值的影响。

4 结束语

在综合利用节点度信息与网络结构相似性传递信息的基础上，提出了一种基于转移偏好自洽相似性的链路预测方法TSPA。该方法将节点对之间的度乘积信息形成的相似性矩阵，作为测度信息传入TS方法，并就具体的ε值进行验证。TSPA方法相比传统链路预测相似性方法，纳入了更多的网络结构信息，在对低平均度、低聚类系数的网络中展现出了更好的预测性能。

在后续的研究工作中，虽然TSPA在特定网络中的预测优势明显，但计算方法过程中涉及到矩阵求逆等操作，算法的时间开销相比CN、RA等方法存在一定劣势。在下一阶段工作中，一是在多样化研究和测试不同链路预测方法的基础上，对元路径的异质信息[25]、局部路径节点度幂指数规律[5]进行研究，降低对网络结构的计算规模，在提高或维持算法的预测精度的基础上，降低算法流程上的时间开销，使TSPA方法的预测效果得到进一步提高。