视觉遮挡下的手势协调神经网络模型
2019-08-22张少白诸明倩
张少白,诸明倩
(南京邮电大学 计算机学院,江苏 南京 210003)
0 引 言
随着科学技术的不断发展,机器的智能化程度也是日新月异。而机器人作为高新技术的代表[1],一直是近年来科学研究者所讨论的热点问题。它可以作业于一些相当恶劣的工作环境,从而大大降低人力资源的成本,保障工作人员的人身安全[2]。有关机器人的研究涉及到很多领域,比如计算机科学、传感器技术、生物科学等等[3]。而机械臂作为机器人的一个重要组成部分,已经成为机器人学领域一个重要的研究课题[4]。对此,许多相关领域的科研人员都做了相应的研究,并且取得了一定的成果。
Hoff和Arbib曾经构建了一种神经计算模型,该模型可以解决手臂移动以及手指预成型相关的各种问题。它是基于最小加加速度最优标准的计算模型[5],也是学术界公认的经典模型之一,但该模型是最早期的模型,因此不具有认知功能;Antonio Ulloa和Daniel Bullock在Hoff模型的基础上继续研究,提出了一种神经网络模型[6]。该模型是针对初始抓握角度、手掌的方向、被抓取物体的尺寸以及位置改变时手臂延伸和抓取间的时间协调问题的。该模型已经具备初步的认知功能,但并不系统;J. Molina Vilaplana和J. Lopez Coronado在2006年构建出抓握和移动过程中时空协调的神经网络模型[7]。该模型参考了DIRECT(direction-to-rotation effector control transform)模型和VITE模型(vector integration to end point),提供了手指间协调各种动作的方法,并且抓握过程中手势形成的策略也得到了简化;J. Molina Vilaplana和Rodolphe J Gentili于2011年在此前文章的基础上,提出了一种静态逆计算模型[8]。不仅具有文献[7]中模型所有的认知功能,而且将手臂延伸与抓握和灵长类脑区皮层神经元分布相关联。
但是Vilaplana的模型考虑的仅仅是一般情况下的手部抓取运动,并没有讨论在视觉遮挡时的情况。当视觉缺失时,该模型是否能继续适用,是否能进行准确抓握,这些问题都有待解决。因此,文中以Vilaplana的模型为基础,将手臂移动与手势抓取划分为四个阶段,即手臂收缩阶段、抓取物体阶段,手臂关节收缩阶段、物体释放阶段。讨论视觉对各个阶段的影响程度,在此基础上对Vilaplana的模型进行改进,使之能够适应视觉遮挡下的抓取运动。
1 手势协调的神经网络模型
1.1 计算模型
Vilaplana提出的模型如图1所示,该模型为分布式运动神经结构提供了对象的位置,大小,形状和方向信息。图1的左半部分描述了实现该运动的传输组件计算模型。物体位置的视觉信息为神经控制器提供相应的数据,为正确的抓取提供合适的位置信息。图1右半部分中所示的运动结构,保证了合适的手指预成型以及正确的手掌方向。需要注意的是,抓取有关的视觉通道被分成两个子通道,一个与手指结构相关,另一个与手掌方向相关。手掌方向的模式使用对象的外在属性,如方向来确定。模型中包含了另一种必须被送到抓取通道的信息。这种信息是与任务要求相关的[9]。显然,不管对象的外在方向是什么,与抓取相关的运动程序都必须考虑需要完成的任务。例如,不同的抓取意图会导致不同的手掌方向和抓取的最终手势,就比如想要准确抓取圆柱表面和插入圆柱上的一个孔会导致不同的抓握方式。

图1 手势协调神经网络模型
图1右下角的VITE模型[10]实现手指预成型和手掌方向的确定,左下角的DIRECT模型[11]实现传输组件的运作。与手势和手掌方向相关的运动方案也要考虑意图或者任务限制,如抓取的种类(抓取精度或力度)。一个共同的GO信号作为门控机制来调节启动过程和动作的执行速度,保证所有通道的时间等效。
1.2 手指预成型和手掌朝向
端点间的矢量积分(VITE)动力学被用于模拟抓取过程中的手指预成型神经通道[12]。在该通道中,手势用一个二自由度的系统来模拟,这个系统与系统效应(w1,w2)的时间比重有关。其中w1和w2是用于产生各种手势的两个协同时间比重,产生方式如下所示:
θ=S1w+S2
(1)
其中,θ表示仿人运动手模型具有15个自由度的向量;S1是一个15*2的矩阵,这个矩阵含有一个作为列向量的两协同作用的数字模型;S2是一个偏置向量,具体的原理已经由Santello说明过[13]。
1.3 DIRECT模型
负责手臂移动的DIRECT模型是一种自组织神经网络模型,该模型解释了作为人类达到行为特点的灵活性和强大性的许多方面。模型的中心是对目标导向控制的视觉、空间以及运动表示的形成方式进行分析。
DIRECT模型主要实现从空间方向到关节旋转的坐标变换。模型主要包括两个部分,一是处理阶段的流程,该阶段允许外部目标位置在到达任务时引导末端执行器位置的变化。首先,必须计算目标的空间坐标。在DIRECT模型中,目标位置的三维体心表示通过神经网络来计算,该神经网络由视觉,眼部位置以及头部位置信息组成。利用视网膜,眼运动,颈部运动信号来完成变换的神经网络曾由Greve等[14]说明过。然后,空间差分向量(DV)通过比较目标位置表示与末端执行器位置的表示来计算,在相同体心坐标系中测量。空间差分向量编码了方向和大小信息。它指定了所需的空间位移,使端部执行器与目标接触。第三,空间到运动转换计算了关节角度的变化,或旋转,该旋转使末端执行器沿着空间差分向量移动到目标位置。因为这个转换计算了产生所需空间运动方向的关节旋转,也可以被称为direction-to-rotation转换。计算合适的关节角度变化需要空间DV的方向和现在关节配置的信息。因此direction-to-rotation阶段的来自编码关节角度阶段的另一个输入也被进行了描述。最后,在前馈流程的第四个主要阶段通过direction-to-rotation信号完成角度递增或者递减的整合。该阶段的输出指定所有关节的角度设置,从而控制末端执行器的位置。为了确保指定的关节角度变化和实际执行器位置变化之间的紧密联系,需要一个方案来解决逆动力学问题。该讨论存在一个假设,就是该问题可以通过额外的神经回路来解决,如由Bullock and Grossberg在FLETE[15]模型中分析过的脊髓和小脑电路。
第二部分是三个不同的反馈回路。第一个回路用关节角度积分来更新direction-to-rotation转换。关节角度积分也用来更新多模式阶段,该阶段可以使用关节配置输入或视觉上的输入来计算端部执行器的空间坐标。这需要一个中间运动-空间转换来将关节配置信息转化成用于轨迹形成的空间坐标系。末端执行器位置的空间表示是相对于用来计算空间DV的目标位置空间表示的,从而关闭第二反馈回路。本体感觉信息也可以在这些性能中使用,形成额外的反馈回路(图中未示出),从而增加刚刚讨论的两个回路。第三个也是最长的反馈回路,是存在于可见末端执行器时的一个外部循环。它的空间坐标能够通过将其视网膜图像转化为一个三维体心空间表示来计算。它被用于多模式阶段,在多模式阶段可以将关节配置输入相结合来估计末端执行器位置。
总之,在运动周期中,目标位置和末端执行器的位置之间的任何差异都会在空间DV阶段被记录,空间DV阶段的输出转换成相应的关节旋转。随着关节旋转,内部反馈确保direction-to-rotation转换将会被调整以反映新的关节配置。随着运动的进行,无论是到多模态阶段的内部或外部反馈都将更新末端执行器位置的内部表示。因为这种在目标方向上,空间DV上变化的表示被逼近于零。当末端执行器位置和目标位置的内部空间表示相一致以及空间DV等于零时,该移动将自我终止。
如上所述,内部和外部反馈回路是为了更新末端执行器位置的内部表示而存在的。内部循环更快,而且可以用来避免滞后的不稳定性。因此,通过内部反馈循环更新在快速移动或者较慢运动高速度段时是最好的。但是为了准确度,较慢的视觉反馈是可取的。这些考虑可以提供两方面的优化性能。首先,当移动速率低时,可以使视觉反馈占主导地位,当移动速率高时,内部反馈占主导地位。其次,它可以在运动过程中进行速度分配,从而允许为了进行准确视觉引导的终端低速阶段。
2 视觉遮挡对抓握孔径的影响
抓握动作是日常生活中的一种典型动作。Jeannerod提出,抓握动作由两个主要部分组成:传输组件和控制(抓握)组件。在抓握组件系统中,首先手指会逐渐打开,之后会根据被抓握的物体尺寸形成合适的结构,然后继续张大以达到一个比目标物体尺寸更大的最大值,也就是峰值抓握孔径,然后开始闭合直至接触到物体表面。已经有研究表明,在抓握过程中视觉缺失时,峰值抓握孔径(PGA)会明显增大[16],因此PGA被认为是抓握过程中在线视觉影响的表征。虽然不清楚为什么抓握孔径会发生超调现象,或者说为什么缺少在线视觉时,PGA会变得更大,一种可能的原因就是抓握孔径的变化可以允许运动过程中的误差以及防止手指与目标物体之间的碰撞[17]。
为了更直观地了解视觉的影响,可以进行下面这样一个实验。实验者配备有液晶快门护目镜并以一种舒适的姿势坐在桌子前面,如图2所示。目标物体(c)摆放在距离实验者50 cm的地方,开始位置(a)与实验者右肩在一条直线上,并放有一个压力感觉开关。用两个圆柱体(直径为4 cm或者6 cm,高为11 cm)作为目标物体。电磁运动跟踪传感器用于检测拇指,食指以及手腕的位置,两个直径1 cm的球形微型接收器连接到拇指和食指的指尖,一个立方体的接收器(b)(宽2.8 cm,长度2.3 cm,高1.5 cm)附在手腕上。每个接收器的时间分辨率为120点/秒(每个接收器连接到每个系统的电子单元),空间分辨率为0.8 mm。液晶快门眼镜大约3 ms变透明,约20 ms变成不透明。实验者需要将圆柱体从c移动到d处。
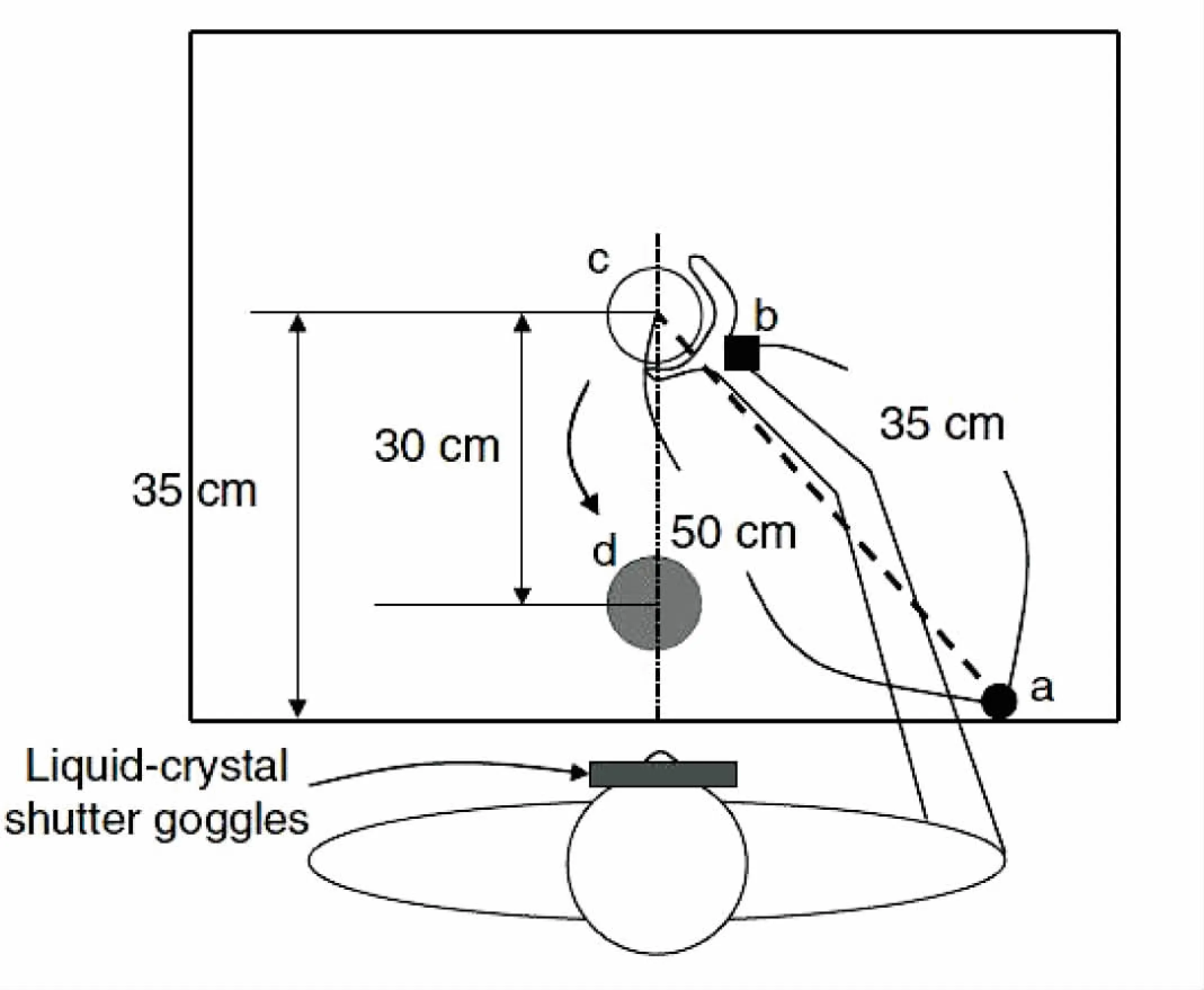
图2 视觉遮挡实验装置
实验前,参与者将右手放在起始位置,食指与拇指相互接触,此时的眼镜是不透明的。当接受到一个go信号时,眼镜变得透明,之后实验者就开始移动手臂。整个运动过程持续的时间为1 100 ms。接着根据实验者视觉被遮挡的时间划分为六种情况:完全没有视觉(NV);从150 ms的时候开始关闭眼镜(150S);从350 ms的时候关闭眼镜(350S);从500 ms的时候开始关闭眼镜(500S);从700 ms的时候开始关闭眼镜(700S);整个过程眼镜都是透明的(FV)。每个实验者都需要进行32次练习实验以熟悉任务并确认所要执行任务的细节。实验数据如图3所示。

图3 六种情况下的各个运动学参数
从图3的数据可以看出,遮挡的时间越长,最大抓握孔径就会越大。由此可以得出,视觉遮挡将会导致抓握孔径变大,因此在构建的模型中需要增大手指预成型时的最大抓握孔径以补偿视觉的不确定性,从而实现视觉遮挡下的抓握。
3 新模型的构建
3.1 视觉遮挡下的最大孔径计算模型
根据主成分分析法,Schlicht和Schrater认为[18],当目标物体放在不同的可见位置时,只有一个主要因素可以解释伸手抓握过程中手指运动轨迹的差异,这个因素可以通过手的孔径大小来表示。因此,应该对拇指和食指之间的抓握孔径而不是每个手指的运动进行建模。控制抓握孔径的动作指令在有延迟和干扰的情况下被传送到末端执行器(手),然后抓握孔径发生变化。
同时,运动命令被复制并发送到状态估计器,这个过程毫无延迟,同时身体运动状态(抓握孔径)也会被模型所估计。所估算的抓握孔径与感觉反馈进行比较,而感觉反馈来源于视觉和抓握孔径实际感受。估计误差被用来纠正对身体状态的估计。然后根据预测的身体状态和估计的不确定性来生成运动指令。视觉所观察到的目标物体的大小及其不确定性也被用来生成运动指令。
3.2 视觉遮挡下手势抓握模型的构建
为了应对视觉不确定性对手势抓握的影响,可以将上述模型应用于Vilaplana的模型中,构建出新的模型,在视觉被遮挡的情况下适当增大峰值抓握孔径以避免手与目标物体之间的碰撞,从而顺利完成抓握。新的模型如图4所示。

图4 视觉遮挡下的手势抓握模型
4 抓握孔径的计算
4.1 抓握孔径模型
为了对抓握孔径进行计算,首先需要对抓握过程建模,模型如图5所示。手沿y轴从起始位置移动到目标位置,手指孔径沿着x轴打开,考虑到手和目标物体的不确定性,为了避免伸手抓握过程中不希望出现的碰撞,抓握孔径必须有安全冗余。物体在x轴的位置和物体直径分别记为x0、s0,物体右边边缘位置是x0+s0/2。手的位置和抓握孔径大小分别被记为xh和a,物体右边手指的位置是xh+a/2。为了避免手指与物体发生碰撞,手指必须在物体边缘的右边,即x0+s0/2 图5 抓握孔径模型 (2) 这是一个累积分布函数,用来描述在有高斯噪声的情况下,抓握孔径a大于目标物体s0的概率。 为了在不确定情况下完成抓握动作,CNS必须考虑发生碰撞的风险。如果考虑一个特殊概率Ф,CNS令其为成功率,所要获得的抓握孔径就可以由这个公式计算得出:a*=Ф-1(Ф,s0,σ)。 注意,Ф是CNS在完成动作前在有不确定性和变化的情况下(即σ2)预测的概率,这个不确定性和变化也是由CNS估算出来的。这个Ф并不代表抓握动作真实的成功率。这里,孔径a*为目标孔径。一旦目标孔径确定,控制器就生成动作指令来移动抓握孔径靠近目标孔径。 抓握动作可以由一个状态空间表达式进行建模: xt+Δt=Fxt+Dut+Gwt (3) (4) (5) (6) (7) 控制器此时确定的不是整个轨迹,而是t时刻的瞬间加速度。基于等式5,t+Δt时刻抓握速度是: (8) ut=b1+b2Δt (9) 虽然动作指令是由现有孔径和目标孔径计算得出,但是CNS并不知道此时身体动作的真实状态。身体动作的状态信息必须通过感官系统获得。在这里,抓握孔径是通过视觉和本体感受得出的。 yt=Hxt+vt (10) (11) (12) (13) 这些等式基于估算的身体状态产生动作指令。 现实中的大脑-身体系统在动作指令上有传输延迟和感官反馈回路。当动作延迟和感官延迟分别用dm和ds表示时,式3和式10可以被修改为: xt+Δt=Fxt+Dut-dm+Gwt (14) t时刻产生的动作指令必须基于t+dm时刻的身体状态(估算值),这里式12和式13被修改为: (15) (16) 这个等式表明此刻大脑意识到的身体状态提前于真实的身体状态。这个函数对可预测重映射十分重要,其中有计划地扫视运动的神经表达式被加以修改去弥补眼睛位置未来的变化。同样的,在伸手抓握过程中,抓握孔径也必须在动作指令到达执行器之前被预测到。 实验将对新模型进行仿真,并将实验结果与Vilaplana模型中得出的结果进行比较。Vilaplana模型是在视觉可见的情况下进行的仿真,将两者进行对比可以得出新模型的各项性能。仿真实验中,分别将目标大小设置成6 cm直径的圆柱体,通过几组实验对比,观察手臂的移动速度、抓握孔径以及总的移动时间的变化情况。实验情况如图6所示: (a)抓握孔径变化情况 (b)抓握速度变化情况 图6(a)中数据记录的是在视觉遮挡后抓握孔径的变化情况。可知在对视觉进行遮挡后,模型的最大抓握孔径变大了,这样就有了一定的安全冗余,避免了手与物体之间的碰撞,模型通过增大抓握孔径补偿了感官上的不确定性。 图6(b)是为了验证该模型的改进对手臂移动过程的影响,记录改进前后的手腕速度。从图中可以看出,当模型改进之后,手腕速度的变化并不是很大,只是有轻微的振荡。由此可见,视觉遮挡下的手臂移动也能够正常进行。 通过对Vilaplana模型进行深入研究,考虑到视觉遮挡这一特殊情况,对手指预成型部分进行改进,构建出视觉遮挡下的手势抓握模型。实验结果证明,模型的改进并不会对手臂移动过程产生较大影响,而且通过增大抓握孔径来补偿视觉的不确定性,使其能够在缺少视觉反馈的情况下完成手臂移动以及抓握动作,大大扩展了模型的应用范围。 但是,该模型仍然存在许多问题,需要进一步完善,对于心理学和认知学方面的东西涉及不多,模型的智能化程度还需要一定提高。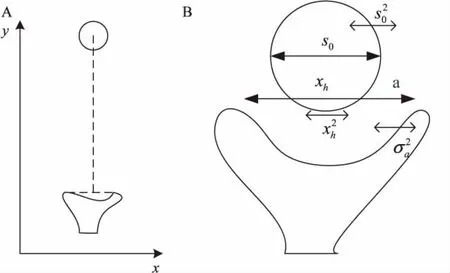


4.2 孔径尺寸计算

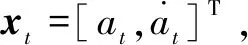



5 实验仿真


6 结束语
