金属光子晶体的可见光光谱特性

赵亚丽，马富花，贾 琨，李旭峰，王 权，雷忆三，张 捷

(1.晋中学院，山西 太原 030619;2.电磁防护材料及技术山西省重点实验室，山西 太原 030006;3.太原科技大学 应用科学学院，山西 太原 030024)

1 引言

随着电子设备集成度和精密度不断提升，要求光学窗既要保持良好的可见光透光率从而不影响图文和图像的观察效果，又具备较强的电磁抗干扰能力，以保证电子设备正常工作。目前，抗干扰能力强的材料多为金属。而在金属中存在大量的自由电子，它们对电磁场的响应使得金属从可见光到近红外频段都表现为有损和强色散的特性，尤其是其真空磁导率和实部小于零的负介电常数，导致金属不支持可见光传输。这使得电磁屏蔽和透光率在一定程度上是相互制约的。目前还没有一种单一材料兼具良好的可见光透光率和电磁屏蔽效能。我们在研究中发现，与ITO(In2O3∶Sn锡掺氧化铟)和AZO(ZnO∶Al铝掺氧化锌)透明导电薄膜相比，金属光子晶体(Metal photonic crystals,MPCs)具备较强的电磁屏蔽性能[1-2]。MPCs这一特性使其在电子设备光学窗领域具有广阔的应用前景。

MPCs是由金属薄膜和电介质薄膜周期排布构成的。当可见光入射到MPCs时，会在金属和介质的界面产生表面等离子激元(Surface plasmon polariton，SPP)[3-6]。当金属膜层较薄时，分布在不同界面的SPP会产生多重耦合。在这种SPP耦合的作用下，原本在金属中不能传输的可见光能够很好地穿透MPCs。金属膜层越薄，其SPP耦合越强，可见光透光率曲线越宽，透光率越高。而当金属膜层的厚度一旦大于4倍的SPP的穿透深度时，SPP耦合效应会急剧降低，其界面的SPP耦合效应几乎不发生，可见光透光率也相应降低[7-9]。这样，在单一金属中被抑制传播的可见光，能够在MPCs中很好地传播。为此，这种透光的MPCs又被称为透明金属[7-9]。

与AZO/Ag/AZO[10]、ZnO/Ag/ZnO[11]、AZO/Au/AZO[12]、ZnO/Cu/ZnO[13]等金属多层透明薄膜相比，MPCs可见光透光率曲线的中心波长和频谱宽度具有可设计性[1,14]。研究表明，金属组分比越低，MPCs可见光透光率中心波长越长，频宽越宽[14-15]。同时，也开展了周期等参数对其MPCs禁带特性的研究。研究表明，在金属组分一定时，MPCs周期大到一定程度时，会在可见光范围产生禁带，抑制可见光在MPCs中传播[16-17]。然而，除了金属和介质膜层的组分比，其周期大小和周期数也会对可见光透光率产生影响，而目前关于这方面的研究较少。本文采用时域有限元差分法(FDTD)研究了MPCs的周期、周期数和入射角度等对MPCs的光谱特性的影响。这些研究对基于MPCs的光学窗色感和色彩饱和度的设计具有重要的意义。

2 研究模型和方法

2.1 研究模型

本文设计的MPCs是由金属Ag和电介质ITO膜呈周期排布构成的。与包含Cu和Al的MPCs相比，含Ag的MPCs具备更高的可见光透光率[18]。而Au膜在可见光波段损耗高，将会有很大一部分能量被损耗掉，难以激发产生SPP。相比之下，Ag膜在可见光损耗较低，能够有效激发SPP。因此，本文将Ag作为MPCs的金属组分。另一方面，由于ITO薄膜兼具良好的透光率和导电性，因此选取ITO薄膜作为MPCs的电介质膜层[19-20]。本文设计的MPCs的结构见图1。

图1 MPCs的结构示意图Fig.1 Sketch map of designed MPCs

根据以往的研究，发现当金属Ag和ITO膜厚比为1∶4时，其可见光透光率中心波长为500 nm[2]，且当周期数大于3.5后，MPCs的电磁屏蔽效能不再随周期数的增加而提高[1]。为此，在本文中金属Ag和ITO膜厚比设计为1∶4。除了研究周期数对MPCs光谱性能的影响外，MPCs的周期数设定为3.5。另外，由于SPP模场在金属Ag膜的穿透深度为22 nm[7],而金属在小于10 nm时，金属Ag未形成连续薄膜，由此，将金属膜层设计为10～30 nm。

2.2 研究方法

采用时域有限差分法(Finite difference time domain，FDTD)对MPCs的可见光光谱性能进行计算仿真。根据算法的收敛准则，在x-y平面内将单元网格划分为1 nm×1 nm(该尺度远小于入射波长的1/10)，以确保计算结果的准确可靠。对计算边界的处理：在x方向选用布洛赫(Bloch)边界条件，y方向选用PML吸收层用于吸收向外散射的电磁波[21-22]。在波长200～1 000 nm的范围内，金属的介电常数采用Lorentz-Drude方程获得，如公式(1)所示[23-24]：

ε=ε′+iε″=ε

(1)

其中ε、ε′和ε″分别为Ag薄膜的介电常数、介电常数实部和虚部，而ε为金属带间跃迁对介电常数的贡献。在远离带间跃迁频率时，ε为常数，其中金属Ag的ε=5。金属Ag薄膜的等离子频率ωp=14.0×1015rad/s，而阻尼系数Γ=0.032×1015rad/s[24]。采用椭偏仪对制备的100 nm厚ITO薄膜的介电常数进行测量，其大小为3.13。

3 结果与讨论

3.1 MPCs周期对其光学性能的影响

MPCs周期数和金属介质膜厚比分别固定为3.5和1∶4，采用FDTD对不同周期的MPCs的可见光透光率和反射率进行计算仿真。根据MPCs的等效介质理论，当金属和电介质膜厚比一定时，MPCs的等效介电常数是相同的[2]。为此，通过本部分研究，获得了在等效介电常数不变的条件下，MPCs的周期对其光学性能的影响。不同周期的MPCs的结构见表1。

不同周期MPCs可见光透光率如图2所示。当MPCs中Ag和ITO膜厚分别为10 nm和40 nm常数时，由于两者厚度都小于SPP穿透深度，产生的SPP耦合效应不明显，可见光透光曲线与单层金属薄膜的相似。由于金属Ag的等离子波长在400 nm附近，样品S1在400 nm处可见光透光率最高。S1第二个可见光透射峰源于MPCs的SPP耦合效应，耦合较弱，峰值不明显。通过比较图2(a)、(b)、(c)、(d)图，可得：

表1 当ITO膜为最外(内)层时，不同周期的MPCs的结构Tab.1 MPCs parameters of samples with different period size when ITO film is the outermost(innermost)layer

图2 采用FDTD计算不同周期的MPCs的可见光透光率。(a)样品S1；(b)样品S2；(c)样品S3；(d)样品S4。Fig.2 Optical transmittance of MPCs with different period.(a)Sample S1.(b)Sample S2.(c)Sample S3.(d)Sample S4.

(1)当每层ITO膜厚大于60 nm时，透光率曲线会产生两个透射峰，且随着ITO膜厚的增加，两个透射峰间距在不断减小。

(2)当ITO膜厚大于60 nm时，MPCs最大可见光透光率随周期的增加而相应降低。当膜厚为75，100，150 nm时，MPCs的最大透光率依次为90%、85%和70%。

(3)当每层ITO膜和Ag膜分别为120 nm和30 nm时，透光率中心波长明显红移。另外，随周期的增加其可见光透光率的截止波长是不变的，S1、S2、S3和S4的截止波长都约为700 nm。

值得注意的是，当MPCs中ITO和Ag膜分别为120 nm和30 nm时，500 nm处的可见光透光率曲线消失，透光率的峰值发生红移，分析其主要原因是大的结构周期导致MPCs在可见光范围出现结构能带而抑制可见光传输。其中，MPCs结构禁带中心波长由公式(2)给出[25]：

λ=2na，

(2)

其中λ为结构禁带的中心波长，而a为一维MPCs的周期，其大小见公式(3)：

a=d1+d2，

(3)

其中d1和d2分别代表每个周期ITO和Ag膜厚。

n为MPCs等效折射率，其大小为[26-27]：

(4)

当MPCs中单层膜厚远小于可见光波长时，MPCs的介电常数满足等效介质理论，即[26-27,23]

(5)

其中ITO和Ag薄膜的介电常数分别对应εd和εm。η为单位周期中金属Ag膜厚(d2)和ITO膜厚(d1)的比值:

(6)

根据公式(5)可得：MPCs金属和介质膜层组分比不变时，其εeff就为定值。根据公式(2)，在n一定的条件下，其结构禁带的中心波长直接取决于周期a，a越大其禁带的中心波长就越大。为此，当MPCs周期为150 nm时，在500 nm附近出现了可见光结构禁带，抑制了可见光的传输。而可见光传输的截止波长是由于其对应的等效介电εeff<0造成的。根据公式(5)，在金属Ag和ITO膜厚比一定时，对应的截止波长是一样的。因此，S1、S2、S3和S4样品的截止波长都为700 nm。

图3 采用FDTD计算不同周期的MPCs的可见光反射率，(a)、(b)、(c)和(d)对应表1中S1、S2、S3和S4样品。Fig.3 Optical reflectance of MPCs with different periods by FDTD.(a),(b),(c)and (d)corresponding to the samples of S1,S2,S3 and S4.

为了进一步研究MPCs周期对其光学性能的影响，对S1、S2、S3和S4样品的可见光反射率也进行了计算仿真，MPCs的反射谷和透射峰对应的波长具有较高的一致性。由此可见，MPCs的高透光是由于其低反射引起的。

同时对以Ag膜为最内层和最外层样品的光学性能也开展了研究，见表2。将Ag薄膜作为最内层和最外层时，MPCs存在附着力差和易氧化等不足。本文为研究在其他参数一定的条件下，表1和表2两种不同结构的MPCs的光学性能，特对Ag膜为最外层和最内层的MPCs(见表2)的可见光透光率和反射率进行研究。

和S1、S2、S3和S4相比，S5、S6、S7和S8的可见光透光率具有相似的规律(如图4)，一方面，可见光透光率随周期增加而相应降低；另一方面，可见光透射峰也随周期的增加而相应增多。除此之外，S5、S6、S7和S8样品的可见光透光率也表现出以下几点不同：

表2 当Ag膜为最外(内)层时，不同周期的MPCs的结构Tab.2 MPCs parameters of samples with different period size when Ag film is the outermost(innermost)layer

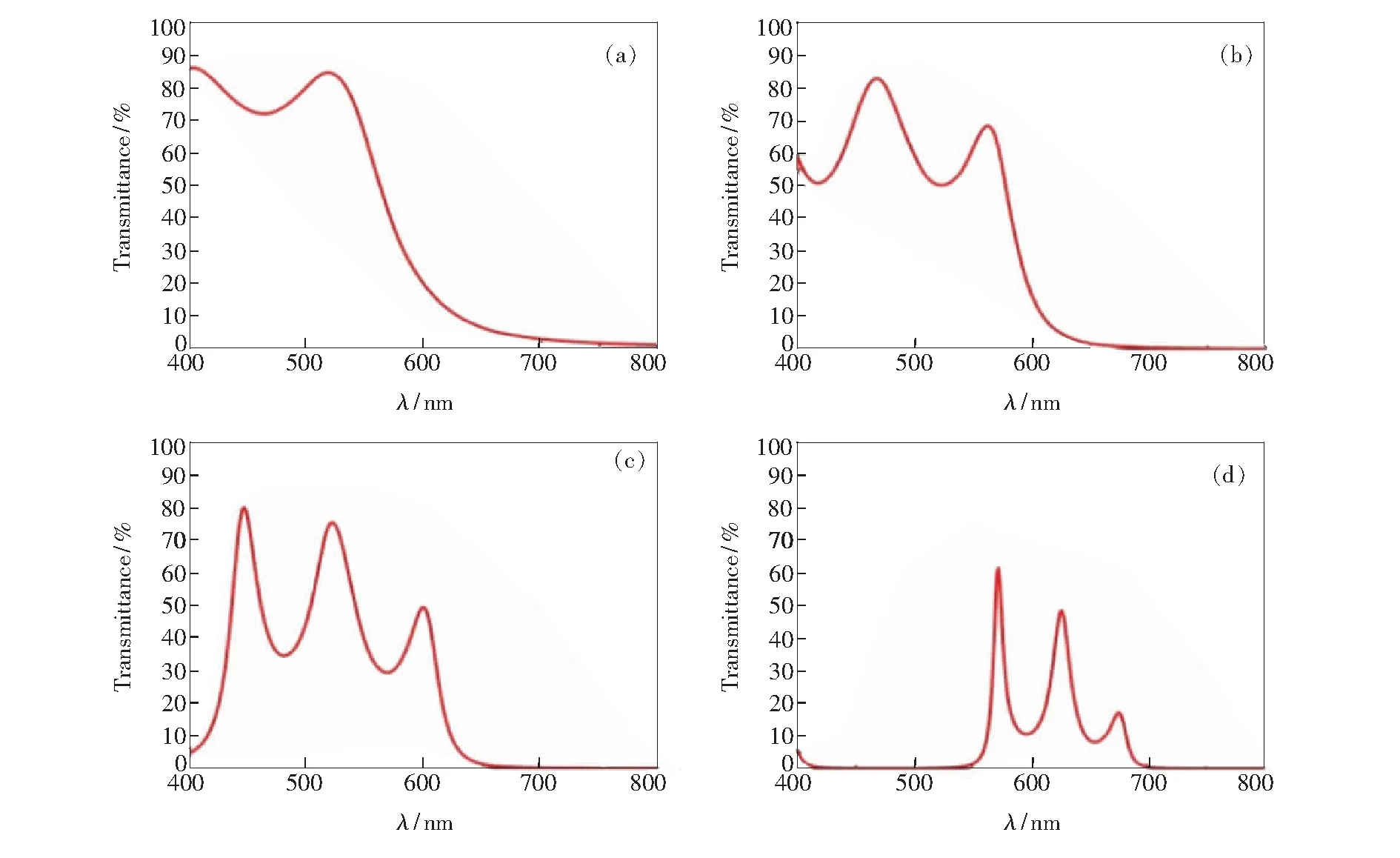
图4 采用FDTD计算不同周期的MPCs可见光反射率，(a)、(b)、(c)和(d)对应表2中S5、S6、S7和S8样品。
Fig.4 Optical reflectance of MPCs in different periods by FDTD.(a),(b),(c)and (d)corresponding to S5,S6,S7 and S8 samples.

(1)对应每个周期，可见光透光率曲线都相应增加1个透射峰。由于当金属Ag膜处于最内层和最外层时，会在玻璃与金属、空气与金属界面处形成表面等离子激元。而当金属薄膜与不同介质接触时，产生的表面等离子激元波矢也不同，如公式(7)[28]：

(7)

其中ε1为金属相临的介质的介电常数，在本文中代表空气、玻璃和ITO膜层的介电常数。因此，将金属Ag膜作为最外层和最内层，激发的SPP及耦合模式也会相应增加，可见光透光率曲线的透射峰也相应增加。

(2)在MPCs周期小于100 nm时，S5、S6、S7和S8样品的可见光透光率曲线会变宽。这主要是由于金属Ag作为最内层和最外层时，产生了较多的SPP模式，这在一定程度上会拓宽MPCs的可见光透光率曲线。而当MPCs膜厚大于100 nm时，由于大周期产生结构禁带抑制了MPCs透射曲线变宽。

(3)当最内层和最外层采用金属膜时，对应不同周期的MPCs的可见光透光率都相应下降。当周期为75 nm时，最大可见光透光率从90%下降到85%。这是由于损耗较大金属Ag膜层层数增加，使MPCs可见光透光率相应降低。为此，相比于S1、S2、S3和S4，S5、S6、S7和S8的可见光透光率都明显降低。

由此可见，将金属Ag膜作为最内层和最外层时，可见光透光率曲线的透射峰相应增多，曲线相应变宽，最大可见光透光率相应降低。

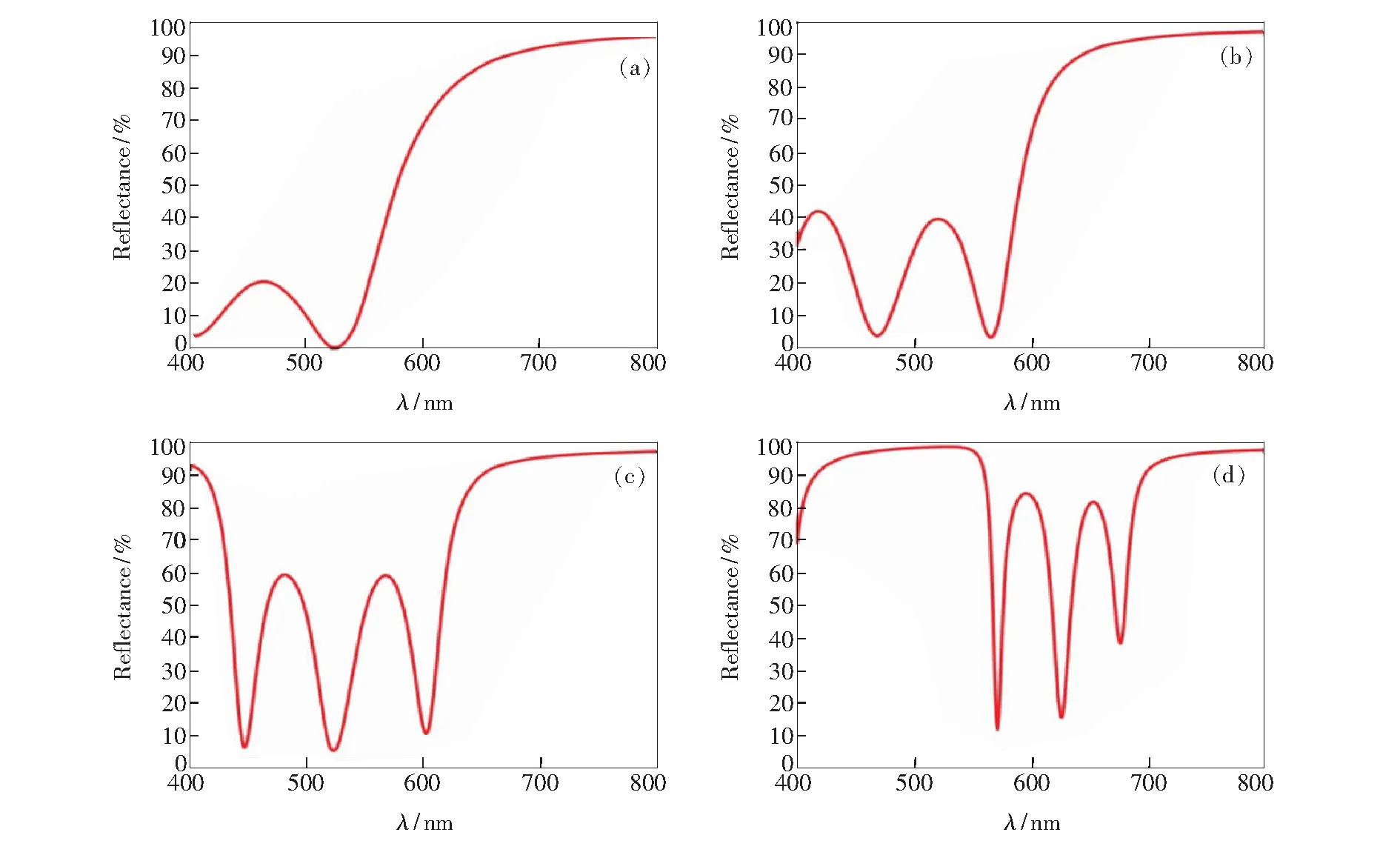
图5 采用FDTD计算不同结构的MPCs的可见光反射率，(a)、(b)、(c)和(d)对应S5，S6，S7和S8样品。Fig.5 Optical reflectance of MPCs with different structures calculated by FDTD.(a),(b),(c)and (d)corresponding to S5,S6,S7 and S8 samples.

同样，采用FDTD对S5、S6、S7和S8的可见光反射率也进行了计算仿真，如图5所示。研究结果表明其可见光透光率峰值和反射率的峰谷具有较高的一致性。该结果再次说明，MPCs对可见光的高透过源于MPCs的低反射。

3.2 MPCs周期数对其光学性能的影响

为研究MPCs周期数对其可见光透光率的影响，本文分别对周期为Ag(15 nm)/ITO(60 nm)和Ag(20 nm)/ITO(80 nm)、周期数为2.5～7.5的样品的可见光透光率进行仿真计算，分别如图6和图7所示。

从图6可以看出，当MPCs的周期数为2.5时，其可见光透光率变化趋势与单层金属薄膜相类似。随着周期数增加，可见光透光率共振峰相应增加，可见光透光率曲线半高宽变宽。这是由于随着周期数增加，金属Ag膜层层数也相应增加，形成金属Ag和ITO薄膜的界面数也相应增加，Ag的SPP共振模式及耦合模式也相应增多，因而可见光透光率曲线相应变宽。一方面，MPCs薄膜可见光透光率由于SPP耦合强度增强而提升；另一方面，由于金属反射，可见光透光率也会降低。如果SPP耦合增强发挥作用大，随周期数增加，MPCs可见光透光率不降低，甚至升高[1,29]。反之，MPCs可见光透光率急剧下降。基于以上两种物理过程的相互竞争，MPCs可见光透光率随着周期数的增加而缓慢降低。而当MPCs周期数为7.5时，尽管MPCs总金属膜厚(105 nm)远大于可见光在金属中的趋肤深度，MPCs依然表现出良好的可见光透光率。

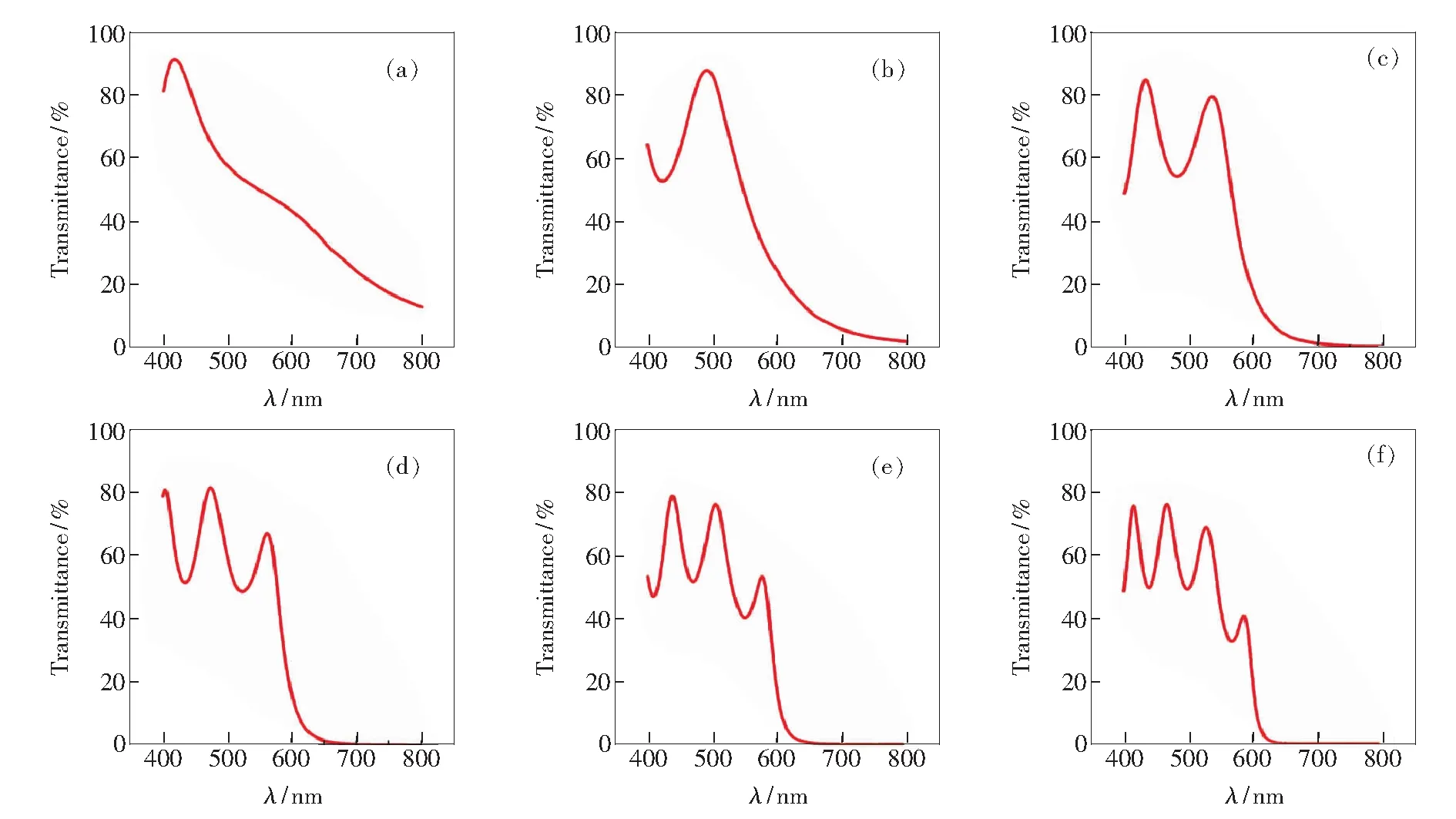
图6 FDTD仿真计算[ITO(60 nm)Ag(15 nm)]n/ITO(60 nm)型MPCs可见光透光率曲线。(a)n=2.5；(b)n=3.5；(c)n=4.5；(d)n=5.5；(e)n=6.5；(f)n=7.5。
Fig.6 Optical transmittance of [ITO(60 nm)Ag(15 nm)]n/ITO(60 nm)MPCs，which is obtained by mean of FDTD.(a)n=2.5.(b)n=3.5.(c)n=4.5.(d)n=5.5.(e)n=6.5.(f)n=7.5.

图7 FDTD仿真计算[ITO(80 nm)Ag(20 nm)]n/ITO(80 nm)型MPCs可见光透光率曲线。(a)n=2.5；(b)n=3.5；(c)n=4.5；(d)n=5.5；(e)n=6.5；(f)n=7.5。Fig.7 Optical transmittance of [ITO(80 nm)Ag (20 nm)] n/ITO(80 nm)MPCs，which is obtained by mean of FDTD.(a)n=2.5.(b)n=3.5.(c)n=4.5.(d)n=5.5.(e)n=6.5.(f)n=7.5.

与含15 nm的Ag薄膜的样品相比，含20 nm的MPCs可见光透光率随周期增加，透射峰相应增加，而透射强度相应降低。但含20 nm的金属的MPCs的可见光透光率强度下降较快。当周期从2.5增加到7.5时，含15 nm的金属膜的MPCs，从90%下降到78%；含20 nm的金属膜的MPCs，从90%下降到70%，如图6和图7所示。这主要是由于含20 nm的Ag膜的MPCs的SPP耦合较低，界面反射较强。

3.3 入射角度对其MPCs光学性能的影响

采用FDTD对表3中的S9、S10和S11样品在不同入射角情况下的光学性能进行仿真计算，以研究其入射角度对可见光透光率曲线的影响，见图8。

表3 不同结构的MPCsTab.3 MPCs parameters of samples with different pairs in third group

图8 采用FDTD计算不同入射角MPCs可见光反射率。(a)和(b)、(c)和(d)、(e)和(f)分别对应表3中S9、S10 和 S11样品。Fig.8 Optical reflectance of MPCs at different incident angles obtained by means of FDTD.(a)and (b),(c)and (d),(e)and (f)correspond to S9，S10 and S11，respectively.

研究表明，随着入射角的增加，MPCs透光率中心波长发生蓝移，可见光透光率强度相应降低。特别是当入射角从60°提高到75°时，可见光透光率急剧降低。而当其入射角继续增大到90°时，在较宽的波长范围内薄膜可见光透光率低至10%以下。比较图8(a)、(c)、(e)图和(b)、(d)、(f)图，发现其金属膜层越厚，随着入射角度的增加，MPCs可见光透光率(反射率)降低(提高)得越快。

4 结论

本文通过对MPCs周期、周期数及入射角度对其光学性能的研究，得到如下结论：

(1)相较周期含40，80，120 nm的ITO薄膜，含60 nm的ITO膜的MPCs更易形成SPP耦合，获得较高的可见光透光率。随ITO膜厚增加，MPCs透光率曲线会出现多个透射峰。将金属膜层作为MPCs最内层和最表层时，由于在金属与衬底、金属和空气层界面会激发SPP新模式，MPCs可见光透光率曲线峰值数会相应增加，透光率曲线也相应展宽，MPCs可见光透射峰和反射谷的对应波长具备较好的一一对应关系。

(2)随周期数增加，MPCs可见光透光率的峰值会相应增多，曲线也明显变宽。当周期数大于4以后，随周期数增加，MPCs可见光透光率曲线不再明显变宽，最大可见光透光率也相应降低。金属膜越厚，可见光透光率随周期数增加降低越快。

(3)随入射角度增加，MPCs透光率和反射率的中心波长都发生明显的蓝移，可见光透光率相应降低，而反射率相应提高。当入射角度小于60°时，可见光透光率随入射角增大下降较小。当入射角度大于60°时，MPCs可见光透光率明显降低。

(4)当MPCs的周期较大时，在光学频段会出现结构禁带，进而抑制相应波段的可见光在MPCs中传播。