BaGd2ZnO5∶Sm3+微晶粉末发光特性及其Judd-Ofelt分析

朱 婷，牛春晖

(北京信息科技大学 仪器科学与光电工程学院，北京 100192)

1 引言

近年来，稀土离子掺杂上转换材料已广泛应用于红外光探测、短波激光、生物荧光标记等[1-5]领域。因此，提高稀土材料的上转换发光效率非常重要。传统观点认为多声子弛豫是导致激发态的无辐射跃迁以及较低的上转换发光效率的主要因素[6-7]，而基质材料的声子能量越低，稀土离子发生多声子弛豫的几率越低。

作为基质材料，硫化物和氟化物的声子能量较低，但它们的化学稳定性相对较差。由于主晶格的拉伸振动，氧化物的声子能量相对较高，一般大于500 cm-1，而作为氧化物基质之一，BaGd2ZnO5具有较低的声子能量(大约为360 cm-1)[8-10]，可以保持多声道松弛并有利于交叉松弛过程。三价Sm3+离子是一种重要的稀土离子，它具有非常丰富的能级，可以在这些能级之间产生许多高效的发光[11-14]。因此，利用Sm3+离子开发新型光学和激光材料具有很大的潜力。

Judd-Ofelt(J-O)理论已被广泛用于计算玻璃态和晶态主体中稀土离子的光谱强度参数[15-16]。J-O理论提供了在特定精度内分析晶体结构的可能性[17-19]。以Ωt(t=2,4,6)表示的J-O强度参数对于评估激光介质和上转换器材料的性能至关重要。参数Ω2反映稀土离子所处局部晶场的结构和共价程度，此外，两个参数Ω4,6取决于长程效应并反映材料的整体性质。但对于许多微晶粉末材料，由于难以获得折射率、掺杂浓度和吸收率等基本计算参数，因此无法利用J-O理论研究其光谱性质。

据我们了解，本文是首次使用J-O理论研究BaGd2ZnO5微晶粉末中Sm3+离子的光谱特性。首先，采用高温固相法制备了5份具有不同Sm3+浓度的BaGd2ZnO5∶Sm3+微晶粉末样品，并通过X射线衍射(XRD)图谱分析了它们的相的组成。其次，通过测量微晶粉末样品的漫反射谱计算得到了吸收谱，并通过J-O理论计算光谱特征。第三，测量并分析了发射峰在610 nm处的激发光谱。然后，研究了所制备的样品在410 nm激发下的发射光谱，得到了发射峰强度与Sm3+离子掺杂浓度的关系。通过研究570，610，660 nm处的发光强度随Sm3+的掺杂浓度变化，发现了Sm3+发光的浓度猝灭现象，根据能量转移理论的分析结果表明，Sm3+离子中的浓度猝灭机制属于偶极-偶极相互作用。最后，计算并讨论了5个样品的CIE颜色坐标。

2 实验

2.1 材料准备

按照量比称取5份质量为10 g的原料，分别为BaCO3∶ZnO∶Gd2O3∶Sm2O3=100∶105∶100-x∶x(x=0.5,1,2,4,8)。在这些原料中，多余的5%ZnO是为了补偿ZnO高温分解产生的Zn离子流失，Gd2O3和Sm2O3是光谱纯试剂，BaCO3和ZnO是分析纯试剂。

将5份原料依次在玛瑙研钵中研磨并混合均匀，然后放入5个10 mL小陶瓷坩埚中。准备5个100 mL大陶瓷坩埚并在其中放置适量的ZnO粉末，将5个10 mL小陶瓷坩埚分别置于100 mL大陶瓷坩埚中，并在10 mL小陶瓷坩埚外罩上30 mL中陶瓷坩埚。将5个大陶瓷坩埚放入马弗炉中，在1 200 ℃下煅烧4 h，然后取出并自然冷却至室温。将冷却的样品再次研磨并封装在5个样品袋中用于下一次测量。准备好的5份样品分别编号为1#(x=0.5)、2#(x=1)、3#(x=2)、4#(x=4)和5#(x=8)。

2.2 材料特性测试

采用日立DMAX-3A型X射线衍射仪(XRD)进行物相分析，扫描范围为10°～80°(Cu靶，λ=0.154 06 nm)。

使用Zolix Omi-λ150型单色仪、Omi-λ300单色仪和PMTH-S1-CR131光电倍增管测量激发光谱和发射光谱。

使用Avantes ASPHERES-50-LS-HAL-12V积分球和AvaSpec-2018光纤光谱仪测量漫反射光谱，I(λ)和I0(λ)分别代表纯BaGd2ZnO5和Sm3+掺杂的BaGd2ZnO5微晶粉末的漫反射光谱。BaGd2ZnO5和Sm3+微晶粉末的吸收光谱通过公式α(λ)=-ln[R(λ)]推导得出，这里，ln[]表示自然对数[20]。

3 J-O光谱特性理论

Judd[15]和Ofelt[16]发明了关于稀土离子跃迁强度的独立定性计算方法，称为J-O理论。

在J-O理论中，电偶极子跃迁的强度可以表示为：

Sed=∑Ωt|<4fNψJ‖U+‖4fNψ′J′>|2

(t=2,4,6)，

(1)

这里，‖U+‖是单位张量算子，约化矩阵元为|<4fNψJ‖U+‖ 4fNψ′J′>|2，与稀土离子的种类和跃迁能级有关但与主体介质无关，Ωt是谱线强度参数，与主体介质中稀土离子的晶格位置有关。

电偶极跃迁的实验振子强度可表示为：

(2)

磁偶极跃迁的谱线强度可表示为：

Smd=

(3)

这里|<4fNΨJ‖L+2S‖4fNΨ′J′>|2是磁偶极子跃迁的矩阵元素减少，磁偶极子跃迁的谱线振荡器强度可以表示为：

(4)

对于稀土离子的两个相邻能级之间的光谱跃迁，实验振子强度可以表示为电偶极振子强度和磁偶极振子强度的总和，即fexp=fed+fmd。

实验振子强度与每个光谱吸收峰的积分量有如下关系：

(5)

其中，e是电子的电量；N是稀土离子的剂量浓度(单位：cm-3)；k(λ)是光密度，它与吸收系数α(λ)的关系为：

(6)

其中l是主介质中的光程长度。

根据公式(1)、(2)和(5)，光谱强度参数Ωt可以通过对吸收光谱的平方拟合来获得。

理论振子强度可表示为：

(7)

能级跃迁的自发跃迁几率是电偶极矩跃迁几率和磁偶极矩跃迁几率之和，可用下式表示：

AJJ′=Aed+Amd=

从能级ΨJ到Ψ′J′的跃迁分支比为：

β[J，J′]=AJJ′/[∑J′AJJ′]，

(9)

能级ΨJ的寿命等于从ΨJ到其所有较低级别的自发跃迁几率之和，即：

τ=1/[∑J′AJJ′].

(10)

4 结果与讨论

4.1 XRD图谱与分析

样品测试得到的XRD图如图1所示。从图1中可以看出，样品的主要XRD峰与PDF 49-0518中晶体BaGd2ZnO5的X射线衍射峰一致，说明BaCO3、ZnO和Gd2O3反应完全生成了BaGd2ZnO5。

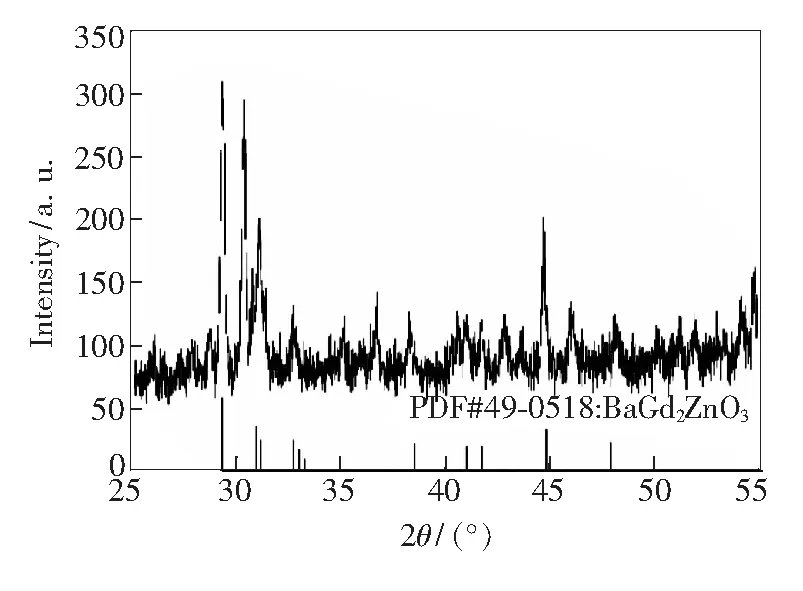
图1 样品5#的XRD图谱Fig.1 XRD pattern of sample 5#

4.2 吸收光谱与J-O计算

通过前面叙述的测量方法，测量了制备的样品5#的吸收光谱，如图2所示。

从图2可以看出，在380～1 800 nm的光谱范围内，Sm3+离子有许多突出的吸收峰，相应的激发态能级如图2所示。图中位于1 070 nm附近的强吸收峰对应于从6H5/2到6F9/2的跃迁，所以它经常用于吸收滤波器，吸收1 064 nm波长的激光[21]。

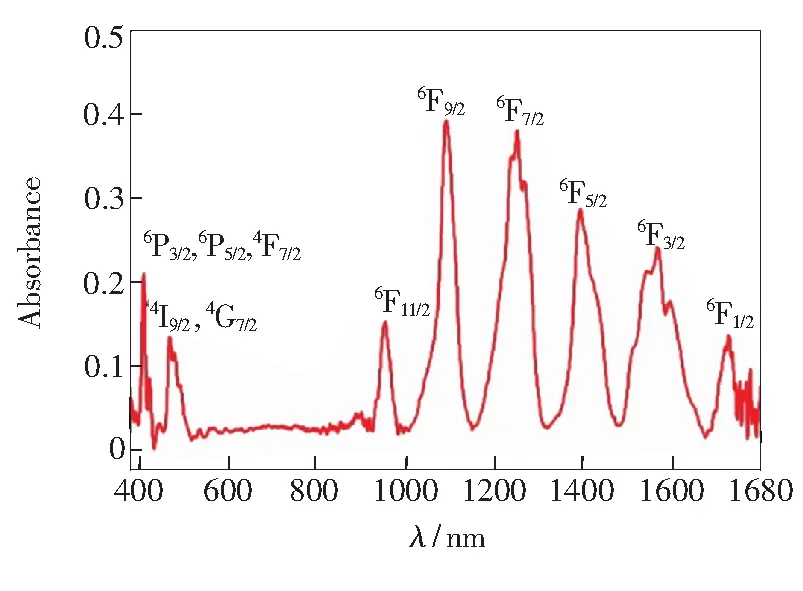
图2 样品5#的吸收光谱Fig.2 Sample 5# absorption spectrum

对于粉末样品而言，它的折射率n、离子掺杂浓度N和光学吸收长度d并不能直接得出。根据参考文献[22]，粉末主体材料的折射率n可以通过发射光谱和掺杂在粉末主体材料中的Eu3+离子的5D0寿命推导出。

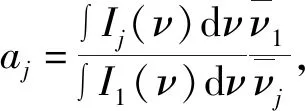
如果已知折射率n′和磁偶极子跃迁概率A′1，则粉末主体材料的折射率n可表示为n=n′(A1/A′1)1/3。

制备了Eu3+掺杂的BaGd2ZnO5粉末材料，并测量了其发射光谱和5D0能级Eu3+离子的寿命。每个发射峰的比例系数、5D0寿命和计算的折射率列于表1中。

表1 每个发射峰的比率系数、5D0寿命和计算的折射率Tab.1 Ratio coefficient for each emission peak,5D0 lifetime and calculated refractive index

在表1中，Eu3+掺杂的LaF3晶体的相对数据来自参考文献[23]。可以看出BaGd2ZnO5粉末主体材料的折射率为2.31。

此外，根据参考文献[24]，采用多次漫反射法的模拟结果表明，粉末材料中的光程与折射率成比例，并且光程长度在1.1～2.4的折射率范围内增加15%。分别测量了Sm3+掺杂硼硅酸盐玻璃的吸收光谱和研磨粉末的漫反射光谱，确定了硼硅酸盐玻璃粉末的一定厚度h，其吸收率与2.70 cm厚的硼硅酸盐玻璃相同。在本文中，通过使Sm3+掺杂的BaGd2ZnO5粉末样品的厚度等于h来测量图2中所示的吸收光谱。考虑到BaGd2ZnO5粉末(n=2.31)对硼硅酸盐玻璃粉末(n=1.7)的光程长度有6.5%的修正，实际光程长度为d=2.70 cm×(1+6.5%)≈2.875 cm。

从XRD数据推导出离子掺杂浓度N。掺杂Sm3+的BaGd2ZnO5微晶粉末样品的3个参数如下：n=2.31，N=3.04×1020cm-3，d≈2.875 cm。使用图2中所示的吸收光谱计算BaGd2ZnO5微晶中Sm3+的光谱强度参数：Ω2=0.43×10-20cm2,Ω4=0.17×10-20cm2，Ω6=0.27×10-20cm2。

计算了图2所示几个吸收峰对应的实验和理论振子强度，如表2所示。实验和理论振子强度之间的差异可表示为：

δrms=[∑(Δf)2/(Ntran-Npara)]1/2，

(11)

其中，∑(Δf)2是实验和理论振荡器强度之间的偏差的平方和，Ntran是观察到的由吸收引起的能级跃迁的数量，Npara是计算参数的数量。

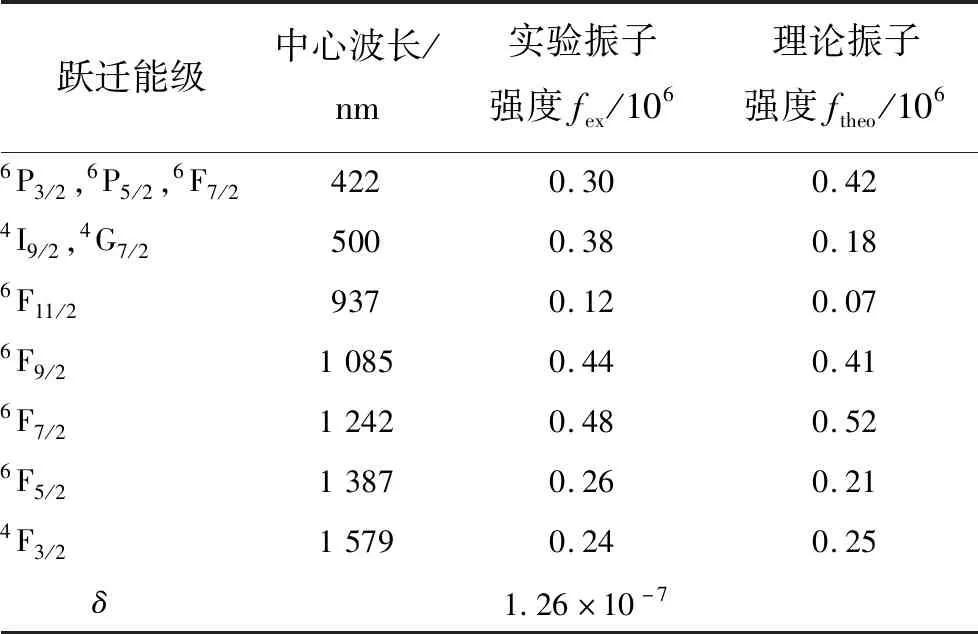
表2 实验和理论振子强度Tab.2 Experimental and theoretical vibrator strength

从表2中可以看出，实验振子强度与理论振子强度的值差别很小，偏差为δrms=1.26×10-7。

由公式(8)可以看出，当掺杂离子相同、基质材料不同时，磁偶极矩跃迁几率的比值等于两物质的折射率的比的三次方，可表示为：

(12)

根据参考文献[25]中LaF3∶Sm3+主体粉末的折射率为1.58以及其4G5/2能级跃迁到其他能级的磁偶极矩跃迁几率，由公式(12)即可以得出BaGd2ZnO5微晶粉末中Sm3+离子的磁偶极矩跃迁几率。使用J-O理论,计算BaGd2ZnO5微晶粉末中Sm3+离子的电偶极矩跃迁几率、跃迁分支比和能级寿命，结果如表3所示。

表3 Sm3+的跃迁几率、跃迁分支比和能级寿命Tab.3 Sm3+ transition probability,transition branch ratio and energy level lifetime

从表3中可以看出：

(1)4G5/2能级的寿命较长，为4.82 ms，可用作激光发生过程的上能级；

(2)4G5/2到6H9/2和4G5/2到6H7/2的跃迁几率和跃迁分支明显高于其他跃迁，这意味着在Sm3+发射光谱中610 nm和660 nm处会有两个强发射峰。

为了验证上述计算的有效性，在410 nm的激发下，通过660 nm处的发射强度衰减曲线拟合了Sm3+离子的4G5/2能级的寿命，如图3所示。在图3中，虚线表示实验数据，实线表示拟合数据。

根据指数衰减曲线实现拟合如下:

(13)

其中t1表示高能级的寿命。拟合结果表明4G5/2能级的寿命约为5.77 ms，接近表3中显示的计算寿命4.82 ms。

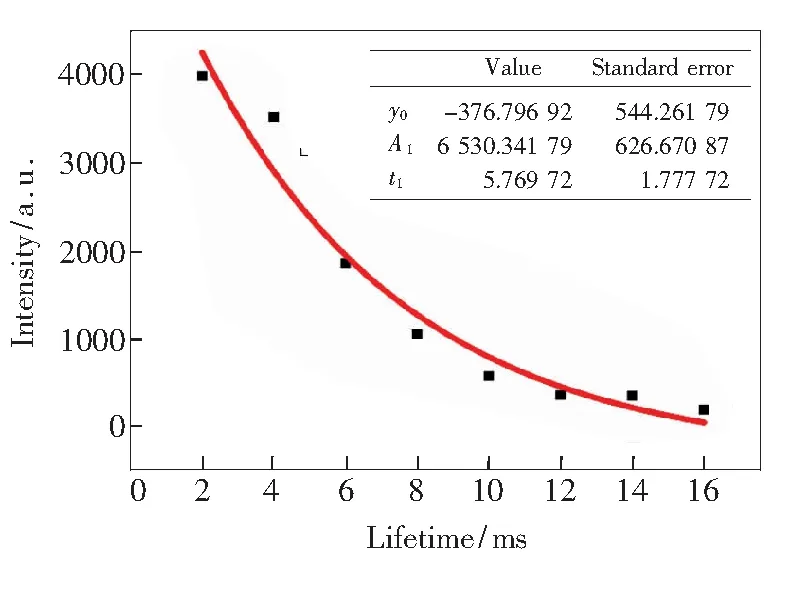
图3 5#样品的4G5/2级的寿命拟合Fig.3 Life fit of4G5/2 grade of 5# sample

4.3 激发谱和发射谱

检测了Sm3+的特征发射峰对应的波长(610 nm)处的激发光谱，如图4所示。从图4中可以看出，其中的激发峰是Sm3+离子的4f-4f能级跃迁。从左到右，激发峰对应于6H5/2到4P7/2、4L13/2(4F7/2)、4G9/2、4I11/2(4I13/2)和4F3/2的跃迁。最强激发峰位于410 nm。

图4 样品5#的激发光谱，发射波长为610 nm。Fig.4 Excitation spectrum of sample 5#,emission wavelength is 610 nm.

选择410 nm为激发波长，收集5个制备样品的发射光谱，如图5所示。很明显，5个样品有相似的发射峰。

为了定量研究发光强度与Sm3+的掺杂浓度之间的关系，绘制了570 nm(6H7/2→6H5/2)、610 nm(6H9/2→6H5/2)、660 nm(6H11/2→6H5/2)发射峰处发光强度与Sm3+的掺杂浓度的关系曲线，如图6所示。可以看出，随着Sm3+掺杂浓度的增大，570，610，660 nm处的发射强度均先增加后减小，并且当掺杂Sm3+离子浓度为1%时，强度出现最大值。发射峰强度的逐渐减弱，归因于高掺杂浓度下的浓度猝灭机制。

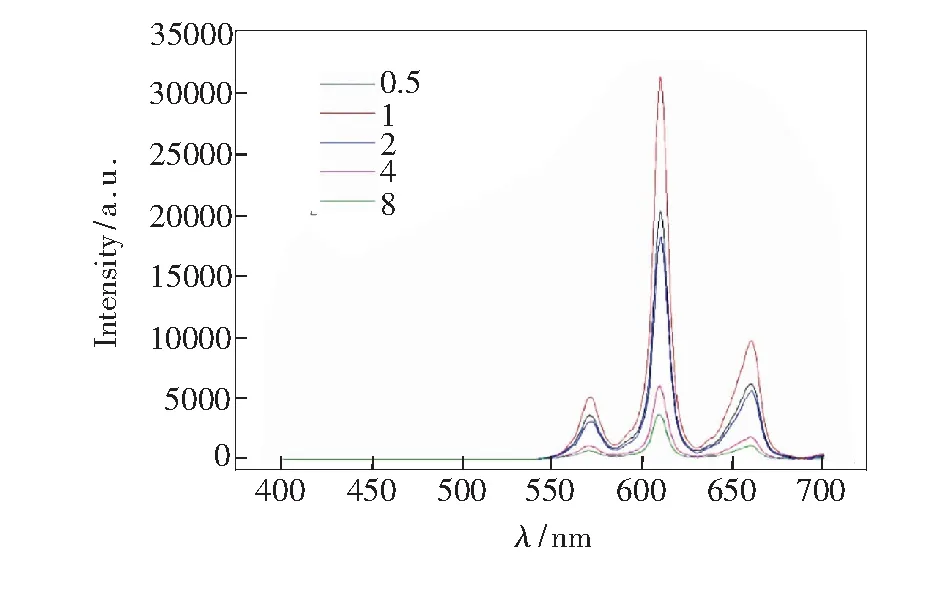
图5 在410 nm激发的5个样品的发射光谱Fig.5 Emission spectra of five samples excited at 410 nm

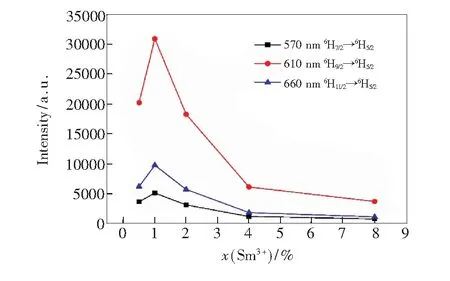
图6 发射峰强度与Sm3+的掺杂浓度的关系曲线Fig.6 Relationship between emission peak intensity and doping concentration of Sm3+

根据Dexter理论[26]，在非导电无机材料中，活化剂离子的浓度猝灭机制属于电多极相互作用。当荧光粉中活化剂离子的掺杂浓度足够大时，发光强度与活化剂离子的摩尔分数有关：

lg(I/x)=c-klgx，

(14)

其中，I是发光强度，x表示活化剂离子的摩尔分数，k是比例系数，c是常数。当电多极相互作用是偶极-偶极、偶极-四极或四极-四极时，k等于2.00,2.67或3.33。

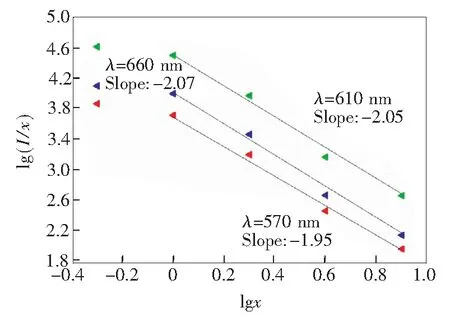
图7 lg(I/x)和lgx的关系曲线Fig.7 lg(I/x)and lgx curve

lg(I/x)和lgx的关系曲线如图7所示。虚线表示拟合曲线，很明显3条拟合曲线的斜率分别为-2.05(波长为610 nm的发光峰值)，-2.07(波长为660 nm的发光峰值)和-1.95(波长为570 nm的发光峰值)，k值分别为2.05,2.07,1.95。这意味着Sm3+离子从6F11/2到6F1/2过渡发射的浓度猝灭机制属于偶极-偶极相互作用。

4.4 CIE色坐标计算

为了研究制备的样品的发光性能，将发射谱的数据导入CIE1931xy软件计算在410 nm激发的5个制备样品的发射光谱的CIE色坐标，如表4所示。

表4 在410nm激发下BaGd2ZnO5∶Sm3+磷光体的CIE色坐标Tab.4 CIE color coordinates of BaGd2ZnO5∶Sm3+ phosphors at 410 nm excitation

从表4可以看出，CIE坐标随着Sm3+离子的掺杂浓度而变化，样品的CIE坐标均在橙红区域。通过计算，样品5(Sm3+掺杂浓度为0.08)的CIE坐标离白光区域最近。

5 结论

通过常规固相法在1 200 ℃恒温4 h制备了不同掺杂浓度的Sm3+的BaGd2ZnO5的微晶粉末。X射线衍射图表明制备的化合物充分结晶。测量了样品的漫反射谱并推导得到吸收谱，还通过J-O理论分析了光谱特性。根据吸收谱计算得到样品的谱线强度参数Ωλ(λ=2,4,6)，从而计算出理论振子强度和实验振子强度，其偏差为δrms=1.26×10-7。计算了Sm3+的4G5/2能级到所有下能级跃迁的电偶极矩跃迁几率、磁偶极矩跃迁几率、跃迁分支比及4G5/2能级寿命参数。发现4G5/2能级的寿命较长，为4.82 ms，可用作激光发生过程的上能级；4G5/2到6H9/2和4G5/2到6H7/2的跃迁几率和跃迁分支明显高于其他跃迁，这意味着在Sm3+发射光谱中610 nm和660 nm处会有两个强发射峰。测量了发射波长为610 nm的激发光谱，发现了由于Sm3+离子的4f-4f跃迁引起的6个激发峰。测量了在410 nm激发的发射光谱，验证了Sm3+发射光谱中610 nm和660 nm的两个强发射峰。通过研究570，610，660 nm处的发光强度随Sm3+的掺杂浓度变化，发现了Sm3+发光的浓度猝灭现象，根据能量转移理论的分析结果表明，Sm3+离子中的浓度猝灭机制属于偶极-偶极相互作用。计算了制备样品的CIE色坐标，结果表明所有坐标位于橙红区域。