Voigt线型宽度的经验公式及其应用

2019-08-21尹增谦袁春琪王永杰

发光学报 2019年8期

尹增谦，袁春琪，王永杰

(华北电力大学数理系，河北保定 071003)

1 引言

由于光谱线型中包含有发光粒子的内部结构、粒子间相互作用、周围环境等信息，光谱线型的研究在化学反应动力学、气象学、宇宙学等研究领域有很重要的理论意义和应用价值[1-9]。在低气压情况下，谱线的展宽是多普勒展宽占主导地位，而在压强很高的情况下，发光粒子与其他粒子频繁碰撞产生的碰撞展宽占优势。在实际发光系统中，两种展宽机制都是存在的，光谱线型为综合展宽线型。此时对应的线型函数是洛仑兹线型和高斯线型函数的卷积形式，称为Voigt线型函数。

自Voigt线型谱线提出以来，对它的研究一直备受重视[2-4]，本工作在分析洛仑兹线型函数和高斯线型函数的基础上，系统研究了Voigt线型函数，得到了三者谱线半宽度的经验公式。利用这个经验公式，建立了由实验线型函数获得洛仑兹、高斯线型函数的计算方案。

2 三种展宽线型函数

2.1 洛仑兹线型函数

由于自发辐射和碰撞而导致的均匀展宽线型函数，称为洛仑兹线型函数，其形式为[2]：

(1)

其中，ν0、αL分别为中心频率和半宽度，显然洛仑兹线型函数的最大值为：

(2)

2.2 高斯线型函数

当发光粒子有运动速度分布时，由多普勒效应引起的频移，会导致光谱线型为如下的高斯线型函数[2]：

(3)

对应的半宽度αG为：

(4)

公式(3)、(4)中ν0为中心频率，m、T分别为发光粒子的质量和气体温度，k、c分别为玻耳兹曼常数和真空中的光速。显然高斯线型函数的最大值为：

(5)

2.3 Voigt线型函数

对于气体工作物质，上述由碰撞导致的均匀展宽和多普勒效应导致的非均匀展宽是主要的展宽类型，气体工作物质是由这两种展宽机制综合作用的，得到综合展宽线型函数为如下卷积形式的Voigt线型函数：

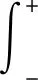
(6)

根据傅里叶变换的乘积定理，可以得到Voigt线型函数的最大值为[2]：

(7)

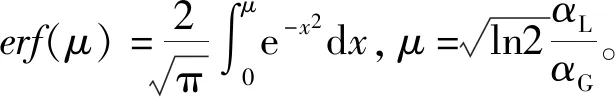
3 Voigt函数线宽的经验公式

如上所述，实验获得的光谱线型函数，即Voigt线型函数是由公式(6)决定的，但如何由gV(ν,ν0)得到与其对应的αL、αG这两个包含有发光粒子内部结构和周围环境信息的物理量，是具有重要意义的工作。

由实验获得的gV(ν,ν0)，可以得到gV,max和其半宽度αV，如果能得到Voigt线型函数半宽度αV与对应的αL、αG的关系式αV=f(αL,αG)，则将该关系式与公式(7)联立，就构造了关于αL、αG的二元方程组，解该方程组即得到αL、αG。

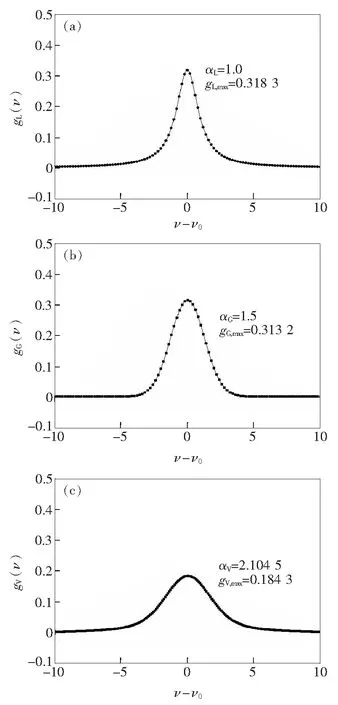
图1 3种线型函数图。(a)洛仑兹线型函数；(b)高斯线型函数；(c)Voigt线型函数。Fig.1 Three line shape function diagrams.(a)Lorentz line shape function.(b)Gaussian line shape function.(c)Voigt line shape function.

由于公式(5)没有更便于计算的解析形式，所以，可以给定一组αL、αG值，用数值积分的方法求出公式(6)中的gV(ν,ν0)，从而得到其半宽度αV，如图1所示。由大量的(αLi,αGi)→αVi数值，就可建立经验公式αV=f(αL,αG)。

我们进行了大量的数值计算即得到大量的(αLi、αGi、αVi)值，并假设经验公式为：

(8)

其中b为待定系数。

为了得到上述经验公式中的b，记

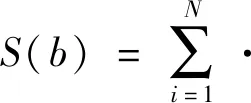
显然，当S(b)取得最小值时的b即为最佳的系数。令

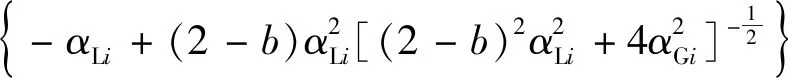
(10)

由数值求解公式(10)，得到b=1.063 8。所以3种线型半宽度之间的经验公式为：

为验证上述经验公式的可靠性，我们把由公式(6)计算的(αLi、αGi、αVi)与用经验公式(11)计算的αV进行了比较，如图2所示，图2中线表示经验公式，点表示公式(6)计算的值，可以看出二者吻合很好。

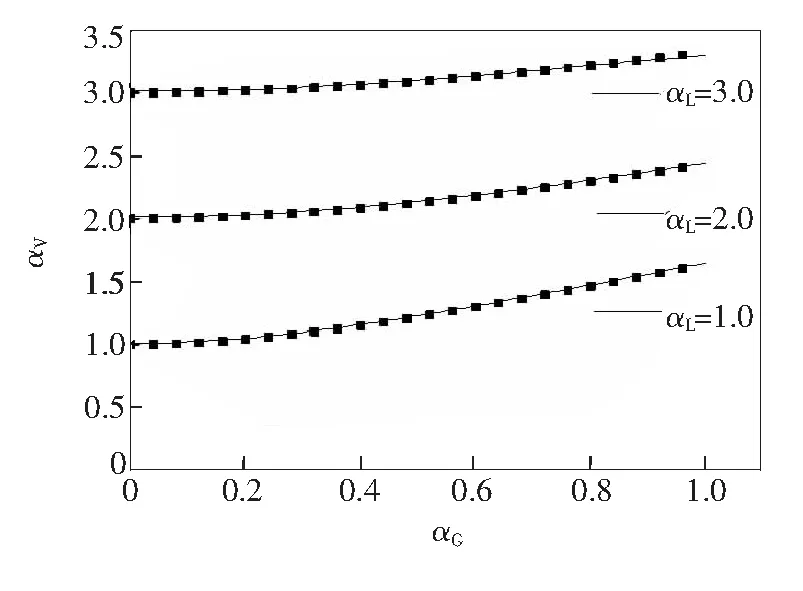
图2 经验公式与精确值的比较(线表示经验公式，点表示精确值)Fig.2 Comparison of empirical formulas with exact values (lines represent empirical formulas,points represent exact values)

4 经验公式的应用

光谱线型中包含有发光粒子物理性质的信息如电子密度、气体温度等，但是由实验上获得的Voigt线型函数，不能直接得到αL、αG，从而不能直接得到发光等离子体电子密度气体温度等信息。

根据本工作得到的经验公式(11)和最大值公式(7)，得到如下方程组：

(12)

解该方程组，可以由Voigt线型的最大值Vmax及半高全宽ΔV得到αL、αG。

需要指出的是，在解方程组(12)时，误差函数erf(x)可以从参考文献[10-11]查到x=[0,5]范围内的值，但是，对于x>5.0的erf(x)的值，虽然经过大量调研，但并没有查到。我们采用由下式替换公式(7)的方法解决[2]：

(13)

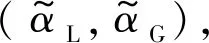
图3 由Voigt线型函数得到的洛仑兹和高斯线型函数。(a)Voigt线型函数；(b)洛仑兹线型函数；(c)高斯线型函数。Fig.3 Lorentz and Gaussian line shape functions obtained from Voigt line shape function.(a)Voigt line shape function.(b)Lorentz line shape function.(c)Gaussian line shape function.

为了说明由实验获得的光谱线求其对应的αL、αG的计算过程，我们给出一条实验谱线并对其进行了计算。实验采用文献[12]中的实验装置，实验参数为：取双铜片电极，电极间距为10 mm，接地极距离管口10 mm，两铜片宽度均为13 mm，氩气的流量为1 L/min，电压9.8 kV，采集的光谱为P点处。采集的是氩等离子体射流的发射光谱。图4(a)为氩等离子体射流图片及光谱采集位置，图4(b)为采集的光谱。

图4 (a)氩等离子体射流图片及光谱采集位置图;(b)Ar I 696.5 nm的发射光谱。Fig.4 (a)Argon plasma jet image and spectral acquisition position.(b)Emission spectrum of Ar I 696.5 nm.

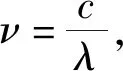
(14)

由上述两种光谱线型函数的转化关系即公式(14)以及归一化条件，我们可以把图4(b)的696.5 nm的氩发射光谱转化成归一化的图5。

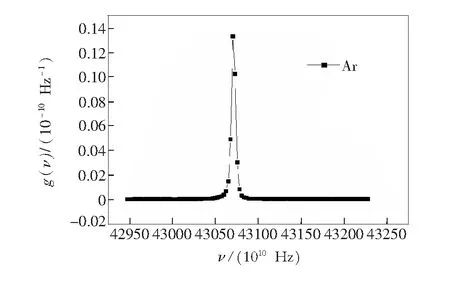
图5 Ar I 696.5 nm的发射光谱Fig.5 Emission spectrum of Ar I 696.5 nm

由图5谱线可以得到Voigt线型函数的Vmax=1.33×10-11Ηz-1、αV=3.48×1010Ηz。解方程组(12)求得αL=1.400×109Ηz，αG=3.402×1010Ηz，该Voigt线型函数对应的洛仑兹和高斯线型函数如图6所示。

图6 由Voigt线型函数得到的洛仑兹和高斯线型函数。(a)洛仑兹线型函数；(b)高斯线型函数。Fig.6 Lorentz and Gaussian line shape functions obtained from Voigt line shape function.(a)Lorentz line shape function.(b)Gaussian line shape function.