铁路道岔转辙器部件轮轨两点接触计算方法研究
2019-08-20马晓川徐井芒胡辰阳
马晓川, 徐井芒, 王 平, 陈 漫, 胡辰阳, 王 健
(1. 华东交通大学 铁路环境振动与噪声教育部工程研究中心, 江西 南昌 330013;2. 西南交通大学 高速铁路线路工程教育部重点实验室, 四川 成都 610031)
铁路列车通过道岔尖轨的往复扳动实现转线运行,单开铁路道岔主要由转辙器、辙叉及连接部分组成。相比区间线路,沿道岔线路纵向,钢轨变截面、多股钢轨轨下基础布置方式各异,导致其轮轨接触状态较为复杂[1],是导致道岔轮轨冲击作用较大的主要原因,严重时会引发钢轨磨耗及裂纹等多种伤损。
在铁路道岔转辙器部件中,由于尖轨和基本轨的轨下基础布置方式不同,车轮通过转辙器部件时,在车轮荷载的作用下,尖轨和基本轨之间势必会发生相对运动,尖基轨的相对运动会对轮轨接触状态会产生较大的影响。因此,王平[2-3]分析了车轮荷载作用下的轮轨接触行为,建立了道岔转辙器内车轮荷载分配的求解模型,并结合试验结果验证模型的正确性,该方法虽然考虑了尖轨与基本轨的相对运动,但限定车轮为锥形踏面,且轮轨接触点位置为尖轨和基本轨的最高点,而目前车轮大多为磨耗型踏面,因此该方法存在一定的局限性。Xu等[4]将车辆道岔多体动力学中的计算结果导入有限元模型中,来研究细部的轮轨接触关系,在其建立的有限元模型中,能够考虑尖轨和基本轨的相对运动,但有限元模型计算时间过长,研究效率较低。以往的铁路道岔轮轨接触研究中,均将尖轨与基本轨视为刚性组合,即认为两者之间不会发生相对运动。其中,任尊松等[5-7]根据轮轨弹性接触变形量与轮轨间隙之间的关系,提出了车轮与道岔钢轨发生多点接触的判别方法,并基于此,建立车辆-道岔系统动力学模型,用于研究车轮与道岔钢轨的横向和垂向耦合振动问题。在中频振动条件下,Afli等[8]提出了可考虑轮轨多点接触的车辆-道岔动力响应求解方法,并分析了轨道弹性变化对轮轨动态响应的影响规律。采用节点方法,Sugiyama等[9]提出非共形接触组合算法来研究道岔区轮轨接触状态。为进一步提升车辆-道岔动力学的仿真精度,Sebes等[10]在这一过程中采用非赫兹理论模拟轮轨之间的滚动接触行为,相比赫兹理论,采用非赫兹接触方法能够获取更为准确的轮轨滚动接触信息,如接触斑形状、接触应力等。为评估不同轮轨接触模型在求解道岔区轮轨接触问题时的适用性,Xu等[11]比较了赫兹理论、非赫兹理论、Kalker三维接触理论及有限元方法的仿真结果,并认为结合计算精度与效率,非赫兹理论更能反映车轮与道岔钢轨的滚动接触行为。文献[5-11]均假设尖轨和基本轨的相对位置保持不变来研究车轮与道岔钢轨的接触状态,而实际上,尖轨与基本轨的轨下支撑方式存在较大差异,在车轮荷载作用下,两者必然会发生相对位置的改变,并影响轮轨之间的接触状态,因此,需在考虑尖轨与基本轨相对运动的基础上,研究车轮与转辙器钢轨的滚动接触问题。
本文根据基本轨与尖轨的相对位置及轨下支撑方式,分析车轮与转辙器钢轨的接触特性,并提出了考虑尖轨和基本轨相对运动的轮轨两点接触计算方法,以中国18号单开高速道岔为例,对比分析了标准和磨耗车轮LMA踏面与钢轨匹配时的轮轨接触特性,包括轮轨接触点位置、轮轨两点接触可能发生的区域以及静态轮载转移和分配的规律。
1 转辙器部件轮轨接触状态
在铁路道岔转辙器部件内,尖轨与基本轨会共同承担车轮荷载,并且尖轨为变截面钢轨部件,导致轮轨接触关系复杂多变。在该区域内,理论上的轮轨接触状态有以下6种:车轮与基本轨或尖轨发生单点接触见图1(a)、图1(f);车轮与基本轨或尖轨发生踏面、轮缘位置处的两点接触见图1(b)、图1(e);车轮与尖轨、基本轨的两点接触见图1(c);车轮与尖轨、基本轨的三点接触见图1(d)。
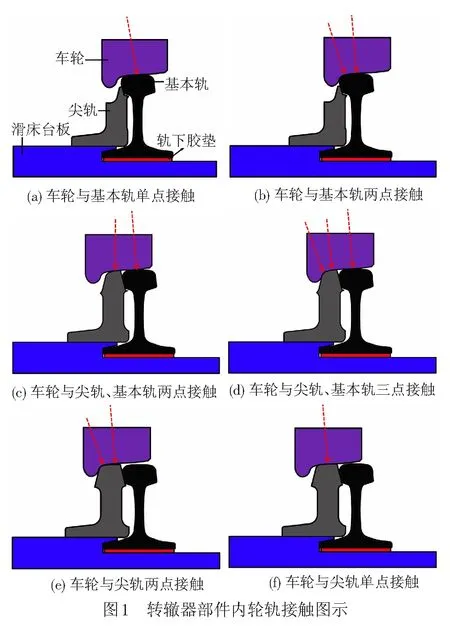
在车轮运动状态下,图1(a)、1(c)、1(f)所表示的轮轨接触状态是较为普遍的,图1(d)所表示的轮轨三点接触状态很难发生[7],当轮对的横向位移较大,车轮轮缘与钢轨接触时,图1(b)和1(e)表示的轮轨两点接触状态才存在理论上发生的可能。综上,本文将只针对图1(a)、1(c)、1(f)所代表的轮轨接触状态进行研究,即轮轨单点接触时,车轮分别只与基本轨或尖轨接触,轮轨两点接触时,车轮同时接触基本轨和尖轨。
如图1(a)所示,以滑床板上表面为基准,尖轨与滑床板之间为刚性约束,即尖轨承受车轮荷载时不会发生相对滑床板的垂向刚性位移。基本轨与滑床板之间为扣件系统中的橡胶垫板,在车轮荷载作用下,以滑床板为基准,基本轨会发生相对尖轨的垂向位移,从而对轮轨接触状态会产生较大影响,在轮轨接触状态的判定中应给予充分的考虑。
2 轮轨接触状态判定方法

根据车轮和钢轨的空间位置约束关系,使用迹线法[12-14]来求解轮轨的接触几何参数,在距尖轨尖端x的断面处,使用迹线法迭代求解轮轨接触参数。轮对横移为yw见图2,先将尖轨和基本轨的廓形数据合并作为一个轨头廓形进行计算,在迭代求解轮轨接触参数的过程中,首先求解左右车轮与对应两股钢轨之间的垂向最小距离dl和dr,通过调整轮对的侧滚角θ,当dl和dr的关系满足式(1)的要求,可得到左右侧轮轨接触点的位置以及相应的轮轨接触参数。Oxyz为轨道中心坐标系,O′x′y′z′为轮对中心坐标系。
|dl-dr|<ε
( 1 )
式中:ε为给定的无限小的数值,本文取10-5mm。
在满足式( 1 )的条件下,保持轮轨侧滚角不变见图3,分别求解右侧车轮到尖轨、基本轨的最小距离dsw和dst,右侧轮轨的最小距离dr=min(dsw,dst),若dr=dsw,则dsw对应的位置为主接触点位置,dst对应的位置为次接触点位置,同理,若dr=dst,则dst对应的位置为主接触点位置,dsw对应的位置为次接触点位置。图2和图3中的最小距离均采用三次样条函数的方法进行拟合和插值计算。
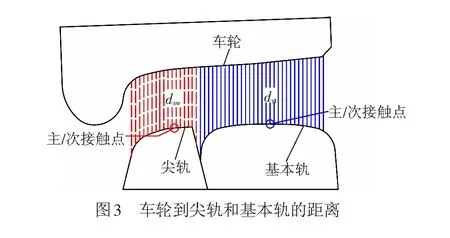
定义车轮踏面与主次接触点之前最小距离的差值hwr计算式为
hwr=dsw-dst
( 2 )
车轮与两股钢轨的接触状态判别条件为
基本轨单点接触
hwr≥wst,P+δst,P
尖基轨两点接触
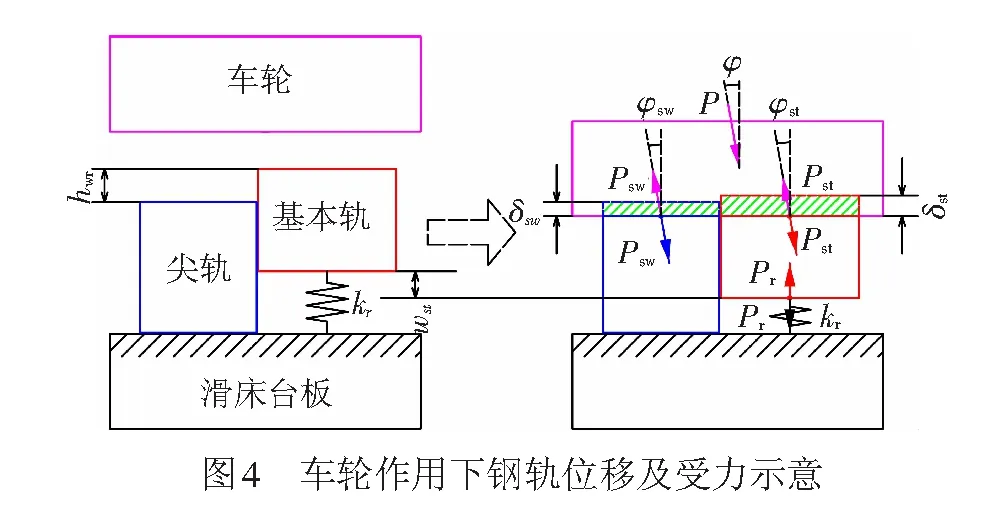
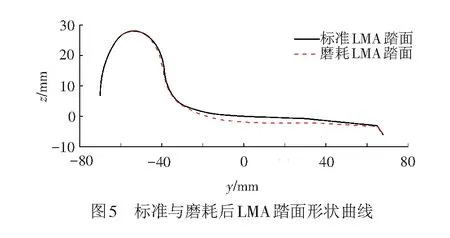
-δst,P 尖轨单点接触 hwr≤-δst,P ( 3 ) 式中:在全部车轮荷载作用下,以滑床板为基准,wst,P为基本轨的垂向刚性位移;δst,P为车轮与基本轨接触时的垂向轮轨压缩量;δsw,P为尖轨的垂向轮轨压缩量。 本文假设钢轨的垂向刚性位移仅由轮轨垂向力引起,钢轨的横向和扭转运动不影响钢轨的垂向刚性位移,基本轨垂向刚性位移的计算式为 wst,P=P·cosφ/kr ( 4 ) 式中:P为车轮荷载;φ为主接触点处的轮轨接触角;kr为基本轨轨下胶垫的垂向刚度。 车轮与钢轨接触时的压缩量与轮轨法向力密切相关,基本轨或尖轨承受全部车轮荷载时,其垂向压缩量可简单算出为[15] ( 5 ) 式中:Gst、Gsu分别为车轮与基本轨接触点处、车轮与尖轨接触点处的赫兹接触参数,m/N2/3;φst为车轮与基本轨接触点处的车轮接触角;φsw为车轮与尖轨接触点处的车轮接触角。 锥形踏面 G=4.57R-0.149×10-8 磨耗型踏面 G=3.68R-0.115×10-8 ( 6 ) 式中:G为不同踏面形式的赫兹接触参数,N2/3;R为接触点处车轮的滚动圆半径,对于不同的接触点位置,其滚动圆半径各不相同。 车轮与基本轨或尖轨发生单点接触时,其轮轨法向力可通过轮轨相互作用力和接触角度进行计算。而当车轮与尖轨、基本轨同时接触时,由于尖轨与基本轨的相对运动,导致两个接触点处轮轨法向力的求解较为复杂,本文根据作用力与位移的协调关系,给出求解尖轨和基本轨上接触点处轮轨法向力的方法。尖轨和基本轨在车轮荷载作用下发生变形的过程见图4。基本轨与尖轨的相对运动主要发生在垂向,在图4所示的力学模型中,基本轨与尖轨之间的垂向约束关系较弱,因此,两股钢轨之间的相互作用可忽略不计。 由图4可知,基本轨和尖轨之间的位移协调关系可表达为 wst+(δst-δsw)=hwr ( 7 ) 基本轨发生的垂向刚性位移为 w=Pr/kr ( 8 ) 式中:Pr为轨下胶垫对基本轨的支撑力。 基本轨的垂向轮轨压缩量由式为 δst=Gst·cosφst·(Pst)2/3 ( 9 ) 式中:Pst为车轮与基本轨之间的法向轮轨力。 这节课结束以后,我又布置了这样一个课后作业:“茫茫”除了可以形容沙漠(茫茫的沙漠),还可以形容大海、草原、夜色、人海等。请你想象其中的一个画面并写一写,当然你也可以摘抄你读过的描写这些画面的原文。 尖轨的垂向轮轨压缩量为 δsw=Gsw·cosφsw·(Psw)2/3 (10) 式中:Psw为车轮与尖轨之间的法向轮轨力。 另外,根据基本轨自身的受力平衡为 Pr=Pst·cosφst (11) 同理,根据车轮自身的受力平衡为 P·cosφ=Pst·cosφst+Psw·cosφsw (12) 由式( 7 )~式(12)联立可得到求解车轮与基本轨接触点处法向力的函数为 (13) 式中:Pst∈(0,P)。 为证明函数f有唯一的解,首先证明式(13)所列函数存在零点,车轮与尖轨、基本轨发生两点接触时,hwr满足式( 3 )的条件,因此,函数f的两个端点值分别为 (14) 由式(14)可知,函数f(Pst)存在零点,对式(13)所列函数求导得到其一阶函数为 (15) 由式(15)可知,该函数为单调递增函数,综上,f(Pst)存在零点且为单调递增函数,即该函数有唯一解,使用数值方法求得该函数的解即为车轮与基本轨接触点处的法向力Pst,根据式(12)可求得车轮与尖轨接触点处的法向力Psw。 为验证本文所提铁路道岔转辙器轮轨两点接触计算方法的可行性,以中国直向通过速度250 km/h的18号高速道岔为例,对比分析标准和磨耗后LMA型踏面与尖基轨的接触匹配关系。标准和磨耗后LMA踏面的对比见图5,其中,磨耗后踏面形状为车辆运行15万km后的测试结果,与标准车轮踏面相比,该车轮踏面中部的磨耗深度较大,轮缘处则有轻微磨耗。 在判断车轮与尖轨和基本轨是否发生两点接触的过程中,需要车辆轨道系统振动过程中的轮轨法向力及反映轮对运动姿态的参数,但在研究轮轨匹配而不做动态计算时,可简单的以整车轴重(CRH2型车,140 kN)一半作为轮轨法向力的数值,判断不同轮对横移条件下的静态轮轨接触状态,轮对横移范围取0~12 mm,基本轨的轨下胶垫垂向刚度取270 kN/mm[16]。 在转辙器部件中,基本轨采用的是中国标准60 kg/m钢轨(CHN60),根据尖轨的加工方式,由尖轨的顶宽和降低值(图6)确定任意断面处尖轨的轨头廓形,并根据线路布置方式得到任意断面处尖轨和基本轨的空间位置关系,三个关键断面处尖轨与基本轨的空间相对位置见图7。 根据本文提出的车轮与尖基轨接触状态判断方法,分别计算尖轨顶宽25、30、35、40 mm断面处的轮轨接触点位置。标准踏面和磨耗后踏面与尖基轨的接触点位置分布情况见图8、图9。 由图8可知,标准车轮踏面与尖基轨匹配时,尖轨顶宽25 mm断面处,轮轨发生单点接触,不存在两点接触的可能,轮轨接触点位置主要分布在基本轨的轨顶上;在尖轨顶宽30 mm的断面处,轮轨只发生单点接触,而不存在两点接触的可能,轮轨接触点位置主要分布在基本轨的轨顶上;尖轨顶宽35 mm断面处,轮对横移在8.5~9.5 mm的范围内时,车轮同时与尖轨、基本轨接触,第2点接触的位置分布在尖轨轨距角附近;在尖轨顶宽40 mm断面处,轮轨只发生单点接触,不存在两点接触的可能,轮轨接触点位置主要分布在尖轨上,尖轨承受全部的车轮荷载。 由图9可知,磨耗车轮踏面与尖轨、基本轨匹配时,尖轨顶宽25 mm断面处,轮对横移在7.5~8 mm的范围内时,轮轨发生两点接触,第2点接触的位置分布在尖轨轨距角附近;在尖轨顶宽30 mm断面处,轮对横移在6.5~7 mm的范围内时,车轮与尖基轨发生两点接触,其第2点接触的位置分布在尖轨的轨距角附近;尖轨顶宽35 mm断面处,轮对横移在6~6.5 mm的范围内时,轮轨发生两点接触,第2点接触的位置分布在尖轨轨距角附近;尖轨顶宽40 mm断面处,轮对横移在4~4.5 mm的范围内时,轮轨发生两点接触,其第2点接触的位置分布在尖轨轨距角附近。 车轮与尖基轨发生两点接触的区域是车轮荷载在基本轨与尖轨之间完成转移的范围,轮载转移范围的位置会对轮轨横向动力相互作用产生较大的影响,轮载转移位置后移会增大轮对在道岔转辙器部件中蛇形运动的幅度,进而增大轮轨的动力相互作用[17]。由图8、图9对比可见,标准车轮踏面条件下,接触点位置在顶宽40 mm断面处已全部转移到尖轨上,而磨耗后车轮踏面匹配时,顶宽40 mm断面处仍有发生两点接触的可能性,且接触点位置分别集中在基本轨和尖轨上,会导致轮载转移位置后移,增大车辆与道岔之间的动态响应;其次,磨耗后车轮的轮轨接触点位置普遍位于尖轨的轨距角附近,会导致尖轨的侧面磨耗较为严重。综上,车轮踏面出现较大程度的磨耗后应及时进行镟修,以避免恶化高速道岔内的轮轨动力相互作用。 为探究转辙器部件内车轮与基本轨、尖轨发生两点接触的可能区域,沿道岔转辙器线路纵向,每隔0.01 m的距离选取一个断面,判断该断面处不同轮对横移情况下的接触状态,得到道岔转辙器部件范围内轮轨两点接触的可能区域见图10。 由图10可知,标准车轮踏面匹配时,距尖轨尖端5.87~6.90 m范围内可能发生轮轨两点接触,其轮轨两点接触的可能区域较为集中;磨耗后车轮踏面匹配时,距尖轨尖端3.61~7.75 m范围内均可能发生轮轨两点接触,其轮轨两点接触可能区域的分布较为分散,车辆轨道系统振动过程中,其轮轨接触状态容易在单点与两点接触之间切换,造成轮轨接触点的跳跃,影响轮轨接触关系的同时也会恶化轮轨动力相互作用。 车辆通过道岔转辙器部件时,随尖轨顶宽的变化,车轮由基本轨转移到尖轨或由尖轨转移到基本轨上,在轮载转移范围内,车轮与尖基轨发生两点接触,尖轨和基本轨共同承受车轮荷载。根据本文第3节提出的方法,以轮对无横向位移时为例,计算沿道岔转辙器线路纵向,轮轨法向力的转移和分配规律见图11。 由图11可知,轮对无横移时,标准车轮踏面条件下,轮载转移位置为距尖轨尖端6.24~6.68 m的范围,轮载转移段长度为440 mm;磨耗车轮踏面匹配时,其轮载转移位置为距尖轨尖端7.28~7.75 m的范围,轮载转移段长度为470 mm,相比标准车轮踏面,磨耗车轮踏面的轮载转移位置后移了约1 m的距离,根据参考文献[17]中给出的结论,在铁路道岔转辙器中,轮载转移的位置后移会导致轮对蛇形运动的距离和幅度出现较大程度的增大,并恶化轮轨横向动力相互作用。因此,磨耗车轮状态下的车辆进岔时,轮对蛇形运动的距离和幅度均会增大,降低车辆运行品质。 现场观察车辆在磨耗状态下进入道岔转辙器部件时,会出现轮对蛇形运动加大、轮轨动力相互作用增大等现象[1]。本文从轮轨接触点位置、两点接触范围、法向力的转移和分配三个方面对比分析了车轮磨耗前后不同轮对横移下轮轨接触的情况,并给出了相应的结论,车轮踏面的形状对道岔转辙器部件内轮轨两点接触的位置和特性有重要影响,分析结论与现场情况基本一致,从而验证了计算方法的合理性和可行性。 本文根据铁路道岔转辙器部件中尖轨与基本轨的空间位置关系以及轨下基础的布置方式,提出了考虑尖基轨相对运动的轮轨两点接触计算方法,并给出了两个接触斑处轮轨法向力的计算方法。以中国直向通过速度250 km/h的18号高速道岔转辙器为例,对比分析了标准和磨耗车轮踏面与尖基轨匹配时的接触状态,得到结论如下: (1) 车轮踏面的形状对道岔转辙器部件内轮轨两点接触的位置和特性有重要影响。 (2) 与标准车轮踏面相比,磨耗后车轮踏面与钢轨匹配时,其轮轨接触点位置多位于尖轨的轨距角附近,会增大尖轨的侧面磨耗。 (3) 磨耗后车轮踏面对应的轮载转移位置后移,车辆进岔时,会增大轮对蛇形运动的距离和幅度,从而恶化轮轨横向动力相互作用。 (4) 磨耗后车轮踏面与钢轨匹配时,其发生轮轨两点接触的可能区域较为分散,车辆轨道系统振动过程中,其轮轨接触状态容易在单点与两点接触之间切换,造成轮轨接触点的跳跃,从而引起较大的冲击振动作用。3 两点接触的法向力求解方法

4 转辙器部件静态轮轨接触几何关系
4.1 转辙器部件钢轨廓形

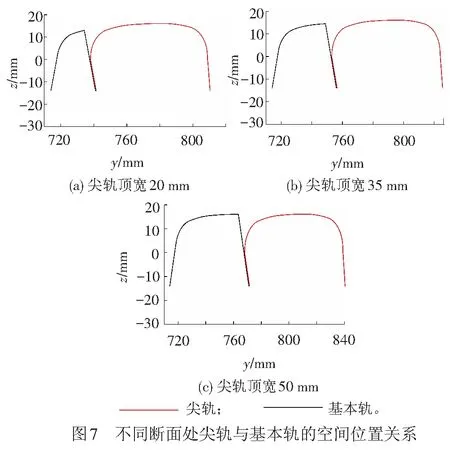
4.2 轮轨接触点位置分布

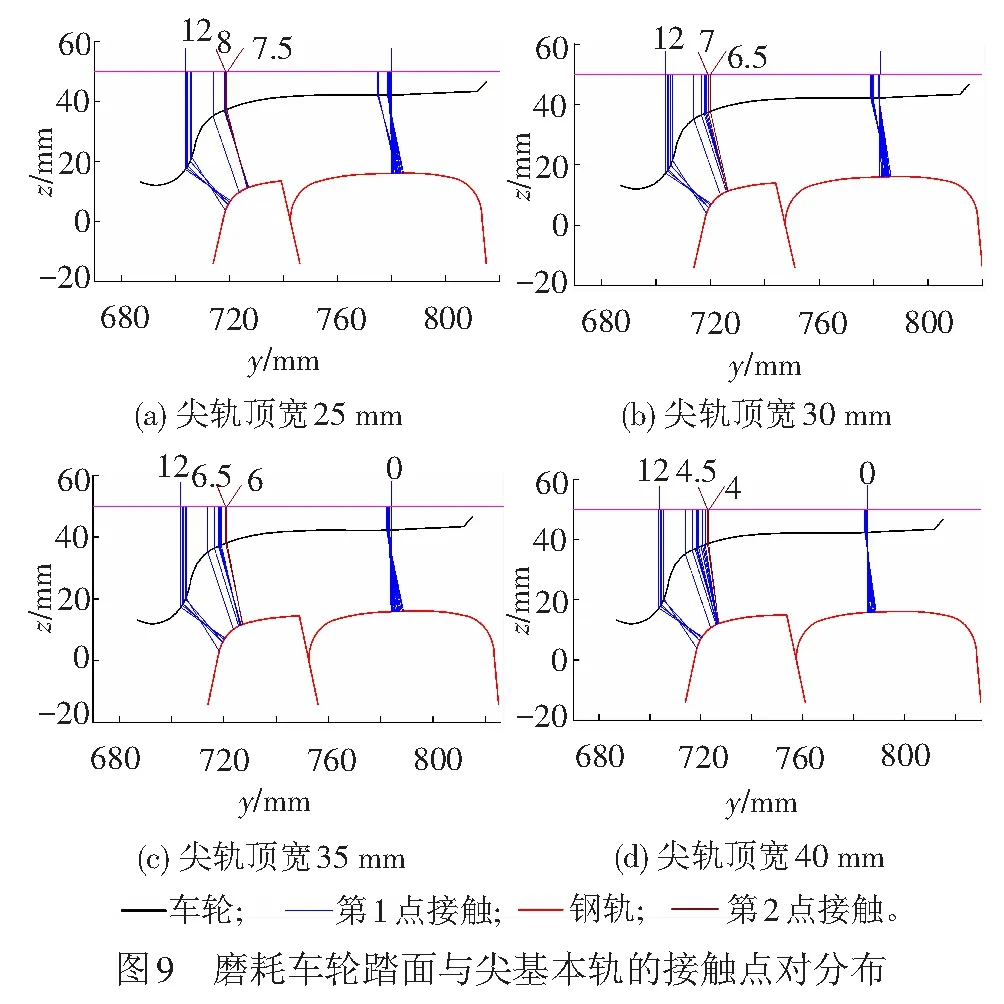
4.3 轮轨两点接触范围
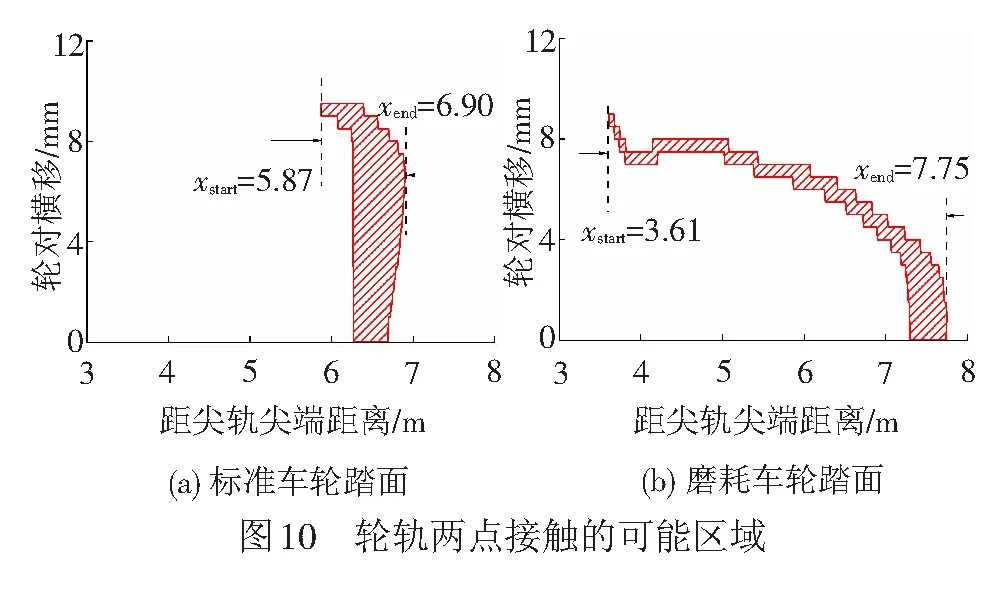
4.4 静态轮轨法向力转移和分配规律

5 结论
