列车运行速度对弓网电弧电气特性的影响研究

雷 栋， 张婷婷， 段绪伟， 高国强， 魏文赋， 吴广宁

(1． 中国铁道科学研究院 标准计量研究所， 北京 100081； 2. 西南交通大学 电气工程学院， 四川 成都 610031)

高速列车运行过程中，受电弓与接触网之间的接触方式会由于车体振动、轮轨不平顺、接触网硬点等因素由横向和纵向的滑动转变为垂向的振动和跳动，弓网的振动和跳动产生弓网离线，致使弓网电弧产生[1-2]。弓网电弧会产生高频振荡过电压对车载电器造成损伤，还会烧蚀受电弓滑板、接触网导线[3-5]，电弧烧蚀会影响滑板与接触网导线的服役寿命，烧蚀严重时甚至会导致接触网导线断裂，造成重大安全事故[6]。近年来，弓网电弧对滑板和接触线的烧蚀问题已经引起了国内外学者的广泛关注[7-9]。

早在1939年，在一定的假设条件下，基于能量守恒方程，Cassie[10]在国际大电网会议上提出可以从宏观角度研究电弧的外部电压和电流特性的电弧黑盒模型。1943年，Mayr[11]提出Mayr电弧模型方程。文献[12-13]分别使用Cassie和Mayr电弧模型，研究了高速列车弓网电弧的电压、电流特性。1958年，Browne[14]总结了Cassie和Mayr电弧模型不同的适用范围，认为在不同燃弧时刻，利用不同的电弧方程，电流过零前用Cassie模型，电流过零阶段用Mayr模型。Habedank[15]将Cassie和Mayr模型串联起来，弥补了Cassie和Mayr模型的缺点。基于Mayr模型中电弧耗散功率为常数的假设，一些研究者提出了改进的Mayr模型。文献[16]中考虑电弧电流对耗散功率的影响建立了改进的Mayr模型。文献[17]认为电弧耗散功率和时间常数取决于电弧电导提出了Schwarz模型。文献[18] 认为电弧时间常数为恒定值，耗散功率是输入功率的函数，提出了Schavemaker电弧模型，近些年来，许多研究者对Cassie和Mayr模型中假定的常数同时进行改进。文献[19]利用弓网电弧的实验数据对Cassie-Mayr串联电弧模型进行修正，仿真分析了列车过电压，描述了不同时刻的电弧特性。文献[20] 考虑了列车运行速度对弓网电弧电气特性的影响，改进了Habedank模型，该模型对电弧耗散功率和电压梯度进行修正，并讨论了弓网电弧动态特性与模型的参数关系。

Cassie和Mayr电弧模型都是基于开关电弧发展起来的，当给定时间常数、电弧电压梯度和能量耗散参数后，可利用电弧数学模型研究电弧电压、电流随时间的变化规律。然而传统的Cassie和Mayr电弧模型分别假设了电弧电压和耗散功率为恒定值，由此导致的局限性(Cassie电弧模型适用于大电流阶段，Mayr电弧模型适用于小电流阶段)使得以上2个模型仅从宏观角度进行了电弧电气特性的描述，而基于Cassie和Mayr模型改进的电弧模型对描述特定条件下弓网电弧电气特性具有一定的准确性。针对弓网离线电弧多影响因素的电弧模型依然处于较空白状态，因此，适用于高速列车弓网离线电弧数学模型的推导是很有必要性的。

针对高速列车运行环境的特殊性，本文首先采用数学模型的理论推导方法，考虑弓网离线电弧间隙、列车运行速度、电弧电流和温度对电弧耗散功率的影响，建立了优化的弓网离线电弧模型；其次，对改进的电弧模型通过试验和仿真进行了对比验证；最后，研究列车运行速度对弓网电弧电气特性的影响。

1 电弧模型改进

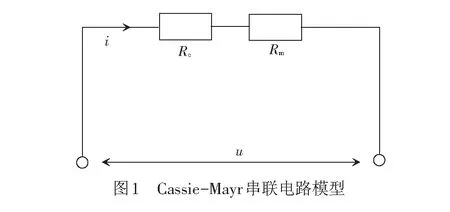
Cassie-Mayr串联电弧模型描述电弧的非线性特性，其电路见图1，Rc和Rm分别为描述Cassie模型和Mayr模型的电弧电阻。数学表达式为

( 1 )

式中：gm是由Mayr方程描述的电导；u是电弧电压；g是电弧电导；τm是Mayr方程时间常数；P0是单位体积电弧耗散功率常数；gc是由Cassie方程描述的电导；τc是Cassie方程时间常数；U是Cassie电弧电压梯度。

Cassie和Mayr模型的适用范围由于Cassie-Mayr串联电弧模型而得到扩展，在模型的建立和使用中，将电弧电压梯度U和电弧耗散功率P0设定为常数。然而Cassie-Mayr串联电弧模型在恒定U和P0的情况下仅能对电弧某一阶段的静态特性进行描述，不能反映电弧的动态变化特性，弓网电弧的电气特性得不到准确描述。

在实际的弓网电弧燃烧过程中，弓网电弧完全暴露在大气环境中，其电气特性主要受列车运行速度和弓网间隙的影响，此外还与电极结构、材料，回路电流、负载特性有关[19,21]。一方面，车顶气流场流速随着列车运行速度的提高而变大，对电弧的吹弧作用更加明显，将引起电弧耗散功率增大，冷却效果增强，同时导致弧柱弯曲变长，弧压上升；另一方面，更高的列车运行速度将导致更大的离线初速度，引起弓网平均离线间隙增大，弧柱被拉长，弧压增大[22-23]。上述影响因素将导致弓网电弧电压U和耗散功率P0不再是常数，而是受以上因素影响的变量。分析各因素对电弧的影响作用，对电弧电压梯度U和电弧耗散功率P0进行修正，使得改进的模型能准确地描述弓网电弧的电气特性。

电弧燃烧时，整个电弧可以分为3个区域、阴极区域、弧柱(电弧等离子体)和阳极区域。阴极区域和阳极区域在大气压下的空间尺度仅为10-4cm左右，电场强度很高。一般情况下，沿弧柱方向的电场强度近似为常数。因此，整个电弧压降可以表示为[24]

Uarc=Ua+Uc+Ul=ΔU+Ul

( 2 )

式中：Ua为阳极压降；Uc为阴极压降；Ul为弧柱压降；ΔU为阳极压降和阴极压降的和，其值主要与2个电极的材料、电极间气体和电弧电流有关。

大电流电弧稳定燃烧时，2电极的压降很小，可以忽略，电弧电压主要为中间弧柱部分压降Ul，其值仅与电弧长度成正比，经验值为15 V/cm。当间隙为l时，稳定燃弧电压可以表示为[20,25]

Ul=15×l

( 3 )

在稳定燃弧过程中，电弧输入的功率主要通过传导、辐射和对流3种方式散发到周围空气中。当列车高速运行时，弓网电弧受到强烈的气流吹弧，此时的主要散热方式为对流散热。横向吹弧和纵向吹弧是对流散热最常见的方式。横向吹弧是电弧轴向与气流运动方向垂直，可以认为对流散出的功率与弧柱纵断面面积成正比。纵向吹弧是气流运动方向与电弧轴向平行，可以认为由对流散出的功率与弧柱横断面面积成正比[26]。在列车运行中，由于弓网离线产生的电弧被拉长，使其长度远大于电弧直径，因此本文只考虑横向吹弧作用，即

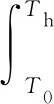
( 4 )

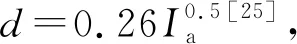
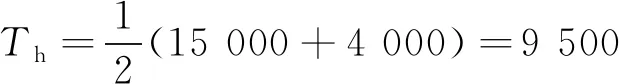
( 5 )

把式( 5 )带入式( 4 )可得

P0(v,l)=2.44×v×l

( 6 )

通过上述公式推导得到改进的电弧模型方程为

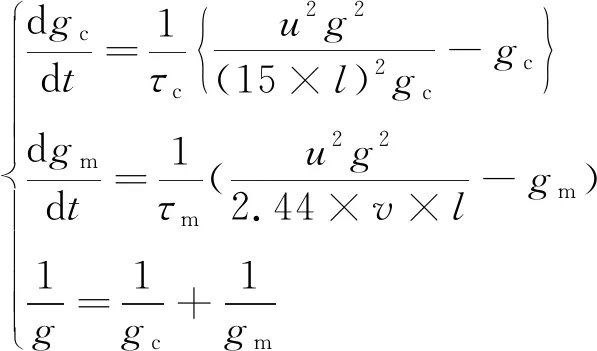
( 7 )

2 模型建立与验证

2.1 仿真模型建立

为了准确描述弓网电弧的电气特性，在仿真中采用实际牵引供电系统等效模型和参数。牵引供电系统等效电路模型见图2，其中US为牵引供电回路的等效电压源；RT为牵引变压器的等值电阻；RJ是接触网导线等值电阻；RC为电力机车等值电阻；LT为牵引变压器的等值电感；LJ为接触网导线等值电感；LC为电力机车等值电感；CJ为接触网导线对地等值电容。电弧的产生通过开关的通断来模拟。

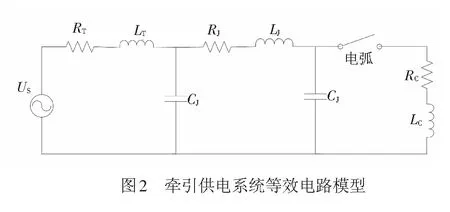
模型中电源电压值取牵引供电系统电压峰值35.35 kV，频率50 Hz。其他参数取值[22]见表1。

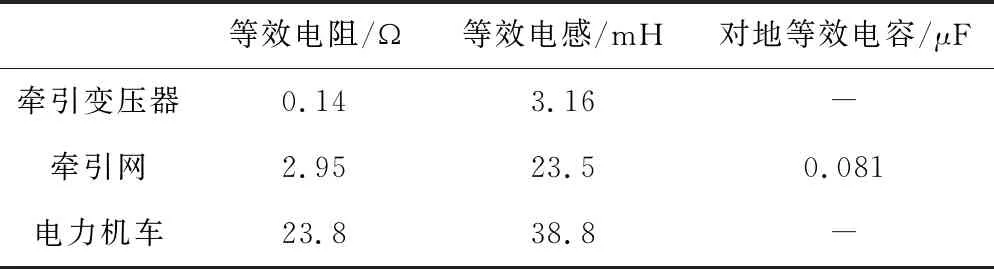
表1 牵引供电回路的等值电路参数

在改进的电弧模型中，确定出电弧时间常数、初始电导值、离线距离以及列车速度后，可以对其进行仿真计算。各个参数取值见表2。

表2 电弧仿真模型中的参数值

利用Matlab/Simulink库中的电力系统模块，根据弓网电弧数学方程式(7)建立弓网电弧模型，主要包括阶跃信号(Step)、重复信号(Repeating Sequence)、定值检测(Hit Crossing)、微分方程编辑器(DEE)、电压控制电流源(Controlled Current Sourse)元件。搭建的弓网电弧模型见图3。

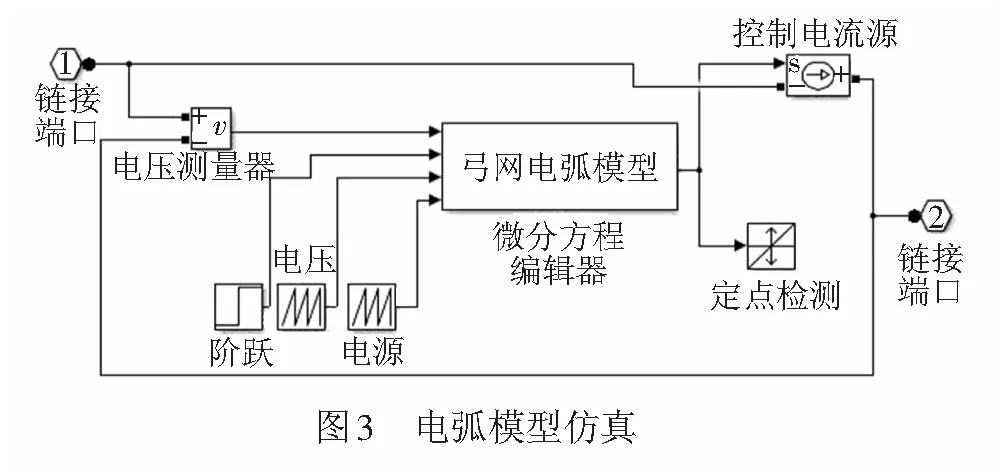
弓网电弧发生在弓网离线时，因此弓网电弧现象可以用断路器的开断近似模拟。在微分方程编辑器(DEE)模块中输入式( 7 )模拟弓网电弧外部特性，用式( 3 )、式( 6 )描述微分方程编辑器的4个输入量：电弧耗散功率P0，电弧电压梯度，电弧瞬时电压u(1)，阶跃信号u(2)。此外，将仿真模型看作电压控制电流源，使搭建的弓网电弧模型具有符合公式的电弧特性，其中，电弧电流的过零点的检测可通过定值检测模块完成；可控电流源元件既能控制微分方程编辑器的输出电流，又起到了模块的连接作用。

2.2 模型验证

采用电极分离放电产生电弧等离子体，通过外加风源模拟气流横向吹弧，验证改进的电弧模型的合理性和准确性。实验中电源电压为10 kV，频率50 Hz，电极间隙为6.5 mm，采用示波器记录电弧电压波形。

图4为实验测得的电弧电压波形。图5为仿真计算电弧电压波形改进前(式( 1 ))和改进后的电弧模型(式 ( 7 ))。在t时刻加入气流吹弧，从图4(a)、图5(a)中可以看出，在没有气流时，电弧电压波形比较稳定，电弧稳定燃烧，电极附近有收缩现象，电弧形貌近似呈圆柱形，采用改进前的电弧模型可以很好的描述该情况下的电弧特性。图4(b)、图5(b)有气流情况下，电弧被气流吹弯，并向外扩散，电弧电压波形中，与t时刻前的电弧电压相比较，有气流情况下，稳定燃弧电压略有增加，最大起弧电压明显增大，该情况下的电弧特性采用改进后的电弧模型描述则更为准确。不同的是，由于电极间隙变化引起的弧柱伸缩因素加入到改进的模型中，随离线时间增大仿真波形也呈现增大的趋势，实际弓网离线情况下变间隙的弓网电弧特性验证了该仿真的正确性。

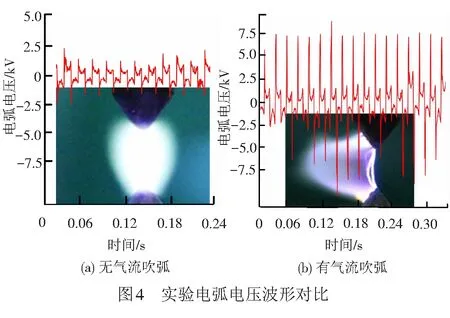
通过实验与仿真对比可以看出，改进的电弧模型能够准确地描述有气流情况下的电弧电气特性。同时也得到了气流对电弧参数特性的影响，即加入气流，电弧电压幅值增大。

3 仿真结果分析

本文使用Matlab/Simulink软件搭建模型，用该模型等效牵引供电系统，研究了列车运行速度为100、200、300、400 km/h情况下的弓网电弧电气特性。计算过程中，假定列车的等值电感LC和等值电阻RC保持不变。

3.1 弓网电弧电流特性

图6为不同速度下弓网电弧电流随离线时间变化的波形。不同列车运行速度下，电弧电流波形几乎重合。在第一个燃弧周期，电流峰值出现最大值，为1 080 A左右；0.01 s到0.1 s之间，正向电流峰值、负向电流峰值基本不变，为1 044 A左右。

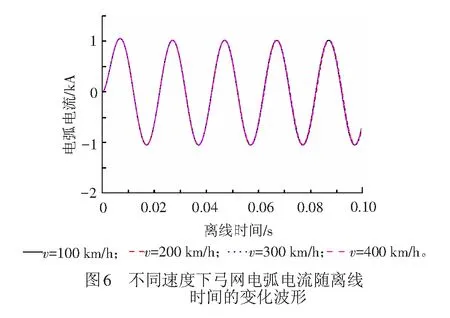
3.2 弓网电弧电压特性

图7为不同速度下弓网电弧电压随离线时间变化的波形。电弧起弧时，电弧电压迅速上升到最大值U1，即起弧电压，然后迅速下降到稳定燃弧电压U2，在半周期结束时，电弧电压又上升到熄弧电压U3。整体上，电弧电压波形明显偏离正弦波形，起弧电压U1、稳定燃弧电压U2、熄弧电压U3随着离线时间和列车速度的增大而增大。

为了更深入的研究在不同运行速度下，弓网离线时间对电弧电压的影响，分别提取每个燃弧周期内起弧电压U1、稳定燃弧电压U2随离线时间的变化情况，见图8。同样，提取不同燃弧周期内，起弧电压U1和稳定燃弧电压U2随运行速度的关系，对比图7中t1、t3和t2、t4时刻的起弧电压U1和稳定燃弧电压U2，见图9。

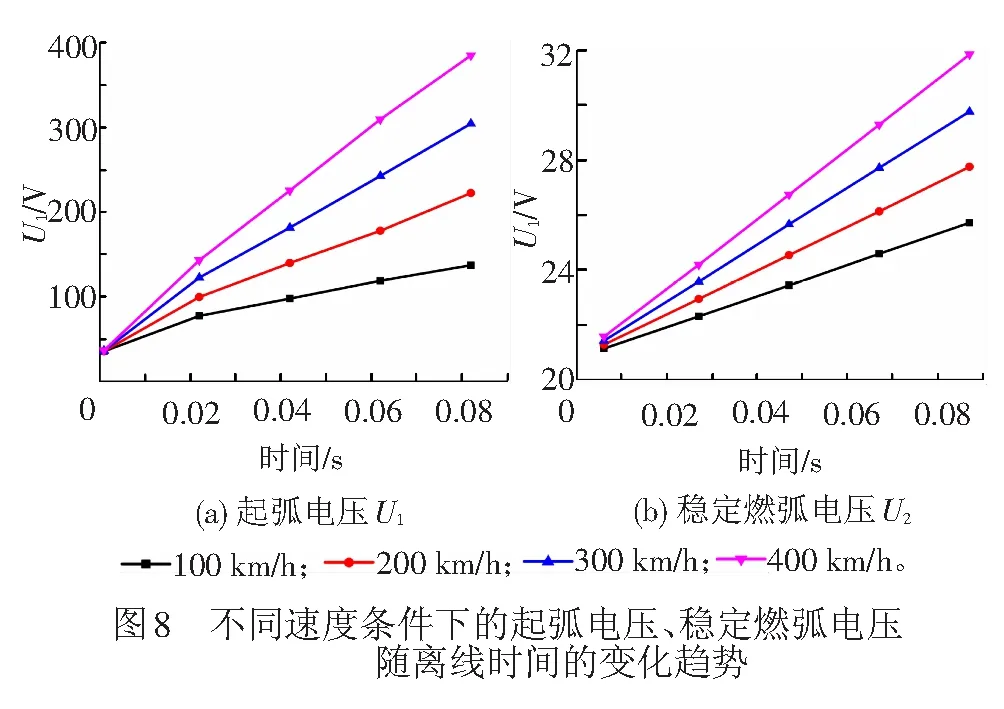
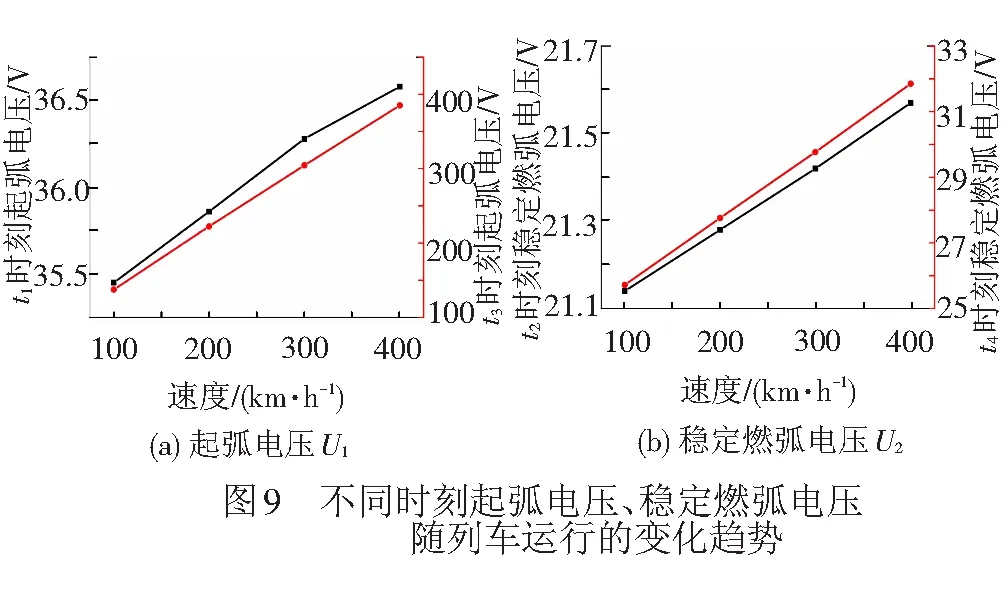
从图8(a)可以看出，同一速度下，弓网电弧起弧电压U1随离线时间的增大而增大。在0.02 s时，起弧电压U1出现转折，其中，列车速度为100 km/h的起弧电压曲线转折较明显。图9(a)具体显示了t1、t3时刻正向起弧电压U1随速度的变化趋势。速度分别为100、200、300、400 km/h情况下，t1时刻对应的起弧电压U1分别为35.45、35.86、36.28、36.58 V，电压变化较小；t3时刻不同速度下对应的起弧电压U1分别为137.34、222.43、304.5、385.16 V，电压变化明显，速度每增加100 km/h，起弧电压增加约81～85 V。可见，离线时间越长，速度对起弧电压的影响越明显。

图8(b)表明，稳定燃弧电压U2随离线时间呈现增大趋势，速度越大，增幅越大。在不同时刻，速度对稳定燃弧电压U2的影响见图9(b)，速度分别为100、200、300、400 km/h的情况下，t2时刻对应的的稳定燃弧电压U2为：21.14、21.28、21.42、21.57 V，变化幅度较小，速度每增加100 km/h，电压增加约为0.14 V，对应的电弧功率增加约为146 W。t4时刻不同速度对应的稳定燃弧电压U2分别为：25.72、27.76、29.77、31.85 V，速度每增加100 km/h，电弧电压增加约为2.05 V，电弧功率约增加2 140 W。可见，离线时间越长，电弧越长，电弧功率越大，速度对稳定燃弧电压的影响越大。

综上可得，燃弧0～100 ms内，列车运行速度从100 km/h增大到200 km/h时，弓网电弧起弧电压范围为35～386 V，稳定燃弧电压范围在20～30 V之间。对比文献[19，22，27-28]中分别通过仿真和实验得出的数据：弓网电弧起弧电压范围为35～400 V，稳定燃弧电压范围为5～40 V，其中以20 V左右为主。可以看出，本文仿真得出的数据与上述文献研究得出的数据一致。

由式( 6 )可知，弓网电弧对流耗散功率与列车速度和电弧长度的乘积成正比，所以对于同一离线时间，电弧耗散功率与列车速度成正比，当速度增大时，对流耗散功率增大，电弧的冷却效果变强，在电弧未熄灭之前，需要提供更多的输入能量维持电弧的燃烧，因此，电弧电压增大。同样，在同一列车速度下，电弧对流耗散功率与电弧长度成正比，当弓网离线时间增大，电弧被拉长，一方面电弧弧柱的电压随着电弧的拉长而增大，电弧电阻也随之增大；另一方面，对流耗散功率增大，电弧冷却效果增强。

3.3 弓网电弧伏安特性

为了研究列车运行速度对弓网电弧电阻的影响，图10给出一个周期(0.042 ～0.062 s)内，弓网电弧的伏安特性曲线。其中，图10 (a)、图10 (b)分别为列车运行速度为100、400 km/h的伏安特性曲线以及对应的局部放大图A、B。

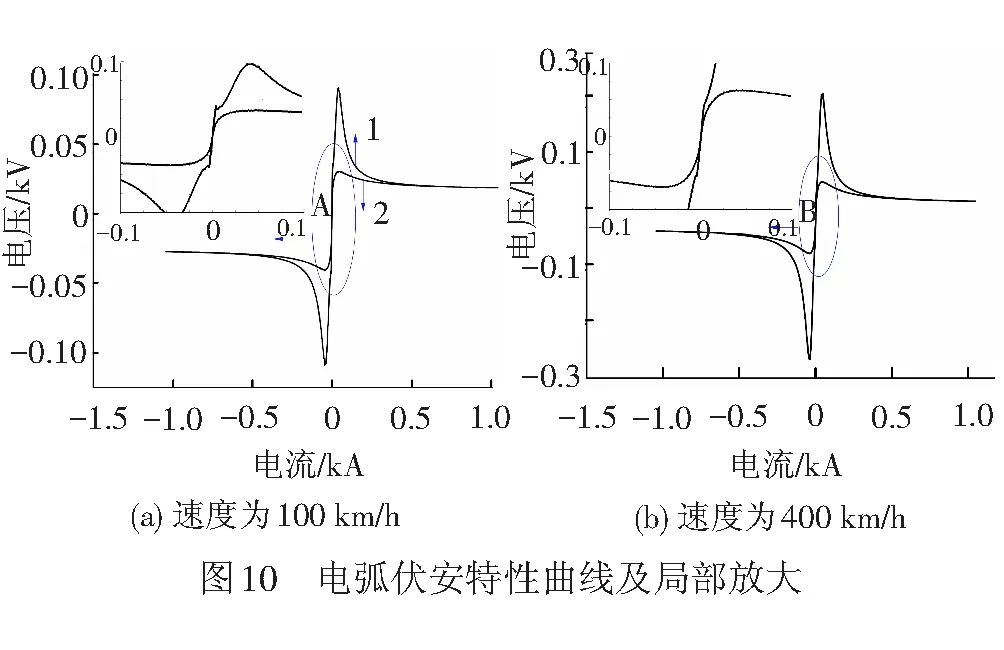
从图10可看出，弓网电弧电压电流之间呈现高度非线性关系，电弧电阻等于电弧电压瞬时值和电弧电流瞬时值的比值。弓网离线时，电弧电压达到弓网间隙气体击穿电压，弓网电弧产生，电弧电阻迅速下降，电流开始增加，当电弧电流达到最大值之后，电弧电阻缓慢上升，电流下降。当电流即将过零时，电弧电阻迅速上升，此时若弓网间隙空气介质恢复强度小于弧隙上的电压恢复强度，则电弧重燃。在此过程中，电弧伏安特性曲线由2条曲线构成，图10(a)的曲线1和2。曲线1反映了电弧电流增大时的特性，曲线2反映了电弧电流减小时的特性，曲线2在曲线1下方的原因是由于电极和弧柱气体的热惯性，使弓网电弧伏安特性曲线近似磁滞回线，一个周期内稳定燃弧阶段斜率为负。

对比图10(a)、图10(b)，速度为100 km/h和400 km/h的伏安特性曲线都近似为磁滞回线，但400 km/h的电弧电压幅值大。电弧电流最大时，运行速度为100 km/h的电弧电阻为22.5 mΩ，运行速度为400 km/h的电弧电阻为25.8 mΩ，速度增大，电弧电阻增大。为比较电弧过零阶段，速度对电弧电阻的影响，对电流过零区域A、B的伏安特性进行放大，在电压为-50～50 V的范围内，速度越大，曲线的斜率(电弧电阻)越大，速度为400 km/h时，该范围内的电压不对称。可见，列车运行速度增大，电弧电阻也会增大。

4 结论

本文考虑了列车运行速度和电弧长度，改进了串联的Cassie-Mayr电弧模型，通过试验和仿真对比验证了模型的合理性，研究了速度对弓网电弧电气特性的影响，得到以下结论：

(1) 弓网起弧电压随着列车运行速度、弓网离线时间的增大而增大。当燃弧时间0～100 ms内、运行速度为100 km/h时，弓网起弧电压幅值从35 V增大到137 V；速度增大为400 km/h，起弧电压从37 V增大到 386 V。运行速度越大，离线时间对弓网起弧电压影响越大。

(2) 弓网稳定燃弧电压随着列车运行速度、弓网离线时间的增大而增大。列车运行速度从100 km/h增加到400 km/h，初始时刻t2的稳定燃弧电压在21～22 V之间，t4时刻(87 ms时)的稳定燃弧电压在25～32 V之间；速度每增加100 km/h，t2时刻的稳定燃弧电压增加约为0.14 V，对应的电弧功率约增加146 W；t4时刻的稳定燃弧电压增加约为2.05 V，电弧功率约增加2 140 W。离线时间越长，电弧电压越大，电弧功率增加量越大，速度对稳定燃弧电压的影响越大。

(3) 列车运行速度增大，电弧电阻也会增大。电流峰值时，速度从100 km/h增加至400 km/h时，电弧电阻由22.5 mΩ上升到25.8 mΩ。