地铁列车曲线运行振动源强特性分析

刘维宁， 杜林林,2， 刘卫丰

(1. 北京交通大学 土木建筑工程学院， 北京 100044； 2. 中国中元国际工程有限公司 技术研究院， 北京 100089)

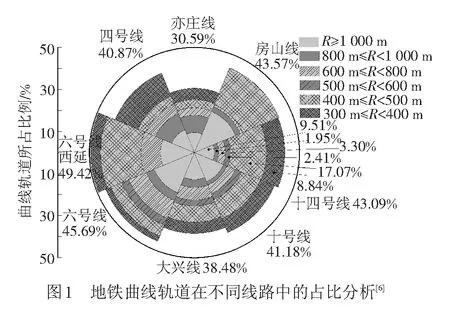
近些年来，随着城市轨道交通路网的逐步加密，列车行驶产生的环境振动提升了城区环境振动水平，这对线路周边居民的正常生活，对建筑物的结构安全及精密仪器的工作[1-2]造成了不利影响。其中，由于列车曲线运行环境振动影响的预测评估并未真实考虑列车曲线行驶的垂-横向动力耦合作用，未能真实的反应实际行车速度不满足设计超高所需要行车速度的情况，因此曲线地段环境振动影响超标现象更为突出[3-5]。经统计，地铁曲线轨道占线路总长度的比值高达30%～50%，见图1[6]。到目前为止，对于地铁曲线轨道来说，列车行驶引起的振动源强特性、振动传播规律等问题仍不十分清楚。

与直线轨道不同的是，列车通过曲线轨道时，列车-轨道动力相互作用具有显著的垂-横向动力耦合特性。由此引发许多轨道及车辆行业内特别关注的问题，如钢轨波浪形磨耗现象[7-8]。当列车通过曲线轨道时，并不能完全满足线路设计超高所需要的行车速度，由此产生的轮轨附加动力作用，除了对轨道及车辆运行带来影响之外，其特殊的振动源强特性产生了与直线运行不同的环境振动影响。根据现场测试发现，列车以同样速度通过直线轨道时产生的环境振动小于曲线轨道[9]，且列车行驶于曲线轨道时，地表的水平向振动强度大于竖向的情况时有发生[4,10-11]。对此，以往计算与评估未做出严谨的考虑，因而带来了较大的列车振动环境影响评估误差。作为轨道交通环境振动与二次噪声评估的一个重要的基本因素，地铁列车在曲线上运行所产生的振动源强，至今为止仍未进行系统深入的研究。现有的针对曲线轨道轮轨动力相互作用研究的主要方向是在轮轨接触状态、轮轨界面粗糙度等随机因素对轮轨磨耗、车辆运行安全性、舒适性等方面的影响[12-13]。而环境影响的研究仍不够充分，当曲线轨道占比达到50%时，对列车振动环境影响评估的准确性产生了不容忽视的效果。

目前，对列车运行诱发区域环境振动的预测及评估工作，在行业规范中是基于链式衰减的经验预测法，在曲线地段，规范仅采用一个常数修正值对曲线地段进行经验性修正，并未考虑曲线轨道上车-轨动态垂-横向相互耦合作用。在采用数值法对包括轨道-隧道-地层一体性模型进行动力分析时，也仅考虑垂向振源激励[14]，预测结果与实测相比有较大差距。当考虑列车曲线通过时的横向作用时，研究发现可提高曲线轨道振动预测的准确性[15]。另一方面，地铁沿线附近的某些特殊振动敏感目标，对水平向的振动会要求更加苛刻，有时这种要求会达到10-1～10-3mm量级[16]。除此之外，在地铁曲线地段，当采用降速措施控制环境振动影响时，有时降速运行不仅不能缓解振动超标问题，反而增加了振动影响。

综上所述，为了提高地铁环境振动影响预测的精度与准确性，必须重视线路曲线段预测的精度与准确性。而这就要求首先必须解决列车曲线轨道运行时的振动源强特性问题，研究车-轨关键参数与振动源强的因果关系问题。

振动源强是指在对列车运行引起的周围环境进行振动及噪声影响分析时，输入到预测评估模型中的振动物理量，通常包括轨道振动加速度级或振动荷载、振动加速度。对振动源强特性进行研究，经常采用的方法是试验分析法和模型分析法。采用模型分析法研究曲线轨道-车辆动力相互作用时，目前主要围绕着列车曲线行驶时列车和轨道结构的安全性、轮轨动力匹配以及轮轨接触磨耗等方面进行[12,17]。鲜有关注车辆曲线运行时车辆-轨道间垂-横向动力耦合作用对环境影响分析的研究。比如，当采用解析法研究车轨耦合作用时，轨道模型通常采用直梁近似模拟曲线钢轨[18]，而不考虑曲率半径对模型计算精度的影响。若采用连续支承曲梁模拟曲线轨道，同时考虑曲率半径影响时，却忽略了离散支承的作用[19]。如采用时域法对车-轨动力耦合模型进行分析，通常取有限长轨道结构进行计算，而这样仅能得到近似解，大量反复的数值计算无法反应车-轨关键参数与振动源强的因果关系。综上可知，研究列车曲线轨道运行时的振动源强特性问题，弄清曲线行车时车-轨关键参数与振动源强的因果关系，需要寻找一个理论可靠、计算高效的办法。

为此，本文通过建立离散点支承曲线轨道动力学模型，进而在频域内，采用解析函数的方法，实现了曲线轨道-列车空间解析耦合，从曲线轨道车轨耦合基本力学机理上，对曲线轨道振动源强特征开展了系统性的研究。

1 车-轨空间耦合模型

1.1 曲线轨道结构动力学模型

本文结合曲线轨道的结构特点，采用等间距离散点支承曲线梁力学模型对其进行模拟，用曲线Timoshenko梁模拟曲线轨道钢轨的力学性质，用弹簧-阻尼模型模拟支承系统的刚度及阻尼特性，由此建立了曲线轨道结构动力学模型，见图2。图2中，Fx、Fy分别为移动速度为v的横向、垂向外荷载；Tz为移动速度为v扭转荷载。

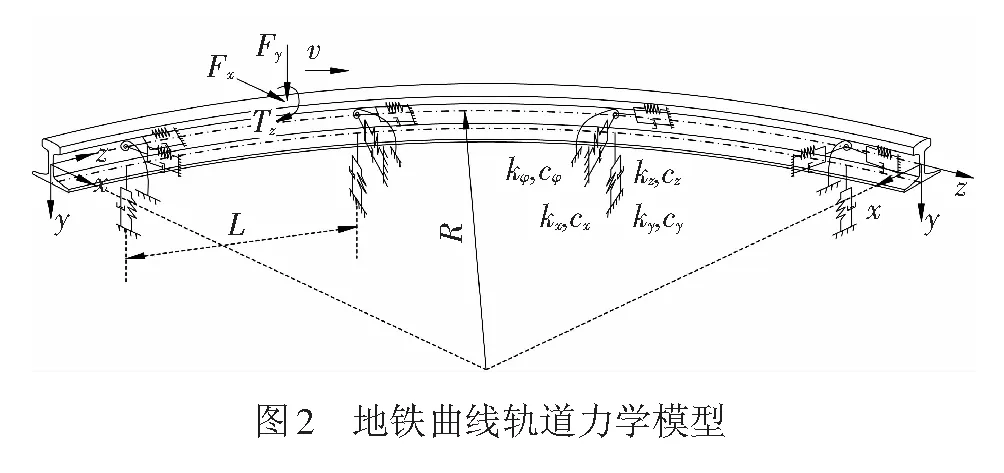
结合曲线Timoshenko梁静力学平衡方程[20-22]，以及曲线轨道结构的受力特点，可得曲线轨道结构动力学控制方程

( 1 )

( 2 )

( 3 )

( 4 )

( 5 )

( 6 )

本文将任意长度的曲线轨梁，视为具有相同曲率半径并存在某种数学周期的、虚拟的圆形环结构的一部分，该结构的数学周期可取为扣件支点间距L。由此，根据无限周期性结构理论[23]及曲线轨道梁动力响应的频域数学模态叠加法[24-25]，对上述方程进行求解，可得到地铁曲线轨道结构的动力响应频域解。

1.2 车辆模型

本文将地铁车辆简化为多刚体系统，车体、2个构架以及4个轮对同时考虑横移、沉浮、侧滚等自由度，除此之外车体和构架还考虑了点头、摇头自由度。一系、二系悬挂采用弹簧阻尼单元模拟。其中曲线轨道-车辆相互作用力学简化模型见图3。

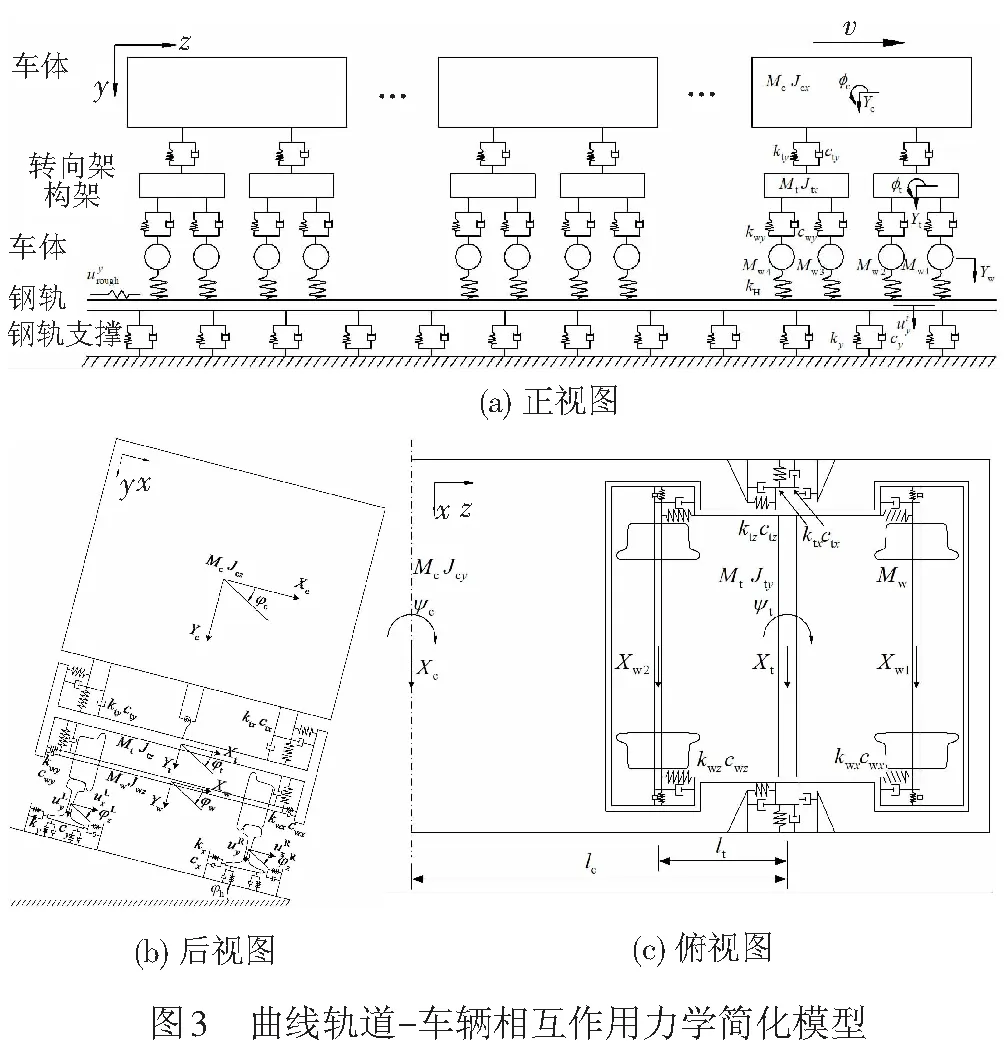
由达朗贝尔原理可知车辆运动方程为

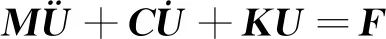
( 7 )

1.3 轮轨耦合关系及轨道不平顺

将轨道不平顺视为弱平稳Gauss随机过程，具有近似各态历经的特点，其样本可通过三角级数叠加法得到[26]。

由于轮轨耦合关系受轨道系统、车辆系统、轮轨接触状态等因素的影响，本文在对城市轨道交通振动源强特性的分析中，将影响轮轨动力相互作用的因素分为以下2个部分：

(1) 定常因素。即轨道结构(含标准扣件、减振扣件、减振轨枕、浮置道床等)，轨枕离散支承，行车车速，加减速运行，曲线半径及超高等。

(2) 随机因素。即轮轨接触状态，轮轨界面粗糙度，轨道不平顺谱，钢轨波浪形磨损，焊接接头，养护维修状态等。

作为阶段性成果，本文在建立轮轨耦合关系时，基于线性相互作用假定，主要考虑了列车稳态曲线通过时的振动源强特性问题，即主要研究了“定常因素”对曲线轨道振源特性的影响。

考虑到地铁环境振动源强特性的主要关心频率为1～100 Hz[27-28]，假设轮轨接触点位于钢轨轨头中心线上，视轮轨动力相互作用为线性作用，并将轮轨力分解为垂向荷载以及横向蠕滑荷载。

根据Hertz接触理论，车轮与钢轨之间的垂向耦合满足如下方程[8](以列车第k轴左侧轮轨垂向耦合关系为例)

( 8 )

轮轨蠕滑荷载[29]可由Kalker线性蠕滑理论计算得到(以左侧轮轨关系为例)

( 9 )

对于轮轨耦合关系，为满足本文的轮轨线性相互作用假设，在求解蠕滑荷载时各蠕滑系数需为常数，即，轮轨间垂向力为静轮轨力，锥形踏面车轮是锥度为0.05的圆锥面，接触点钢轨横断面外形为0.3 m的圆柱体[30-31]，为简化计算，不考虑曲线轨道-车轮相互作用时，横向蠕滑与车轮旋转二者之间的影响[32]。此时的轮轨接触关系为轮轨跟随模式，在此基础上，对轮轨间的横向蠕滑力进行求解。

频域内轮轨间横向蠕滑力[30-31](以列车第k轴左侧轮轨横向耦合关系为例)为

(10)

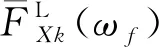
同理，可以求出曲线轨道-车辆的右侧垂/横向轮轨力。

1.4 动态轮轨力求解

根据上述轮轨空间耦合关系，可求得动态轮轨力

(11)

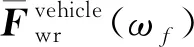
通过求解方程(11)，并对不同角频率ωf时的方程进行求解，即可得频域内的轮轨力。

以上讨论给出了曲线轨道的空间模型、车辆模型、曲线轮轨耦合空间关系以及频域求解思路。通过对比轨道模型中的柔度系数、车辆蛇形运动规律以及与实测案例的对照分析，在作者的另一篇论文中证明了上述曲线轨道车轨空间耦合解析模型的正确性[6]，这里不再赘述。

2 曲线轨道振动源强支反力特性研究

与直线轨道结构相比，曲线轨道结构的特殊之处在于曲线半径以及为了平衡车辆离心力而设置的曲线超高。当根据运营需要，车辆运行速度提高或降低时，列车曲线行驶状态将发生改变。这时行车速度、曲线半径及曲线超高三者之间存在未被平衡的超高作用。在进行列车振动环境影响评价时，这一作用将对曲线轨道行车时的振动源强产生重要影响。

为了考察曲线轨道行车振动源强的特性，如幅值、方向以及频率分布等，本文对行车速度、曲线半径、超高等因素进行了综合分析，研究未被平衡超高的差值对曲线轨道振动源强的影响。与此同时，本文计算了同样行车条件下的直线轨道的振动源强特性，以供对比参考。

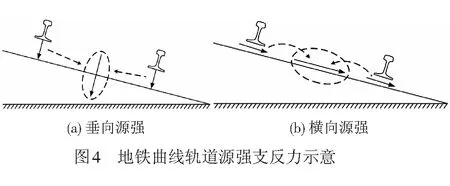
为了简洁表示曲线轨道的振动源强特点，本文提出源强支反力的概念。源强支反力表示曲线轨道的轨下基础动力荷载沿道床垂向及横向的合力[30]，见图4。

2.1 主要计算参数

计算模型中各因素参数取值说明如下。

(1) 曲线半径

根据图1中地铁线路曲线半径的分布特点，并结合GB 50157—2013《地铁设计规范》[33](简称《规范》)，本文计算半径为500、700 、1 000、2 000 m。

(2) 行驶速度

根据《规范》[33]中对运营规模的一般要求，本文取列车行驶速度为40、60、80 km/h。

(3) 未被平衡超高值

未被平衡超高值，表征车辆所处的欠/过超高状态，下文将其简称为“欠/过超高值”。根据《规范》中的地铁曲线轨道对欠/过超高值的设计范围，本文计算选用欠/过超高值为60、30、0、-30、-60 mm。

由于本文主要考察振动源强随各因素变化的一般性规律，因而并未严格按照实际需要限定超高的设置值，对于部分参数不符合设计要求的计算情况，仅作为规律性研究使用。

以上分析参数见表1。

计算分析时的车辆、轨道参数本文参考了文献[6]，计算中考虑了轨道不平顺。不平顺谱采用美国五级不平顺谱。

在对源强支反力进行分析时，主要评价指标如下：

(1) 时域有效值(RMS)

时域有效值又称均方根值(root-mean-square value，RMS)，可以表征源强支反力的强度。

(2)三分之一倍频程(1/3 OB)

三分之一倍频程(1/3 octave band，1/3 OB)，可以反映源强支反力在不同频段上的分布情况。

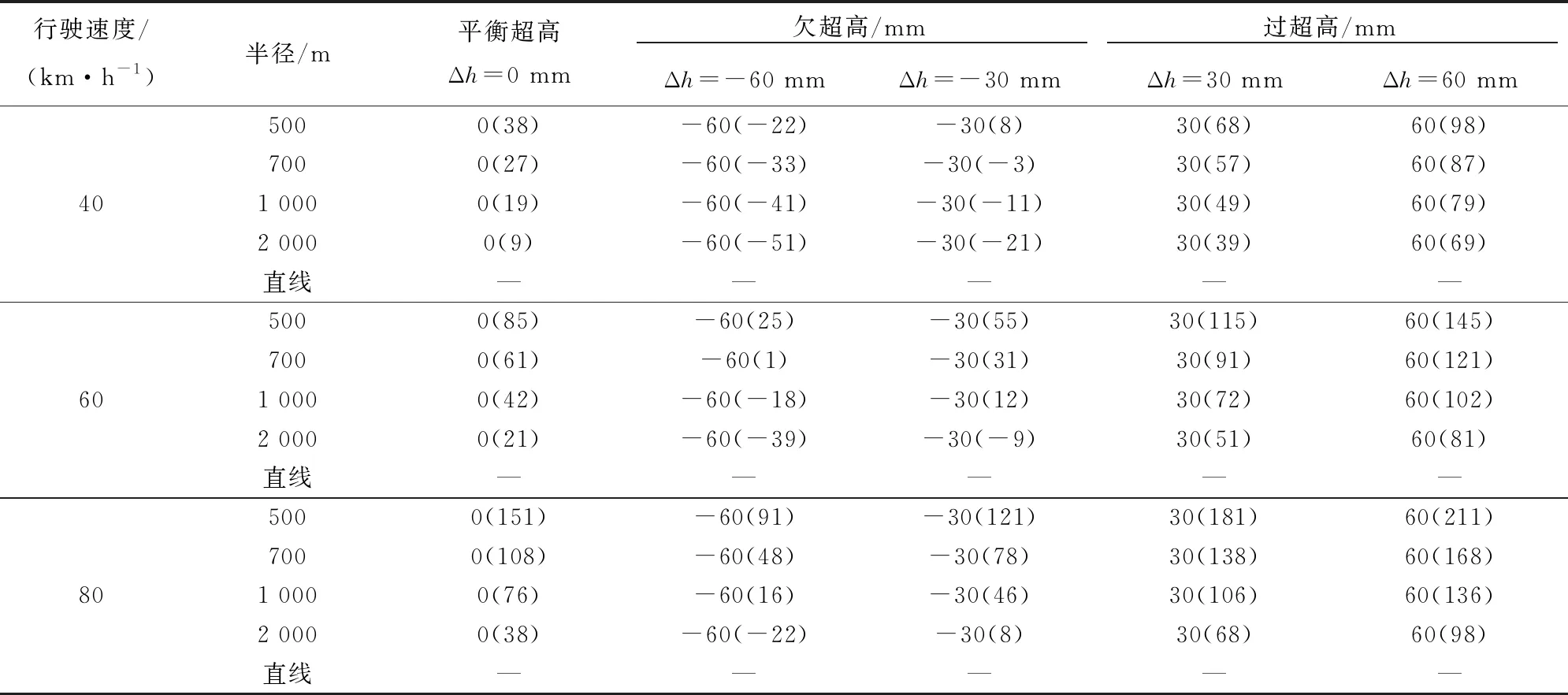
表1 曲线轨道振动源强分析参数

注：括号内为实设超高值。

2.2 曲线轨道源强支反力有效值分析

当曲线半径、列车行驶速度变化时，欠/过超高值对曲线轨道源强支反力有效值的影响关系见图5。

由图5可知：

(1) 地铁曲线轨道垂向、横向源强支反力有效值与欠/过超高值呈线性关系；垂向、横向源强支反力有效值在平衡超高点处最小，但都大于直线轨道。

(2) 列车以相同的轴重、速度通过地铁曲线轨道和直线轨道时，地铁曲线轨道结构源强支反力将大于直线轨道结构。

(3) 平衡超高点处，曲线轨道振动源强与直线轨道较为接近，当曲线轨道欠/过超高值增加时，地铁曲线轨道与直线轨道的差异显著增大，在允许的最大欠/过超高值条件下，地铁曲线轨道垂向源强支反力有效值最大为直线轨道的1.09倍，横向源强支反力最大为直线轨道的5.4倍。

2.3 曲线轨道源强支反力频域分析

本文对曲线轨道源强支反力的频域分析，采用三分之一倍频程表示，得到图6、图7所示的变化曲线。

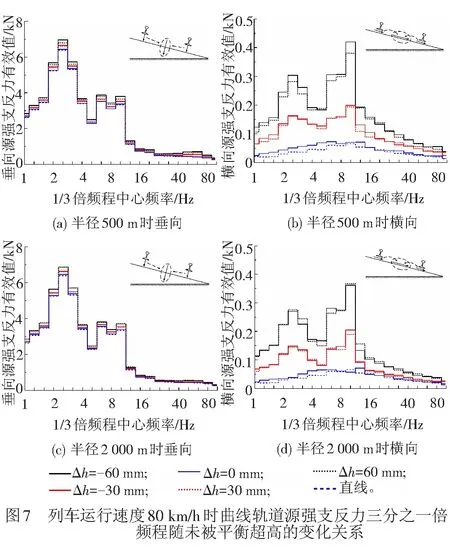
由图6、图7可知：

(1) 当行车速度相同时，不同欠/过超高值对垂向源强支反力频率分布基本没有影响，对横向源强支反力频率分布具有显著影响。

(2) 平衡状态时，各频段横向源强支反力响应幅值最小，随着欠/过超高值的增加，各频段响应幅值有所增大。

(3) 源强支反力在垂向和横向2个方向上，其频率分布均呈现为鞍型分布，且该分布存在2个并不对称的峰值频段；在各频段内，列车行驶速度对源强支反力强度及其分布具有明显的影响；频率分布中的峰值响应与列车轴荷载作用以及列车的蛇形运动有关。

(4) 曲线轨道横向源强支反力频率分布形状，在平衡超高点处呈山型，列车行驶速度对各频段的量值变化影响明显。

3 结论

城市轨道交通线路中曲线轨道占比高，其相应的环境振动影响与直线情况有显著不同，为了探讨其机理，本文通过建立离散点支承曲线轨道动力学模型，进而在频域内，采用解析函数的方法，建立了曲线轨道-列车空间解析耦合模型，从曲线轨道车轨耦合基本力学机理上，对曲线轨道振动源强特征开展了系统性的研究。该模型力学概念清晰，除必要的假设外，不存在计算误差，计算效率高。基于该理论模型，本文通过参数分析，得到了地铁列车曲线轨道运行时，振动源强的源强支反力在大小、频率分布上的变化特性。主要结论如下：

(1) 地铁列车在曲线轨道运行时，垂向源强支反力远大于横向；垂向、横向源强支反力与轨道的欠/过超高值呈线性关系，且都大于直线轨道情况。

(2) 曲线轨道源强支反力的频域分布呈非对称鞍型分布；其垂向作用分布受行车速度影响显著，而横向作用受列车行驶速度、曲线半径和超高的影响显著。

(3) 在对列车振动环境影响进行评估时，现有规范所采用的经验性修正方法，忽略了地铁曲线轨道行车的轮轨的空间动力垂-横向耦合作用，过低的估计地铁曲线轨道源强，因而可靠性很低。

(4) 在对曲线地段的列车振动环境影响超标现象进行整治时，不可简单采取降低运行速度的措施，因为只有在平衡超高速度运行时，才能使列车振动源强最小，否则都将使得振动源强不降反增。