基于改进双Sigmoid模型的磁流变减振器力学建模研究

彭 虎， 张进秋， 刘义乐， 张 建， 彭志召， 孙宜权

(1.陆军装甲兵学院 装备保障与再制造系,北京 100072； 2.陆军装甲兵学院 车辆工程系,北京 100072)

磁流变减振器(Magneto-Rheological Damper, MRD)是一种结构简单、阻尼可调性好且易于控制的智能半主动控制执行器，通过改变阻尼活塞上绕制的线圈内电流的大小，改变活塞与钢筒间隙内的磁场强度，从而改变间隙内磁流变液的黏度，实现阻尼可调。MRD具有响应快、设计灵活性好、阻尼力大、可靠性好、能耗低且成本低等优点，广泛应用于建筑、桥梁、汽车及列车等工程领域[1-3]。为了实现对MRD的有效控制，需要建立其力学模型。由于黏滞阻尼力的存在，MRD的力学特性曲线存在一定的滞回特性，给建模带来困难[4]。

国内外学者对MRD力学模型的建立展开了广泛研究，由于MRD的变阻尼过程涵盖了电、液、磁、固等多方面领域的内容，且其力学模型存在非线性特性，应用流变学理论推导其力学模型非常困难，因此，通常在建模时基于试验数据来展开。目前，典型的MRD力学模型可以分为参数化模型和非参数化模型两类，相比于利用神经网络等智能算法建立的非参数化模型，参数化模型可描述MRD阻尼特性曲线的阻尼、刚度、形状及力学特性等问题，具有意义明确，易于建模及工程实现等优点[5]。Stanway等[6]提出了Bingham模型，其表达式简洁，各参数意义明确，但Bingham不能准确表示高速条件下阻尼力衰减情况，以及低速下的阻尼力-速度曲线滞回特性，精度有限。Gamoto等[7]针对MRD阻尼力偏置及存在黏塑性现象等问题，提出了Bingham黏弹塑性模型，建模时添加摩擦力及弹性力，有效解决了阻尼力偏置及黏塑性问题。Werelwy等[8]根据Bingham模型无法描述低速下阻尼力-速度曲线的滞回特性问题，提出了非线性双粘力学模型，将屈服前区和屈服后区分别建模，可较好的描述滞回特性问题。但该模型采用分段函数表示，函数不连续，且依旧无法表示阻尼力衰减现象。陈凡[9]提出了一种可描述滞回现象及阻尼力衰减现象的参数化滞回模型，但该模型在速度提高或者电流加大之后，曲线形状与滞回曲线差异较大，无法满足建模需求。Wen[10]提出的Bouc-wen模型可有效描述低速下的滞回特性，与MRD试验曲线的拟合度较高，但需要14个拟合参数，且表达式中存在微分方程，模型较复杂，且其部分参数意义并不明确。徐赵东等[11]根据MRD阻尼力与速度的非线性特性与Sigmoid函数表达式类似的现象，提出了阻尼力Sigmoid模型，但该模型无法描述滞回现象。李秀领等[12]根据MRD滞回曲线中上下两分支形状的对称特性，利用双sigmoid函数来构建MRD力学模型，但该模型并未考虑位移与阻尼力的关系，蓄能器刚度特性的影响，以及阻尼力偏置因素。

本文基于MRD性能试验数据，考虑电流、位移、速度对MRD阻尼力建模的影响，提出一种改进型双sigmoid模型(Improved Double Sigmoid Model, IDSM)，对其参数的含义及对模型的影响进行分析，探讨各参数与电流及速度的关系，并对参数进行辨识。最后，采用误差均方根值，对模型输出阻尼力及试验得到的阻尼力值的差异性进行分析，验证模型的准确性。

1 MRD性能试验

1.1 MRD设计

设计的筒式MRD主要由供电线、活塞、活塞杆、线圈、浮动活塞、补偿气室及钢筒等部分组成，其结构如图1所示。活塞由内阻尼活塞和外导向活塞组成，可缩短轴向尺寸，磁回路从导向活塞绕回，可减小漏磁。导向活塞上下端开有MRF流通孔，阻尼缝隙采用环形缝隙式结构，MRF工作模式为阀式。活塞在拉伸和压缩过程中，活塞两端产生压差，MRF在压差作用下流过阻尼缝隙。此时，若给线圈加电，产生的磁场垂直于阻尼缝隙，从而改变缝隙内MRF的黏度，改变阻尼力，实现变阻尼，通过改变电流的大小可实现阻尼连续可调。

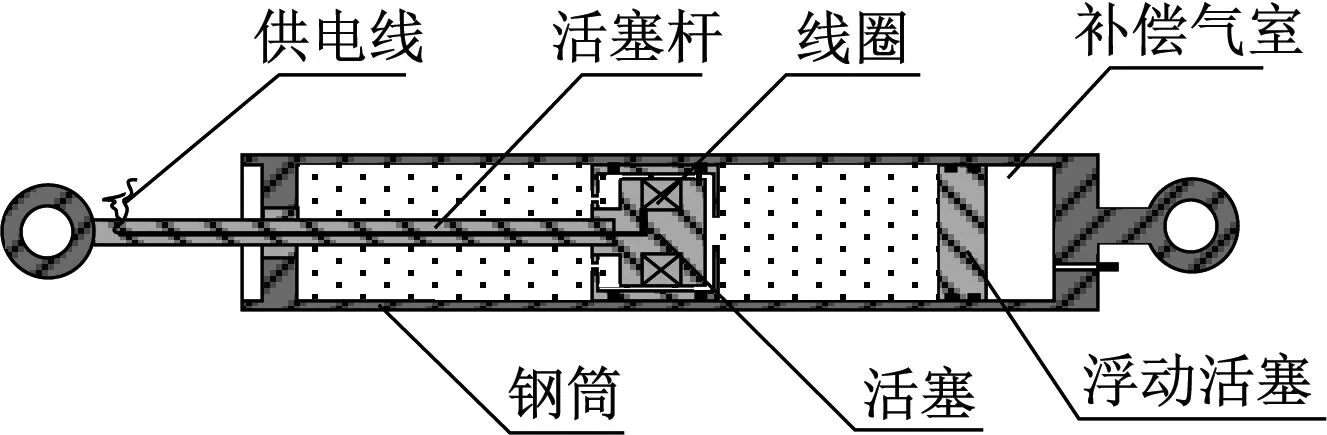
图1 MRD结构图

1.2 MRD性能试验

MRD性能试验系统如图2所示。系统主要由力传感器、相对位移传感器、数据采集仪、程控电流源、传感器供电电源、数据采集上位机、试验台及其控制上位机等组成。采用正弦激励，通过程控电流源改变加载在MRD线圈上的电流值及激振速度，测量力和位移值。设定电流值分别为0 A、0.1 A、0.25 A、0.5 A、1 A、1.5 A、2 A，速度值分别为0.05 m/s、0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s、0.52 m/s，正弦激励幅值A=0.025 m，数据采集频率f=2 048 Hz。

图2 MRD性能试验系统

试验得到数据后，位移信号经微分处理后变成速度信号，可得到各个工况下的阻尼力-位移及阻尼力-速度特性曲线。限于篇幅，给出0.05 m/s速度下的MRD阻尼特性曲线，如图3所示。

(a) 阻尼力-位移

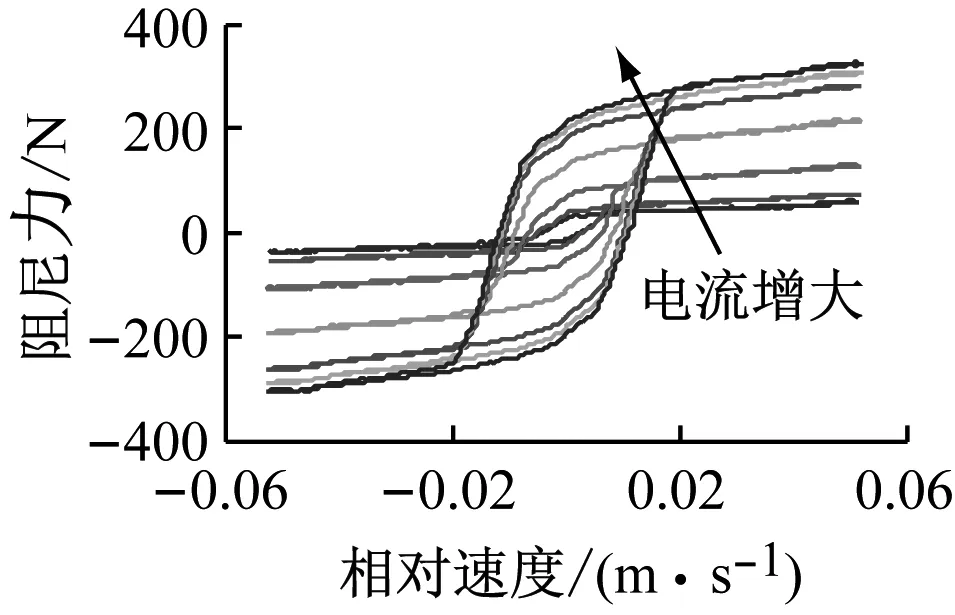
(b) 阻尼力-速度

图3可知，MRD示功曲线饱满，不存在“塌陷”现象，随着电流增加，示功曲线包围的面积增加，表明MRD耗功能力的增加，具备较好的耗功能力。电流在1 A以前，随着电流增加，阻尼力值的增长较为迅速，而在1 A以后，增长较为缓慢，表明磁场在1 A左右逐渐趋近饱和。

2 MRD力学模型的建立

2.1 双Sigmoid模型

图3可知，由于黏滞阻尼力的存在，MRD的阻尼力-速度呈现滞回特性，即在速度曲线在拉伸和压缩两种运动状态下并非完全重合，而是在速度趋近于0附近呈现出一个滞回环，滞环随着电流的增大而增大。阻尼力-速度特性曲线与S型生长函数Sigmoid函数的趋势十分相似。李秀领等[12]根据MRD滞回曲线中上下两分支形状的对称特性，利用双Sigmoid函数来构建MRD力学模型，双Sigmoid模型(Double Sigmoid Model, DSM)表达式为

(1)

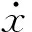
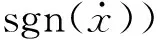
2.2 改进双Sigmoid模型

基于上述分析，在文献[12]提出的双sigmoid模型的基础上，考虑MRD建模存在的关键性问题，利用sigmoid曲线的准确建模特性，以及参数化滞回模型对低速滞回特性的建模准确性特性，提出改进型双sigmoid模型，其表达式为

(2)

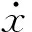
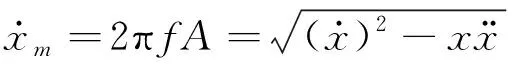
(3)

式中:A为振幅；f为激励频率。

改进双Sigmoid模型如图4所示。该模型包含双Sigmoid滞环模块、黏滞阻尼力模块cb、蓄能器刚度模块k0及偏置力模块f0。可弥补DSM的不足，待定参数7个，且不包含微分项，各参数意义明确，可方便编程实现，易于工程化应用。

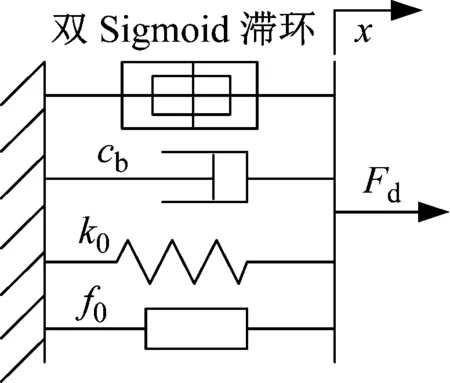
图4 改进双Sigmoid模型

2.3 参数含义及其对模型的影响分析

与双Sigmoid模型相比，改进双Sigmoid模型需要分析的关键参数包括换向符号sgn(x)、k、β、δ、k0及f0。

(1) sgn(x)对模型的影响

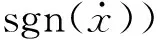
(2)k对模型的影响

分别令k为0.1k、k及10k，得到k对模型的影响如图6所示。图中可知，随着k的增加，在滞环转折处的曲线光滑度逐渐下降，因此，k的取值不宜过大。

(3)β对模型的影响

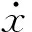
(4)δ对模型的影响

分别令δ为0.5δ、δ及2δ，δ对模型的影响如图8所示。与δ相反，随着δ的增加，滞环宽度逐渐增加，δ与x的方向有关，调节滞环宽度时，其与sgn(v)的乘积为定值，可保证一定的基础滞环宽度。通过改变β及δ的大小可使IDSM适应高速和低速条件下不同的滞环宽度需求。

图5 IDSM-sgn(x)与IDSM-sgn(v)的比较

图6 k对模型的影响

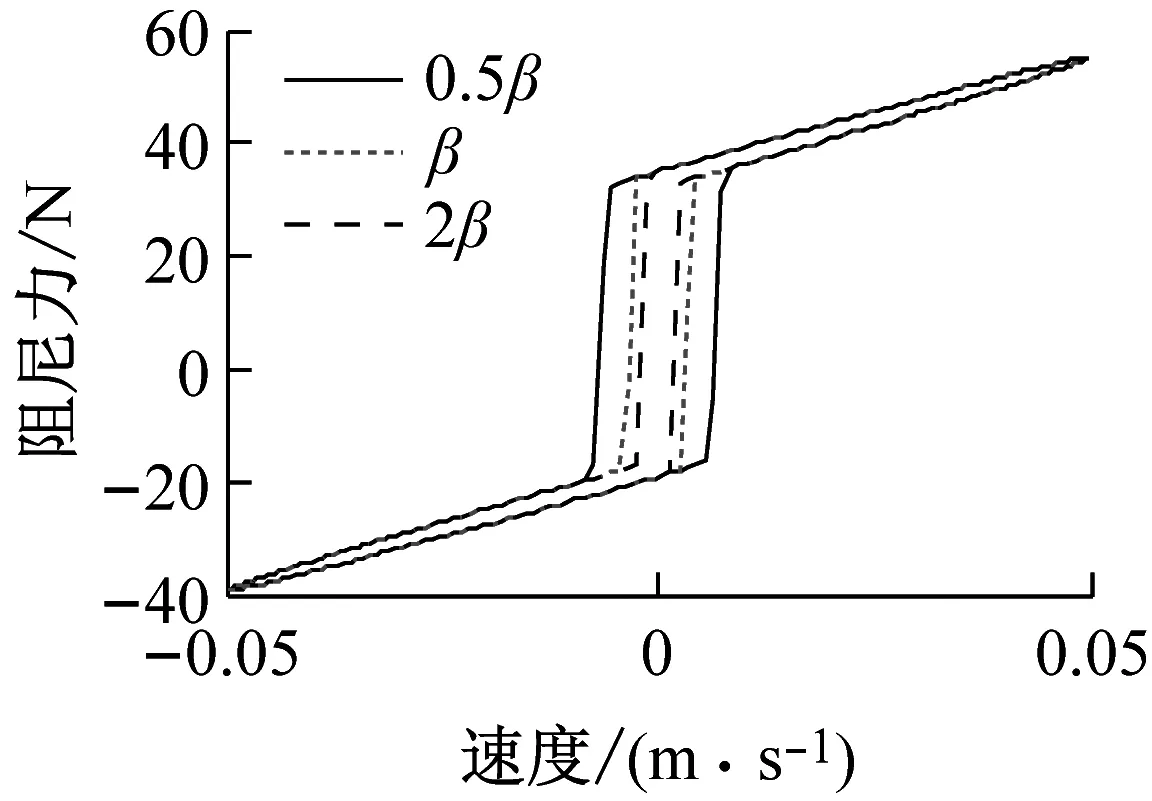
图7 β对模型的影响

(5)k0对模型的影响

分别令k0为0.5k0、k0及2k0，k0对模型的影响如图9所示。随着k0的增加，阻尼力屈服后的拉伸和压缩阻尼力差别逐渐增加，通过改变k0的大小可改变IDSM屈服后区的正逆曲线的高度差异，适应不同速度和电流下的差异需求。

(6)f0对模型的影响

分别令f0为0.5f0、f0及2f0，f0对模型的影响如图10所示。随着f0的增加，阻尼力偏置情况逐渐改善，通过添加f0可使IDSM阻尼力归零。

综上分析可知，sgn(x)、β、δ、k0及f0均会对MRD阻尼力模型产生影响，通过调节这些参数可以使模型满足不同条件下的MRD阻尼力建模需求。

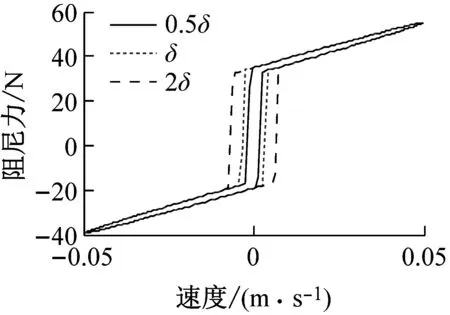
图8δ对模型的影响

Fig.8 The influence ofδon model

图9 k0对模型的影响

图10 f0对模型的影响

2.4 参数对比分析

为了进一步对比各参数对模型的影响，以及IDSM相比于DSM的建模优势，不失一般性，选择k0及f0两个参数作为对比。其中，原始试验数据得到的曲线命名为Original，DSM单独加上k0命名为DSM+k0，DSM单独加上f0命名为DSM+f0，DSM加上k0及f0命名为DSM+k0+f0(即IDSM)。电流为0 A，0.05 m/s速度条件下，阻尼力-位移及局部图、阻尼力-速度及局部图分别如图11、12所示。

(a) 全局图

(b) 局部图

(a) 全局图

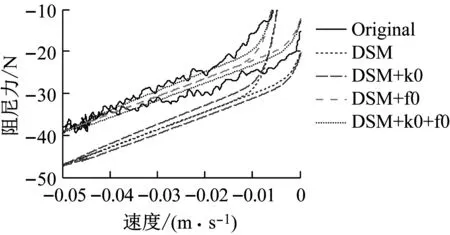
(b) 局部图

图11及图12可以看出，DSM与DSM+k0与Original相比存在偏置力，而DSM+f0及DSM+k0+f0增加了偏置力项f0之后，与Original的阻尼力在大方向上一致性较好。从Original可以看出，阻尼力在屈服后区的拉伸和压缩两个方向上，阻尼力大小不相等，DSM+k0及DSM+k0+f0由于增加了k0项，与Original存在较好的一致性。相比之下，DSM无k0及f0项，而IDSM不仅可消除偏置力带来的影响，且与Original的阻尼力拉伸和压缩状态下的大小差异存在较好一致性，建模精度得到提高。

2.5 各参数与电流及速度的关系

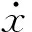
(e) cb (f) k0 (g) f0

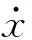
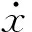
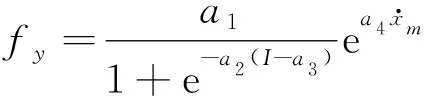
(4)

(5)

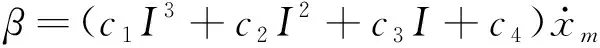
(6)

(7)

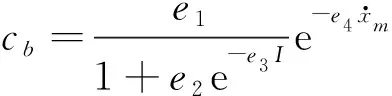
(8)

k0=f1I4+f2I3+f3I2+f4I+f5

(9)

(10)

参数辨识结果如图14所示。对比图13及图14可知，两幅图中对应参数图形的一致性较好，表明式(4)～(10)可较好地表示各参数与速度及电流之间的关系。

(a) fy

(b) k

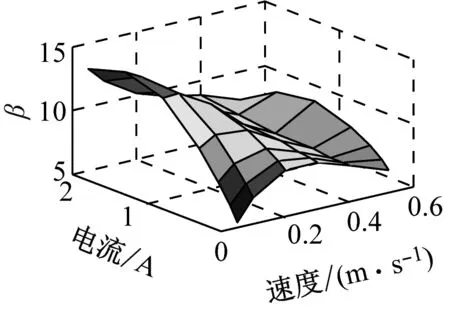
(c) β

(d) δ

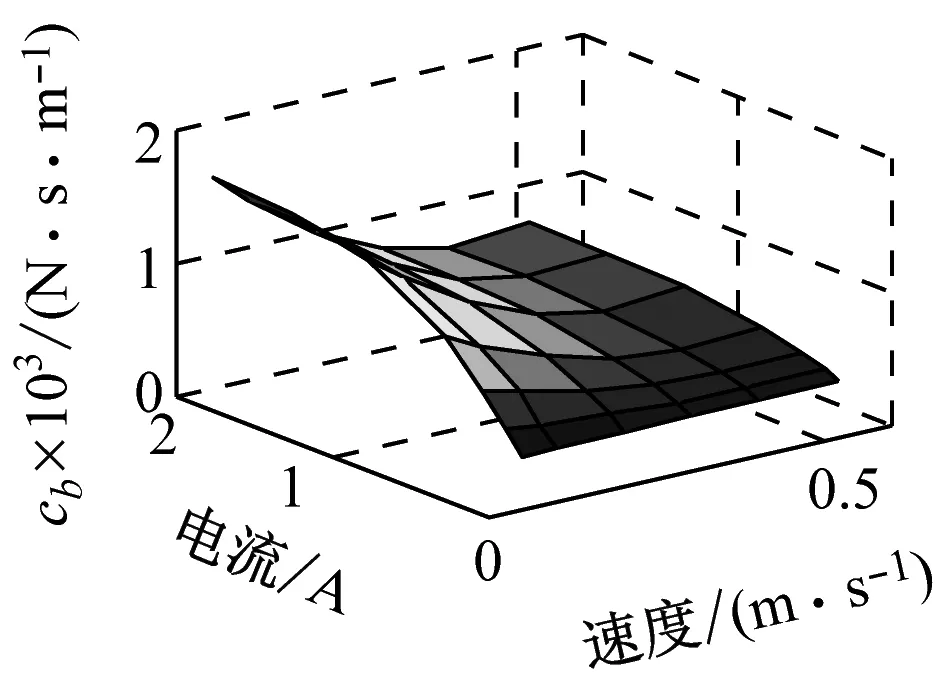
(e) cb

(f) k0

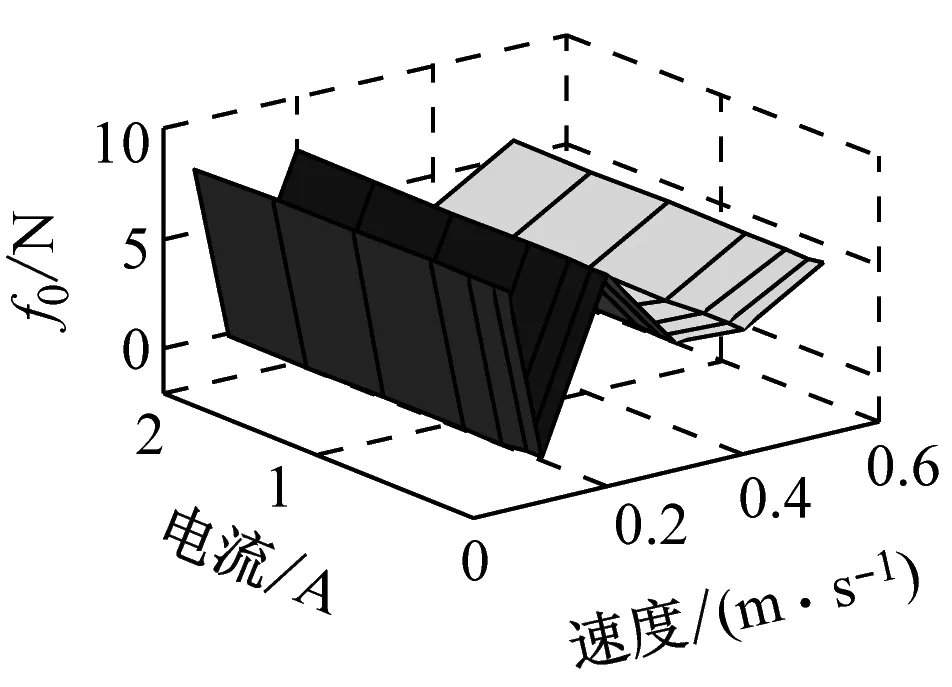
(g) f0

图14 各参数辨识结果

Fig.14 Identification result of each parameter

3 MRD力学模型的验证

MRD力学模型的验证包括拟合结果验证和模型预测验证两部分。其中，拟合结果验证是验证IDSM及拟合得到的各个参数与电流及速度的关系式的正确性；模型预测验证则是通过改变电流值，试验测量MRD阻尼力值，与仿真环境下建立的IDSM模型中，改变相同电流值时得到的MRD阻尼力值进行对比，验证模型的预测准确性。

3.1 拟合结果验证

不失一般性，试验结果中的低速0.05 m/s及高速0.52 m/s速度条件下，阻尼力-位移及阻尼力-速度的拟合值与试验值的对比分别如图15、16所示。阻尼力-位移示功图的曲线由内而外，加载电流依次增大，分别为0 A、0.1 A、0.25 A、0.5 A、1 A、1.5 A、2 A。图中的虚线代表试验值，实线代表拟合值。

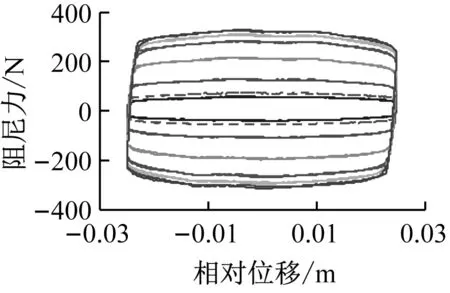
(a) 阻尼力-位移

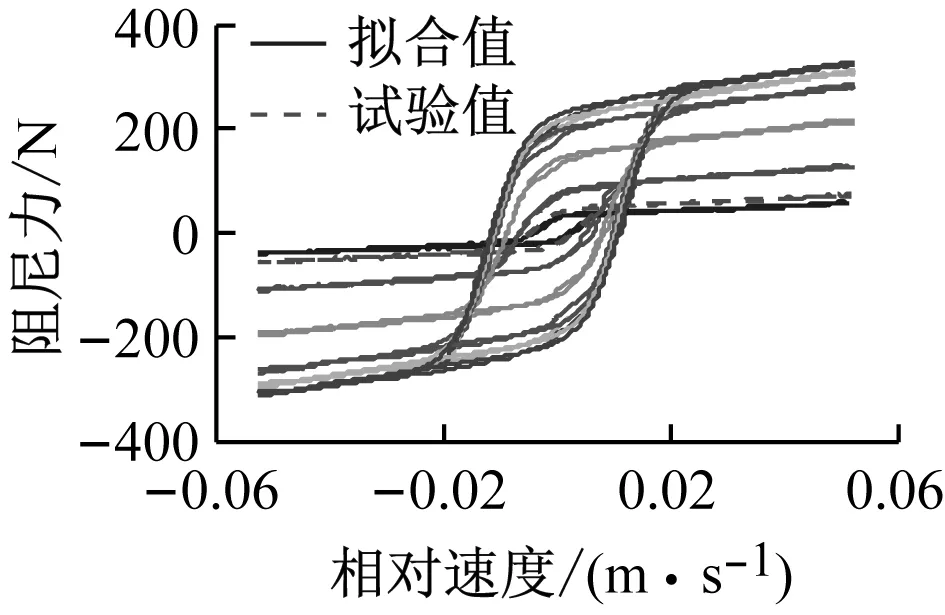
(b) 阻尼力-速度

(a) 阻尼力-位移

由图15及图16可知，不同的电流及速度条件下，IDSM与Original的拟合度均较好，拟合精度较高。表明在MRD可加载的最大电流值及最大速度下，IDSM均与试验结果具有较好的拟合度。

3.2 模型预测验证

设定振幅A=0.025 m，分别取电流值0 A、0.1 A、0.25 A、0.5 A、1 A、1.5 A、2 A，得到试验测量的阻尼力值，与在仿真环境下建立的IDSM模型，加载同等条件下的电流，得到的模型预测值。对比两阻尼力值，验证模型的准确性。阻尼力随电流的变化及其局部图分别如图17、18所示。

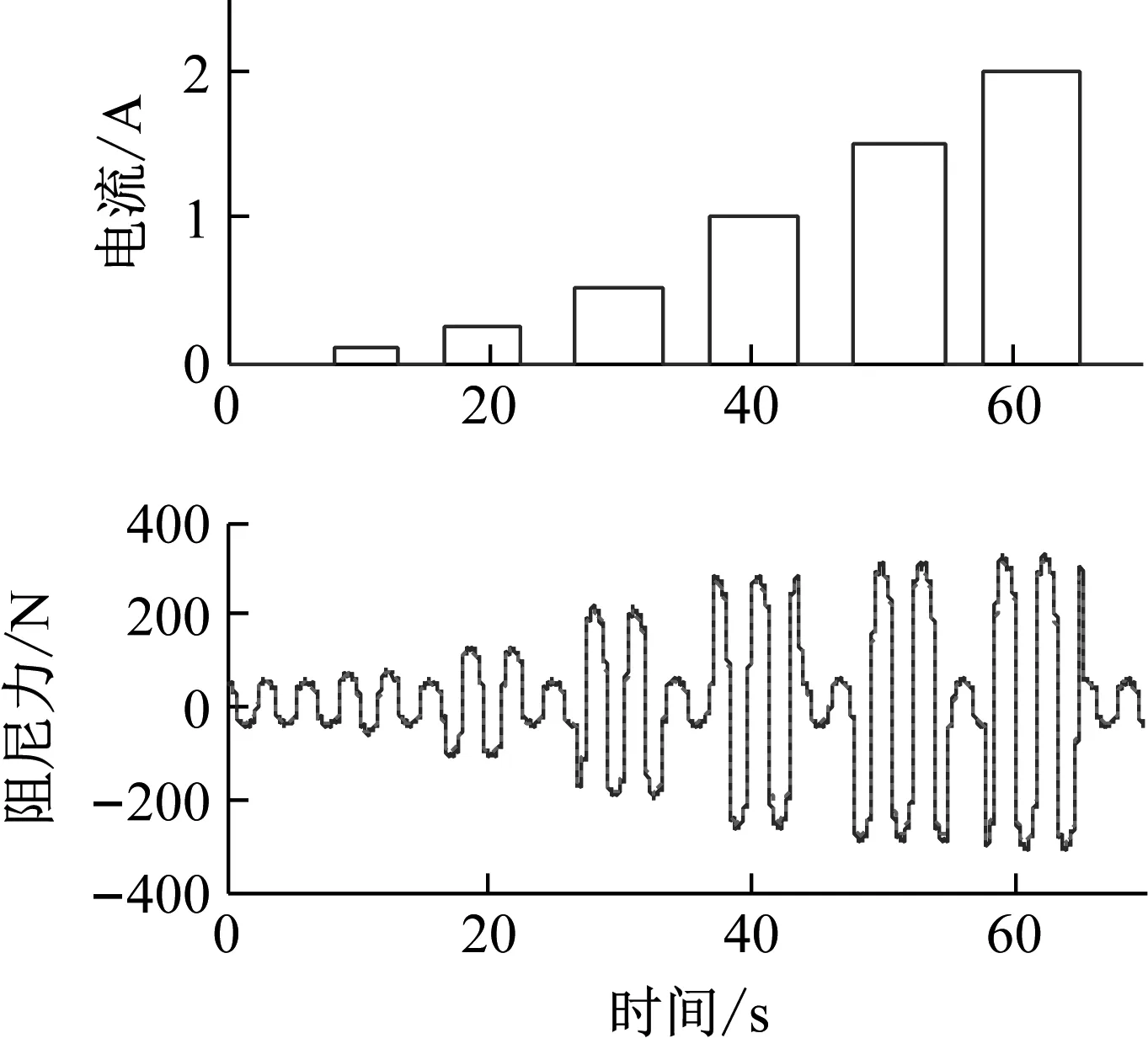
图17 阻尼力随电流的变化

图18 阻尼力随电流的变化局部图

图17及图18可知，模型预测值与试验值有较好拟合度，电流值较小的时候，拟合度更好，随着电流增大，拟合度稍有变差。统计学上，标准差可反映数据集的离散程度，利用标准差表示MRD试验阻尼力Ftest与模型预测阻尼力Fpredict之间的离散关系，阻尼力标准差σ表达式为

(11)

速度分别为0.05 m/s、0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s、0.52 m/s，电流0 A、0.1 A、0.25 A、0.5 A、1 A、1.5 A、2 A，得到σ与电流及速度的关系如表2及图19所示。

图19 σ与电流及速度的关系

图19可知，随着电流及速度的增加，MRD标准差σ随之增加，σ的最大值11.1 N，与此刻的阻尼力650 N之比，可得误差相对值为1.71%，可见该误差值较小，IDSM预测阻尼力较准确。

表2 σ与电流及速度的关系

4 结 论

本文对设计的MRD进行了性能试验，根据MRD阻尼特性建立了相应的力学模型，并对模型参数进行识别，对模型准确性进行了验证。可得如下结论：

(1) 该MRD的阻尼特性曲线表明，阻尼力呈非线性，随着电流增加，阻尼力增加，示功曲线包围面积随之增加，表明MRD耗功能力增加，具备较好的耗功能力；

(2) 相比于Bingham模型无法体现阻尼力非线性特性，以及Bouc-wen模型表达式复杂等，IDSM针对DSM存在的缺陷，考虑阻尼力与位移的关系、换向符号、蓄能器刚度及偏置力等因素的影响，提高了模型准确性；

(3) IDSM具有模型精确、表达式简洁、参数物理意义明确且易于编程实现等优点，在不同的电流和速度下，其模型精度均较好，适用于工程领域。