地震作用下辅助墩对斜拉桥支座脱空的影响

李永兴， 易 江， 李建中

(同济大学 土木工程防灾国家重点实验室，上海 200092)

近年来，为了适应大跨径结构的需要，斜拉桥在我国得到广泛应用[1]。由于结构形式特殊、跨度较大以及对交通工程的重要程度较高，斜拉桥的抗震性能一直是斜拉桥设计和建设过程中一项十分重要的课题[2-3]。

在地震作用下，斜拉桥的支座通常会承受较大的动轴力,有时甚至会发生支座脱空的现象[4]。为防止支座脱空现象的发生，在实际工程中通常采用主梁压重和设置拉力摆等方法来解决[5-6]。黄莹颖等[7]研究了PC斜拉桥拉压支座失效的影响因素，指出在设有辅助墩拉压支座的PC斜拉桥中，拉压支座能起到改善结构受力状态的关键性作用；李宏江等[8]对斜拉桥辅助墩拉力摆断裂的成因进行了分析，指出主梁与辅助墩之间的压力储备不足和钢丝锈蚀、疲劳是导致拉力摆抗拉支座静载失效的重要原因；然而目前这些措施还较少考虑到地震因素的影响。

当斜拉桥边孔设在岸上或浅滩，边孔高度不大或不影响通航时，通常在边孔设置辅助墩，以改善结构的受力状态，提高施工阶段的安全[9]。杨希尧等[10]研究了辅助墩对独塔斜拉桥静力和动力特性的影响；喻梅等[11]研究了辅助墩对不同结构布置的四塔斜拉桥静力行为的影响；孙利民等[12]对大跨度斜拉桥耗能型辅助墩的抗震性能进行了试验研究；但是针对于地震作用下辅助墩对斜拉桥支座脱空的影响还较少涉及。

本文以一座实际的双塔斜拉桥为背景工程，建立了拉压支座模型和支座脱离模型，研究了地震作用下斜拉桥过渡墩、辅助墩和主塔处支座的竖向受力特点和支座脱空现象，以及支座脱空对斜拉桥整体地震响应(梁体纵向位移和塔底弯矩)的影响；分析了辅助墩的数量和成桥压力对支座脱空的影响；最后对拉压支座的设计以及较易发生支座脱空的位置进行了说明。

1 背景工程和有限元模型

1.1 背景工程

泉州湾大桥是采用半漂浮体系的双塔双索面斜拉桥，跨径分布为70 m+130 m+400 m+130 m+70 m=800 m，图1给出了大桥的总体布置图。其中，T1和T2为带曲线造型的H形混凝土桥塔C50混凝土桥塔，承台以上塔高160.25 m，塔底两塔柱中心距为17.3 m。主梁为全封闭流线型钢混组合梁，梁高4.3 m，宽21 m(含风嘴)，钢材为Q370，混凝土为C55，在桥墩和主塔处，均采用纵向活动球钢支座。

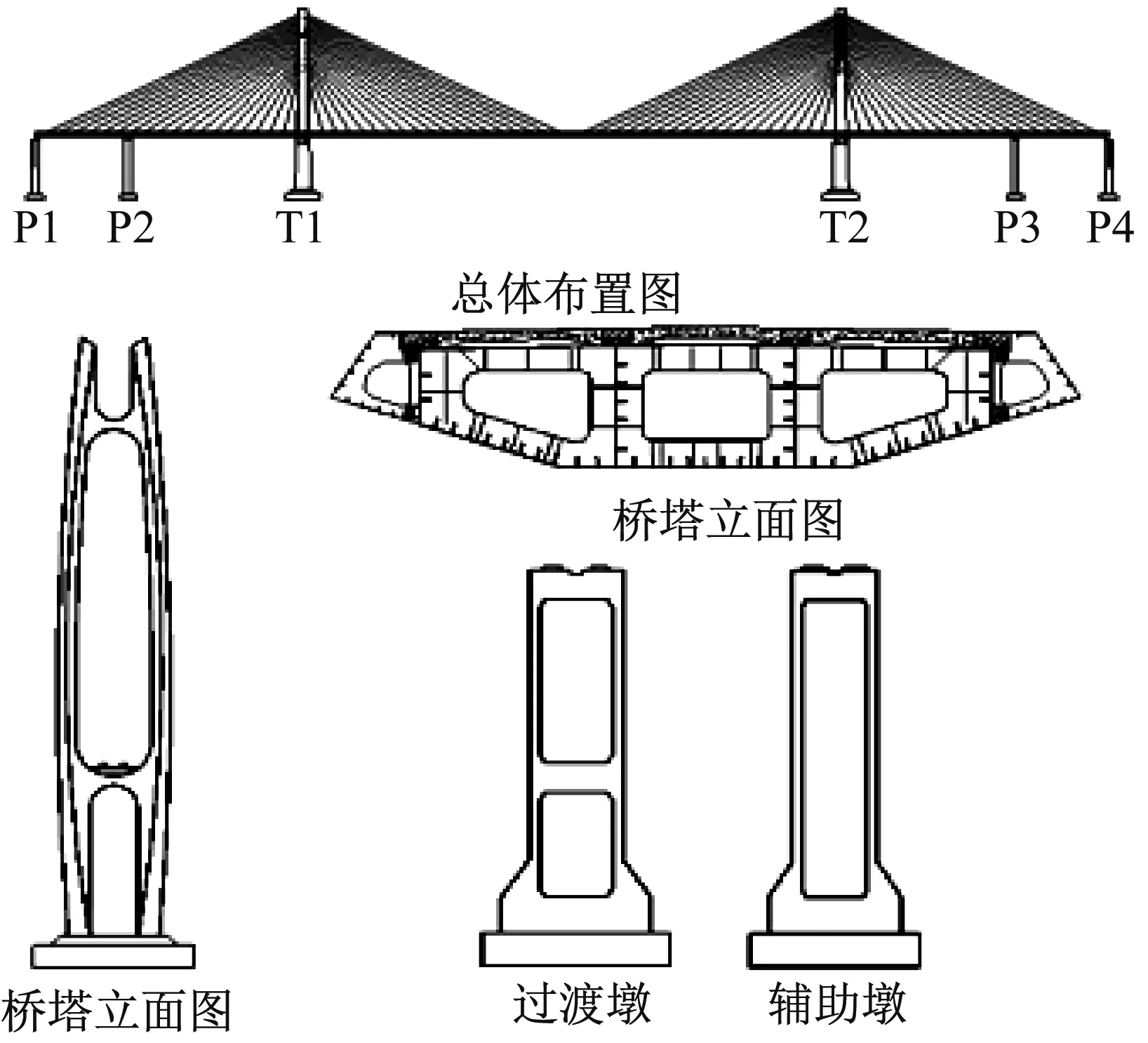
图1 泉州湾大桥总体布置图

全桥共采用8×18=144根斜拉索支承主梁，拉索为平行钢丝索，材料拉压强度为1 970 MPa。两侧过渡墩和辅助墩均为独柱墩，墩高50 m，混凝土材料为C45。每个过渡墩、辅助墩和主塔上均布置两个球型钢支座。其中主塔处的支座放置于横梁，过渡墩和辅助墩处的支座放置在墩柱顶部中心两侧，支座横向中心距为12.8 m。主梁纵向自由滑动，横向固定。静力分析表明，在成桥状态下过渡墩支座竖向压力为3 138 kN，辅助墩支座竖向压力为8 769 kN，塔柱处支座竖向压力为6 278 kN。

1.2 有限元模型

采用结构分析程序SAP2000建立背景工程的全桥三维非线性有限元模型[13]，具体建模方法如下：

在模型中，主梁、主塔、桥墩、承台采用梁单元模拟，斜拉索采用杆单元模拟。主塔和主梁考虑了考虑单元初始内力对几何刚度矩阵的影响(P-Delta效应)，斜拉索采用Ernst公式计算等效弹性模量来考虑拉索的垂度效应。主塔塔底、各墩底均固定约束，不考虑基础对全桥地震响应的影响。过渡墩、辅助墩和主塔处的纵向滑动支座采用理想弹塑性连接单元模拟，支座摩阻系数取0.02。根据《公路桥梁抗震设计细则》[14]，斜拉桥的结构阻尼比取0.03。另外，根据是否模拟支座脱离现象，对背景工程建立了两个模型,见图2。

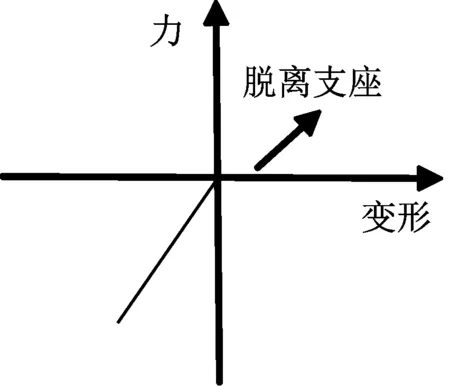
(a) 脱离支座

(b) 拉压支座

(1) 脱离模型：假设支座不能承受拉力，只能承受压力，如图2(a)所示。支座竖向采用线性弹簧碰撞模型[15]模拟主梁与支座的脱离-接触过程。对于线性弹簧碰撞模型的碰撞刚度如何取值目前尚无确切定论，为了防止碰撞体之间发生侵入现象，在碰撞模拟中通常需要设置较大的碰撞刚度，但过大的碰撞刚度不仅会带来数值的计算稳定性问题，而且分析结果中还会出现失真的巨大撞击力[16]。参考以往相关研究[17]，本文取gap单元刚度k为 1×106kN/m。单元间隙取为0。对于碰撞过程中的能量损耗，禚一等[18]指出对于弹性恢复系数较高、近似弹性碰撞的情况，碰撞过程中的能量损失对计算结果影响不大。而且由于碰撞阻尼参数的选取目前缺少一致性结论且限于程序功能，本文未考虑碰撞时的能量耗散。

(2) 拉压模型：假设采用拉压支座，支座能承受拉力和压力，且受拉刚度与受压刚度相同当支座与梁体接触后，可以认为是刚性支撑。支座竖向采用线性弹簧模型，如图2(b)所示。

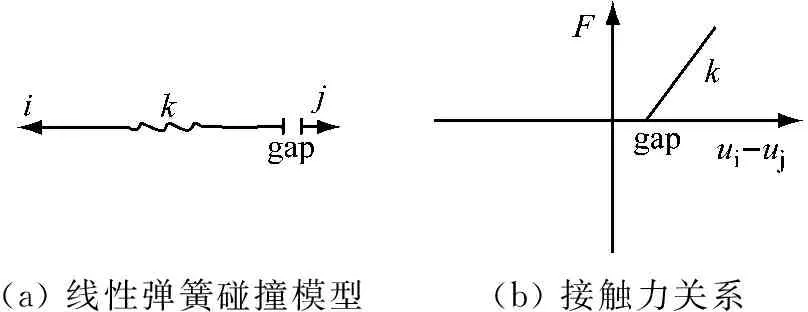
(a) 线性弹簧碰撞模型(b) 接触力关系

图3 碰撞单元模型

Fig.3 Pounding element model

在非线性模型中考虑球形钢支座的相对滑动效应，用双线性模型对其进行模拟，如图4所示。球钢支座的屈服力Fy为：

Fy=Nμ

(1)

式中:N为支座的竖向反力；μ为摩擦因数，根据《公路桥梁抗震设计细则》取0.02。双线性模型中取初始滑动位移xy为2 mm，并由此计算初始刚度。

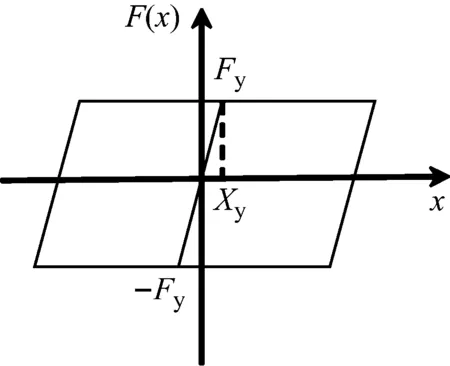
图4 球钢支座的双线性模型

球钢支座的布置示意图如图5所示，过渡墩和辅助墩处的球钢支座放置在墩柱顶部中心两侧，一侧为双向滑动，一侧为纵向滑动；主塔处的球钢支座均为双向滑动支座。

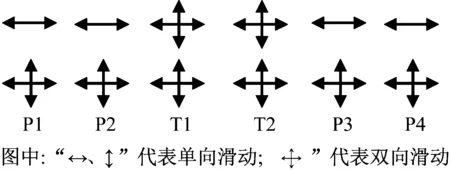
图5 球钢支座布置示意图

脱离模型和拉压模型的支座竖向模拟见图2。由此可见，对于脱离模型，当支座的变形为正值时，支座竖向反力为0，表明支座出现了脱空现象。在支座脱空前，脱离模型与拉压模型相同；在支座脱空后，两个模型有所差异。对于两个模型，在进行时程分析前，先进行自重分析，确保时程分析初始状态为斜拉桥的成桥状态[18]。图3给出了全桥有限元模型示意图。为了更好地了解斜拉桥支座的脱空现象，表1给出了泉州湾大桥的前10阶动力特性,采用支座的初始刚度计算结构的自振周期。

在结构的前10阶阵型中，第一阶阵型为主梁纵飘，另有五阶阵型与主梁的竖弯有关，与主梁纵飘及竖弯有关的阵型示意图如图6所示。当主梁发生纵飘、正对称或反对称竖弯时，主梁的挠曲形状中出现显著的竖向挠曲变形，在纵向+竖向地震作用下，主梁会发生明显的竖向位移，从而引起支座产生较大的竖向力，当支座承受的拉力大于预压力时，便会发生脱空现象。

1.3 地震动输入

根据场地地震危险性分析，大桥场址为Ⅲ类场地土，50年超越概率2%对应的地面加速度峰值为0.40 g。从太平洋地震工程中心(Pacific Earthquake Engineering Research Center，PEER)的地震波数据库选择了8条Ⅲ类场地的实际地震波，且将加速度峰值调整为0.40 g，作为水平向地震动输入，地震波的详细信息见表2。

表1 泉州湾大桥动力特性

Tab.1 Property of the dynamic behaviors of Quanzhou Bay bridge

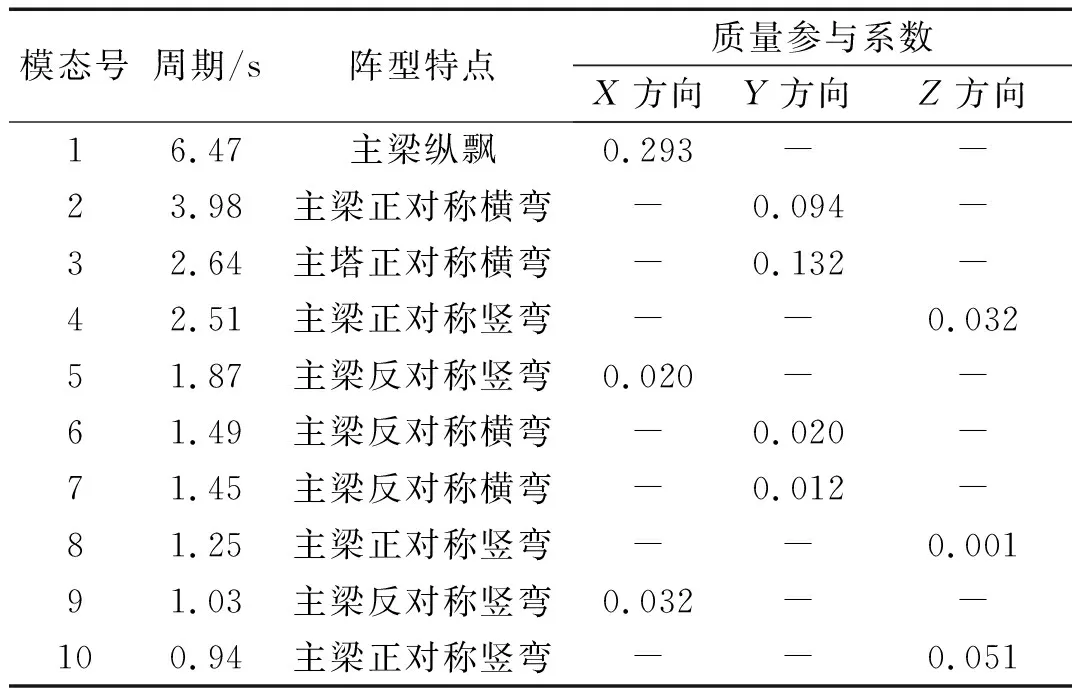
模态号周期/s阵型特点质量参与系数X方向Y方向Z方向16.47 主梁纵飘0.293 --23.98 主梁正对称横弯-0.094 -32.64 主塔正对称横弯-0.132 -42.51 主梁正对称竖弯--0.032 51.87 主梁反对称竖弯0.020 --61.49 主梁反对称横弯-0.020 -71.45 主梁反对称横弯-0.012 -81.25 主梁正对称竖弯--0.001 91.03 主梁反对称竖弯0.032 --100.94 主梁正对称竖弯--0.051

(a) 主梁纵飘

(b) 正对称竖弯

(c) 反对称竖弯

Fig.6 Longitudinal drift and vertical bending mode shape of the main beam

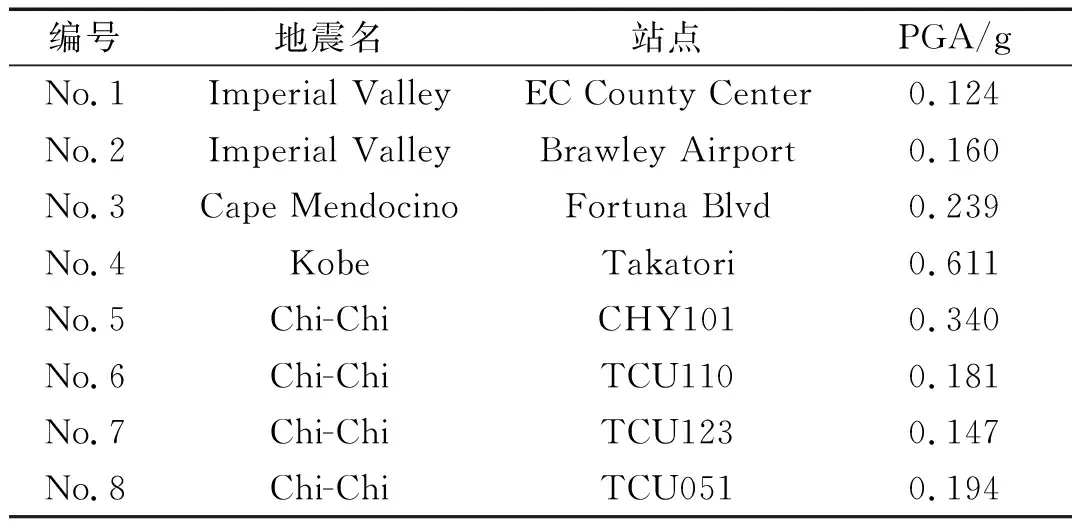
表2 选择的实际地震波

另外，在斜拉桥抗震设计时还应考虑竖向地震动的影响，根据《公路桥梁抗震设计细则》，竖向地震动取为水平地震动的0.65倍，水平地震动的输入方向为纵桥向。

由于本文研究的重点为地震作用下的支座脱空效应，在分析中假设桥墩保持弹性，表3给出了8条地震波输入下桥墩的平均地震反应。计算结果表明，当8条波的地震加速度调整为0.4 g时，过渡墩、辅助墩和主塔塔底截面保持在弹性范围内工作。

表3 地震作用下脱空模型的墩底和主塔底截面验算

Tab.3 Checking calculations of the bottom of the piers and the main towers under selected earthquakes

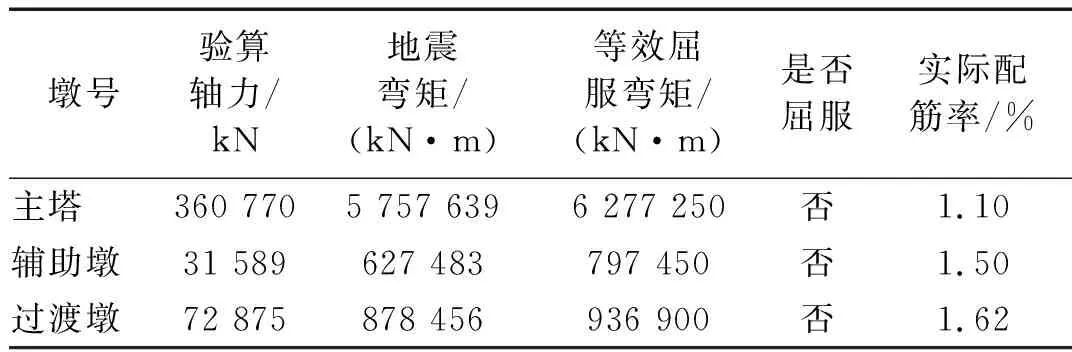
墩号验算轴力/kN地震弯矩/(kN·m)等效屈服弯矩/(kN·m)是否屈服实际配筋率/%主塔360 7705 757 6396 277 250否1.10辅助墩31 589627 483797 450否1.50过渡墩72 875878 456936 900否1.62

2 支座脱空现象

2.1 支座竖向反力

考虑到结构的对称性，本文中的计算结果均取半跨的地震响应。以No.1波为例，图7给出了支座脱离模型和支座拉压模型两个模型的支座竖向反力时程(以受压为正)。从图7支座脱离模型结果可知，在No.1波作用下，过渡墩、辅助墩和主塔处支座的竖向反力多次减小到0，表明出现了支座脱空现象。P1、P2和T1墩出现支座脱空现象的次数分别为5次、3次和3次。出现支座脱空后，梁体与支座脱离，支座竖向反力保持为0；当梁体与支座再次接触时，由于梁体与支座的碰撞，支座竖向压力迅速增加至较大的数值，如P1墩处支座竖向压力最大为23 368 kN(时间9.05 s)，达到支座恒载压力的7.45倍。对于拉压模型，P2、T1墩处支座反力在部分时刻出现负值，表明支座承受了拉力。对比两个模型，脱离模型由于考虑了梁体与支座碰撞，各墩柱支座压力最大值均大于拉压模型，如P1、P2和T1墩处支座最大压力分别为拉压模型的3.13、1.69和1.48倍。表4给出了8条地震波作用下，脱离模型支座的最大压力。脱离模型的P1、P2和T1墩支座压力的最大值分别达到76 362 kN、93 606 kN和28 048 kN，相当于24、10.7和4.5倍的支座成桥压力。在实际工程中，较大的支座压力可能超过支座竖向设计承载力，支座将受损。表4结果还表明，由于碰撞的影响，不同地震波作用下支座最大压力离散性较大，如P2墩支座最大压力变化范围在46 259～93 606 kN之间。

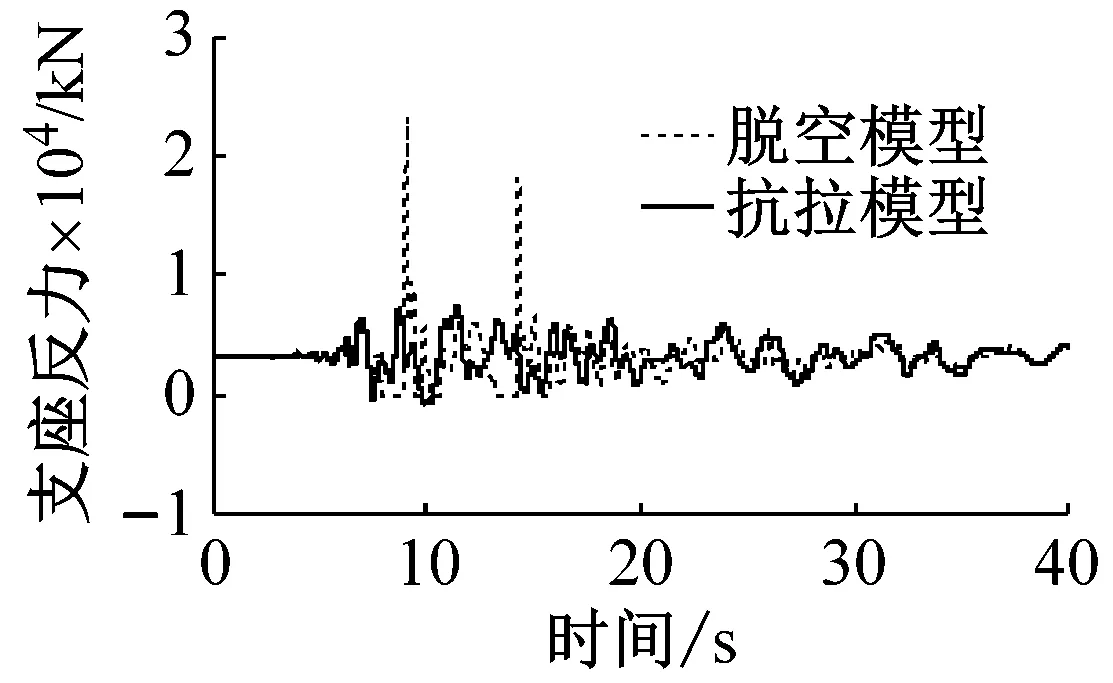
(a) 过渡墩

(b) 辅助墩

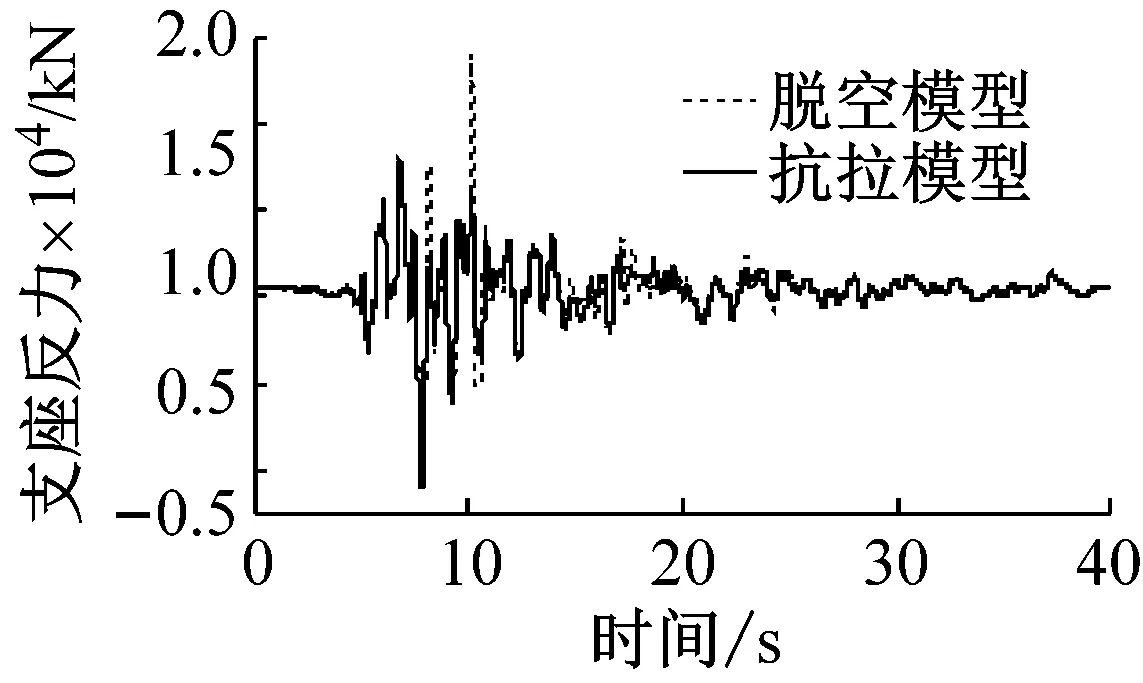
(c) 主塔

图7 No.1波作用下支座竖向反力时程

Fig.7 Time histories for vertical bearing force under No.1 wave

2.2 梁体竖向位移响应

支座脱空后，支座处梁体将产生向上的竖向位移。图8给出了脱离模型在No.1波作用下P1、P2和T1处主梁竖向位移响应时程，表5给出了8条地震波作用下塔、墩处梁体竖向位移幅值。从图8可知，在支座脱空阶段，T1主塔处梁体竖向位移较小，不超过0.07 m，每次支座脱空持续时间较短，不超过0.3 s。而P1、P2墩处支座脱空持续时间较长，梁体竖向位移可以发展到很大，如P2墩处第一次支座脱空持续了近2.57 s，梁体竖向位移达到0.65 m。P1和P2墩处支座脱空后梁体竖向位移普遍较大，位移均值都超过了0.7 m。由于碰撞的影响，不同地震波作用下梁体的竖向位移响应离散性较大，如P1墩处梁体竖向位移变化范围在0.383～1.577 m之间，相差较为明显。

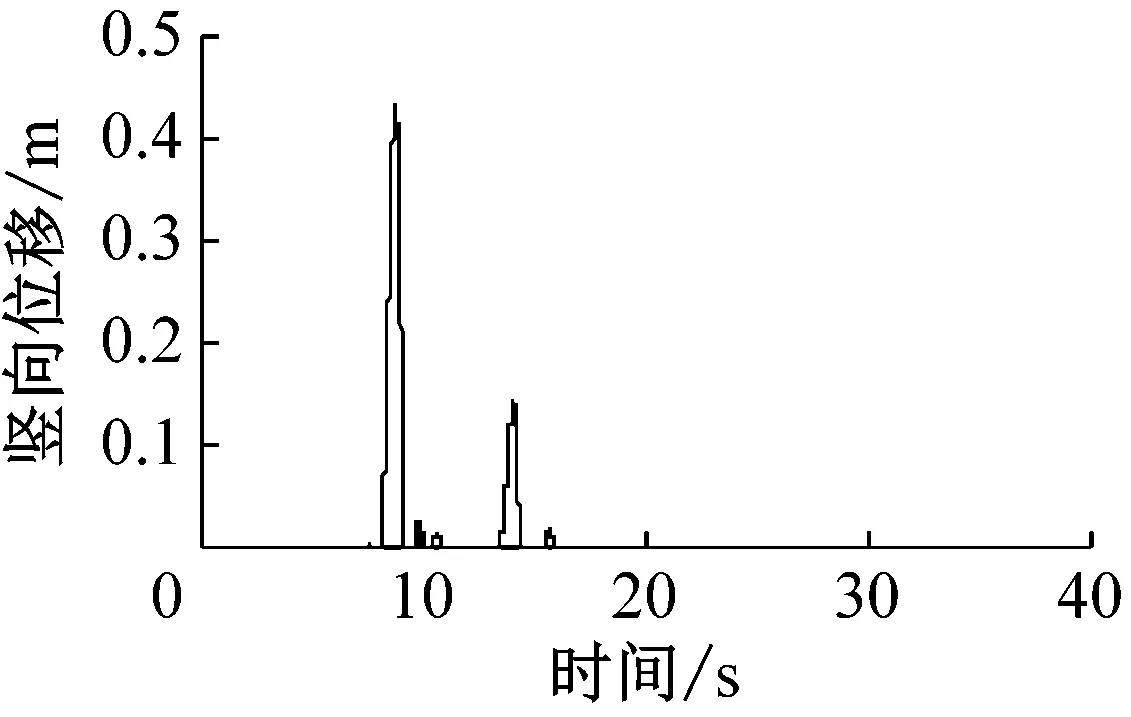
(a) 过渡墩

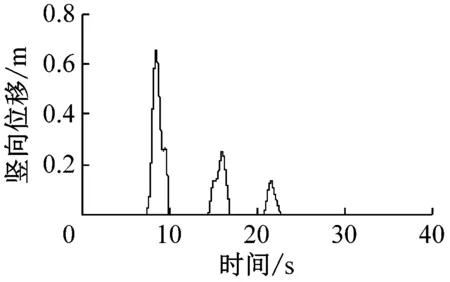
(b) 辅助墩

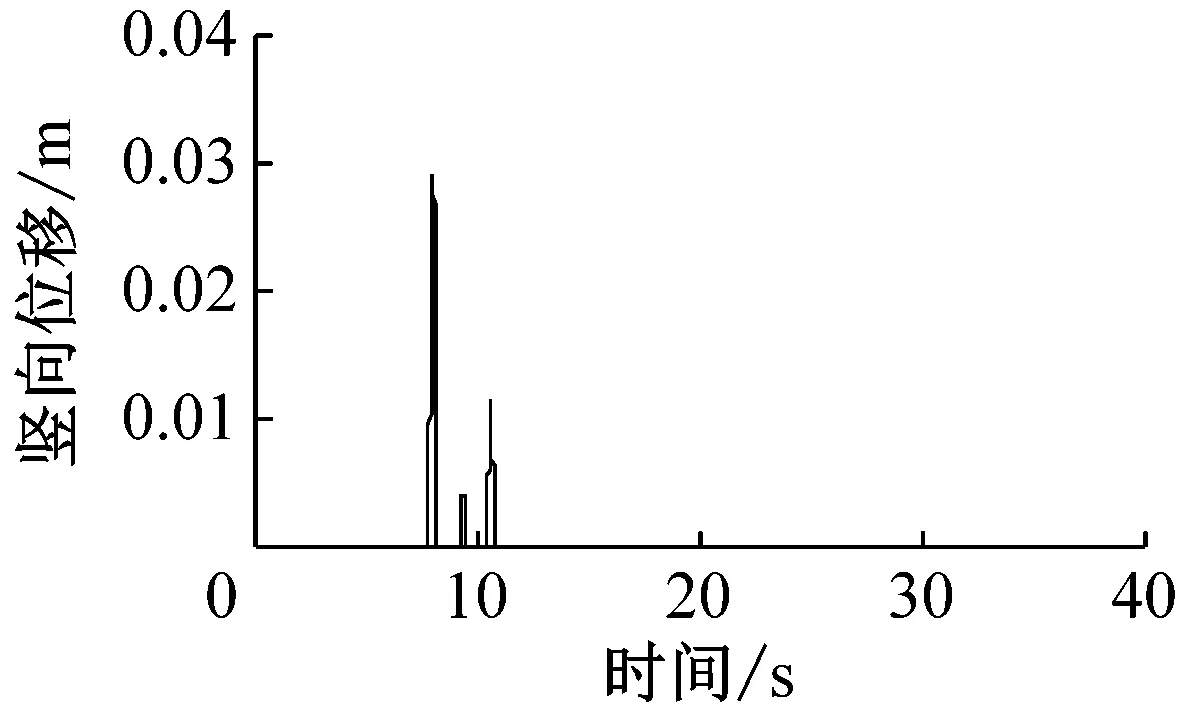
(c) 主塔

图8 No.1波作用下脱离模型支座处梁体竖向位移时程

Fig.8 Time histories for girder vertical displacement at bearing locations under No.1 wave of unseating model

2.3 不同位置处支座和梁体地震响应对比

由表5可知，T1主塔处的主梁竖向位移较小，均值仅为0.039 m，而脱离模型的P1过渡墩和P2辅助墩的竖向位移可以发展到很大，在P1过渡墩处甚至达到了1.577 m。总体来讲，P1过渡墩和P2辅助墩的主梁竖向位移较为相近，位移均值分别为0.865 m和0.700 m，但是由于两墩的位置关系，辅助墩处于过渡墩和主塔的中间位置，而过渡墩处于斜拉桥主梁的端部，且辅助墩处的成桥压力大于过渡墩处的成桥压力，所以当两墩处梁体的竖向位移相近时，辅助墩处梁体与支座产生的碰撞力要大于过渡墩处支座的最大压力，由表4可知：P2墩处的最大支座压力均值达到P1墩处最大支座压力均值的1.48倍。由此可见，相比于过渡墩和主塔，辅助墩为支座受压的最不利位置，在支座设计和选型中应重点关注。

表4 脱离模型支座竖向反力幅值

表5 脱离模型支座处梁体竖向位移幅值

2.4 支座脱空的影响

支座脱空后，斜拉桥边界条件发生变化，结构地震响应将异于不考虑支座脱空的结果。以No.1波为例，图9给出了脱离模型塔底弯矩和梁端纵向位移响应时程曲线，并与拉压模型比较。根据图9可知，当结构第一次支座脱空时(P2墩、时间7.3 s)，由于支座脱空较为明显(脱空持续时间为2.57 s，脱空后梁体与支座碰撞力达到53 482 kN)，脱离模型塔底弯矩和梁端位移时程开始逐渐偏离于拉压模型。此后，随着地震输入时间的增长，两个模型时程响应差异逐渐增加。但总体来看，时程曲线的变化趋势和峰值是比较接近的，由此可见，支座脱空只是结构局部响应的变化，对塔底弯矩和梁端的纵向位移影响较小。

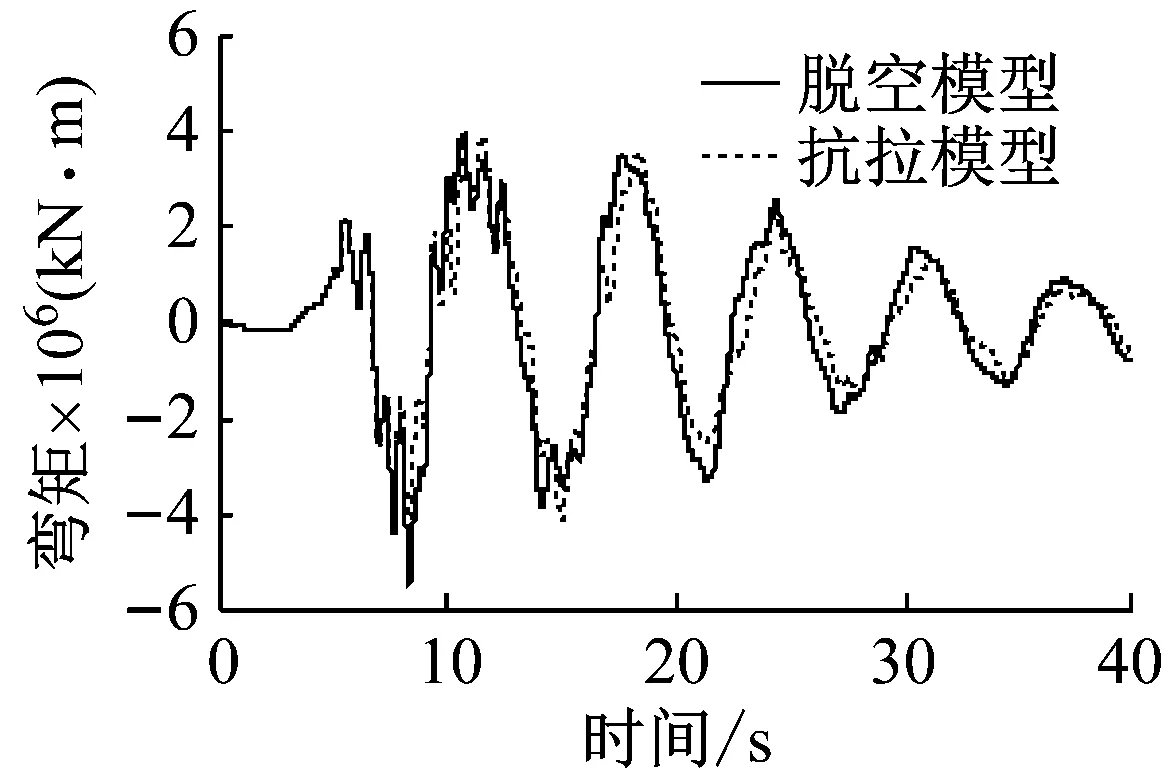
(a) 塔底弯矩

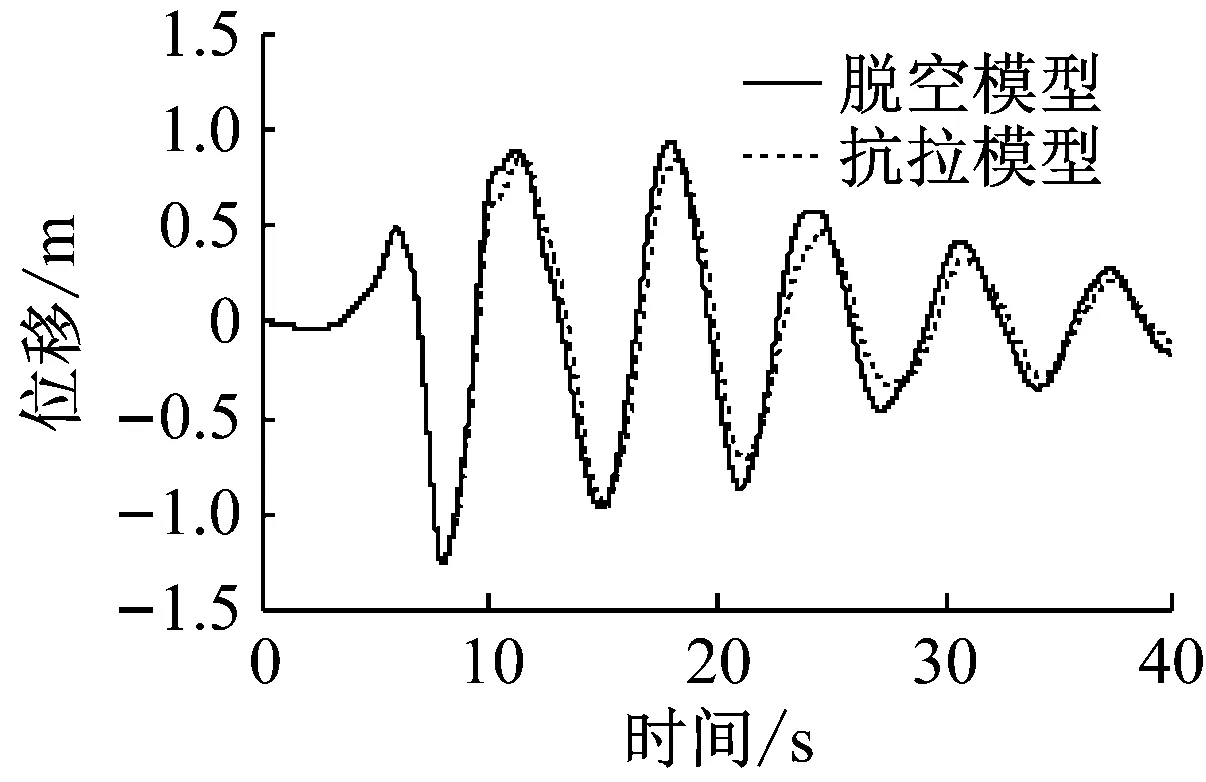
(b) 梁端纵向位移

Fig.9 Influence of unseating on the seismic responses of the structure

2.5 支座脱空的危害

根据以上分析可以得知，地震中斜拉桥发生支座脱空后，将产生较大的支座压力和支座处梁体的竖向位移，可能导致如下震害：

(1) 支座破坏。支座脱空后由于梁体与支座碰撞，产生的强烈碰撞力可能会超过支座的竖向承载能力，造成支座的破坏。

(2) 梁体破坏。当斜拉桥支座发生脱空后，主梁在竖向会产生较明显的位移和震颤现象，造成梁体铺装层等桥面结构的损坏，严重影响桥梁的安全使用性能及通车运营。另外，主梁与支座之间较大的碰撞力可能会导致支座处梁体发生结构性损坏，甚至造成主梁的开裂。

(3) 墩柱损坏。对于存在横梁的双柱墩结构，由于支座一般设置在横梁上，较大的支座压力可能会导致横梁出现剪切裂缝[19]。当支座与墩柱中心线之间存在偏心时，碰撞力使得墩柱产生较大的附加弯矩，严重影响过渡墩和辅助墩的安全性能。

考虑到以上支座脱空所导致的震害，在实际设计中应采用一定的抗震措施来避免支座发生脱空，如对主梁进行一定的压重、采用拉力摆索等抗拉支座来限制主梁发生脱空现象。

3 辅助墩对支座脱空的影响

对于双塔斜拉桥和多塔斜拉桥，通常在边孔设置辅助墩以改善结构的受力状态，当辅助墩受压时，辅助墩的设置可以减少边孔主梁弯矩，而受拉时则可以减少中跨主梁的弯矩和挠度，从而大大提高全桥的刚度。本节主要研究了斜拉桥在地震作用下辅助墩对支座脱空的影响。

3.1 辅助墩数量的影响

对于斜拉桥而言，在边孔设置辅助墩，对拉索在恒载作用下的受力影响很小[11]，为了评估辅助墩的数量对支座脱空的影响，本节在原脱离模型的基础上对辅助墩进行了调整，保持原有索力不变，通过在辅助墩处的压重来实现支座的成桥压力。为了方便起见，以下将将原模型去除辅助墩后的模型称作模型一(共0个辅助墩)，将泉州湾大桥的原模型(共2个辅助墩)称作模型二，将原模型增加辅助墩后的模型称作模型三(共4个辅助墩)。模型一、模型二和模型三的立面图如图9所示，其中模型三增加的两辅助墩由左向右分别命名为F1和F2墩，新增辅助墩的成桥压力为5 500 kN。

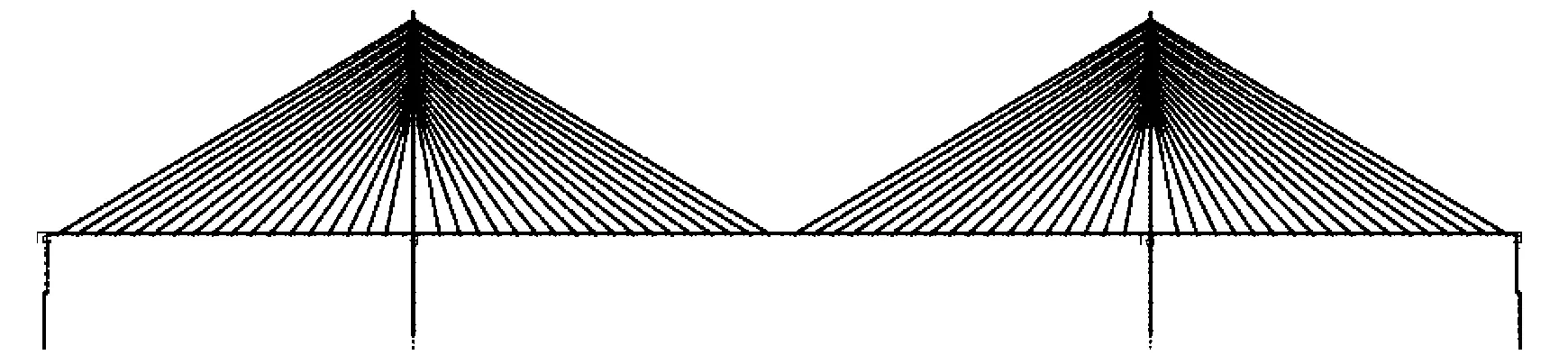
(a) 模型一

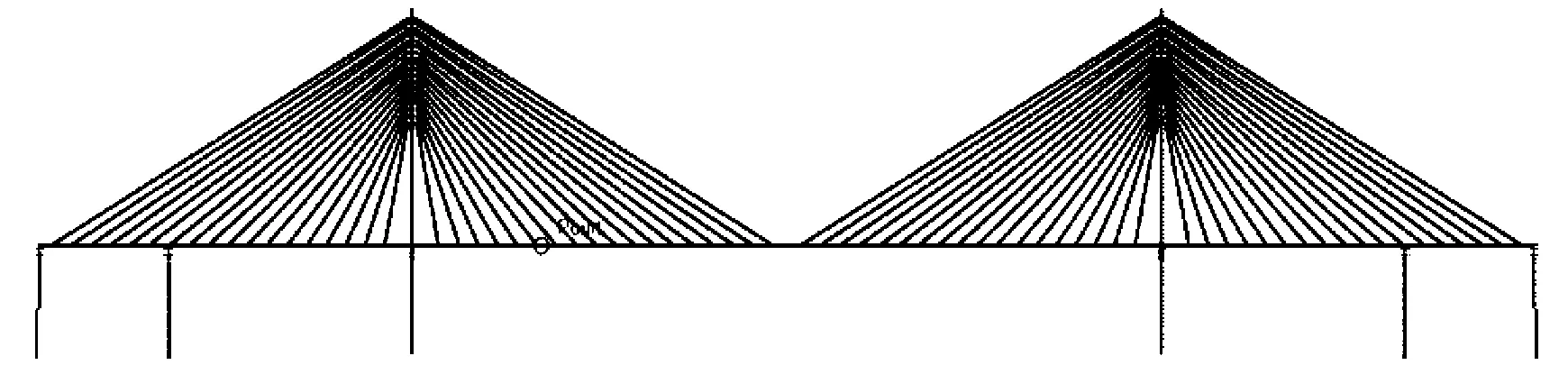
(b) 模型二

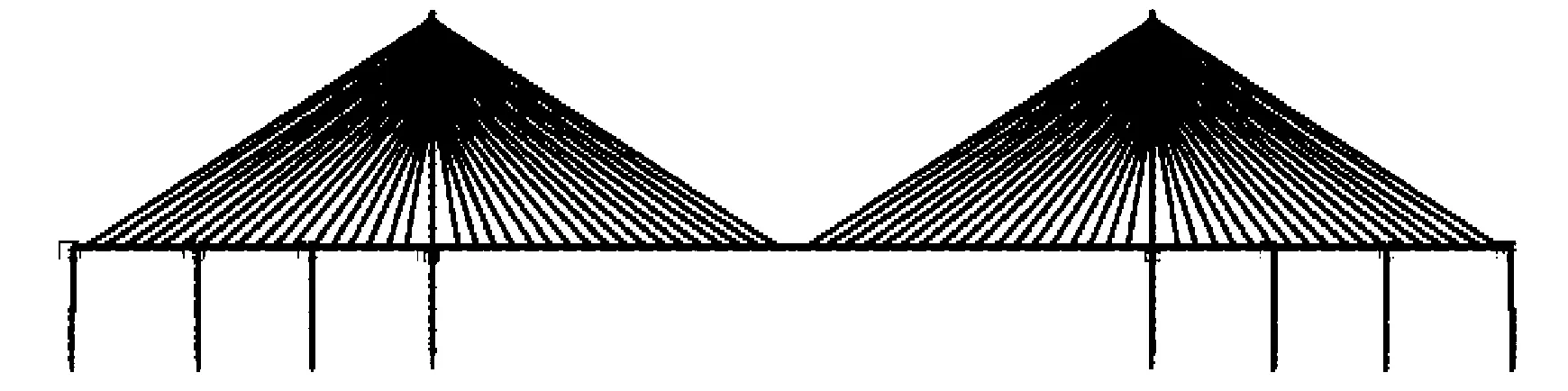
(c) 模型三

图11给出了三模型在NO.1波作用下主梁沿纵桥向的竖向峰值位移曲线图，图中表示的竖向位移均为主梁的上拱位移。由图11可知，当斜拉桥在左右两边跨各增加一辅助墩后，边跨跨中和中跨跨中位移降低了45%左右；当左右两边跨各增加两个辅助墩后，主梁的竖向峰值位移有所减小，但是位移变化相对较小，相对于模型二，模型三的边跨跨中位移仅降低了12%；主梁的竖向峰值位移在主塔中心线处达到最小，而边跨跨中和中跨跨中位置主梁的竖向位移较大。

为了进一步说明此现象，本文在主梁(半跨)上选取了四个控制点：0 m、70 m、133 m和400 m位置处，分别对应斜拉桥P1、P2、F1墩和中跨跨中位置，分别计算了三种模型在选取的8条地震动下的主梁竖向峰值位移，表6给出了7条地震动下模型二与模型一、模型三与模型二主梁控制点的竖向峰值位移比的均值。由表6可以看出，斜拉桥模型由0个辅助墩增加到2个后，主梁的竖向位移大幅度降低，主梁各控制点的竖向位移平均降低了26%以上；斜拉桥模型由2个辅助墩增加到4个后，主梁的竖向位移有所降低，但降低幅度相对较小，各控制点的竖向位移平均只降低了10%左右。

图11 主梁沿纵桥向的竖向峰值位移曲线图

Fig.11 Vertical peak displacement curve of the main beam along longitudinal direction of the bridge

表6 三种模型的主梁竖向峰值位移比

Tab.6 Ratios of vertical peak displacement of main beam between the three models

控制点位置/m位移比模型二/模型一模型三/模型二00.702 0.912700.738 0.8941330.732 0.9054000.588 0.904

为了分析辅助墩数量对支座竖向压力的影响，本文计算了三种模型在选取的8条地震动下各支座的最大压力与成桥支座压力比的均值(将支座反力的地震响应进行规则化),如表7所示。对于过渡墩P1处的支座最大压力，模型一在地震动下的最大压力均值达到17.53倍的成桥压力，随着过渡墩数量的增加，模型二和模型三P1墩的最大压力均值有所减小,相比于模型一，分别降低了15%和20%左右；对于辅助墩P2也出现类似的情况；但是对于T1主塔处的支座最大压力，则变化不大。

表7 三种模型的规则化支座竖向反力幅值

Tab.7 Regularized maximum bearing compression force of the three models

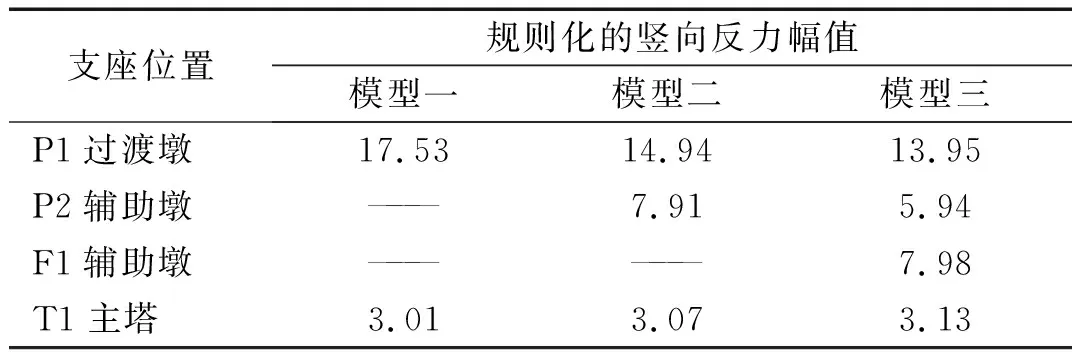
支座位置规则化的竖向反力幅值模型一模型二模型三P1过渡墩17.5314.9413.95P2辅助墩———7.915.94F1辅助墩——————7.98T1主塔3.013.073.13

由此可见，随着斜拉桥辅助墩个数的增加，过渡墩和辅助墩处的支座压力有所减小，但是相比于支座处的主梁竖向位移，支座压力的降低幅度相对较小，均在20%以内；对于T1主塔处的支座压力，由于主塔处的主梁竖向位移不大，主梁与支座产生的碰撞力也相对较小，辅助墩的增加对主塔处的支座压力几乎没有影响。

表8给出了三种模型在本文选取的8条地震动作用下主塔塔底最大弯矩和主梁梁端纵向峰值位移的均值。由表8可知，当辅助墩的数量由0个增加到2个，主塔塔底弯矩有所降低，最大弯矩均值降低了10%左右；当辅助墩由2个增加到4个，大部分地震作用下主塔塔底弯矩出现了增大的现象，主塔塔底弯矩均值由5 757 639 kN·m增加到5 809 518 kN·m，增大了1%左右。辅助墩的设置对于地震作用下的主塔内力而言，有两方面的作用：一方面增设辅助墩能够降低主梁传递到主塔上的水平地震惯性力，另一方面增设辅助墩提高了结构的整体刚度，增大主塔的地震响应，对主塔内力产生正反两方面效应，两者形成相互矛盾的关系。本文采用支座的初始刚度计算结构的动力特性，当辅助墩的数量由2个增加到4个，结构的纵向刚度提高，周期减小，结构的第一阶自振周期由 6.434 s降低到5.870 s，结构整体刚度的增大导致主塔塔底弯矩出现放大现象。随着辅助墩数量的增加，地震作用下主梁的纵向位移出现逐渐降低的趋势，从模型一到模型二再到模型三，主梁梁端的纵向峰值位移均值逐步降低7%左右，降低幅度相对较小。

表8 地震动作用下主塔塔底最大弯矩和粱端纵向峰值位移均值

Tab.8 The mean value of maximum bending moment at tower bottom and longitudinal peak displacement of main beam end under selected earthquakes

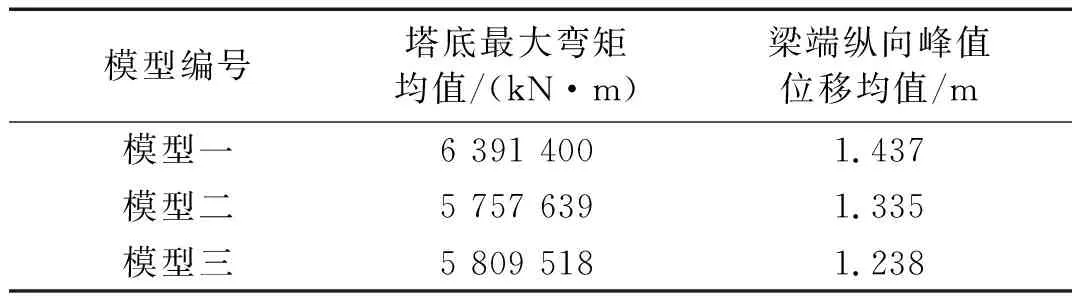
模型编号塔底最大弯矩均值/(kN·m)梁端纵向峰值位移均值/m模型一6 391 4001.437 模型二5 757 6391.335 模型三5 809 5181.238

由以上讨论可以得知，对于双塔斜拉桥，在边孔增设一辅助墩能够降低地震作用下脱空模型的主梁竖向位移及主梁与支座的竖向碰撞力，但是随着辅助墩数量的增加，支座竖向反力和主梁竖向位移变化幅度不大。

3.2 辅助墩成桥压力的影响

在常规的斜拉桥设计中，辅助墩处的成桥压力一般相对较大(背景工程中P2辅助墩处的成桥压力高达8 769 kN)，为了评估辅助墩成桥压力对支座脱空的影响，将背景工程(模型二)中过渡墩的成桥压力分别调整至5 500、6 500、7 500、8 500和9 500 kN，分别计算斜拉桥在NO.1地震动作用下的主梁竖向峰值位移和支座最大压力，分别如表9和表10所示。

表9 辅助墩成桥压力对主梁竖向峰值位移的影响

Tab.9 Influence of bearing compression force at finished state on maximum vertical displacement of the main beam

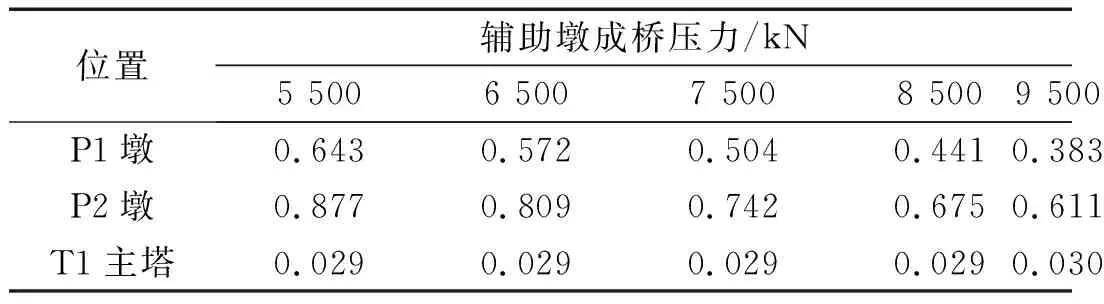
位置辅助墩成桥压力/kN5 5006 5007 5008 5009 500P1墩0.643 0.572 0.504 0.441 0.383 P2墩0.877 0.809 0.742 0.675 0.611 T1主塔0.029 0.029 0.029 0.029 0.030

由表9可以看出，随着辅助墩成桥压力的增大，P1墩和P2墩处的主梁竖向峰值位移呈现出逐渐减小的趋势，当辅助墩成桥压力由5 500 kN增加到9 500 kN，两处的主梁竖向峰值位移分别降低了40%和30%左右，降低幅度较大，由此可见，增加辅助的成桥压力可以显著地降低地震作用下支座脱空导致的较大主梁竖向位移；然而随着辅助墩成桥压力的改变，T1主塔处的主梁竖向峰值位移几乎没有变化，位移值也相对较低仅为0.03 m。

表10 辅助墩成桥压力对支座最大压力的影响

Tab.10 Influence of bearing compression force at finished state on maximum bearing compression force

位置辅助墩成桥压力/kN5 5006 5007 5008 5009 500P1墩26 612 25 282 24 175 23 003 23 616 P2墩55 902 56 313 55 676 54 483 52 873 T1主塔18 997 18 995 18 993 18 990 18 998

由表10可以看出，随着辅助墩成桥压力的增大，主梁的竖向位移得到了有效地控制，P1过渡墩处支座的最大压力逐渐减小，当辅助墩成桥压力由5 500 kN增加到9 500 kN，P1墩处支座的最大压力减小了11%左右；类似地，P2辅助墩处支座的最大压力总体上也呈现出逐渐减小的趋势，但降低幅度相对较小。对于P2辅助墩，增大成桥压力虽然能够显著地降低主梁的竖向位移，但是由于P2辅助墩处成桥压力的增大，所以有时会出现支座与主梁的碰撞力随成桥压力的增大而提高的现象，例如，当辅助墩的成桥压力由5 500 kN增加到6 500 kN时，P2墩处的支座最大压力由55 902 kN增加到56 313 kN，所以，在斜拉桥的设计中，辅助墩处的成桥压力需综合考虑结构的成桥状态以及抗震需求来加以确定。另外，随着辅助墩成桥压力的改变，T1主塔处支座的最大压力几乎没有变化，支座压力值也相对较低。

4 结 论

本文主要探讨了地震作用下斜拉桥的支座脱空现象，得到如下结论：

(1) 在设计地震作用下，背景工程多次在过渡墩、辅助墩和主塔处出现支座脱空现象。在支座脱空后，支座竖向压力大幅度增加。同时，支座处的梁体会产生较大的竖向位移。

(2) 支座脱空对辅助墩的影响明显大于过渡墩和主塔，相比于过渡墩和主塔，辅助墩处为支座受压的最不利位置。

(3) 支座脱空后，塔底弯矩和梁体纵向位移时程响应曲线偏离于不考虑支座脱空的结果，但支座脱空只是局部响应的变化，对梁体纵向位移和塔底弯矩等响应的影响较小。

(4) 对于双塔斜拉桥，在两侧边孔各增设一辅助墩能够降低地震作用下脱离模型的主梁竖向位移及主梁与支座的竖向碰撞力，但是随着辅助墩数量的持续增加，支座竖向反力和主梁竖向位移变化幅度不大。增设辅助墩虽然可以降低主梁梁端的纵向位移，但是由于其提高了结构的整体刚度，从而可能会导致主塔塔底弯矩出现放大现象。另外，增加过渡墩处成桥压力能显著地降低地震作用下脱离模型的主梁竖向峰值位移，同时在一定程度上降低支座的最大压力。而主塔处的支座压力和主梁竖向位移对辅助墩成桥压力的变化不敏感。